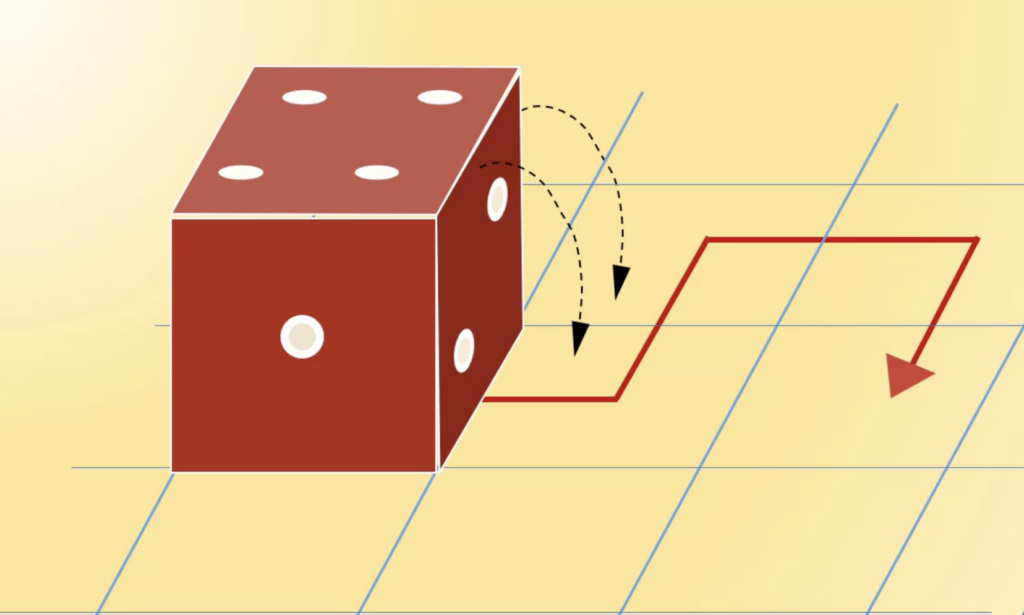
Есть классический игральный кубик и поле с нарисованным путём, который должен пройти этот кубик переворачиванием. Каждый шаг на этом поле — поворот кубика вдоль одной грани, чтобы он оказался на клетке с нарисованной траекторией.
Задача простая: понять, какая грань окажется наверху кубика в конце пути. Попробуйте решить эту задачу в уме, потому что на листочке она решается довольно просто.
 Логическая задача про часы, которую почему-то не могут решить старшеклассники
Логическая задача про часы, которую почему-то не могут решить старшеклассники Несложная задача на логику про три коробки и приз
Несложная задача на логику про три коробки и приз Самая неочевидная задача по математике, которую вы встречали
Самая неочевидная задача по математике, которую вы встречали Головоломная задача про соревнования на лошадях
Головоломная задача про соревнования на лошадях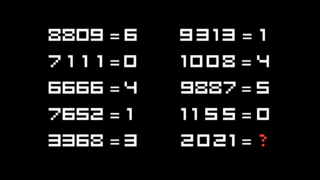 Задача на смекалку, которую невозможно решить обычными способами
Задача на смекалку, которую невозможно решить обычными способами Задача, где почти все врут, но нужно выяснить правду
Задача, где почти все врут, но нужно выяснить правдуПервое, что нам нужно вспомнить, — как распределяются грани в классическом игральном кубике. Правило там такое: сумма противоположных граней равна 7:
1 → 6
2 → 5
3 → 4
Зная это, составим пошаговое решение, переворот за переворотом. Решение будет без картинок, потому что с ними получается совсем просто. Включайте воображение!
Первое вращение (вправо):
Опрокинули на двойку → сверху пятёрка.
Спереди единица → сзади шестёрка (это не поменялось при вращении).
Четвёрка смотрит вправо.
Второе вращение (наверх):
Опрокинули на шестёрку → сверху единица.
Спереди появилась двойка (которая была внизу) → сзади шестёрка.
Четвёрка всё ещё смотрит вправо.
Третье вращение (вправо):
Опрокинули на четвёрку (которая смотрела вправо) → наверху тройка.
Двойка осталась спереди.
Остальное нам неважно.
Четвёртое вращение (вниз):
Опрокинули на двойку (которая была спереди) → сверху пятёрка.
Всё!
Получается, что при такой траектории пути и вращений наверху окажется пятёрка. Если смогли сделать это в уме — поздравляем, у вас шикарное воображение и классные логические способности!