Давно не было задачек! Вот подборка логических задач, которые ставят в тупик большинство взрослых, образованных людей.
Задача про хитрого электрика
Однажды в секретном кабинете что-то случилось с проводкой, и охрана вызвала электрика, чтобы он всё починил. Ему сказали, что три выключателя находятся снаружи, а три лампочки — внутри. Лампочки сейчас не горят. Каждый выключатель отвечает только за свою лампочку, но точной схемы не знает никто.
Электрику сказали как угодно щёлкать выключателями снаружи, но внутрь зайти разрешили только один раз. Внутри с лампочками тоже можно было делать что угодно, но по соображениям секретности возвращаться к выключателям уже нельзя. Электрик ухмыльнулся, пощёлкал выключателями, зашёл в комнату и сразу сказал, какой выключатель отвечает за каждую лампочку. Как он это сделал?
Если решать задачу в лоб, то сразу напрашивается такое решение: включить одну лампу и выключить другую. В итоге, когда мы зайдём в комнату, одна будет гореть, а другая — нет, и мы поймём, какой выключатель за что отвечает.
Но что делать с третьей лампой? Если мы включим и её, то как отличим от такой же первой? А если выключим, то как отличим от неработающей второй? Нужно научиться различать две одинаковые работающие или неработающие лампы.
Самый простой способ это сделать — разделить сами лампы дополнительно на тёплые и холодные. Лампа становится тёплой, когда поработает, и даже если её выключить, она всё равно какое-то время останется тёплой.
По условию мы знаем, что все три лампы выключены. Но вдруг они недавно включались и ещё не успели остыть? Значит, первое, что мы делаем, — ждём некоторое время, чтобы все лампы остыли.
Теперь щёлкаем любым выключателем и нагреваем одну лампу. После того, как она поработала достаточно времени, чтобы нагреться, мы её выключаем. Получается, что у нас все три лампы выключены, но две из них холодные, а одна — тёплая.
Затем, чтобы различить две холодные лампы, щёлкаем любым другим выключателем и заходим в комнату. В итоге мы увидим:
- одну работающую лампочку, которую мы включили только что;
- одну неработающую, но тёплую лампочку, которую мы нагрели до этого;
- и одну неработающую и холодную лампочку, выключатель от которой мы ни разу не трогали.
Тепло и логика!
Новые приключения хитрого электрика
Один провайдер решил провести интернет через реку — от левого берега до правого. Для этого он под водой проложил 49 проводов, по которым передаются сигналы и электрический ток.
Все провода оказались одинакового цвета, а подрядчик забыл промаркировать их, чтобы понять, где какие концы проводов на обоих берегах.
Чтобы выяснить, где что, позвали электрика и сказали ему подписать все провода числами от 1 до 49 с каждой стороны. Его задача — пронумеровать провода на левом берегу и на правом, разумеется, чтобы числа совпали.
Ему предоставили катер, который может возить его сколько угодно раз с одного берега на другой, линию с током на исходном берегу и мультиметр, который показывает напряжение в проводе.
Все думали, что электрик пересечёт реку как минимум 49 раз, но ему хватило всего двух раз — туда и обратно. Потом он просто сидел на берегу и задумчиво смотрел на воду. Как ему это удалось?
На исходном берегу электрик подаёт напряжение на любой провод и помечает его как № 1. Все остальные 48 он попарно соединяет между собой, чтобы на этой стороне получился один провод под напряжением и 24 пары. Как он это делает — вообще не важно, порядок пар сейчас роли не играет. После этого электрик отправляется на правый берег (первая поездка).
Приплыв на место, он находит провод под напряжением с помощью тестера — это провод № 1, он его так и помечает. А дальше начинается электрическая магия.
Электрик берёт провод № 1 под напряжением, соединяет его с любым другим проводом и подписывает его как № 2. Но мы помним, что на левом берегу все провода соединены попарно, значит, провод № 2 с той стороны тоже с чем-то соединён, а значит, ток вернётся обратно и появится в новом проводе, который электрик подпишет как № 3.
Дальше всё то же самое: он берёт провод с током № 3, соединяет его с любым оставшимся проводом и подписывает новый провод как № 4. А ещё он помнит про пары на том берегу, поэтому ищет провод, в котором снова появился ток, и подписывает его как № 5. Таким же образом он соединяет оставшиеся провода и нумерует все жилы на правой стороне от 1 до 49. Сделав это, электрик возвращается на левый берег (вторая поездка).
Осталось самое интересное: как на этом берегу проставить те же самые числа на проводах. Электрик знает, как выглядит провод № 1, потому что он его подписал, но не знает, как выглядит провод № 2.
Но он помнит, что провод № 1 соединён на том берегу с проводом № 2, который на этом берегу соединён с проводом № 3. Значит, задача электрика в том, чтобы найти это соединение на левом берегу, где он находится. Для этого он разъединяет по очереди все соединения и смотрит, пропал ли ток во всех остальных проводах. Если не пропал во всех остальных — значит, разъединил не ту пару и возвращает её на место. А если пропал — значит, электрик нашёл соединение проводов № 2 и № 3. При этом тот неизвестный провод, который остался под напряжением, будет провод № 2, а тот, с которым он соединялся, будет № 3.
После этого электрик соединяет подписанную пару обратно и начинает искать следующую точку, которая отключает все остальные жилы — это будут провода № 4 и № 5. Действуя по этой схеме, хитрый электрик подпишет все оставшиеся провода. Провайдеру останется только разъединить пары на каждом берегу.
Как перевезти гопников и философов с одного берега на другой
На одном берегу реки находятся шесть человек: три гопника и три философа. Пока что они ведут непринуждённые беседы об экзистенциальном, но все должны будут рано или поздно оказаться на другом берегу.
Есть одна лодка, в которую могут поместиться только два человека, но философы управлять лодкой не умеют, а гопники умеют. Также нельзя оставлять на одном берегу философов больше, чем гопников, потому что тогда философы взорвут мозг гопникам разговорами о природе вещей. Как переправить всех через реку?
Для первой поездки есть четыре варианта:
- один гопник — не подходит, потому что на берегу философов становится больше и они взорвут мозг;
- два гопника — не подходит по той же причине;
- один или два философа — тоже нет, потому что они не умеют управлять лодкой;
- философ и гопник — единственный вариант, который остаётся.
Значит, первым рейсом пара «философ-гопник» отправляется на другой берег:
Теперь лодку надо как-то отправить назад. Но так как философ не умеет ей управлять, то он остаётся на берегу, а гопник — возвращается. Философы не взрывают никому мозг:
Теперь прикинем варианты следующего рейса. Мы не можем отправить двух гопников, иначе философы останутся в большинстве, и настанет на левом берегу полный экзистенциализм.
Поэтому снова на тот берег уплывают философ с гопником. Причём гопник высаживает философа, но сам из лодки не вылезает — если так не сделать, то он останется с двумя философами на том берегу и они увлекут разговорами об идеях вещей:
Таким образом, у нас на том берегу сидят два философа, а на этом — один философ и три гопника, на которых он вряд ли сможет воздействовать силой дискурса:
Теперь нам нужно сделать выбор, кто поедет на этот раз. Можно отправить снова философа и гопника, но тогда на том берегу окажутся три философа. И безопасно перевезти остальных гопников поодиночке уже не получится — философы всегда будут в большинстве.
Значит, остаётся только один вариант: отправить в путь двух гопников. В итоге на том берегу всех будет поровну и всё пройдёт спокойно:
Но лодку надо как-то отправить на другой берег. Нельзя разместить на ней одного гопника, потому что второй останется в меньшинстве среди философов. Двум гопникам ехать обратно тоже не вариант, потому что они только что прибыли.
Поэтому назад отправляются философ и гопник:
Теперь единственный безопасный вариант — отправить на тот берег двух гопников:
Назад отправим одного гопника. Чтобы не выходить из лодки, он позовёт в неё философа (например, фразой «Что вы думаете о солипсизме?») и вернётся с ним обратно на тот берег:
Точно так же забираем оставшегося философа:
И в итоге вся компания оказывается на том берегу, бездонное небо — над головой, а нравственный закон — внутри:
Как рассадить интровертов в баре
А вот задачка на структуры данных, сортировку и алгоритмику, которая возможна только в нашей стране.
В Петербурге на улице Рубинштейна есть один бар, в который ходят лишь необщительные люди, назовём их интровертами. (На самом деле интроверты общительные, необщительность — это миф. Но это задачка, поэтому упростим.)
Интроверты садятся вдоль барной стойки, где есть 25 мест. Когда входит новый посетитель, он всегда садится у стойки как можно дальше от остальных гостей. Никто не садится на соседнее место рядом с другим интровертом: если кто-то входит и видит, что свободных мест мало и надо сесть рядом с кем-то, то он уходит.
Бармен хочет получить как можно больше клиентов. У него есть право посадить самого первого посетителя на любое место у стойки. Куда выгоднее посадить первого интроверта с точки зрения бармена?
Для начала найдём идеальный вариант, который устроил бы бармена. Для этого нарисуем 25 квадратов в ряд и закрасим те, на которых кто-то сидит. Помните, что ни один интроверт по задаче не сядет на соседнее место к другому.
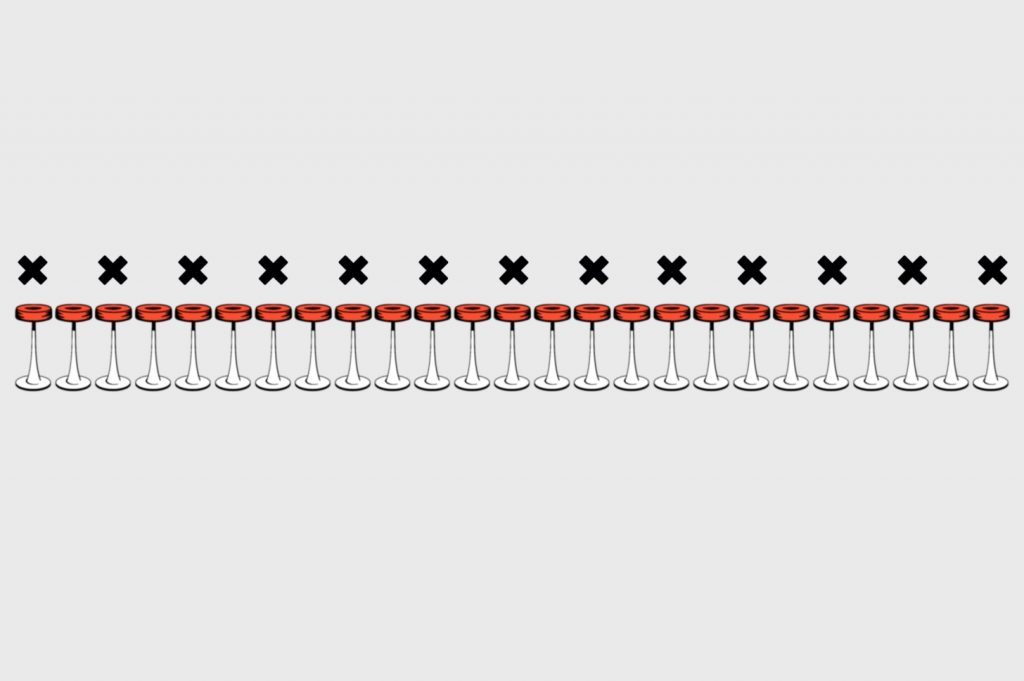
Получается, что это самая плотная рассадка, которая возможна в этом баре. Так у стойки сидят 13 человек. Осталось только найти место для самого первого посетителя.
Для начала попробуем решить эту задачу в лоб и посадим первого посетителя на первый стул:
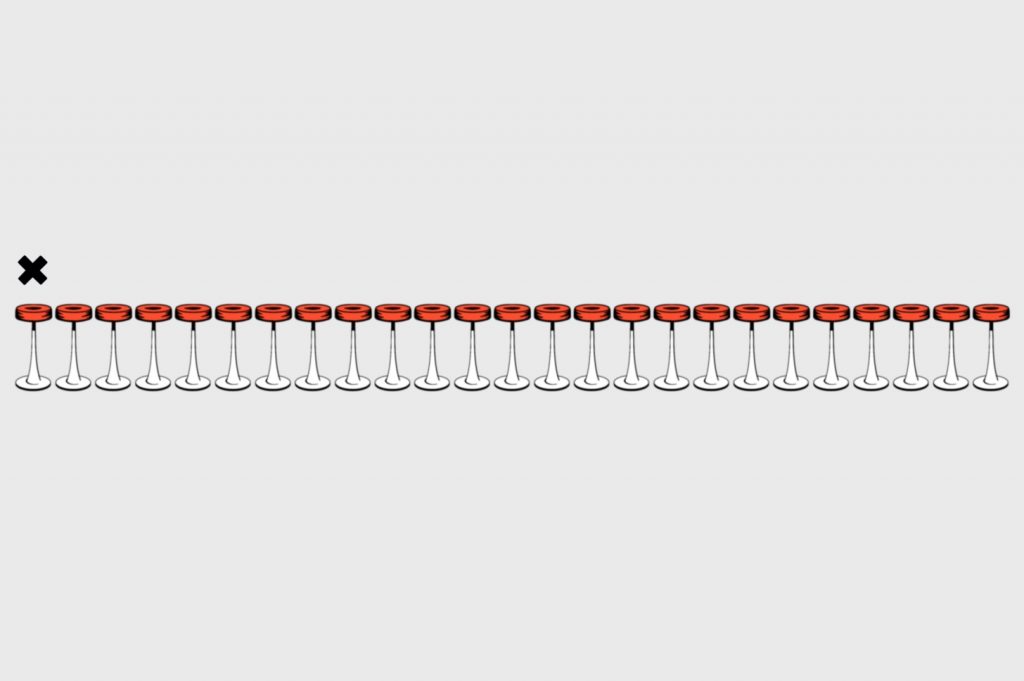
Теперь второй посетитель должен сесть на свободное место как можно дальше от него, то есть занять стул № 25:
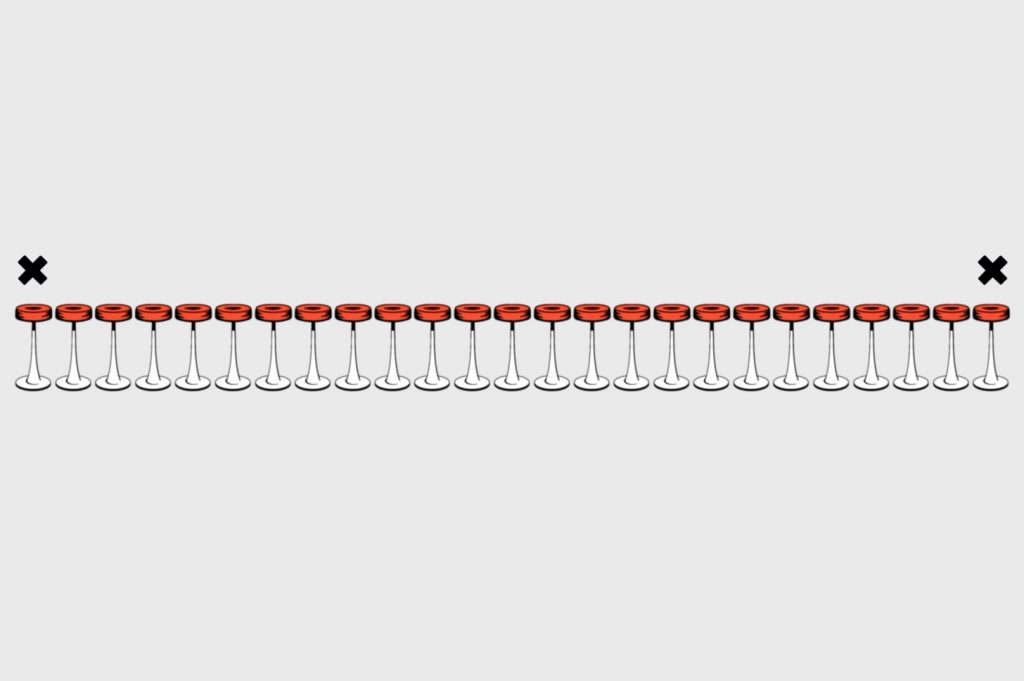
Третьему достаётся стул № 13, так как он ровно посередине между этими двумя:
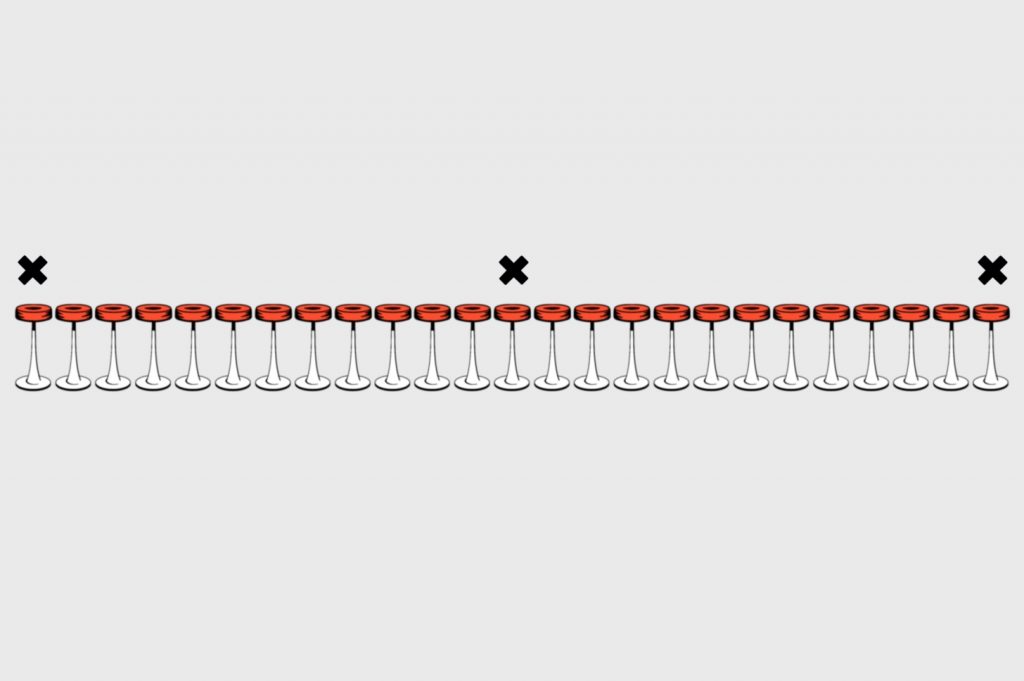
Два следующих займут свободные места точно посередине между центральным и боковыми:
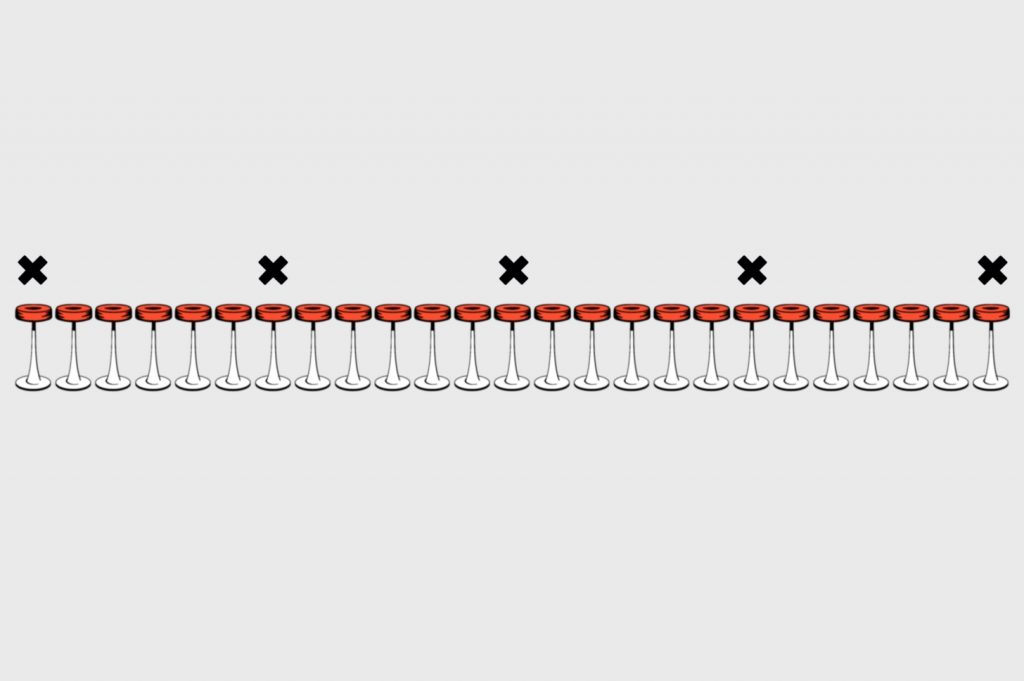
И вот тут настаёт момент истины: четыре следующих посетителя тоже сядут точно посередине между занятыми местами. Это значит, что между каждым будет по 2 пустых места:
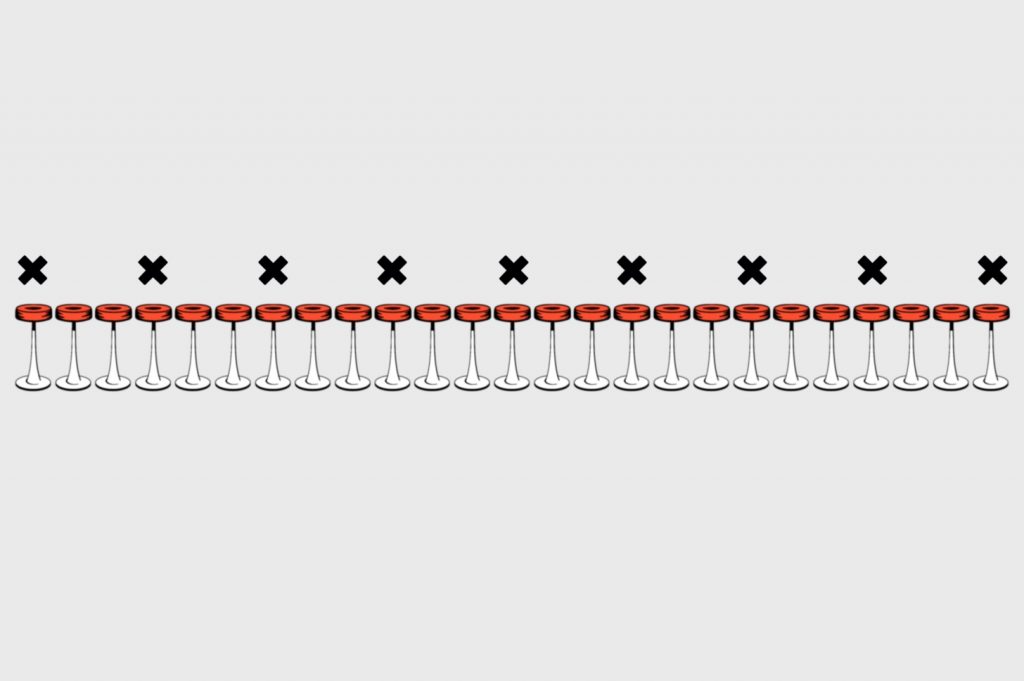
В итоге у нас занято всего 9 мест, но сесть больше никуда нельзя: у каждого свободного стула есть как минимум один занятый сосед. Значит, этот вариант не подходит. Нужен другой.
Чтобы прийти к правильному ответу, попробуем решать задачу с конца.
Вспомним идеальную рассадку:
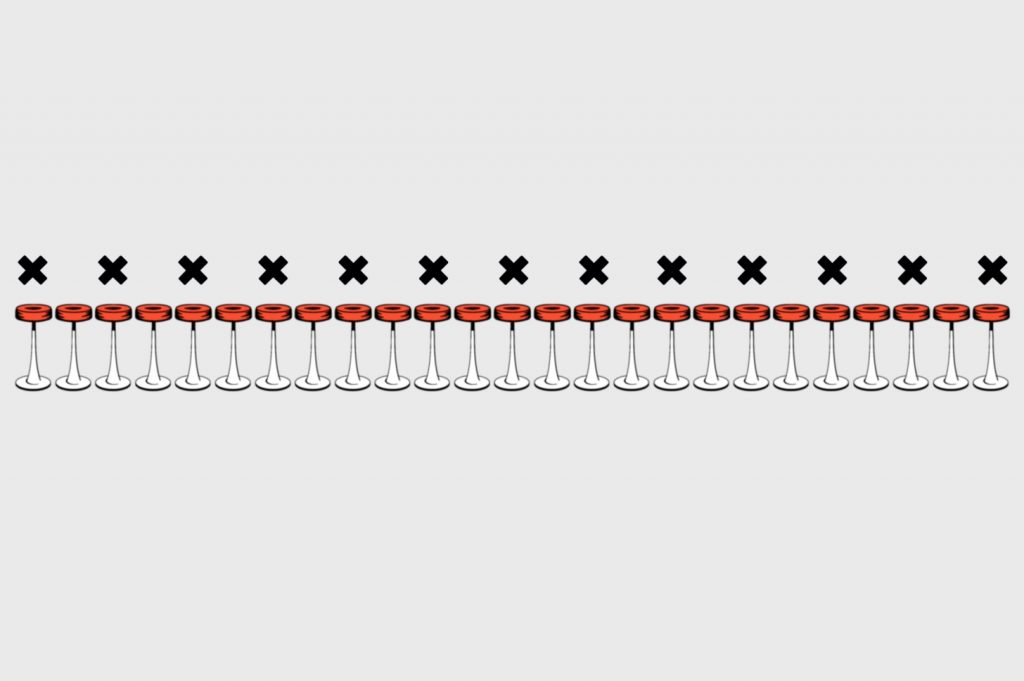
Здесь сидит максимальное количество гостей — 13, и между каждым из них есть свободное место. Отмотаем на шаг назад и посмотрим, как могли бы сидеть интроверты, чтобы новые гости сели точно между ними:
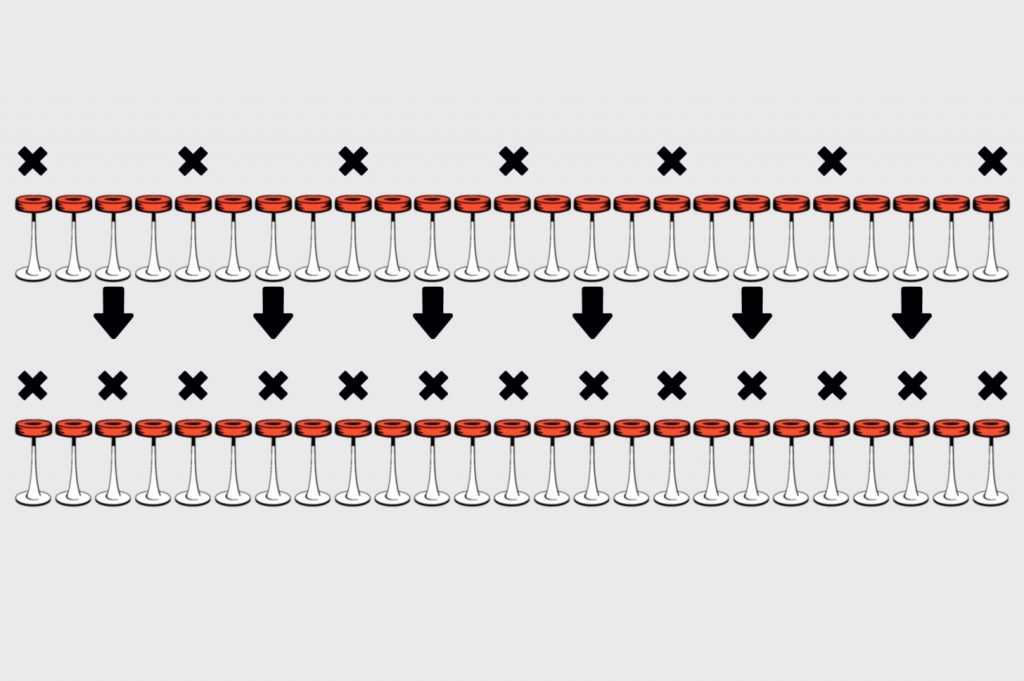
В этом случае 6 новых гостей садятся точно посередине между занятыми стульями и идеально заполняют все места.
Теперь сделаем ещё шаг назад и посмотрим, как должны сидеть гости, чтобы новые клиенты сели на нужные стулья:
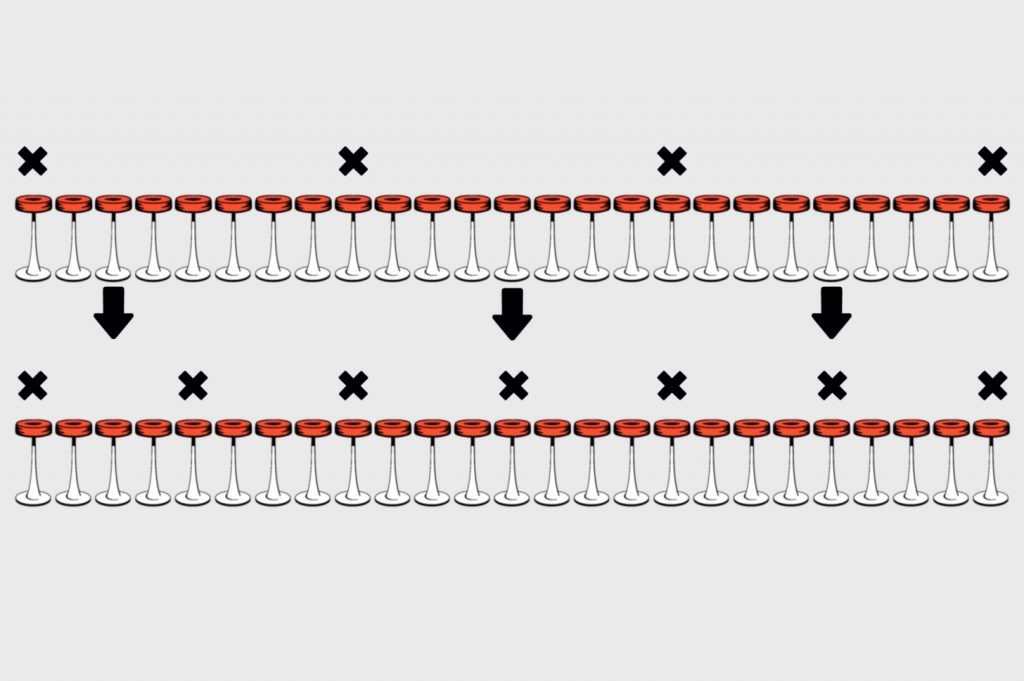
Получается, что если мы посадим первых четырёх гостей так, как на рисунке выше, то дальше всё будет хорошо. Сделаем ещё шаг назад, чтобы понять, как они смогли так сесть:
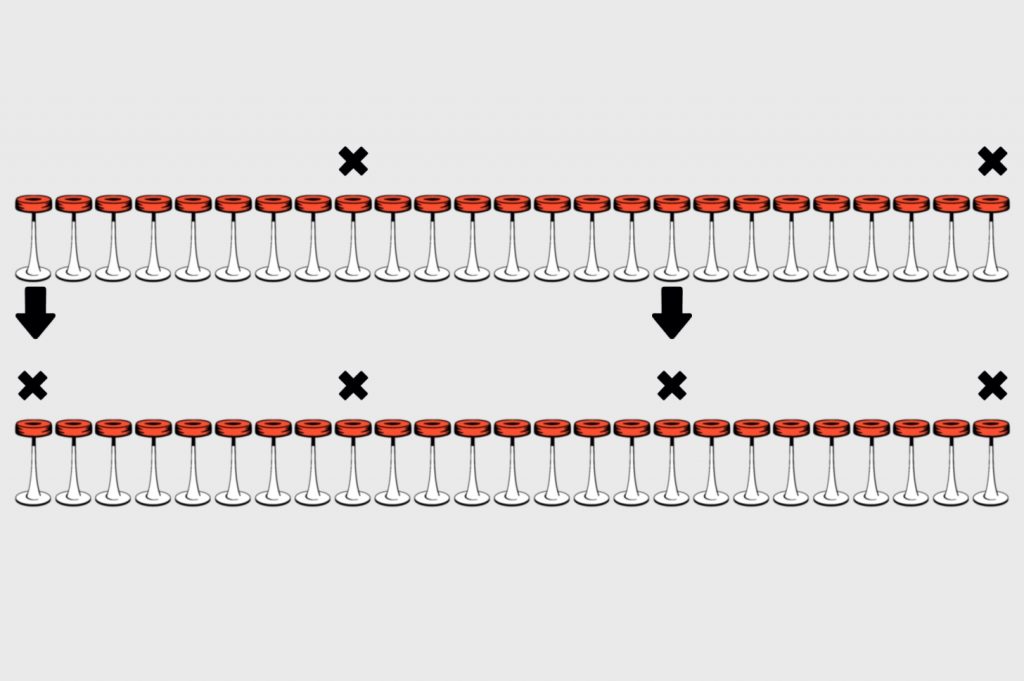
Из рисунка видно, что два новых посетителя должны сесть как можно дальше от занятых мест. Для этого один садится ровно посередине между двумя занятыми, а второй — с самого края, на первое место. Таким образом, между всеми ними будет максимально возможное расстояние. Осталось понять, как сели эти первые два интроверта.
Если бы первый гость сел с краю на стул № 25, второму бы пришлось сесть с противоположного края на стул № 1 (мы это разобрали в самом начале, в неправильном варианте). Значит, первый гость сел на стул № 9, а второму пришлось сесть максимально далеко от него — на самый последний стул:
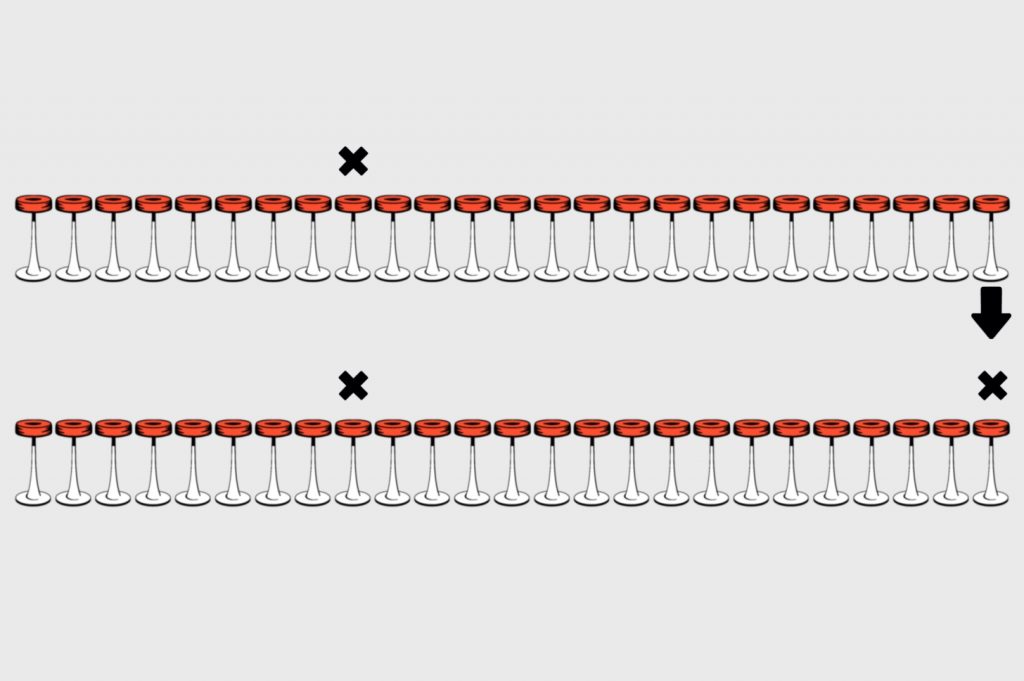
Получается, самого первого гостя бармен должен посадить на стул № 9.
Как так вышло? Просто посчитали от обратного. Программисты называют это Test-First Development, хех.
Логическая задача про лифт
Однажды в 20-этажном доме вандалы-математики разбили почти все кнопки в лифте, сохранив только две. От короткого замыкания последние стали работать так: одна поднимает лифт на 13 этажей, а вторая опускает на 8.
Как жильцам попасть с 13-го этажа на 8-й?
В этой задаче есть момент из реальной жизни, который существенно упрощает решение. Но начнём с классического ответа.
Суть в том, что лифт не может выезжать за границы этажей. То есть если на 13 этаже мы нажмём кнопку «вверх», которая должна поднять лифт на 13 этажей, то он никуда не поедет, потому что 13 + 13 = 26, а в доме столько этажей нет. Значит, единственное, что нам остаётся на первом шаге — нажать «вниз»:
Вниз → 5 (13 - 8).
Здесь 5 — это номер этажа, на который приехал лифт, а цифры в скобках показывают начальный.
С 5 этажа мы можем уехать только вверх. Получается, что каждый раз у нас есть только один вариант, на какую кнопку нажимать. Давайте попробуем применить этот принцип и посмотреть, что получится:
Вниз → 5 (13 - 8).
Вверх → 18 (5 + 13).
Вниз → 10 (18 - 8).
Вниз → 2 (10 - 8).
Вверх → 15 (2 + 13).
Вниз → 7 (15 - 8).
Вверх → 20 (7 + 13).
Вниз → 12 (20 - 8).
Вниз → 4 (12 - 8).
Вверх → 17 (4 + 13).
Вниз → 9 (17 - 8).
Вниз → 1 (9 - 8).
Вверх → 14 (1 + 13).
Вниз → 6 (14 - 8).
Вверх → 19 (6 + 13).
Вниз → 11 (19 - 8).
Вниз → 3 (11 - 8).
Вверх → 16 (3 + 13).
Вниз → 8 (16 - 8).
В итоге за 19 поездок мы добрались до нужного этажа. Самое интересное, что по этим правилам лифт дальше никуда поехать не может: 8 + 13 = 21, а 8 - 8 = 0, что выходит за границы этажей. Придётся всё-таки вызывать мастера и делать ремонт.
Но есть и второе решение. Чаще всего в жизни бывает так: как только лифт доезжает до самого верхнего или нижнего этажа, он останавливается, независимо от того, сколько ещё ему оставалось проехать. Это логично: дошли до граничных значений и остановились. Воспользуемся этим и попробуем решить нашу задачу быстрее:
Вниз→ 5 (13 - 8).
Вниз → 1 (5 - 8) → доехали до первого этажа и остановились.
А как добраться с 1 этажа на 13 мы уже знаем из прошлого решения:
Вверх → 14 (1 + 13).
Вниз → 6 (14 - 8).
Вверх → 19 (6 + 13).
Вниз → 11 (19 - 8).
Вниз → 3 (11 - 8).
Вверх → 16 (3 + 13).
Вниз → 8 (16 - 8).
Итого 9 поездок. В два раза меньше, чем первым способом!
Граждане, берегите лифт!
Находчивый инженер в кафе
В кафе поставили 3 разных автомата, которые наливают напитки. В первом – кофе, во втором – чай, а в третий выдаёт случайным образом то кофе, то чай (потому что в жизни всегда должно быть место эксперименту). Для каждого из автоматов нужна 1 монета, чтобы получить напиток.
На заводе перепутали маркировку автоматов, поэтому на каждом из них оказалась неправильная наклейка. Сколько монет понадобится находчивому инженеру, чтобы понять, где какой автомат?
Несмотря на то что задача кажется запутанной, у неё довольно изящное решение. Следите за руками находчивого инженера.
Кидаем монету в автомат с наклейкой «Чай-кофе». Мы знаем, что на нём неправильная наклейка, как и на всех, поэтому правильная будет либо «Чай», либо «Кофе». Теперь смотрим, что нам выдаст этот автомат.
Например, он выдал чай. Значит, правильная наклейка для этого автомата — «Чай». Теперь нам нужно найти кофейный автомат среди двух оставшихся.
Мы помним, что все наклейки перепутаны, поэтому там, где будет написано «Кофе», на самом деле не кофейный автомат. Чай тоже уже занят. Поэтому под надписью «Кофе» скрывается автомат, который выдаёт и кофе, и чай.
Значит, с наклейкой «Чай» будет автомат, который выдаёт кофе.
О чудо! Чтобы разобраться с наклейками, достаточно всего одной монеты!
Как успеть на презентацию
Илон Маск, Билл Гейтс, Тим Кук и Марк Цукерберг хотят первыми попасть на презентацию Xiaomi, поэтому решили выйти ночью, чтобы к утру быть уже на месте. Кругом темнота, без фонарика никому идти нельзя, но он один на всех. Презентация — на другом берегу великой реки Янцзы. Мост через реку хлипкий и может выдержать одновременно максимум двоих. Как всем перебраться на другой берег как можно скорее?
Скорость перехода моста у каждого своя: проворный Илон Маск переходит его за 1 минуту, бодрящийся Билл Гейтс — за 2, спокойный Тим Кук — за 5. Марк Цукерберг после слушаний в Конгрессе быстро ходить не может, поэтому тратит на мост 10 минут. Когда мост переходят два человека, их скорость равна скорости самого медленного из пары.
Задача — перевести героев на другой берег как можно скорее, ведь места в очереди у конгресс-центра уже занимают местные жители.
Самая скоростная пара у нас — Маск и Гейтс, поэтому они с фонариком переходят на другой берег за 2 минуты (скорость Гейтса):
Илон Маск (1) и Билл Гейтс (2) → перешли на тот берег за 2 минуты.
Отправляем с фонарём назад самого быстрого из них:
Илон Маск (1) → вернулся обратно с фонарём за 1 минуту.
Теперь нужно решить, какая пара пойдёт следующей. Так как нам в любом случае нужно отправлять Цукерберга на тот берег, то это гарантированно займёт долгих 10 минут. Чтобы использовать это время оптимально, отправим с ним Тима Кука, который тоже не самый быстрый из всех:
Тим Кук (5) и Марк Цукерберг (10) → перешли на тот берег за 10 минут.
Осталось забрать Илона Маска с того берега, значит посылаем за ним самого быстрого из доступных — Билла Гейтса:
Билл Гейтс (2) → вернулся обратно с фонарём за 2 минуты.
И они вдвоём с Маском отправляются на тот берег:
Илон Маск (1) и Билл Гейтс (2) → перешли на тот берег за 2 минуты.
Складываем все минуты на мосту: 2 + 1 + 10 + 2 + 2 = 17 минут. Значит, всего 17 минут им потребуется, чтобы перейти великую реку Янцзы и занять места в зале раньше всех.
Находчивый альпинист
Один альпинист неудачно спустился с горы и наступил сразу на двух змей — кобру и гадюку. Одна из них его укусила, какая — неизвестно. У него были с собой противоядия, по две таблетки каждого вида: против кобры и против гадюки. Одну таблетку нужно принять сразу после укуса, а другую — на следующий день.
Альпинист вытряхнул из упаковки на ладонь одну таблетку от кобры (K), стал вытряхивать таблетку от гадюки (Г), но рука дрогнула и из упаковки Г выпали обе таблетки. Теперь у него в руке три абсолютно одинаковые таблетки: одна K, две Г. А ему нужно немедленно принять одну K и одну Г, оставив по второй таблетке каждого противоядия на завтра. Что ему делать?
Если таблетки никак нельзя отличить друг от друга, значит, надо придумать такое решение, которое не потребует анализа всех таблеток.
Задача альпиниста — принять одну таблетку от укуса кобры и одну от укуса гадюки. На ладони лежат три таблетки, и если мы возьмём любые две, то есть вероятность, что нам попадутся две таблетки от гадюки и тогда противоядие от кобры не сработает (альпинист же не знает, какая именно змея его укусила). Значит, нам такой вариант не подходит.
Чтобы сегодня и завтра принять одинаковые порции, альпинисту нужно к этим трём таблеткам добавить четвёртую, разломать их все пополам и разнести эти половинки по двум разным кучкам. Смысл в том, чтобы в каждой кучке лежало по одной половинке от каждой таблетки. Тогда в обеих будет по две половинки таблетки от кобры и по две половинки таблетки от гадюки, а две половины дают как раз целую таблетку.
Получается, что ему сегодня и завтра нужно съесть по 4 половинки, по одной от каждой таблетки.