Безумная задача про лапшу из собеседования, которую можно решить без сложной математики

Обычно на собеседованиях предполагается, что мы подумаем и найдём эдакое изящное и красивое решение, которое поразит рекрутера и выставит нас в выгодном свете.

Но не в этот раз.

Эту задачу можно решить как математик (и этого от нас как бы и ждут), но выкладки не понравятся ни нам, ни вам:

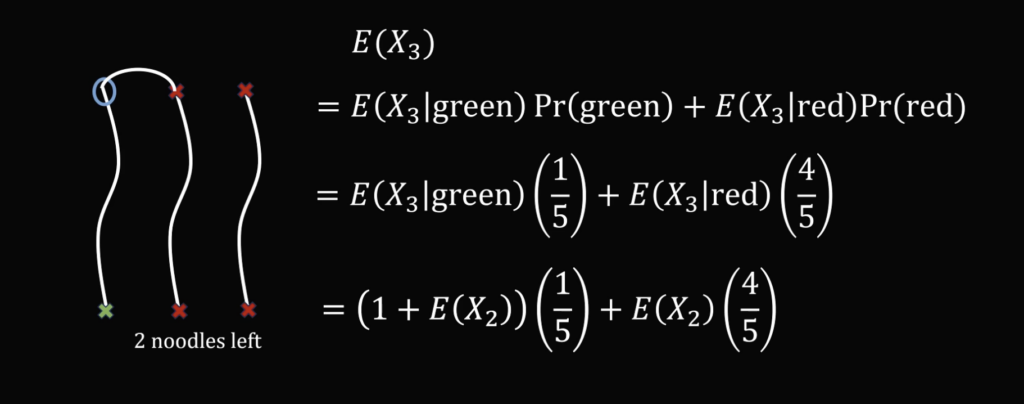
↑ И это только для трёх лапшинок. С сотней там начинается вообще абстрактная жесть.

Поэтому пойдём на хитрость, как настоящие айтишники: мы напишем несложный код, который будет имитировать действия по ходу задачи, а мы посмотрим на финальный результат.

Вместо сложной математики напишем код, который будет моделировать процесс, где у нас есть 100 лапшинок, каждая с двумя концами. Повтори эксперимент 10 000 раз, чтобы получить статистически точные результаты. В начале каждого эксперимента все лапшинки разделены, поэтому вначале создадим список всех свободных концов (200 штук), которые нужно будет соединять.

После этого случайным образом выбираем два свободных конца и соединяем их. Если это концы одной лапшинки — получаем петлю и увеличиваем счётчик петель. Если концы принадлежат разным лапшинкам — они объединяются в одну более длинную лапшинку. Процесс продолжается, пока не останется свободных концов. В результате все лапшинки соединяются в некоторое количество петель разного размера.

После каждого эксперимента программа записывает, сколько всего петель получилось. Если все лапшинки соединились в одну большую петлю — это особый случай, который отмечается отдельно.

В итоге без математического аппарата чисто на знании программирования мы найдём ответ — достаточно точный, чтобы считаться правильным. Если нужна большая точность, поставьте не 10 тысяч, а 10 миллионов симуляций и оставьте компьютер минут на 10–20, пусть поработает.

Как обычно, прокомментировали каждую строчку кода, чтобы было понятно, что происходит на каждом этапе. Ответ специально не пишем — найдите его сами :-)

# подключаем модуль для работы со случайными числами
import random

# и библиотеку для математических вычислений для расчёта среднего значения
import numpy as np

# определяем функцию для симуляции процесса соединения лапшинок
# n_noodles — количество лапшинок, n_simulations — количество повторений эксперимента
def correct_noodle_simulation(n_noodles=100, n_simulations=1000):

    # создаём пустой список для записи количества петель в каждом эксперименте
    loops_counts = []
    
    # счётчик для подсчёта случаев, когда все лапшинки соединились в одну большую петлю
    one_big_loop_count = 0
    
    # начинаем цикл по количеству симуляций (экспериментов)
    for sim in range(n_simulations):
        # изначально каждая лапшинка — отдельная компонента, а мы представляем каждую лапшинку как множество её концов
        # теперь создаём список множеств, где каждое множество содержит номер одной лапшинки
        noodles = [set([i]) for i in range(1, n_noodles + 1)]
        
        # свободные концы: изначально у каждой лапшинки 2 свободных конца, поэтому создаём пустой список для хранения всех свободных концов
        free_ends = []
        
        # заполняем список свободных концов — для каждой лапшинки добавляем два одинаковых номера
        for i in range(1, n_noodles + 1):
            free_ends.extend([i, i])
        
        # процесс случайного соединения концов — продолжаем, пока есть хотя бы два свободных конца для соединения
        while len(free_ends) >= 2:
            # для этого выбираем два случайных разных конца из списка свободных концов
            end1, end2 = random.sample(free_ends, 2)

            # заводим переменные для хранения индексов найденных лапшинок
            noodle1_idx = None
            noodle2_idx = None          

            # теперь находим лапшинки, которым принадлежат эти концы
            # для этого проходим по всем лапшинкам, чтобы найти, каким лапшинкам принадлежат выбранные концы
            for i, noodle in enumerate(noodles):
                # проверяем, принадлежит ли первый конец текущей лапшинке
                if end1 in noodle:
                    noodle1_idx = i
                # а затем поверяем, принадлежит ли второй конец текущей лапшинке
                if end2 in noodle:
                    noodle2_idx = i
            
            # после этого удаляем использованные концы из списка свободных концов лапшинок
            free_ends.remove(end1)
            free_ends.remove(end2)
            
            # проверяем, принадлежат ли выбранные концы одной и той же лапшинке
            if noodle1_idx == noodle2_idx:
                # если это одна и та же лапшинка — получается петля, и мы просто удаляем концы из исходного массива
                pass
            else:
                # если это разные лапшинки
                # объединяем их — создаём одну большую лапшинку из двух
                noodles[noodle1_idx] = noodles[noodle1_idx].union(noodles[noodle2_idx])
                # и удаляем вторую лапшинку из списка, так как она объединилась с первой
                noodles.pop(noodle2_idx)
        
        # подсчитываем, сколько отдельных лапшинок/петель осталось
        loops = len(noodles)
        # и добавляем результат текущей симуляции в общий список
        loops_counts.append(loops)
        
        # наконец, проверяем, образовалась ли одна большая петля из всех лапшинок
        if loops == 1:
            # и увеличиваем счётчик больших петель
            one_big_loop_count += 1
    
    # вычисляем среднее количество петель по всем симуляциям
    average_loops = np.mean(loops_counts)
    # и также считаем вероятность образования одной большой петли
    prob_one_big_loop = one_big_loop_count / n_simulations
    
    # возвращаем результаты вычислений
    return average_loops, prob_one_big_loop

# запускаем программу
print("🔬 Наливаем лапшичный суп в тарелку и запускаем симуляцию...")

# для этого вызываем функцию симуляции с параметрами: 100 лапшинок, 10000 экспериментов
avg_loops, prob_big_loop = correct_noodle_simulation(n_noodles=100, n_simulations=10000)

# выводим среднее количество петель
print(f"🍜 Среднее количество петель из {100} лапшинок: {avg_loops:.4f}")

# и вероятность образования одной большой петли
print(f"🎯 Вероятность одной большой петли: {prob_big_loop:.6f}")