Можно ли создать автоматическую счётную машину, если у вас есть только бусины и палки? Да, можно.
На наш друг Эван из YouTube провёл такой опыт и получил интересный результат: он создал механическую счётную машину, которая работает как обычный цифровой калькулятор, но при этом не требуют ни электричества, ни микрочипов. Всё работает благодаря гравитации и двоичной логике.
Если вы понимаете по-английски, смотрите видео. Если нет — читайте наш разбор.
В чём идея
Существуют электронные калькуляторы: они используют алгоритмы преобразования двоичного кода, чтобы складывать, умножать, вычитать и делить.
Все алгоритмы основаны на логических операциях: И, ИЛИ, НЕ и др. Если взять два числа в двоичном коде и прогнать каждый их бит через последовательность логических операций, то на выходе получится, например, сумма. Соль в том, чтобы правильно соединить между собой логические операции.
В обычной жизни логические операции исполняют транзисторные полупроводники. Представьте, что это трубы и краны, только не для воды, а для электричества. И электричество, которое «вытекает» из одного крана, может управлять открытием или закрытием другого крана.
Если много-много раз правильным образом соединить эти полупроводниковые «краны», получится калькулятор.
Что новенького
Эван решил сделать калькулятор на той же логической базе, что и настоящие калькуляторы, но с одним отличием: вместо тока и полупроводников он использует бусины и силу гравитации. Бусинки падают вниз, катятся, задевают какие-то стены, отодвигают что-то на своём пути и так далее. При этом такой калькулятор работает как нужно: числа считаются и все логически элементы работают правильно.
🤔 Зачем это нужно? Да просто так.
Двоичная логика
Самые простые состояния в логике — ДА и НЕТ. Их два, поэтому такая логика, где используются только два состояния, называется двоичной. Мы уже разбирали, как устроена двоичная логика и почему она используется для всех вычислений в компьютере.
В транзисторах ДА обозначается единицей и наличием тока в проводнике, а НЕТ — нулём и отсутствием тока. Так как у нас вместо тока бусинки, то правила будут такие:
1 = есть бусинка
0 = нет бусинки
Этого нам хватит, чтобы сделать логические элементы. Чтобы работать с числами, мы просто будем переводить их в двоичную систему счисления и смотреть, в каком порядке ставить бусинки и пустоту между ними.
Например, вот как в двоичном представлении будет выглядеть число 5:
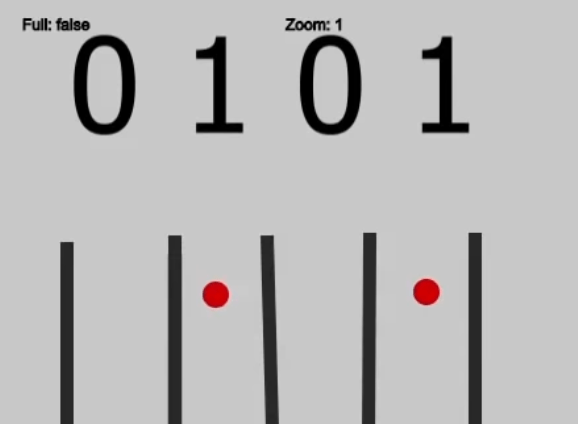
А вот как запишется число 12:
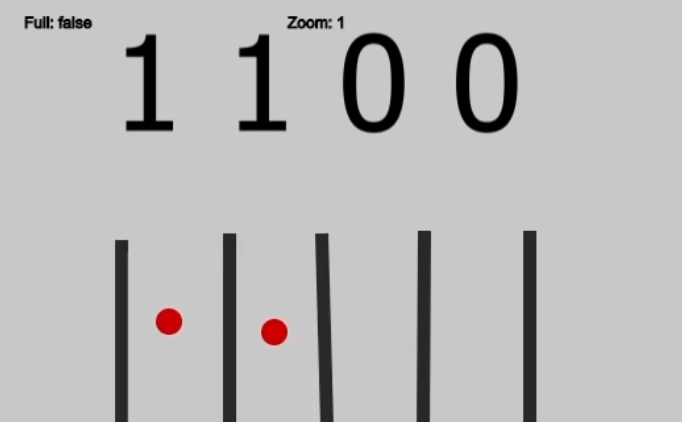
🤔 Если не понимаете, почему цифры стоят именно в этих местах, — прочитайте статью про двоичное счисление, там всё хорошо объяснено.
Логическое И
Первое, что делаем, — реализуем логическое И. Если забыли, что это такое, — почитайте в статье про транзисторы, а пока вот короткая справка:
На вход поступает два сигнала. Логическое И выдаёт в результате единицу, только если на вход поступило сразу две единицы. Если хотя бы один из них ноль — будет ноль.
Так как у нас бусинки, то на входе и выходе тоже будут бусинки. Первая версия элемента, которую сделал Эван, выглядела так:

Логика была такая: падают две бусинки, одна закрывает ямку, вторая перекатывается и передаёт сигнал дальше. Если бусинка будет одна, то она застрянет в лунке и сигнал дальше не пойдёт.
Но такая реализация оказалась ненадёжной:

Эван модернизировал элемент, добавив в него розовые подвижные части — в зависимости от положения бусинок они сдвигались, освобождая итоговую бусинку:
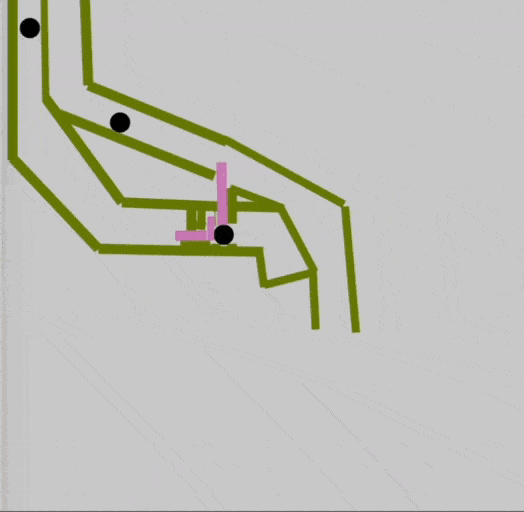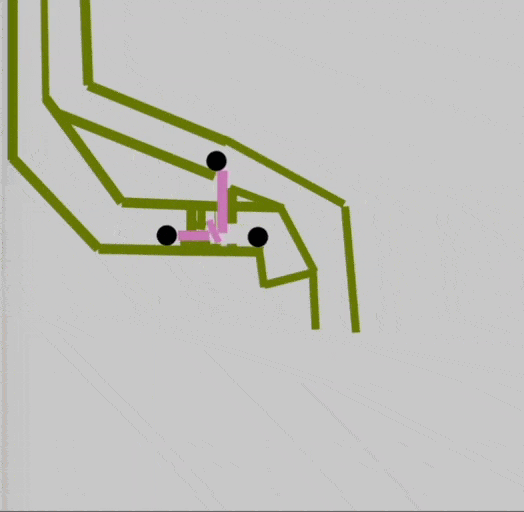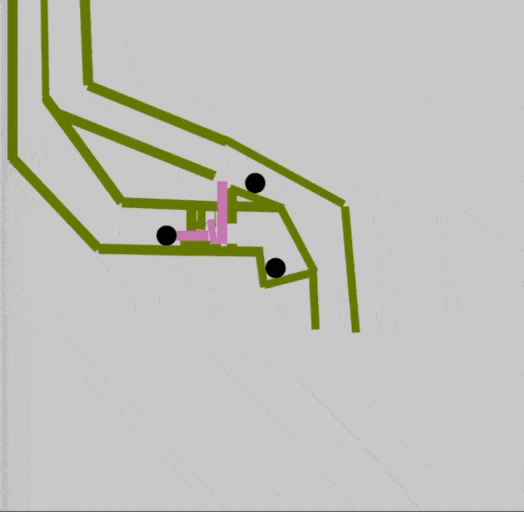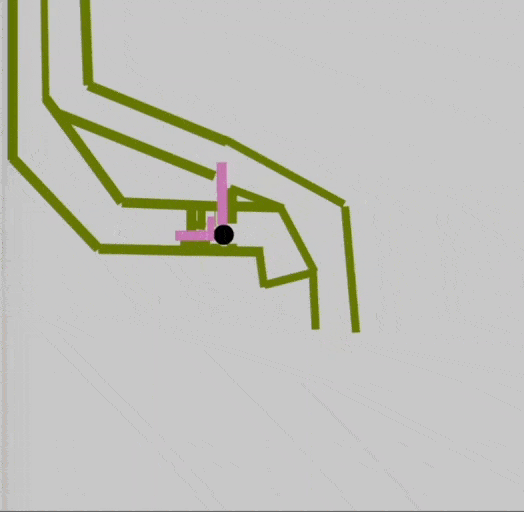
Отлично, попробуем так же реализовать остальные элементы.
Логическое ИЛИ
ИЛИ отличается от И тем, что на входе достаточно хотя бы одной единицы, чтобы на выходе тоже получилась единица. Ноль в логическом ИЛИ возвращается только тогда, когда на входе всё по нулям.
Это оказалось проще, чем И, — достаточно, чтобы в трубу попала хотя бы одна бусинка, которая вытолкнет итоговую:

Логическое НЕ
А вот этот элемент придумать было сложнее: нужно, чтобы он запускал бусинку, когда на вход не попадало ничего. Но как это сделать на практике, как отследить отсутствие бусинки с точки зрения физики?
Выход Эван придумал такой: он сильно заранее запускает итоговую бусинку, которая медленно скатывается вниз. За это время по соседней трубе пролетит или не пролетит бусинка, которая закроет выход для итоговой. Если пролетит (на входе будет единица), то на выходе будет ноль, потому что выход будет закрыт. А если по трубе ничего не пролетит, то выход не закроется, и итоговая бусинка в конце концов доедет до выхода:

Удвоитель
Иногда нужно распараллелить сигнал, чтобы он пошёл сразу в обе точки. В электронике это сделать просто: делаем два провода в нужном месте, и электроны разбегаются в обоих направлениях. Но в механической логике так не получится, нужно идти на хитрость. Например, сделать развилку с дополнительной бусинкой:
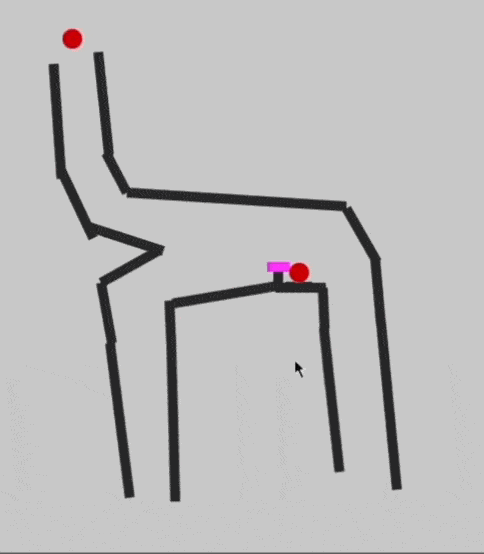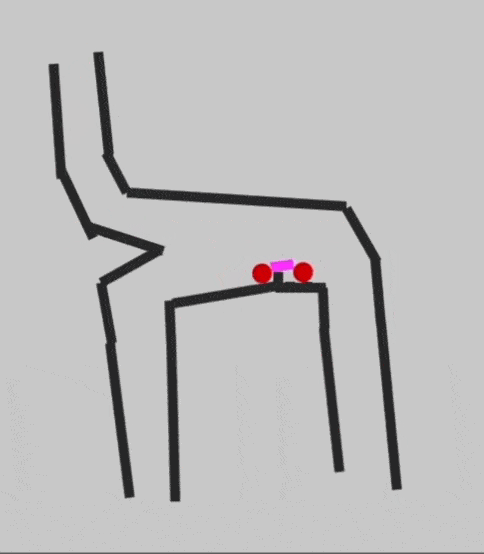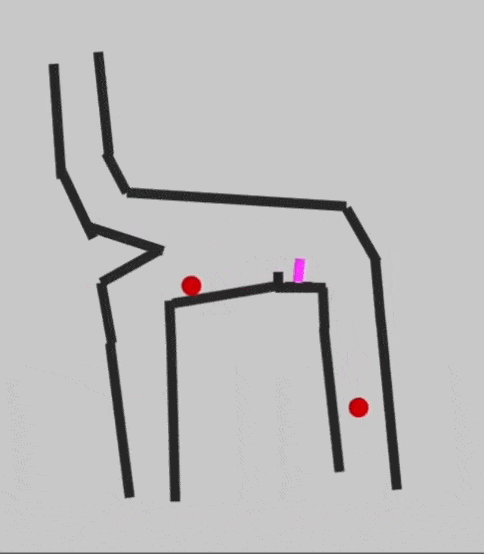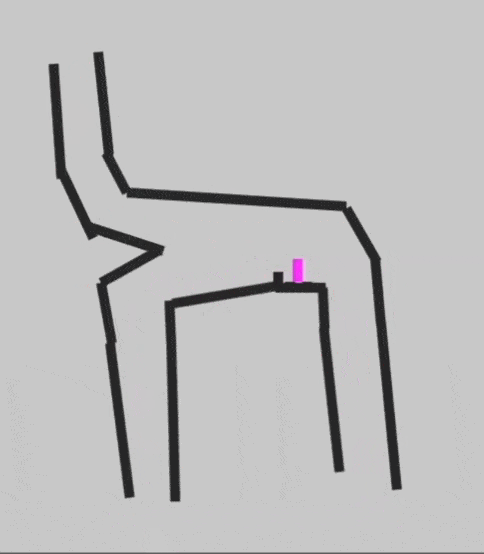
Перенос бусинки наверх
Так как у нас всё завязано на гравитации и бусинках, то может понадобиться такое: итоговая бусинка вышла из какой-то части механизма, и её нужно отправить наверх, для запуска новых вычислений. Для этого Эван придумал виртуальный перенос бусинки — та, которая внизу, запускает ту, которая наверху:
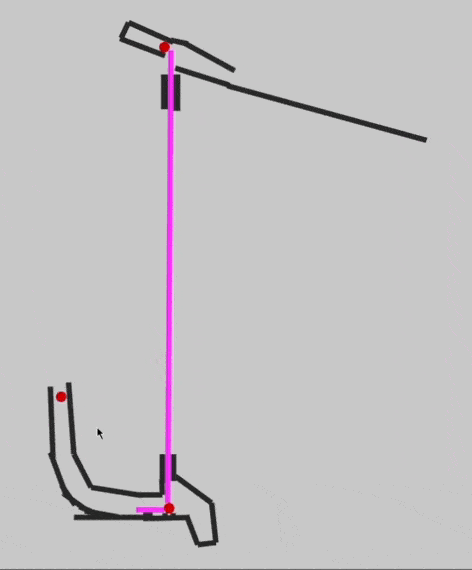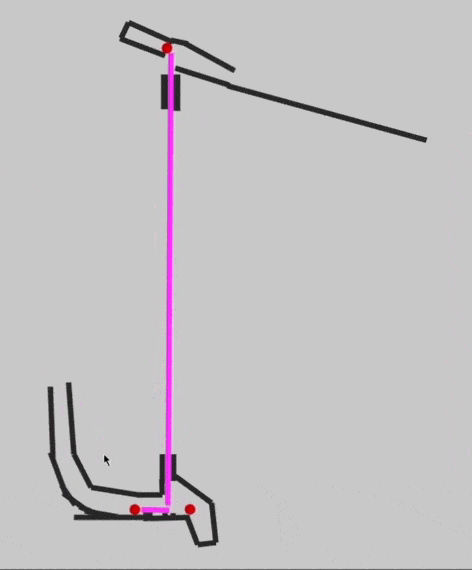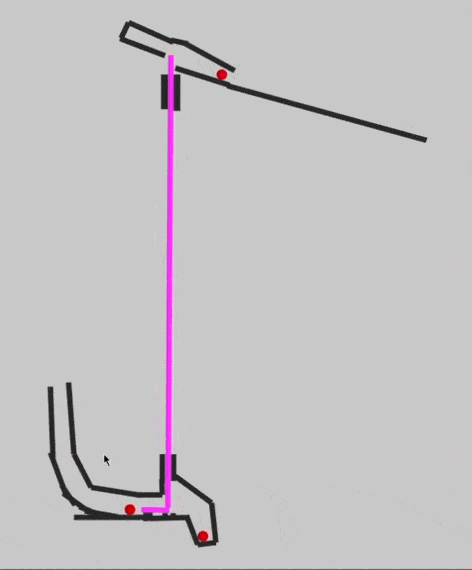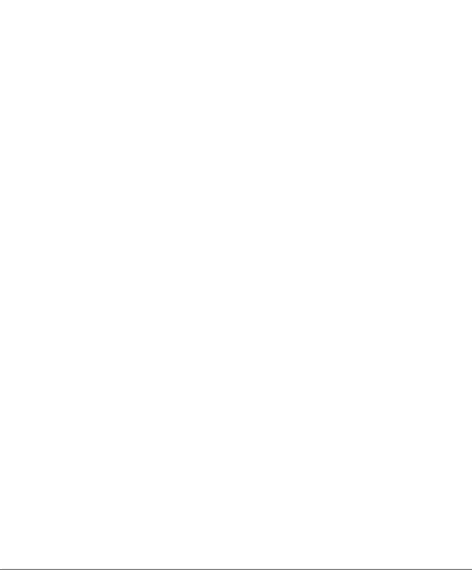
Собираем калькулятор для двух бусинок
Чтобы проверить в деле всю предыдущую теорию, Эван собирает простой сумматор: он складывает два сигнала. Забегая чуть вперёд, Эван сразу предусматривает перенос разряда (carry).
Вот какая схема нужна для сложения двух сигналов на бусинках:
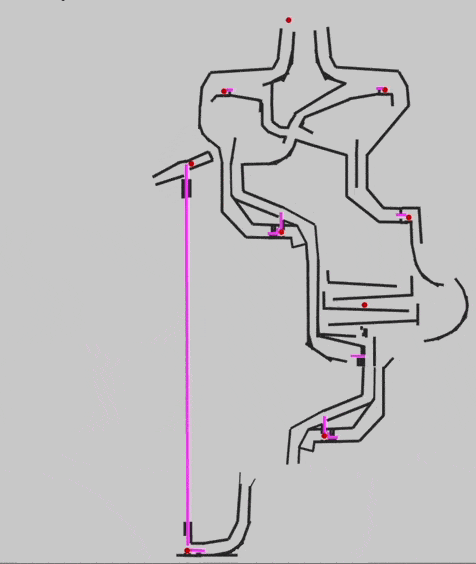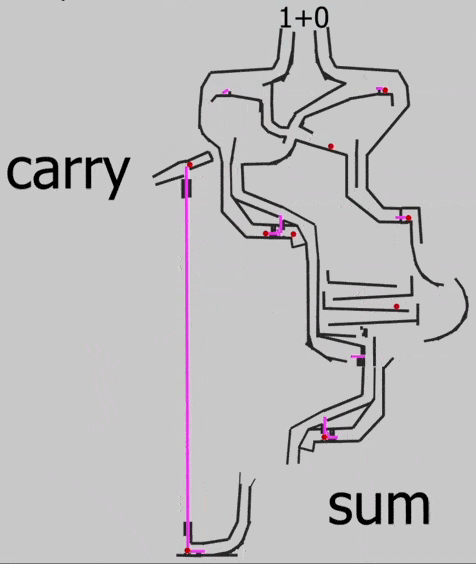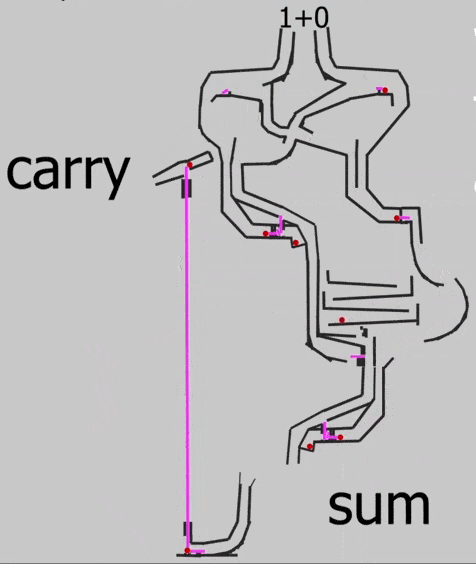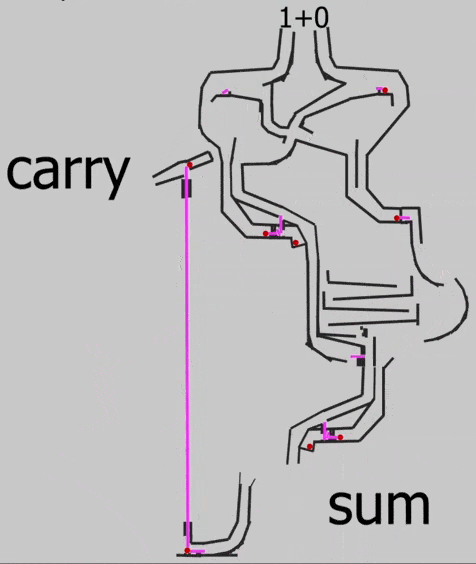
Отлично, у нас работает сложение двух сигналов, поэтому можно переходить к чему посложнее. Но сначала поговорим про перенос разряда.
Обрабатываем перенос разряда
Когда мы складываем обычные числа, например 19 и 7, то у нас иногда получается перенос единицы в новый разряд:

В двоичной системе счисления всё то же самое — разряды переносятся налево и складываются с теми числами, которые уже там стоят:
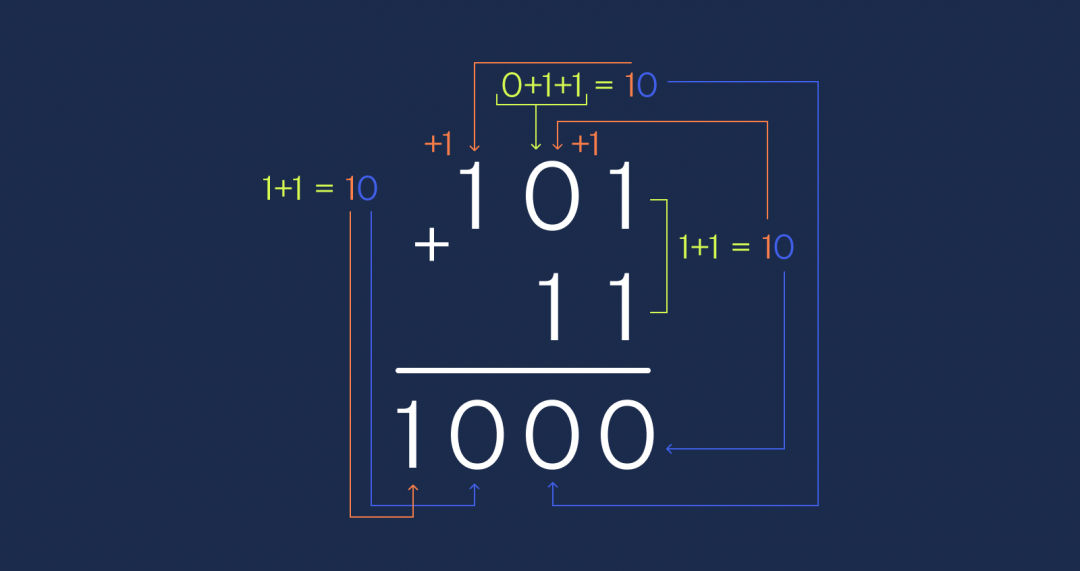
Чтобы сделать такой же перенос разряда и получить ноль после сложения двух единиц, добавим элемент XOR. Он возвращает ноль, если на входе было сразу две единицы или оба нуля, в противном случае он возвращает единицу. Именно так работает сложение с переносом в двоичной системе, а вот как это работает на бусинках:
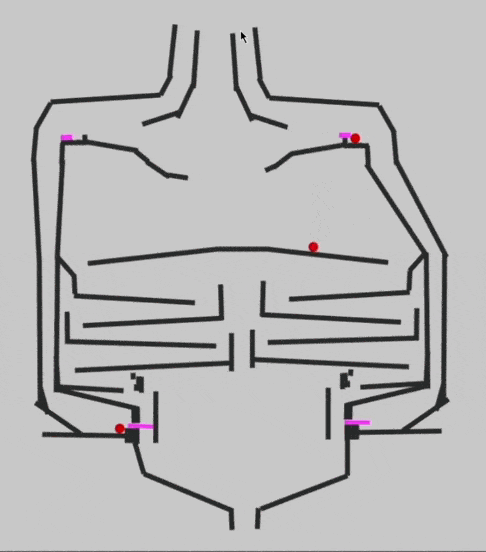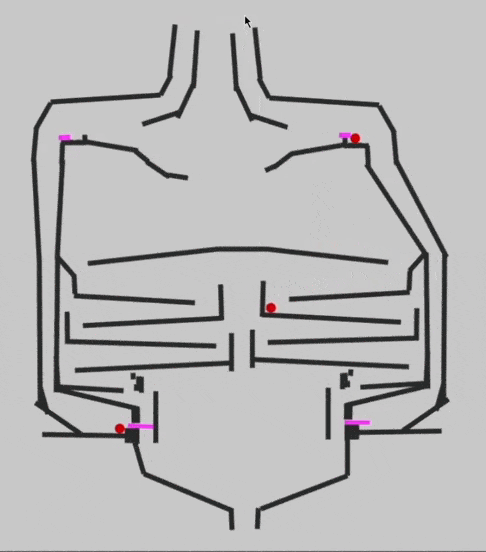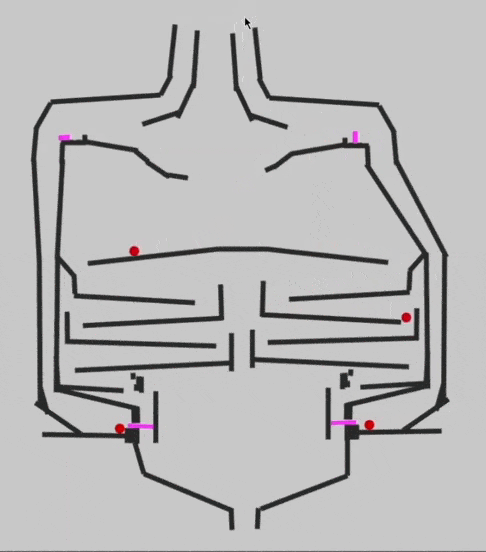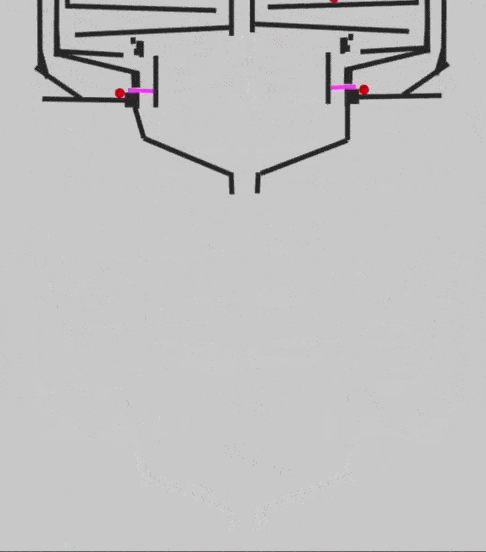
Чтобы проверить работу элемента в деле и убедиться, что 1+1+1 будет давать 1 в сумме и 1 в новом разряде, Эван собирает основную схему сумматора:
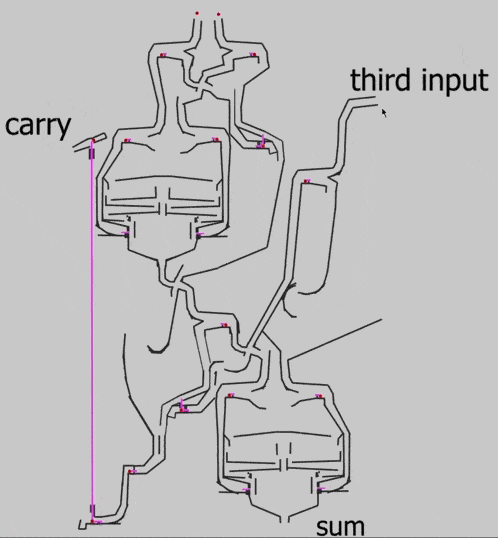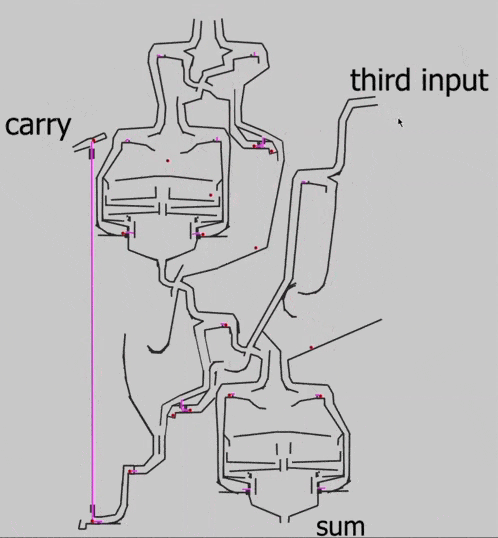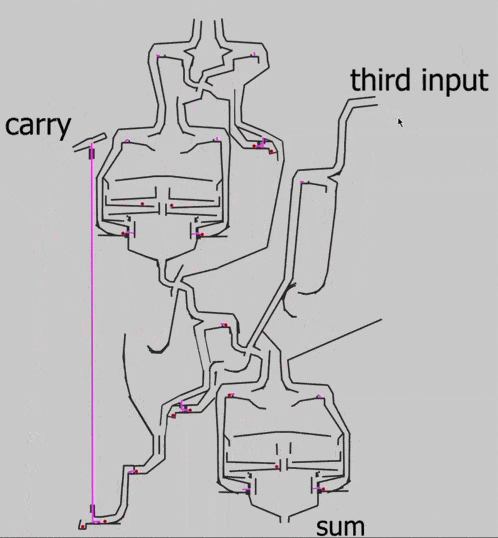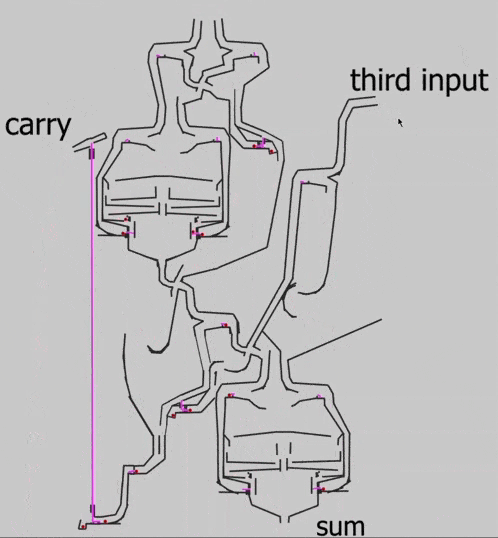
Видно, что на выходе получилось 11: одна бусинка вышла в первом разряде, а вторая — в переносе (carry).
Если собрать три таких сумматора подряд, можно складывать трёхразрядные числа, например, 7 (111) и 5 (101):
Чтобы посмотреть на результат работы, посмотрите видео с отметки 7:35. Мы специально не будем портить интригу, чтобы вы сами оценили весь масштаб движения бусинок :-)