В одном магазине сделали так: чтобы все точно соблюдали дистанцию в 1,5 метра, пол перед кассами разметили следующим образом — сделали даже немного с запасом:
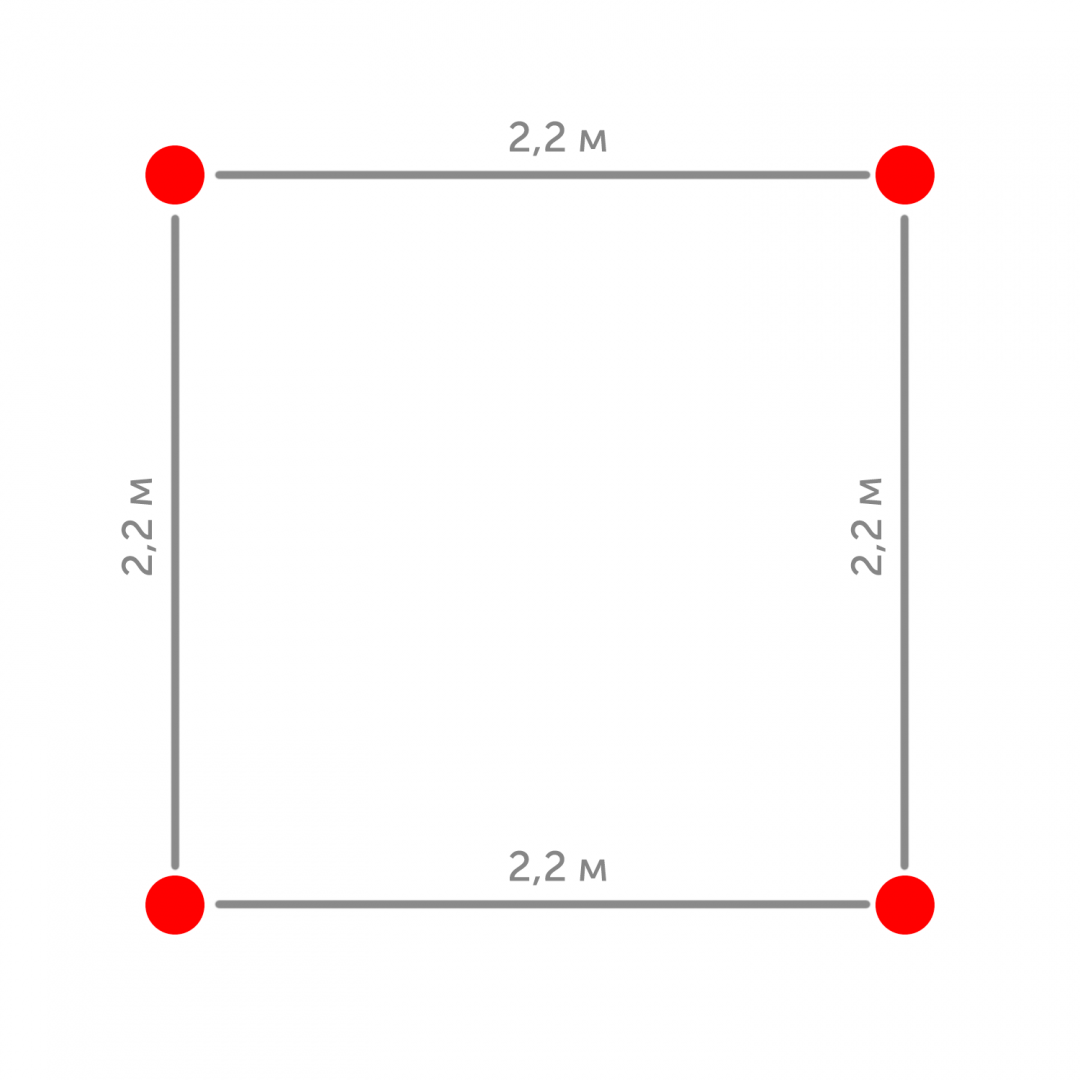
Когда все точки были заняты, в очередь пришёл покупатель и стал ровно в центре этого квадрата. Очередь стала ругаться, что он не соблюдает безопасную дистанцию 1,5 метра. Но покупатель молча стоял на своём месте. Вопрос: соблюдает ли он нужную дистанцию или очередь возмущается правильно?
Для начала нарисуем то, что получилось, когда новый покупатель стал в центре этого квадрата, и обозначим кружки буквами A, B, C, D и E:
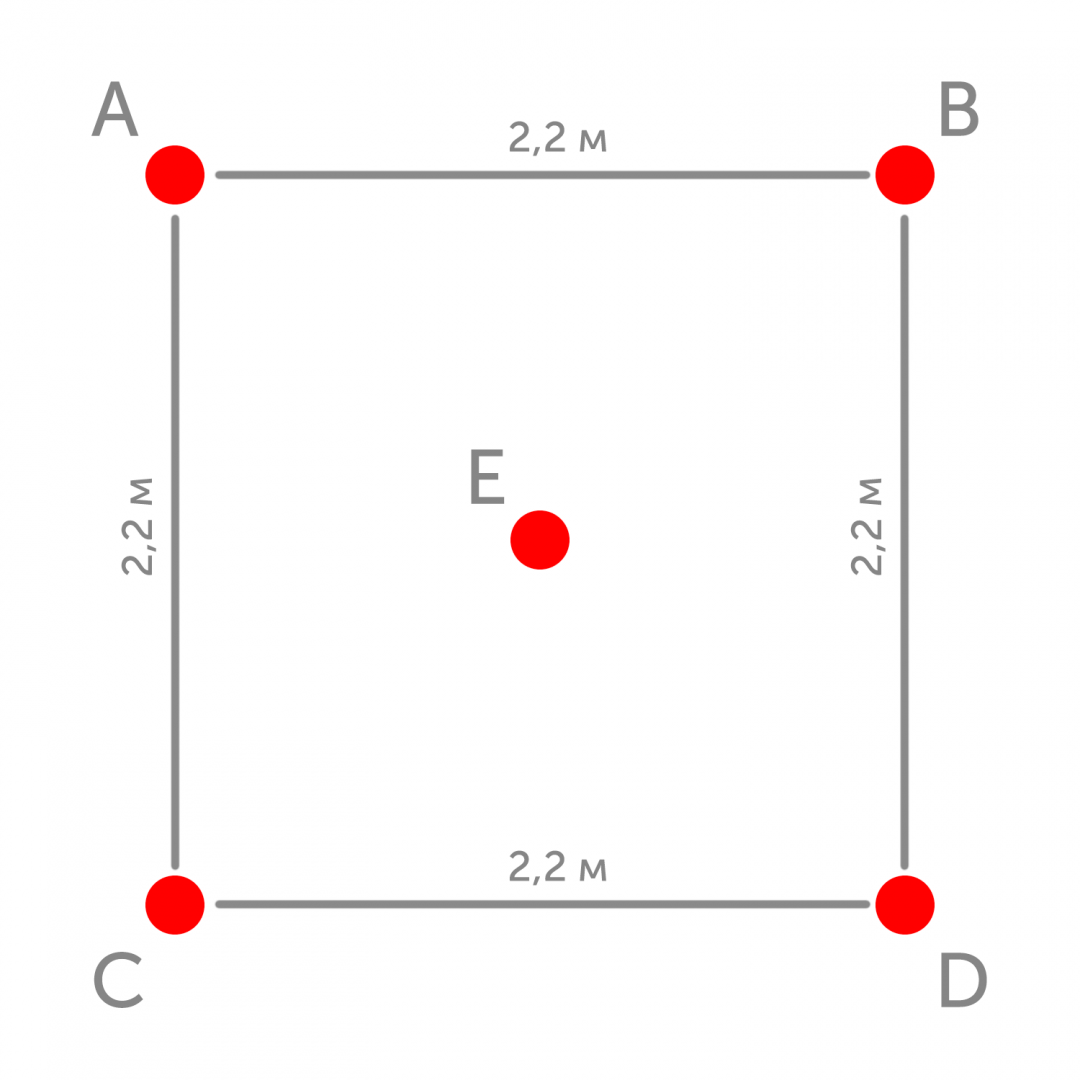
Теперь вспоминаем школьную геометрию. Так как по условию у нас квадрат, то AB = BD = CD = AC = 2,2 метра.
Раз новый посетитель стал ровно в центр квадрата (на место E), то получается, что AE = BE = CE = DE. С этим разобрались, переходим к треугольникам.
Возьмём треугольник ABC. Так как он образован двумя сторонами квадрата и его диагональю, то он — прямоугольный треугольник. Нас интересует гипотенуза BC, а чтобы её найти, нужно знать сумму квадратов катетов.
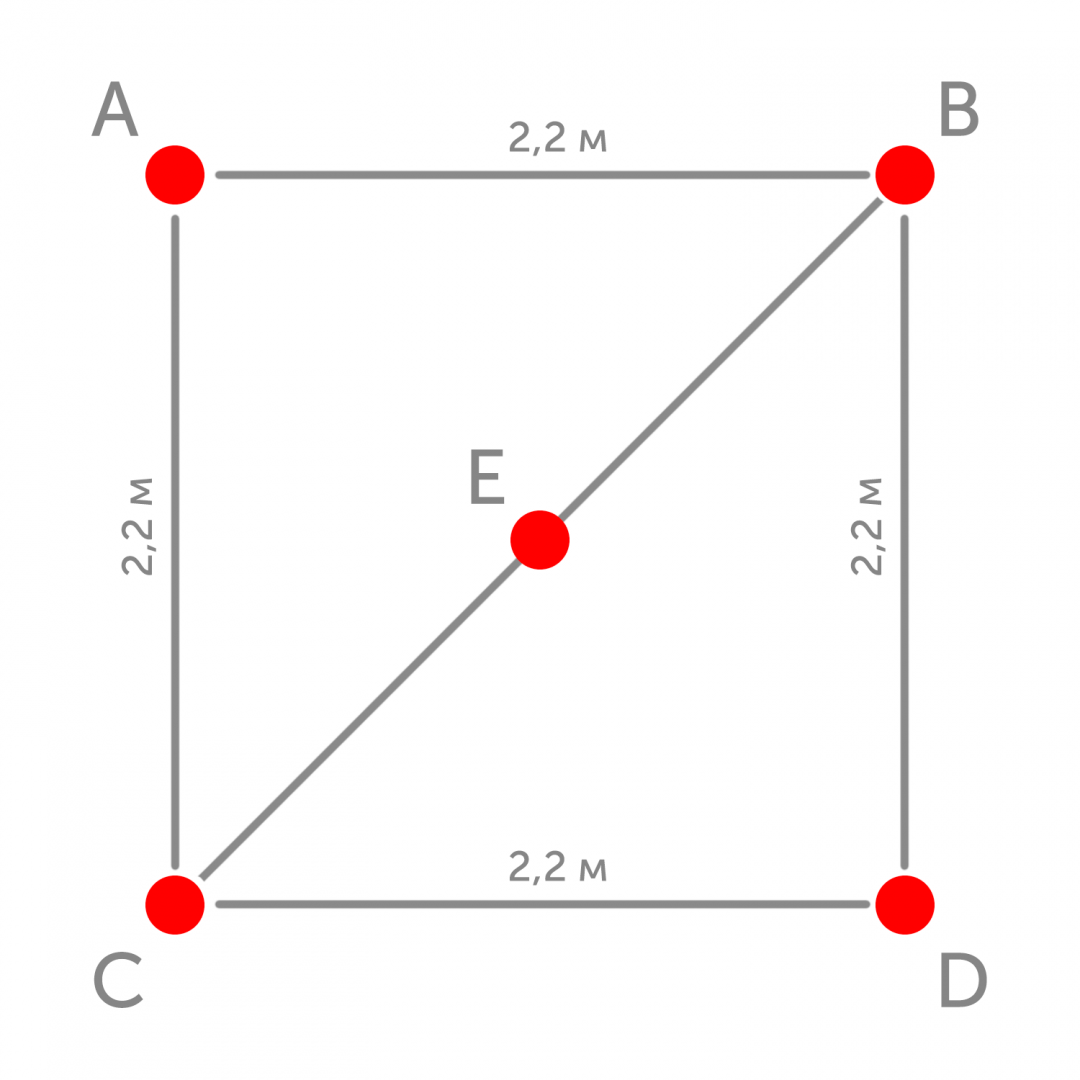
Из школьного курса мы помним, что квадрат длины гипотенузы равен сумме квадратов длин катетов: BC² = AB² + AC² → BC² = 2,2² + 2,2² = 9,68. Извлекаем квадратный корень из 9,68 и находим длину BC — 3,11 метра.
Вспоминаем, что E — это самый центр квадрата, а значит, точка E лежит на диагонали квадрата, а значит, делит диагонали квадрата пополам. Но у нас диагональ квадрата — это гипотенуза треугольника ABC, а значит, диагональ равна 3,11 метра. Теперь мы легко найдём расстояние от точек B и С до середины диагонали: 3,11 / 2 = 1,555 метра.
Проделав то же самое с другой диагональю, мы убедимся, что и там всё то же самое, а значит, расстояние от центра квадрата до его углов — 1,555 метра, что больше разрешённых полутора метров.
Получается, что все в очереди плохо учились в школе и зря шикают на нового посетителя. Хотя вставать в середину очереди всё равно нехорошо.