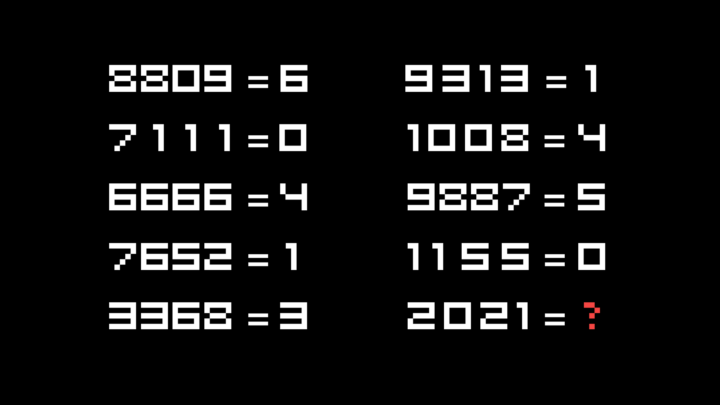Есть три игрока в бадминтон: Аня, Боря и Коля. Они решили сыграть несколько партий на выбывание: кто проиграл в паре — садится, ждёт, пока проиграет следующий, и занимает его место, а тот, кто выиграл в паре, играет следующую партию. Всё как обычно в дворовых соревнованиях.
Когда все устали, выяснилось, что Аня сыграла 8 партий, Боря — 12, а Коля сыграл 14 партий, при этом Боря умудрился сыграть 7 последних партий подряд.
А вот вопрос, на который нужно ответить: кто с кем играл четвёртую игру и кто в ней победил?
Сначала разберёмся с партиями и их количеством. На всякий случай поясним, что если Аня сыграла партию с Витей, то это значит, что каждый из них сыграл по одной партии:
Аня против Вити: 1 партия, при этом Аня сыграла одну партию и Витя тоже сыграл одну партию.
Это значит, что количество проведённых игр в два раза меньше, чем количество партий, которые получилось сыграть всем игрокам. В нашем случае было сыграно 8 + 12 + 14 = 34 индивидуальных партии, что даёт 34 / 2 = 17 партий всего.
Теперь посмотрим на Аню — она сыграла всего 8 партий из 17, при этом она точно начинала играть каждый раз, когда проигрывал кто-то из оставшихся ребят. Но единственный вариант, при котором это возможно, — если Аня начала играть со второй партии и проигрывала каждую игру. Например, начала со второй, проиграла её и пропустила третью, потом сыграла четвёртую, проиграла её и пропустила пятую и так далее:
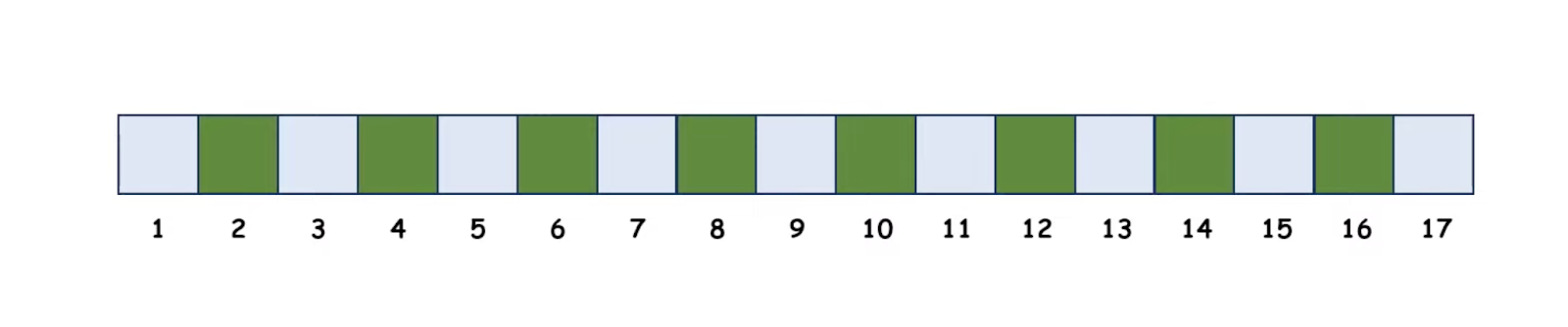
Получается, мы только что нашли половину ответа: в четвёртой игре точно играла Аня и ещё кто-то. Кто — сейчас выясним.
Раз Аня играла во всех чётных играх, то Боря и Коля играли во всех нечётных. Но у Бори сыграно 12 партий, а у Коли — 14. При этом мы знаем, что Боря сыграл 7 последних партий подряд.
Распишем эти игры:
11 игра: Боря и Коля
12 игра: Боря и Аня (она играла все чётные игры)
13 игра: Боря и Коля
14 игра: Боря и Аня
15 игра: Боря и Коля
16 игра: Боря и Аня
17 игра: Боря и Коля
Но до этого мы выяснили, что все нечётные игры были между Борей и Колей (потому что в нечётных играла Аня). Это значит, что Боря сыграл:
9 нечётных игр (1, 3, 5, 7, 9, 11, 13, 15, 17)
3 чётные игры (12, 14, 16)
Это в сумме даёт 12 партий — как раз столько и написано в условии задачи. А это значит, что в четвёртой партии он не мог принять участие и там играл Коля.
Выходит, что четвёртая партия была между Аней и Колей, и в ней победил Коля.
Поделитесь в комментариях, получилось ли решить у вас задачу самостоятельно и если да — то каким способом.