Понятие бесконечности существует в разных науках: физике, геометрии, биологии, астрономии и философии. Сегодня поговорим о математических бесконечностях — во множественном числе, потому что даже в математике их больше одной.
Это довольно сложная теоретическая статья. Если вам хочется чего-то практического, посмотрите наши проекты:
Обычно когда мы говорим про математику и бесконечность, то имеем в виду какое-то неисчислимое количество чисел — всех сразу. Но это понятие можно понимать по-разному, и содержимое бесконечности тоже может быть разным. Мы разберём главные вопросы: какие есть виды бесконечностей, что у них внутри, как их сравнивать и почему при делении на ноль получается бесконечность.
Чтобы было проще, сначала немного вникнем в теорию множеств, потому что основные понятия будут оттуда.
🤔 А зачем это программистам? А затем, что для разработки крутых и масштабных сервисов нужно знать математику, её возможности и ограничения. Чем шире ваш кругозор, тем проще находить решения разных проблем, которые другим кажутся очень сложными или нерешаемыми в принципе. А вы такие — р-раз! — и нашли решение. Круто же.
Теория множеств
Теория множеств — это раздел математики, который придумал немецкий математик Георг Кантор в XIX веке. Вот главные понятия, которые надо знать.
Множество — любое количество любых неповторяющихся элементов. Во множество нельзя попасть просто так: принадлежность к каждому задаётся определённым правилом. Например: «Все книги Российской государственной библиотеки» или «Все зрительские места Большого театра России».
Подмножества — это множества внутри другого множества. Например: «Книги Российской государственной библиотеки объёмом менее 500 страниц» или «Зрительские места Большого театра России в третьем ряду».
Количество элементов множества называется мощностью. Мощность множества из 10 книг будет равна 10. Если у двух множеств одинаковая мощность, они называются равномощными. Ещё говорят, что у таких множеств есть взаимно однозначное соответствие: на каждый элемент одного множества приходится один элемент другого:
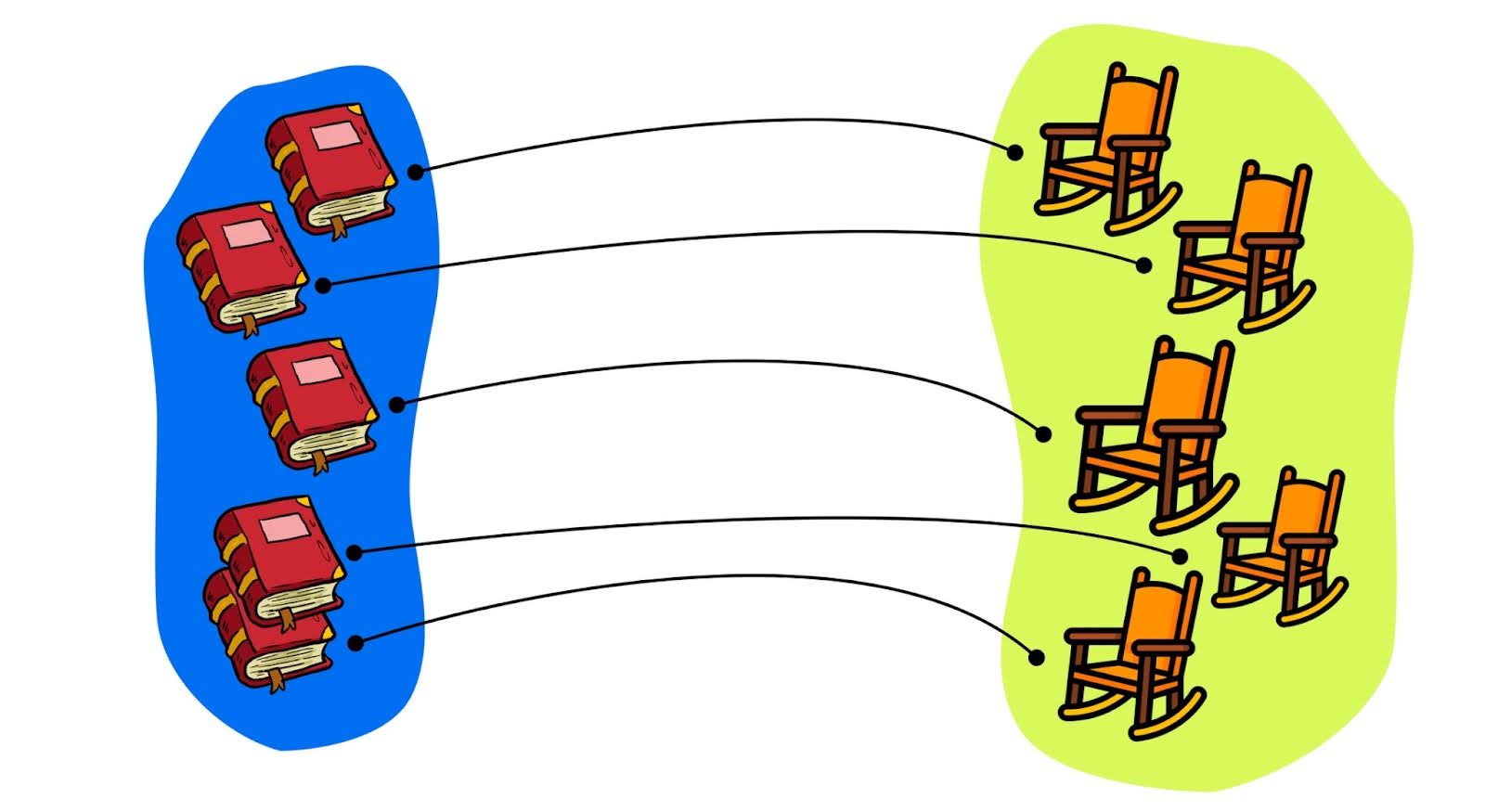
Если проводить параллель с программированием, можно вспомнить коллекции: массивы, кортежи и словари. Все они — разные способы упорядочивания множеств.
Потенциальная и актуальная бесконечности
Потенциальная бесконечность — тоже множество, в которое входит бесконечное количество элементов. Это абстрактное понятие.
Актуальная бесконечность — не просто количество элементов, а именно реально существующий бесконечный объект. Ближе всего к актуальной бесконечности подошла физика. Например, считается, что чёрные дыры имеют бесконечно большую силу притяжения. Большой взрыв тоже имеет отношение к актуальной бесконечности, потому что предполагает существование бесконечно малого объекта с бесконечно большой плотностью.
Бесконечные отели Гильберта
Потенциальную бесконечность и взаимно-однозначное соответствие хорошо иллюстрирует парадокс отелей Гильберта.
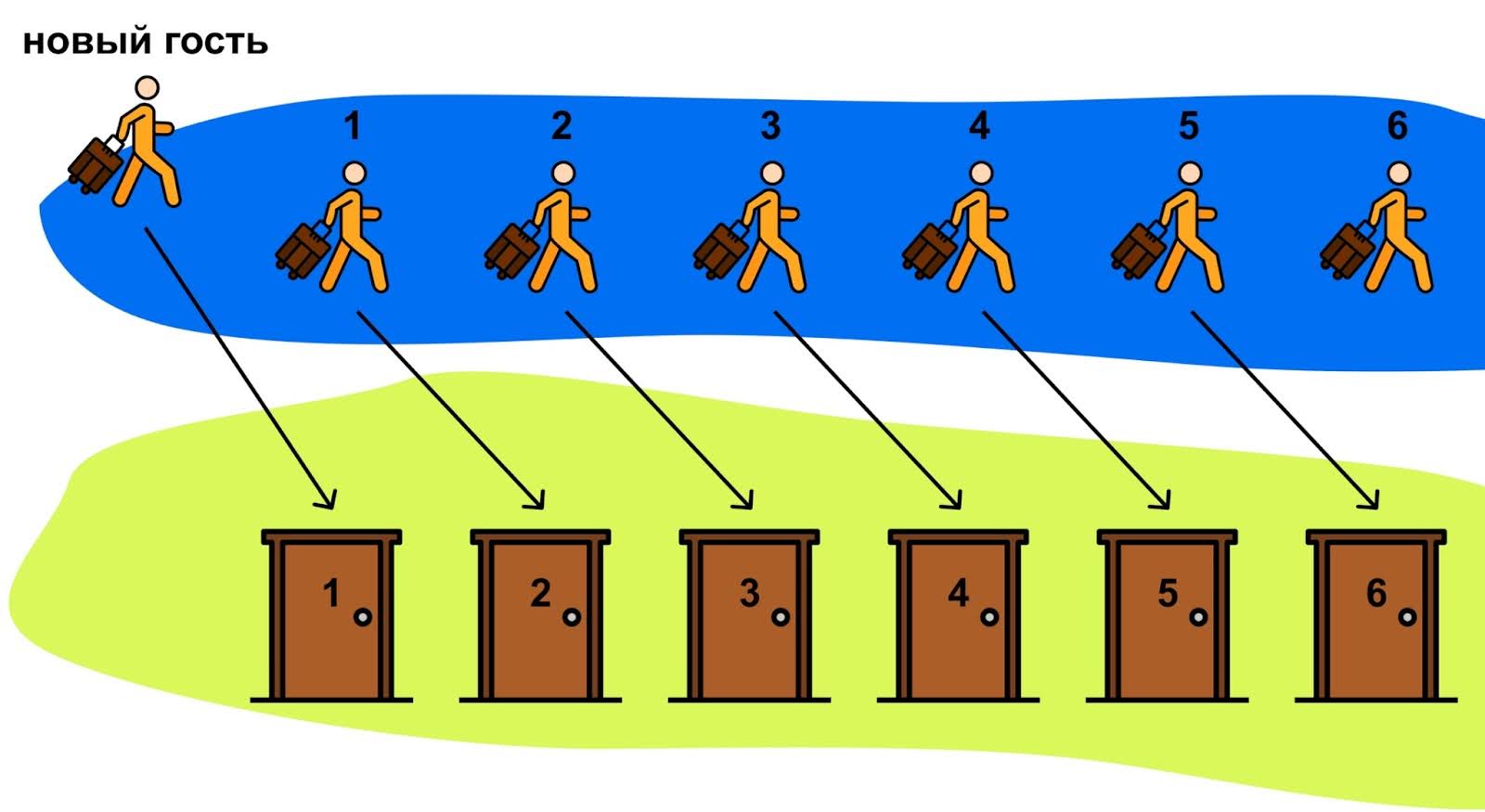
Представьте себе отель с бесконечным количеством комнат, в каждой из которых живёт гость. На бесконечное количество гостей у нас есть такое же бесконечное количество комнат в этом отеле. Получается два равномощных бесконечных множества. А теперь прибавим к одному из этих множеств единицу и попробуем снова их сравнить.
В парадоксе Гильберта в отель всегда можно подселить нового гостя по такому алгоритму:
- Новый гость занимает комнату №1.
- Предыдущий гость из комнаты №1 переселяется в комнату №2.
- Гость из комнаты №2 переселятся в комнату №3, и так до тех пор, пока гость из абстрактной последней комнаты №N не переселится в комнату №(N+1).
- Результат — комнат всегда хватает на любое добавочное количество гостей.
В итоге мы снова получили два равномощных множества:
По такому же принципу можно прибавить к бесконечности любое число, и результатом всегда будет бесконечность. Не новая, а именно та же самая. В этом и парадокс :-)
Положительная и отрицательная бесконечности
Бесконечности можно складывать и вычитать между собой, но есть нюанс. Если мы говорим о множестве в виде комнат и гостей в отеле Гильберта, то имеем в виду количество элементов, которое постоянно увеличивается. Это положительная бесконечность.
Если последовательность постоянно уменьшается и новые элементы всё дальше отдаляются от нуля в отрицательную сторону — это отрицательная бесконечность.
Так выглядят операции с бесконечностью и обычными числами:
n + ∞ = ∞ | n : ∞ = 0 |
n − ∞ = −∞ | n : (−∞) = 0 |
n × ∞ = ∞ | ∞ : n = ∞ |
n × (−∞) = −∞ | −∞ : n = −∞ |
В математических операциях бесконечности ведут себя практически так же, как другие положительные и отрицательные числа. Исключением будут только вычитание и деление, где результатом является неопределённость:
∞ + ∞ = ∞ |
∞ − ∞ = неопределённость |
∞ × ∞ = ∞ |
∞ − ∞ = неопределённость |
Счётная и несчётная бесконечности
Хотя в отеле Гильберта бесконечное количество гостей и комнат, мы всё-таки можем представить, как их посчитать. Эти последовательности всегда будут выглядеть одинаково:
1, 2, 3, 4, 5 … ∞
Мы точно знаем, что между 1 и 2 нет других элементов. Это значит, что все бесконечные множества, элементы которых можно пронумеровать, равномощны между собой. Поэтому множество из бесконечного числа гостей будет равномощно такому же множеству комнат, даже если к одному из них прибавить или отнять любое количество.
Неважно, какое число прибавили к бесконечности или отняли: важно, что каждому элементу бесконечного множества можно дать номер и сравнить с номером другого бесконечного множества, например комнат или гостей. Если так можно сделать — эти множества равномощные.
Множество, чьи элементы можно пронумеровать, называется счётным. Примеры такого множества — натуральные и рациональные числа.
Чтобы понять, когда элементы множества нельзя сосчитать, возьмём отрезок вещественных чисел от 0 до 1. Это десятичные дроби, каждая из которых будет иметь такой вид:
0,00000001231200 … при этом количество знаков после запятой будет продолжаться бесконечно
Возьмём часть последовательности от 0 до 1 и пронумеруем каждый элемент, причём для простоты будем использовать любые подходящие десятичные дроби:

Конечно, это не все элементы на отрезке, но для наглядного отображения хватит. Теперь возьмём по одной цифре от каждого элемента после запятой по диагонали:

У нас получилось число 0,0093363282. Каждую его цифру мы взяли из уже существующей последовательности: из первого числа взяли первую цифру, из второго — вторую, и так, пока не дойдем до последнего числа.
Представим, что нам нужно изменить каждый элемент полученного числа. Как именно, неважно. Например, мы можем сделать так: цифру 3 меняем на 0, а все остальные 0 меняем на 3. Главное, чтобы все цифры числа изменились. Для полученного таким образом нового числа будут справедливы эти утверждения:
- Полученное число принадлежит множеству десятичных чисел от 0 до 1.
- Этого числа нет среди чисел в уже существующей последовательности, потому что от каждого из них оно отличается минимум одной цифрой.
Дальше допустим, что мы выписали для таблицы не любые подходящие числа, а все, какие только смогли придумать, — вплоть до бесконечности. И всё равно, проделав такую же операцию, мы снова найдём число, которое ещё не выписали. Оно обязательно будет отличаться от любого уже выписанного хотя бы на ту одну цифру. Такой поиск нового числа называется диагональю Кантора.
Множество, чьи элементы нельзя пронумеровать, называется несчётным, или континуумом. Пример — вещественные числа (которые с дробью после запятой). Между двумя любыми элементами множества вещественных чисел всегда будет бесконечное количество элементов. Между элементами счётной бесконечности такое невозможно: после комнаты №1 всегда идёт комната №2. Элементы континуума невозможно представить как последовательность или таблицу.
Несчётная бесконечность больше счётной. Вещественные числа уже содержат все натуральные и рациональные. Если сравнить две бесконечности визуально, то счётную можно представить как пунктирную линию, а континуум — как сплошную.

Почему при делении на ноль получается бесконечность
Континуум вещественных чисел от 0 до 1 можно представить как отрезок:

Каждый элемент этого континуума можно представить как точку на отрезке. Если бы у точки был строгий размер, например 0,1, мы могли бы точно сказать, что на всём промежутке поместится 10 точек:
1 : 0,1 = 10
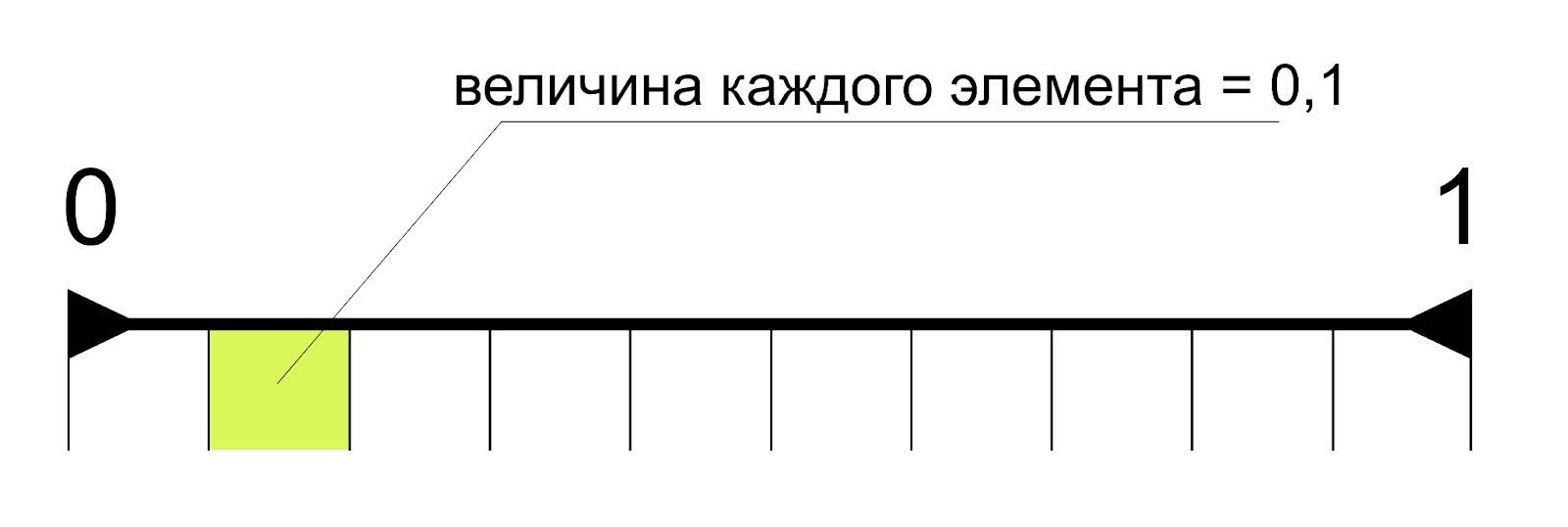
Но тогда у нас было бы счётное множество, а мы знаем, что в континууме бесконечное количество элементов. Чтобы такое было возможно, размер каждой точки должен равняться нулю:

Получается, что в единице — и любом другом числе, отличном от 0 — бесконечное количество нулей:
1 : 0 = ∞
На самом деле размер каждой точки — не 0, а бесконечно малая величина, но сегодня мы про это не будем, лучше в другой раз.
Бесконечности на практике
Мы нечасто встречаемся с бесконечностями на практике, но кое-какие примеры есть. Например, в программировании.
- Алгоритм Дейкстры, используемый в ПО навигаторов, работает с бесконечностью.
- С помощью бесконечности оптимизируют работу в машинном обучении. Для этого используют библиотеку NumPy.
- Бесконечный цикл
while (true)без оператора прерывания позволяет запускать программу бесконечное количество раз, пока её не остановят вручную. - Бесконечность позволяет инициализировать переменные, которые гарантированно больше или меньше другой переменной.
У каждого языка свой синтаксис и приёмы для работы с бесконечностью. В JavaScript даже есть таблица совместимости с браузерами:
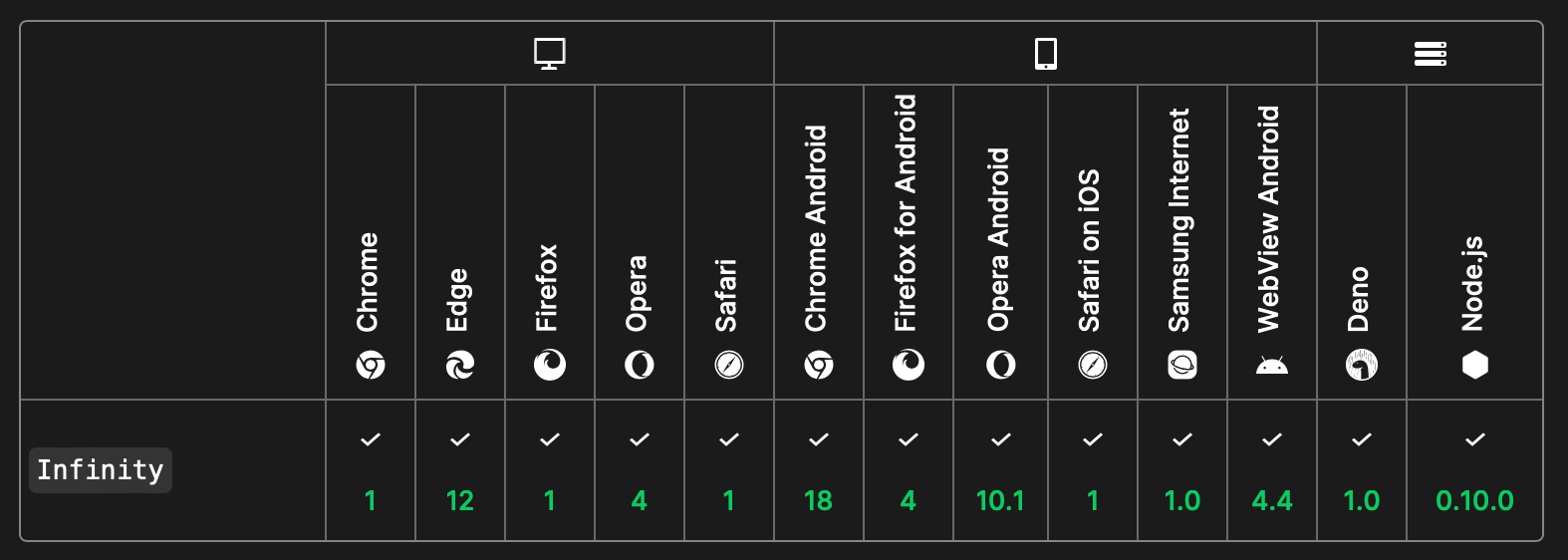
Есть ли другие бесконечности
В математике много разделов, где используется бесконечность, и везде подход немного различается. Но в каждом случае понадобится понимание основ: потенциальной и актуальной бесконечности, счётных бесконечных множеств и континуумов, отелей Гильберта и диагонали Кантора.