Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:
- Вектор — это просто группа из нескольких чисел, выстроенных в определённой последовательности. Например, рост и вес человека можно представить как вектор (172, 80). Ничего сложного.
- У вектора может быть внутри сколько угодно чисел. Главное — чтобы мы договорились, что для нас значат эти числа, и не меняли их местами просто так, произвольно.
- Векторы можно складывать, вычитать, умножать. Это чуть сложнее, чем с обычными числами.
- У вектора есть понятие линейной зависимости. Грубо говоря — параллельны друг другу векторы или нет. От этого зависит, какие операции можно делать с этими векторами.
Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.
Что такое матрица
Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.
Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.
Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.
В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.
В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.


Простые операции с матрицами
Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.
И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.


Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.

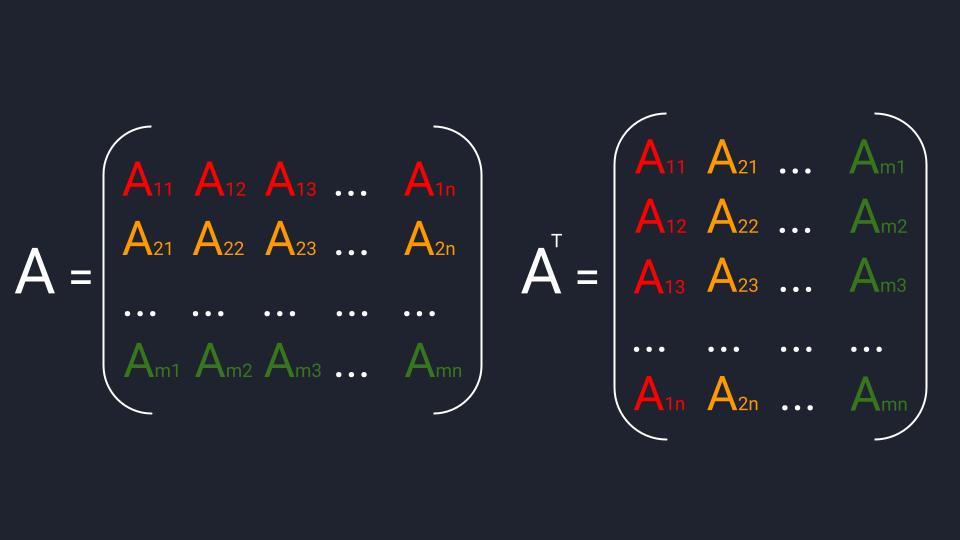
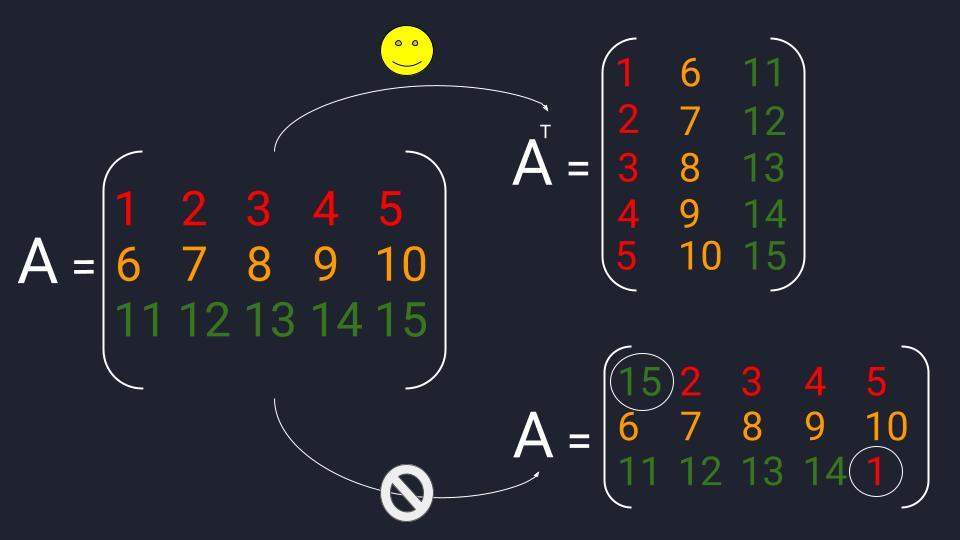
Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.
⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.

Сложение и вычитание матриц
Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.


Умножение матриц
Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:
- У нас есть две матрицы A и B. Их нужно перемножить, чтобы получить новую матрицу C.
- Размер матрицы A два на два: есть две строки и два столбца. Первая строка состоит из элементов А₁₁ и А₁₂; вторая — А₂₁ и А₂₂.
- У матрицы B такая же размерность: есть две строки и два столбца. Первая строка состоит из элементов B₁₁ и B₁₂; вторая — B₂₁ и B₂₂.
- У нас две одинаковые по размеру матрицы с двумя строками и столбцами. Это значит, что и матрица C будет размером два на два. Первая строка будет состоять из элементов C₁₁ и C₁₂; вторая — C₂₁ и C₂₂.
- Считаем элемент C₁₁. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть, после которой ставим знак плюс. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем обе части и получаем первый элемент первой строки матрицы С (C₁₁).
- Считаем элемент C₁₂. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент первой строки матрицы С (C₁₂).
- Считаем элемент C₂₁. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем части и получаем первый элемент второй строки матрицы С (C₂₁).
- Считаем элемент C₂₂. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент второй строки матрицы С (C₂₂).
Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.
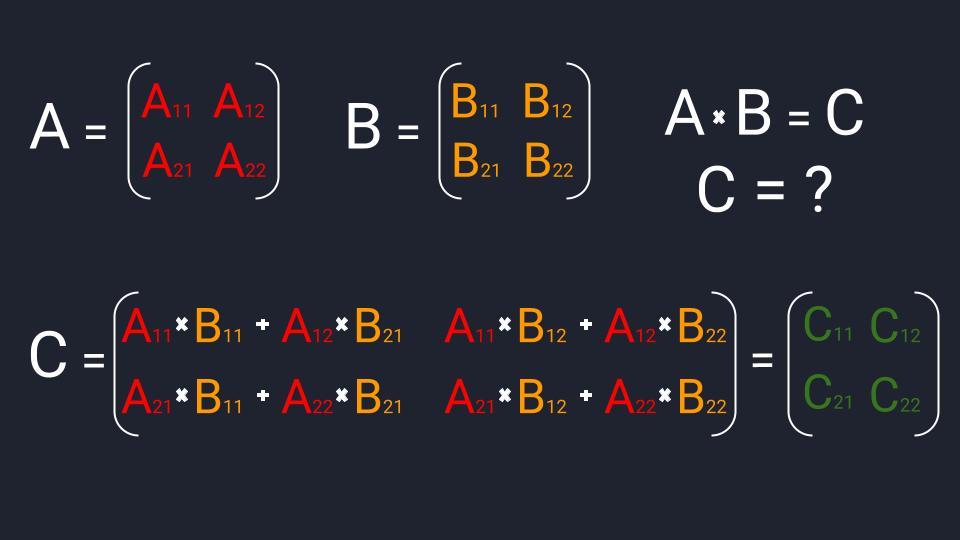

Что дальше
В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽