Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.
Напомним основные мысли:
- Вектор — это абстрактное понятие, которое представляет собой организованную последовательность каких-то чисел.
- В виде вектора можно представить координаты предмета в каком-то пространстве; площадь квартиры и её стоимость; цифровые данные анкеты какого-то человека и динамику цен на нефть.
- Если по-простому, то векторы нужны, чтобы обрабатывать большое количество организованных чисел. Представьте, что вектор — это коробка с конфетами, только вместо конфет — числа. Каждое число стоит в своей ячейке.
- Машинное обучение основано на перемножении матриц, которые, в свою очередь, можно представить как наборы векторов. Так что векторы лежат в глубине всех модных и молодёжных технологий ИИ.
С векторами можно совершать некоторые математические операции. Вот о них и поговорим.
Правильно — векторы
Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».
Сложение
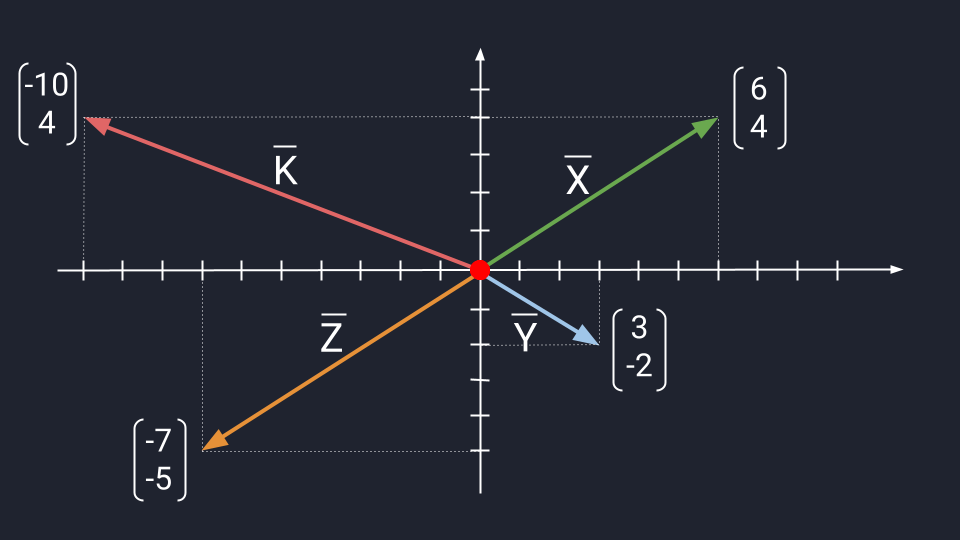
Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.
Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.
Предположим, нам нужно сложить векторы X и Y.
X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)
Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.
Например, вот сложение векторов с пятью координатами:
X = (6, 4, 11, 14, 99)
Y = (3, -2, 10, -10, 1)
X + Y = (9, 2, 21, 4, 100)
Интуитивное изображение сложения
Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.
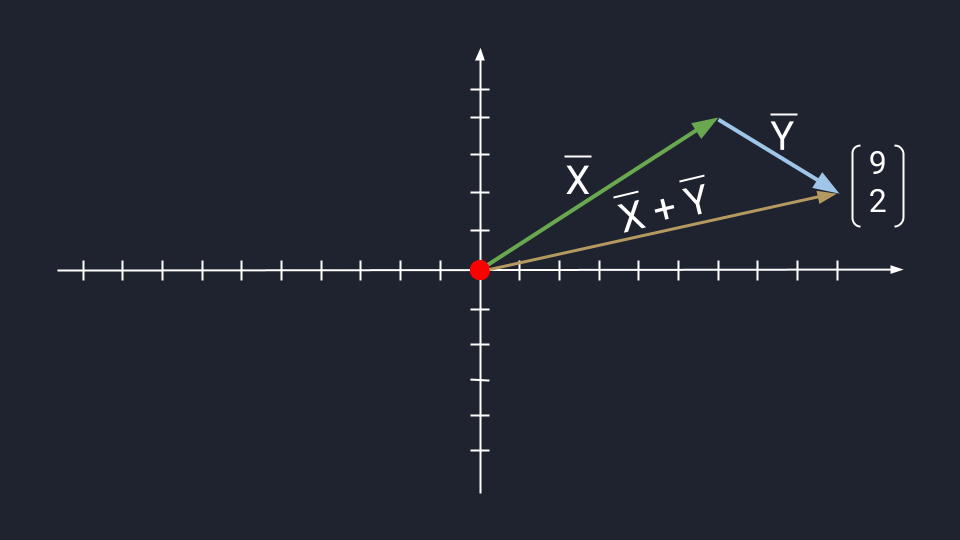
Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.
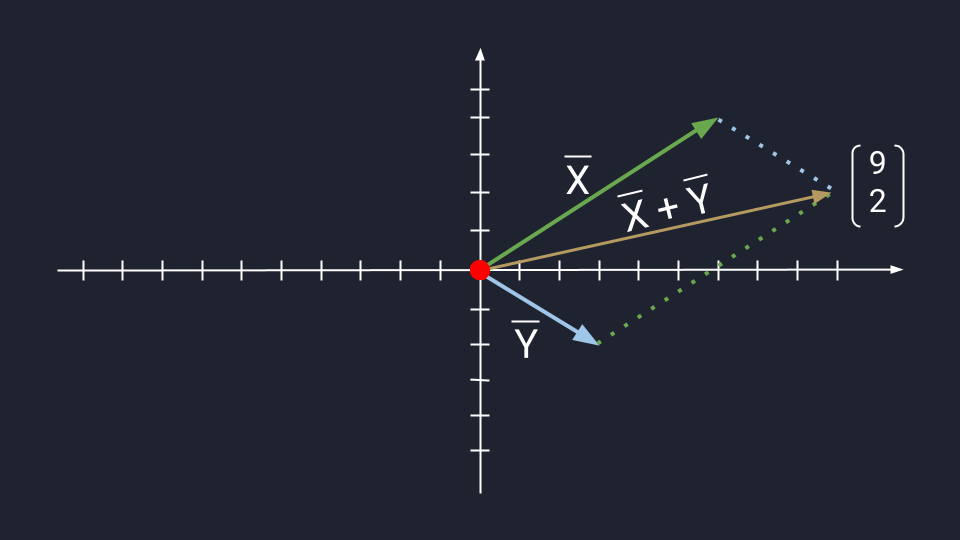
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.
Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.
Вычитание
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)
Дальше используются правила сложения. Пошагово это выглядит так:
- У нас есть X = (6, 4) и Y = (3, −2).
- Превращаем формулу Х − Y в формулу Х + (−Y).
- Разворачиваем вектор Y. Было: Y = (3, −2). Стало: −Y = (−3, 2).
- Считаем: X + (−Y) = (3, 6).
Теперь посмотрим, как выглядит вычитание векторов на графике:
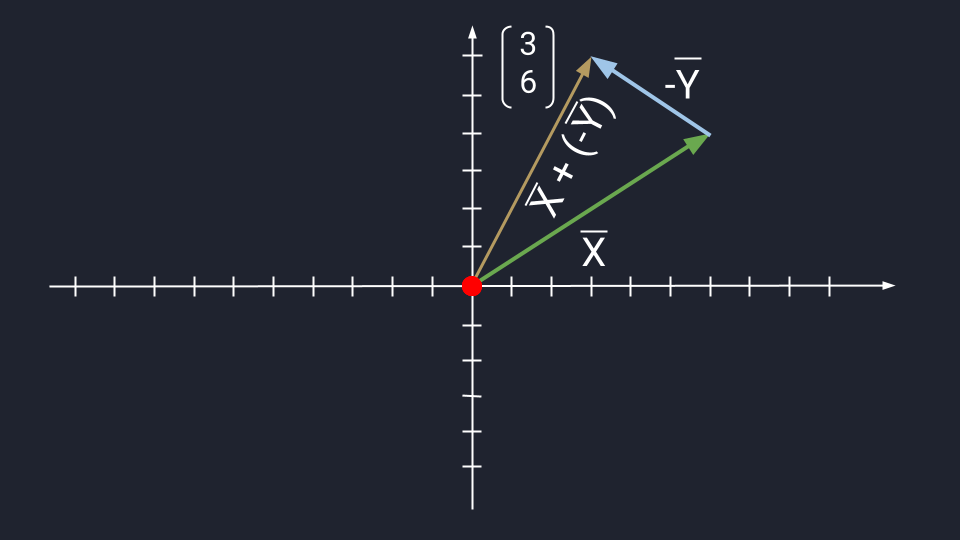
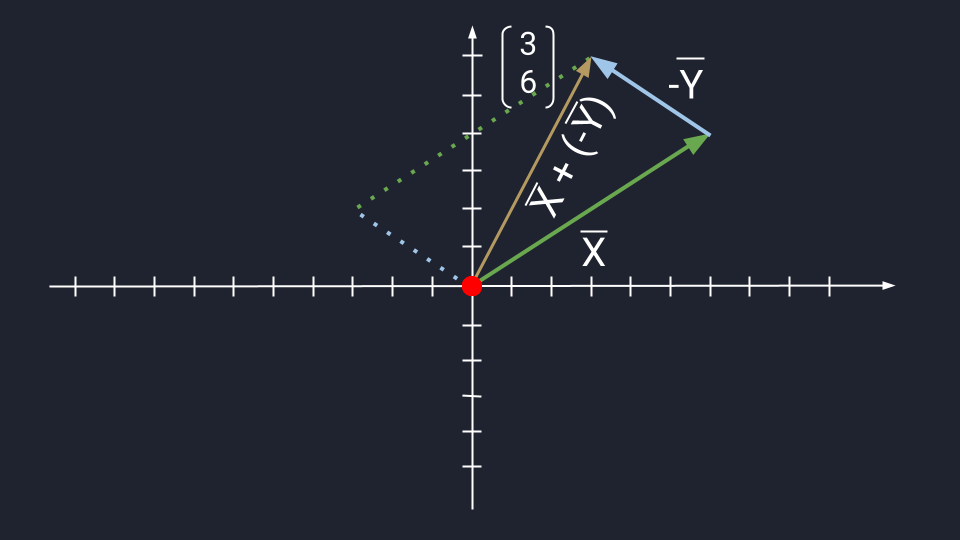
Длина вектора
Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.
Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:
X = 6 − 2 = 4
Y = 5 − 2 = 3
Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:
|C|2 = 42 + 32 = 25
|C| = √25 = 5
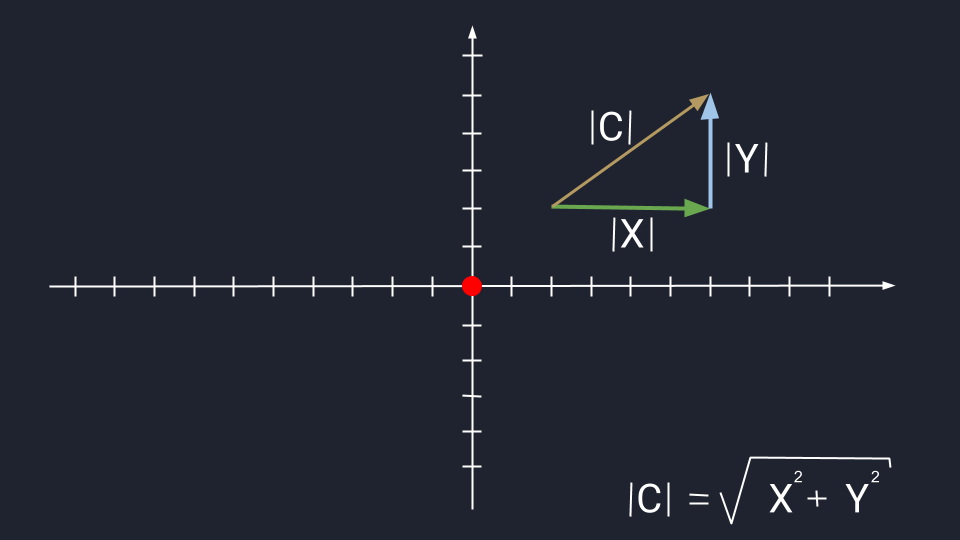
Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.
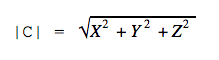
В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.
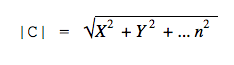
Умножение и деление вектора на число
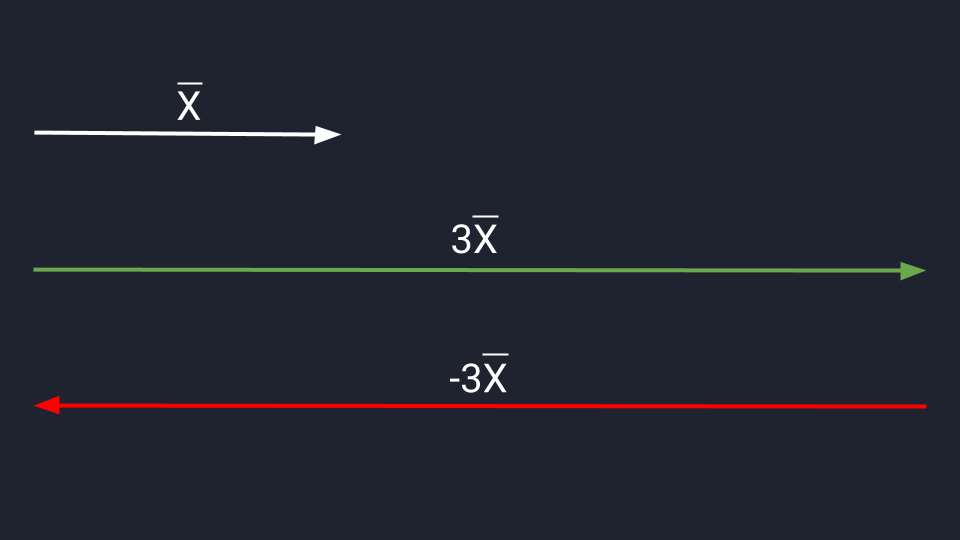
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.
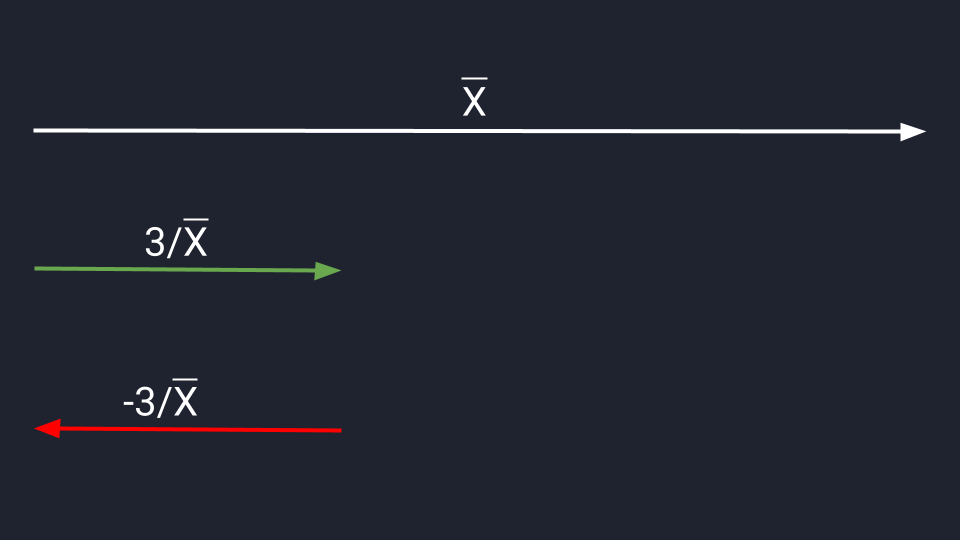
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.
Да вроде несложно!
Пока ничего сложного. Но если углубляться, вы узнаете, что:
- векторы можно умножать на векторы тремя способами в зависимости от задачи и от того, что мы понимаем под умножением;
- если от векторов перейти к матрицам, то перемножение матриц имеет несколько более сложную и довольно неинтуитивную математику;
- а перемножение матриц — это и есть машинное обучение.
Что дальше
В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.