Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».
Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.
Краткое содержание прошлых частей:
- Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
- Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
- Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
- Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
- Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
- Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.
И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.
❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.
Что такое матричное уравнение
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
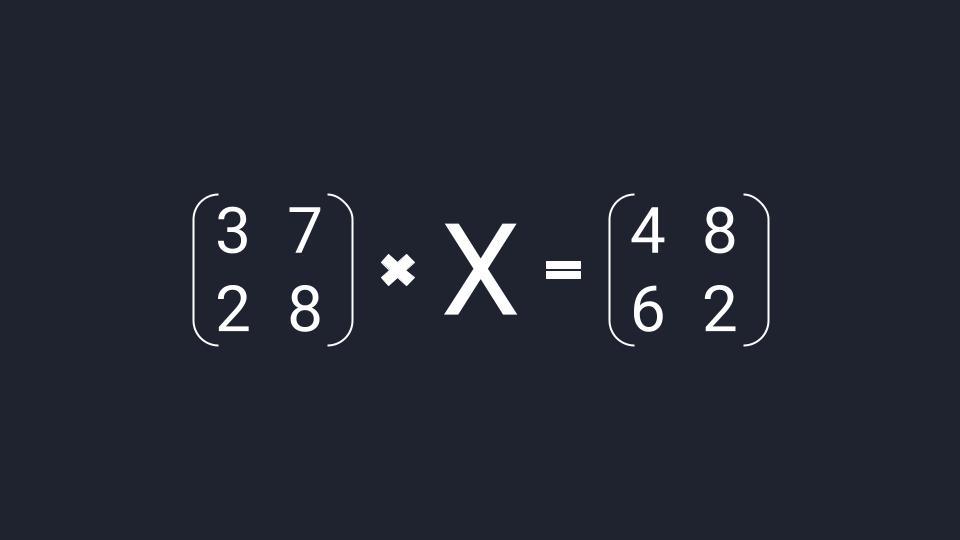
Как решать матричное уравнение
Как решать матричное уравнение
Чтобы решить матричное уравнение, нам понадобится пройти 5 несложных шагов. Несложных — если их делать поэтапно, а не пытаться решить уравнение сразу за один подход. Вот пошаговый план решения матричного уравнения:
- Упрощаем уравнение.
- Вводим единичную матрицу.
- Находим обратную матрицу.
- Вычисляем неизвестную матрицу.
- Проверяем уравнение.
Понимаем, что звучит сложно, поэтому теперь — про каждый шаг в подробностях.
Шаг 1. Упрощаем уравнение
Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.
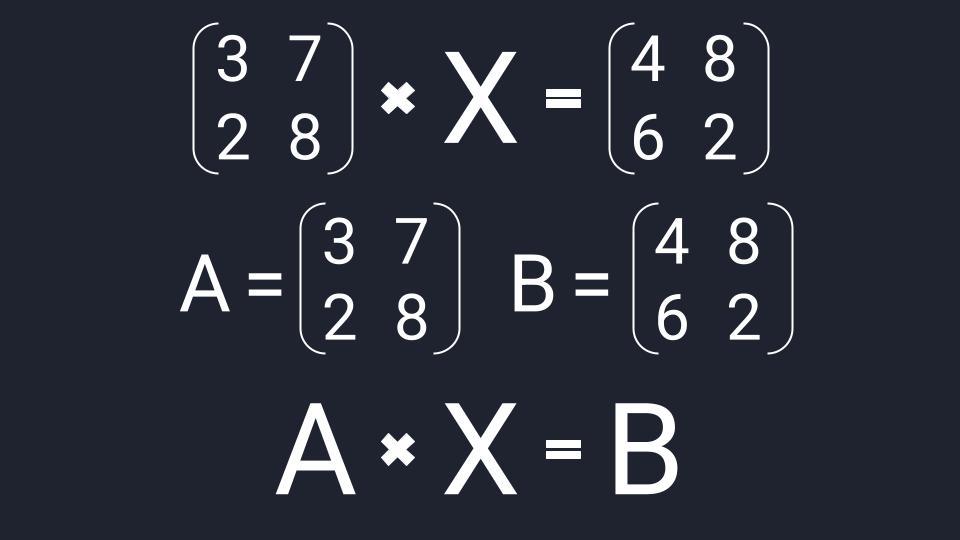
Шаг 2. Вводим единичную матрицу
В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.
Можно представить, что есть число 100 — это «сто в первой степени», 1001
И есть число 0,01 — это «сто в минус первой степени», 100-1
При перемножении этих двух чисел получится единица:
1001 × 100-1 = 100 × 0,01 = 1.
Вот такое, только в мире матриц.
Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А-1. Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:
А-1 × А × Х = А-1 × В
Добавляем единичную матрицу и упрощаем запись:
А-1 × А = E — единичная матрица
E × Х = А-1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем
Х = А-1 × В — новая запись уравнения
После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.
💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A-1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.
Шаг 3. Находим обратную матрицу
Вспоминаем формулу и порядок расчёта обратной матрицы:
- Делим единицу на определитель матрицы A.
- Считаем транспонированную матрицу алгебраических дополнений.
- Перемножаем значения и получаем нужную матрицу.
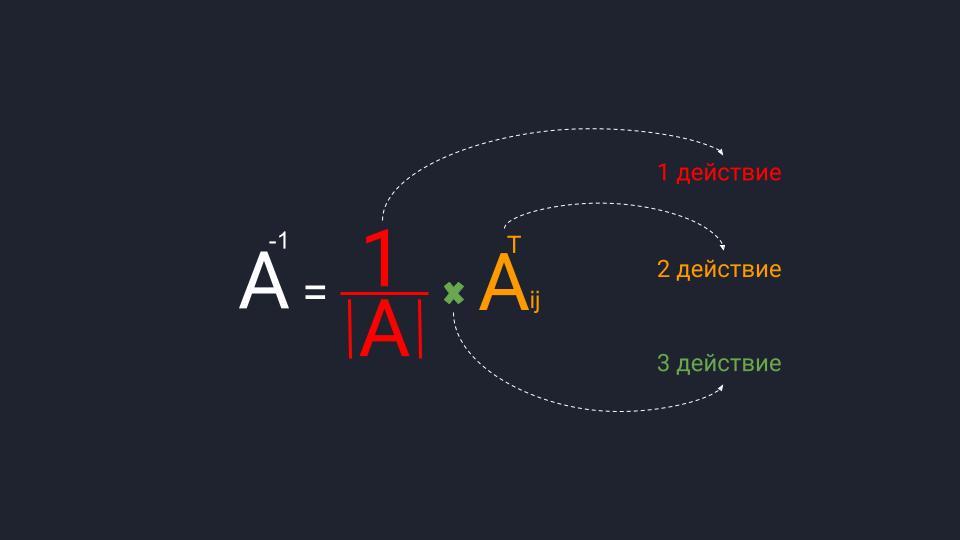

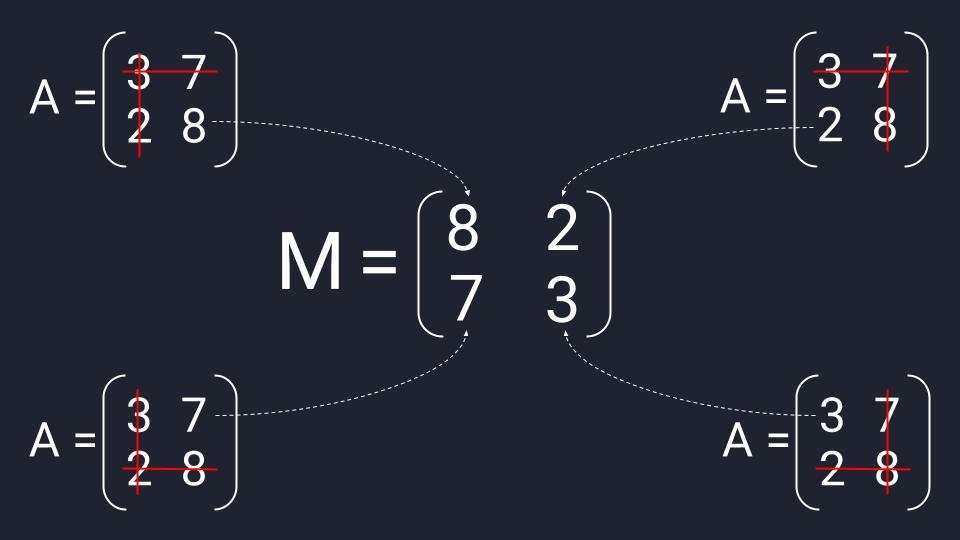

Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Шаг 4. Вычисляем неизвестную матрицу
Нам остаётся посчитать матрицу X: умножаем обратную матрицу А-1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Шаг 5. Проверяем уравнение
Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.
👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

Этого котика не существует, а матрицы — существуют.













