Недавно мы начали говорить о линейной алгебре и матрицах. Сначала всё было хорошо и легко:
Но начав заниматься линейной алгеброй, бывает трудно остановиться. Сегодня мы познакомимся с обратной матрицей и научимся её вычислять. Это навык, который в будущем нам пригодится для решения матричных уравнений.
С точки зрения арифметики материал не сложный. Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры.
Читать ли эту статью?
❌ Если вам нужны простые быстрые решения для жизни — нет, можно объявить, что у вас сегодня выходной.
✅ Если вашему мозгу не хватает вызова и новых горизонтов — велком ту зе матрикс.
Обратное — это как?
В математике есть взаимно обратные числа. Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число:

Обратные числа при умножении друг на друга всегда дают единицу:
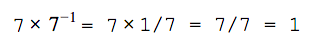
Что такое обратная матрица
В линейной алгебре есть обратные матрицы. По свойствам они напоминают обратные числа: если обычную матрицу умножить на обратную к ней, получится единичная матрица.

Единичная матрица работает как единица с числами: если умножить любое число на единицу, получится исходное число; если умножить любую матрицу на единичную матрицу — получится исходная матрица:
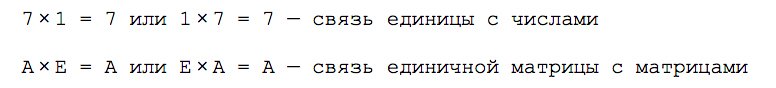
Единичная матрица состоит из единиц и нулей: на диагонали находятся единицы; остальные элементы — нули. Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.

Как рассчитать обратную матрицу
Для расчёта обратной матрицы нужно выполнить три действия. Пока что не обращайте внимание на термины:
- Разделить единицу на матричный определитель.
- Найти транспонированную матрицу алгебраических дополнений.
- Перемножить полученные значения.
Далее мы по порядку во всём разберёмся.
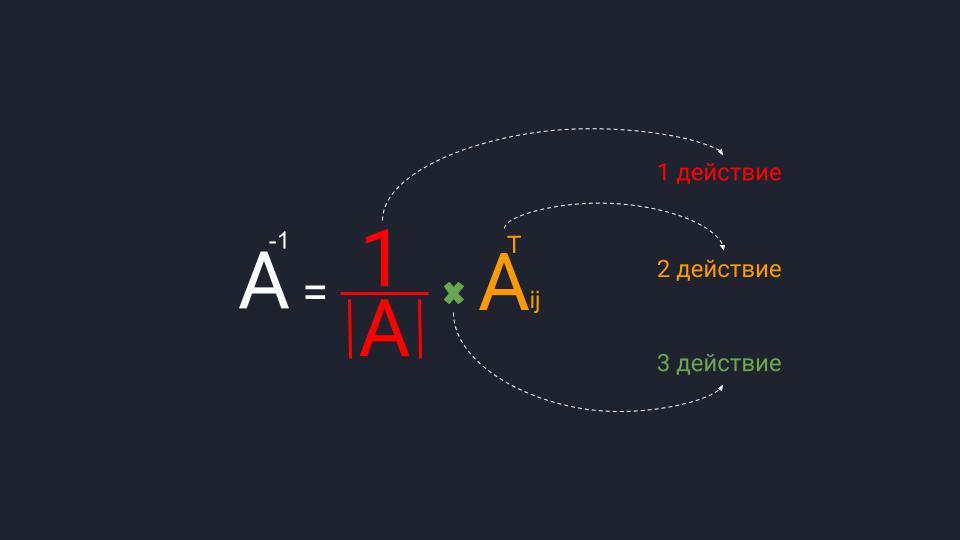
Первое действие: делим единицу на матричный определитель
Определитель — это особое число, которое «определяет» свойства матрицы.
Порядок вычисления определителя зависит от размера матрицы, которому он соответствует — чем больше матрица, тем сложнее считать определитель. Мы только знакомимся с матрицами, поэтому остановимся на определителях второго и третьего порядка — они подходят для квадратных матриц размером 2×2 и 3×3.
Чтобы найти определитель второго порядка, нам достаточно умножить элементы главной диагонали и вычесть из значения произведение чисел второй диагонали.
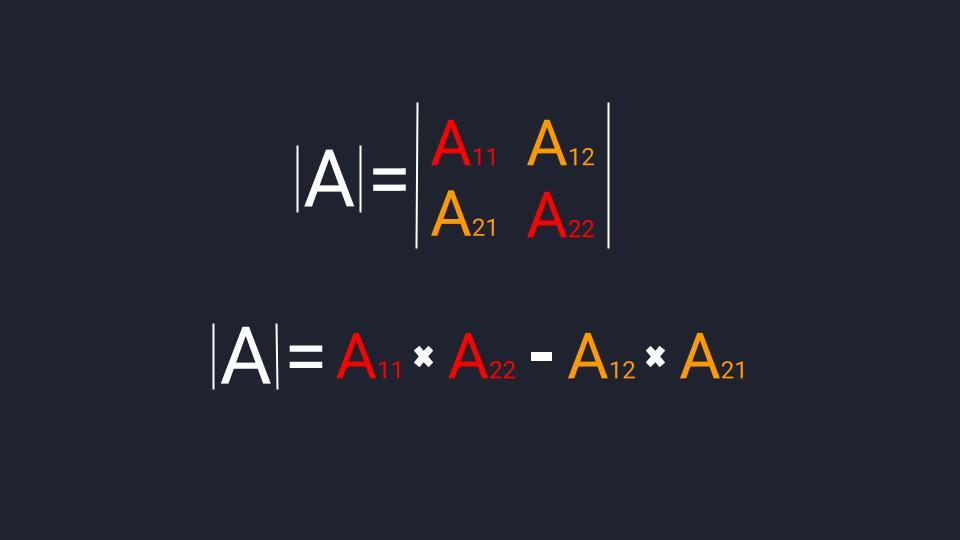

Определитель третьего порядка находится путём умножения диагоналей на треугольники. Здесь много операций, поэтому формулу соберём по частям.
Сначала работаем по главной диагонали: идём от верхнего левого элемента и движемся к правому нижнему элементу. Перемножаем элементы между собой.

Прибавляем к произведению элементов первой диагонали произведение первого треугольника. Основание первого треугольника находится параллельно главной диагонали и состоит из элементов А₂₁ и А₃₂. Вершина — элементА₁₃.

Прибавляем к полученному результату произведение второго треугольника, в котором основание состоит из элементов А₁₂ и А₂₃, а вершина — А₃₁.

Вычитаем из полученного значения произведение элементов второй диагонали. Вторая диагональ начинается в левом нижнем углу и идёт в правый верхний угол.

Вычитаем произведение элементов третьего треугольника, в котором основание — элементы А₁₂ и А₂₁, а вершина — А₃₃.

Последний шаг: вычитаем произведение четвёртого треугольника, с основанием из элементов А₂₃ и А₃₂ и вершиной А₁₁.



Второе действие: находим транспонированную матрицу алгебраических дополнений
Транспонированная матрица алгебраических дополнений вычисляется в три шага:
- Мы из исходной матрицы находим матрицу миноров.
- Меняем в матрице миноров знак некоторых элементов и получаем матрицу алгебраических дополнений.
- Находим транспонированную матрицу из матрицы алгебраических дополнений.
Алгоритм вычислений матрицы миноров и матрицы алгебраических дополнений зависит от размера исходной матрицы — чем она больше, тем сложнее формула расчёта. Поэтому мы рассматриваем только матрицы второго и третьего порядка.
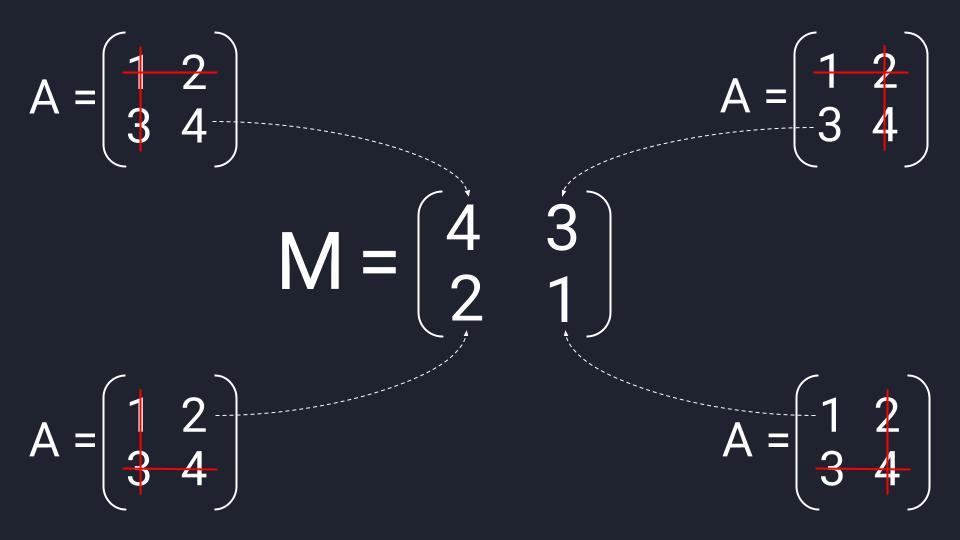
Чтобы найти матрицу миноров второго порядка, нам нужно последовательно зачеркнуть три элемента исходной матрицы:
- Вычёркиваем первую строку и первый столбец исходной матрицы — получаем первый элемент первой строки матрицы миноров.
- Вычёркиваем первую строку и второй столбец — получаем второй элемент первой строки матрицы миноров.
- Вычёркиваем вторую строку и первый столбец — получаем первый элемент второй строки матрицы миноров.
- Вычёркиваем вторую строку и второй столбец — получаем второй элемент второй строки матрицы миноров.
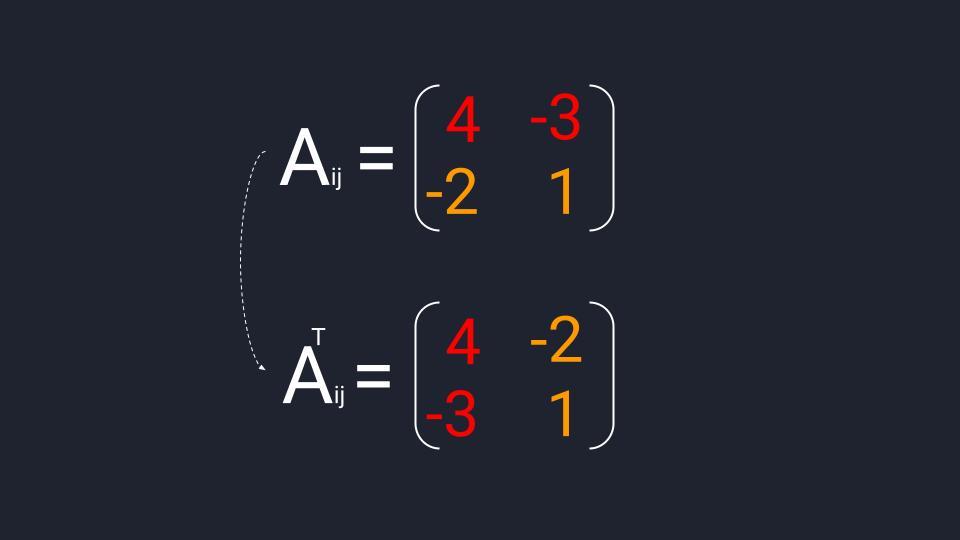
Когда матрица миноров составлена — меняем знаки элементов второй диагонали и получаем матрицу алгебраических дополнений. Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.

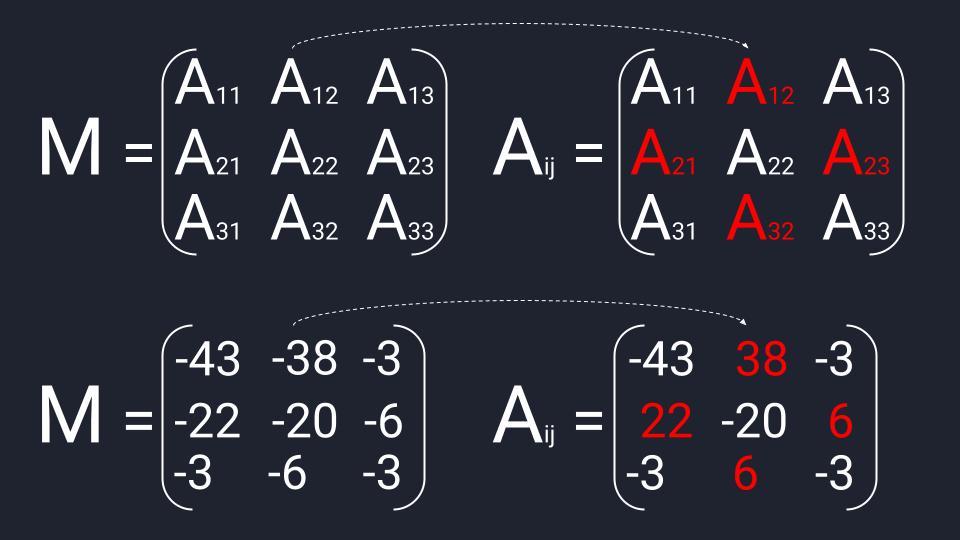
Матрица миноров третьего порядка рассчитывается по следующему принципу:
- Последовательно вычёркиваем строки и столбцы.
- Получаем четыре элемента и считаем определитель.
- Записываем результат в матрицу миноров третьего порядка.
Чтобы не запоминать порядок вычёркивания элементов — попробуйте схему:
- Определите элемент, который вы ищете для матрицы. Пусть это будет A₁₁.
- Найдите этот же элемент в исходной матрице и отметьте его точкой.
- Проведите от этой точки две линии: вдоль строки и вдоль столбца.
После вычёркивания останется квадратная двухразмерная матрица, определитель которой равен разности произведений двух диагоналей.

Матрицу миноров третьего порядка удобно находить на бумаге с помощью ручки, карандаша и ластика — записываете исходную матрицу, карандашом вычёркиваете линии, считаете определитель, вытираете линии и повторяете процедуру. Рекомендуем попробовать и сверить результат с нашими расчётами.
1-я строка 1-й элемент:
Δ = 5×1 - 8×6 = -43
1-я строка 2-й элемент:
Δ = 4×1 - 7×6 = -38
1-я строка 3-й элемент:
Δ = 4×8 - 7×5 = -3
2-я строка 1-й элемент:
Δ = 2×1 - 8×3 = -22
2-я строка 2-й элемент:
Δ = 1×1 - 7×3 = -20
2-я строка 3-й элемент:
Δ = 1×8 - 7×2 = -6
3-я строка 1-й элемент:
Δ = 2×6 - 5×3 = -3
3-я строка 2-й элемент:
Δ = 1×6 - 4×3 = -6
3-я строка 3-й элемент:
Δ = 1×5 - 4×2 = -3
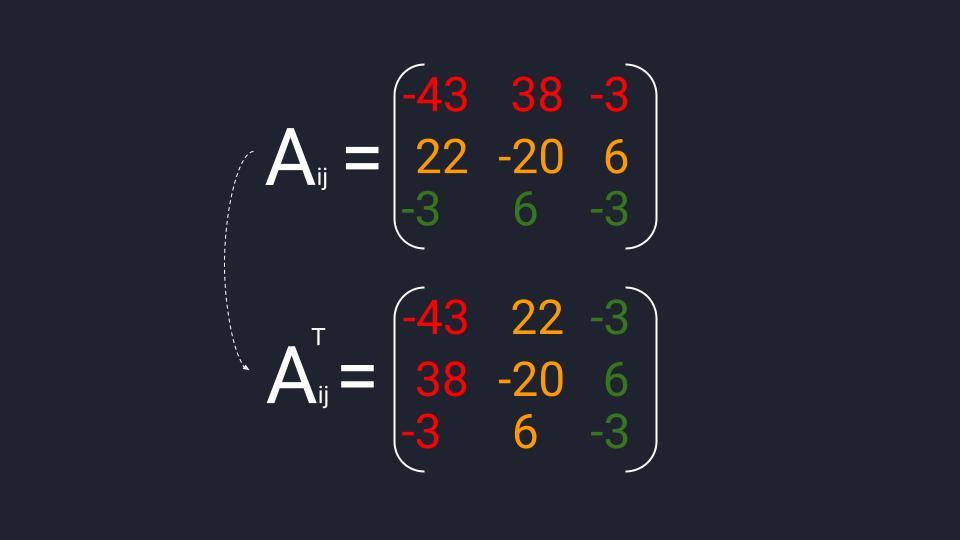
Считаем матрицу алгебраических дополнений: берём матрицу миноров и меняем на противоположный знак в четырёх элементах — изменяем А₁₂, А₂₁, А₂₃ и А₃₂. Транспонируем полученную матрицу и можем переходить к последнему действию.

Третье действие: считаем обратную матрицу
Мы нашли все компоненты для вычисления обратной матрицы. Осталось их подставить в формулу, перемножить и записать ответ:

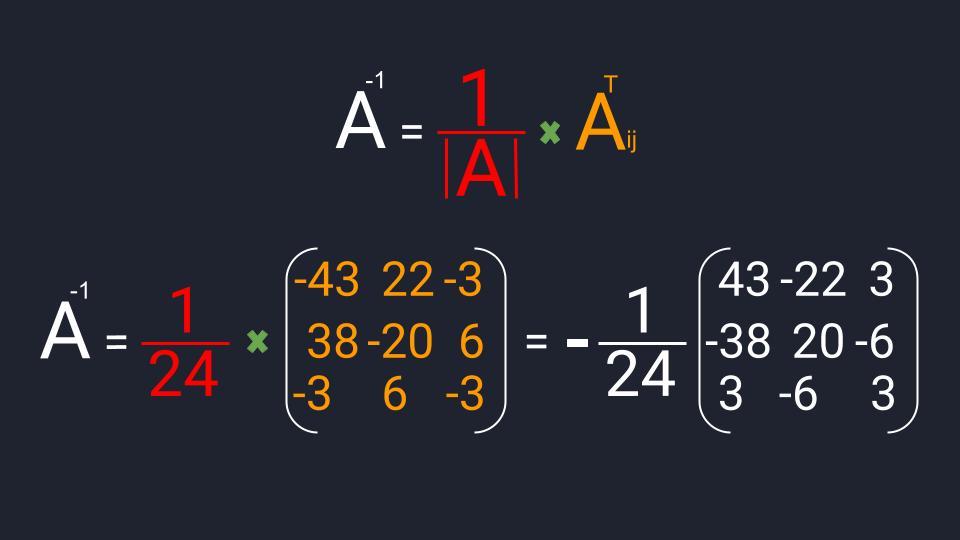
Господи, зачем всё это?
Мы понимаем, что это всё кажется совершенно оторванным от жизни. Какие-то миноры, детерминанты, о чём вообще речь?
Смотрите:
- Вам не нужно уметь решать все эти уравнения самостоятельно. Для этого давно есть мощные алгоритмы.
- Достаточно понимать, из чего всё это складывается. Вот матрица. Вот некий алгоритм, который делает из этой матрицы какую-то другую матрицу. Это всё просто арифметика, числа туда, числа сюда.
- В конце этого пути мы покажем, как из этих кубиков собрано машинное обучение. И вы увидите, что машинное обучение — это просто много алгебры. Просто арифметика, числа туда, числа сюда.
- И вы понимаете, что никакого искусственного интеллекта не существует. Это всё, от начала и до конца, работа с числами и расчёты по формулам. Просто когда это делается в больших масштабах, создаётся иллюзия осмысленной деятельности. Ключевое слово — иллюзия.
Спокойствие, всё будет хорошо.















