Есть прямая линия, на которой подряд располагаются 5 равнобедренных треугольников, основанием на этой линии. Длины оснований — 12, 13, 14, 15 и 16 сантиметров.
После этого от каждой пары треугольников построили наверх ромбы, потом от этого ряда — ещё ромбы и так до тех пор, пока не дошли до последнего. Но самое интересное, что последний ромб, который на вершине — это квадрат.
Вот его площадь и нужно найти! Справитесь?
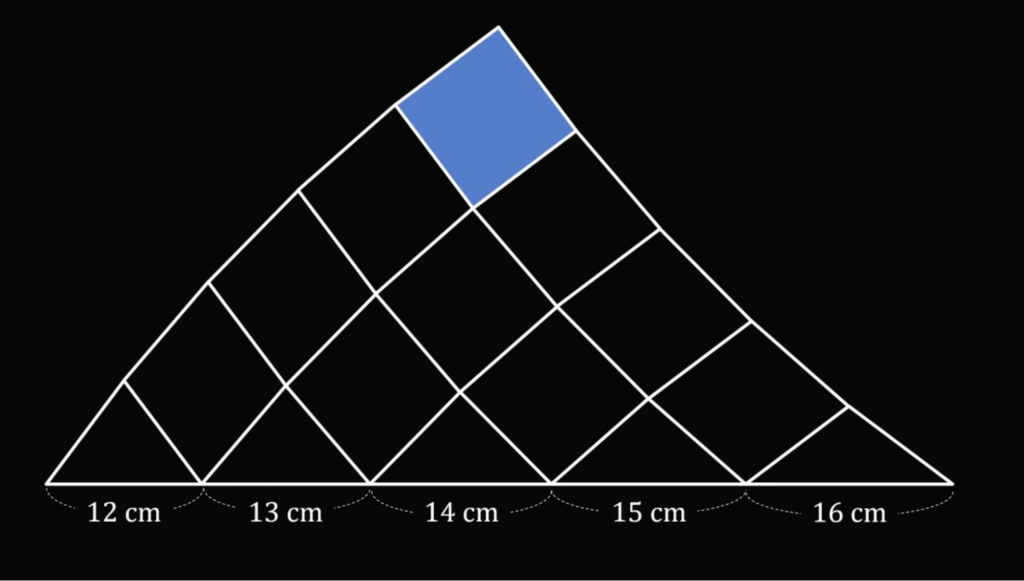
Может показаться, что сейчас нужно будет вычислять много геометрических штук и всё такое, но на самом деле всё сильно проще, следите за руками.
Так как наверху квадрат, то все его стороны равны, а между двумя соседними сторонами — 90 градусов:
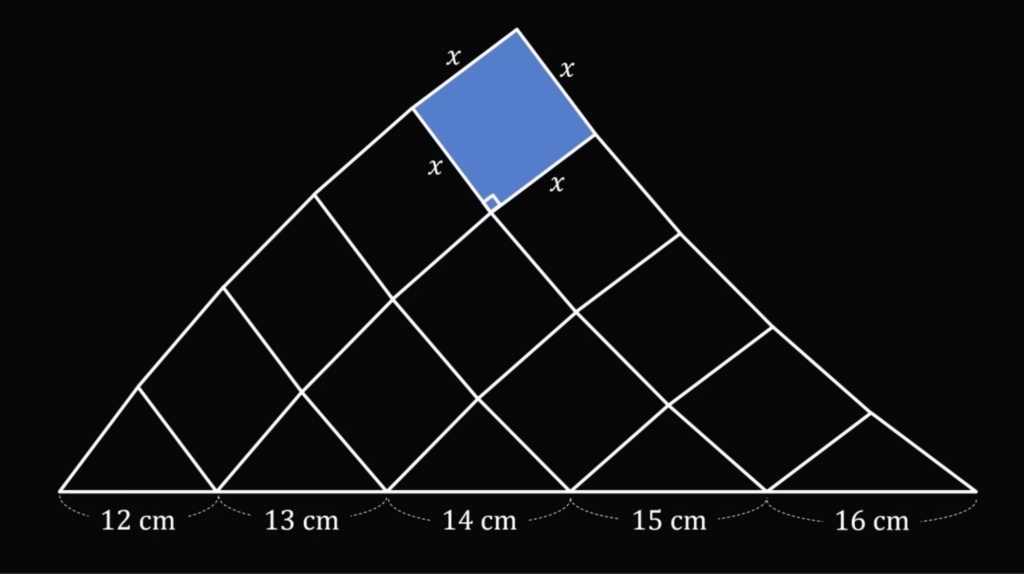
Теперь самое интересное: у нас от треугольников наверх всегда идут ромбы. На всякий случай напомним про их свойство, оно нам сейчас пригодится:
ромб — это параллелограмм (проще говоря, четырёхугольник), у которого все стороны равны.
Это значит, что длина стороны квадрата Х — это такая же длина, как и в треугольниках по 12 и 16 сантиметров. Вот как это выглядит для левого треугольника:
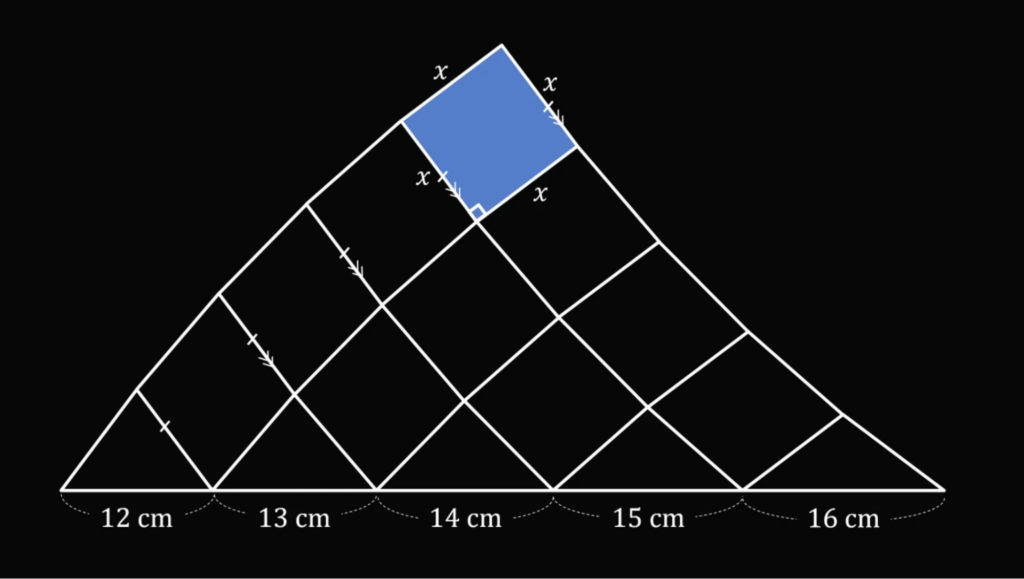
И так как справа тоже ромбы, то и для правого треугольника длина его стороны совпадает с длиной квадрата наверху:
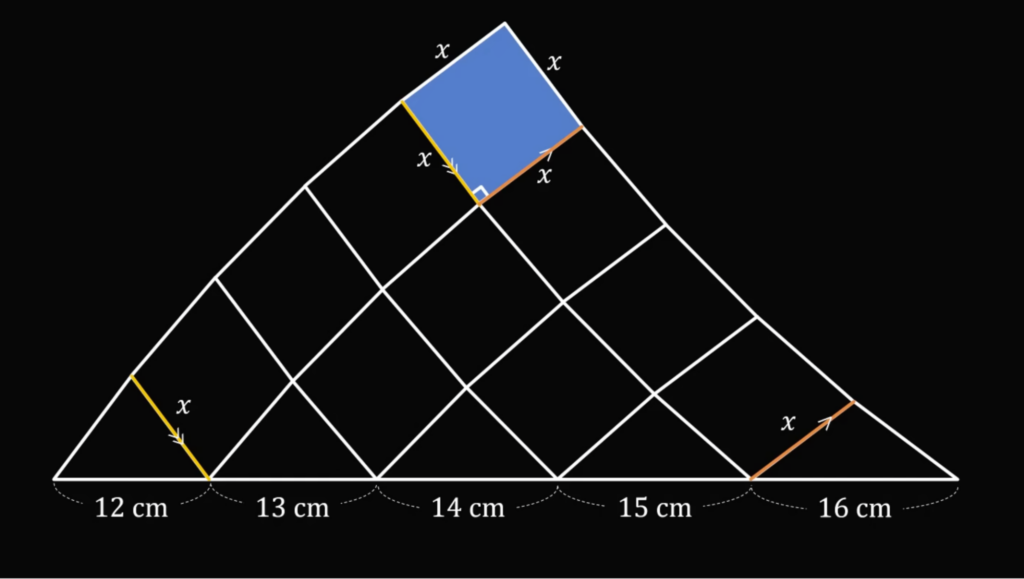
Получается, что если убрать всё, кроме этих трёх фигур, то будет видно, что стороны треугольников параллельны сторонам верхнего квадрата (потому что ромбы):
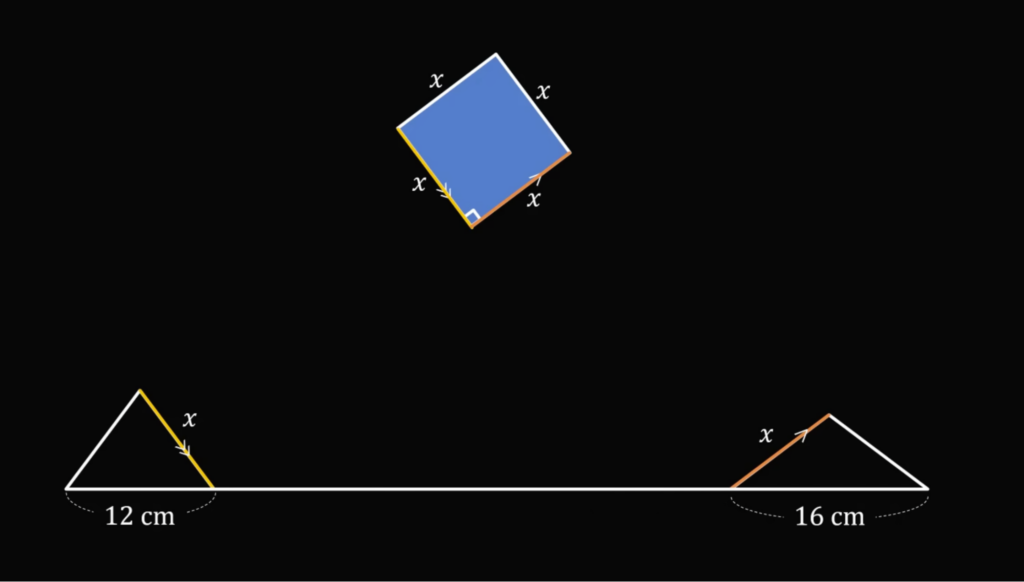
А это значит, что если поставить эти два треугольника рядом, то между соседними боковыми сторонами будет ровно 90 градусов:
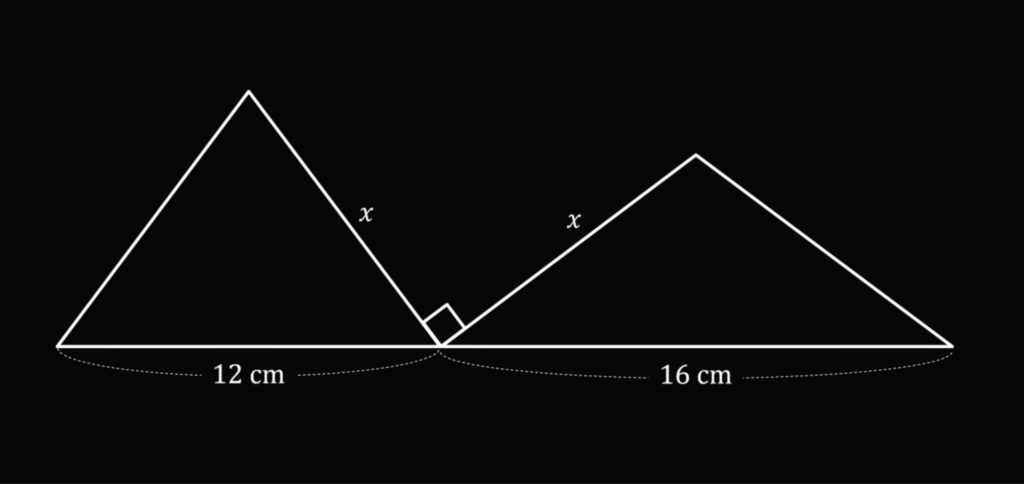
Теперь проведём высоту в каждом из них и вспомним, что высота в равнобедренном треугольнике делит основание ровно пополам:
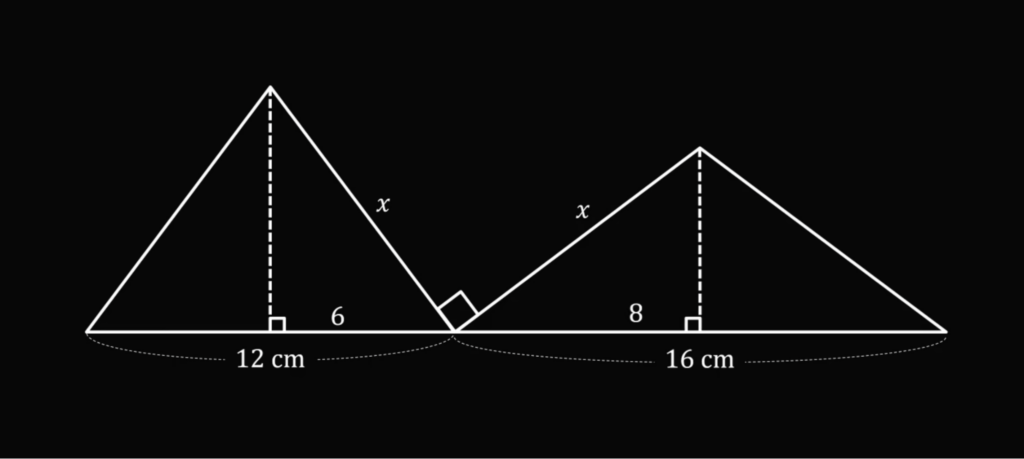
А дальше хитрое: так как у нас есть уже угол в 90 градусов, то два оставшихся угла в сумме тоже дают 90:
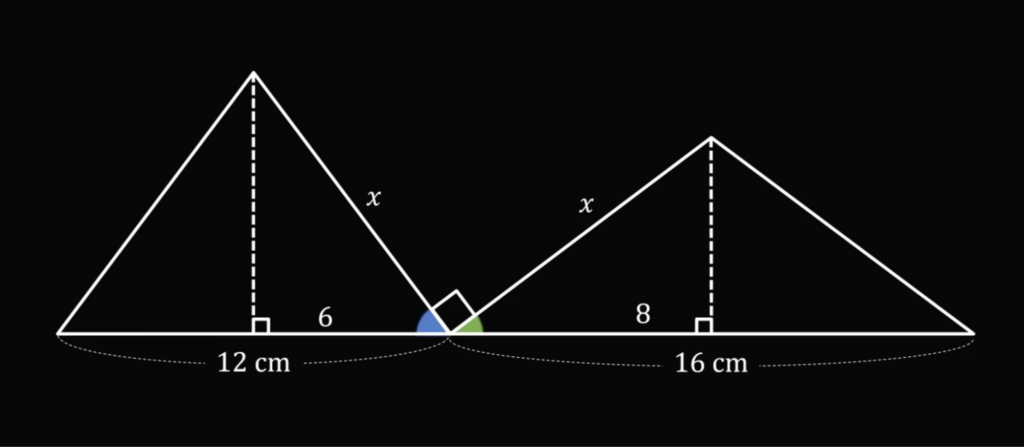
И раз, например, в правой половине левого треугольника уже есть один угол 90 градусов, то два других тоже дают в сумме 90. Это значит, что верхний угол правой половины левого треугольника равен зелёному углу правого (и наоборот — для правого):
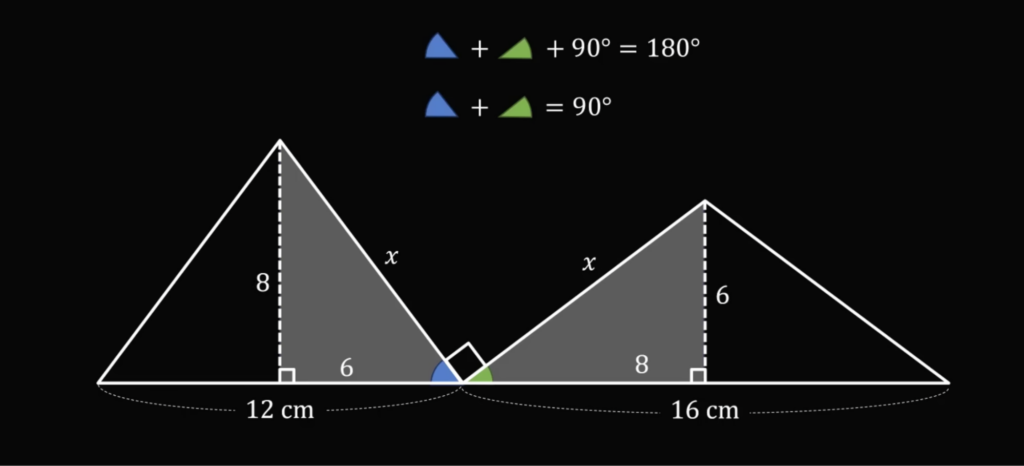
А раз так, то это одинаковые треугольники (потому что у них одинаковая гипотенуза — Х)!
Но если это одинаковые треугольники, то мы легко можем найти значения катетов: они просто поменяются местами — 6 и 8 сантиметров соответственно (смотрите на рисунок выше).
Теперь вспомним единственную сложную формулу в этой задаче — квадрат гипотенузы равен сумме квадратов катетов:
Х² = 6² + 8² = 36 + 64 = 100
Но Х² — это же как раз площадь нашего квадрата наверху! Получается, мы только что решили задачу и нашли площадь квадрата — 100 квадратных сантиметров.
Уф. Было интересно :-)
Задача для хакеров: как подобрать код к замку
Дьявольская загадка про книжного червя
Интересная задача на логику про ключи и пессимиста
Безумная задача про лапшу из собеседования, которую можно решить без сложной математики
Задача про внутренние ощущения и безжалостную математику
Три задачи про переливания, с которыми может справиться каждый (но не всегда)Бонус для читателей
Если вам интересно погрузиться в мир ИТ и при этом немного сэкономить, держите наш промокод на курсы Практикума. Он даст вам скидку при оплате, поможет с льготной ипотекой и даст безлимит на маркетплейсах. Ладно, окей, это просто скидка, без остального, но хорошая.
Вам слово
Приходите к нам в соцсети поделиться своим мнением о задаче и почитать, что пишут другие. А ещё там выходит дополнительный контент, которого нет на сайте — шпаргалки, опросы и разная дурка. В общем, вот тележка, вот ВК — велком!
