Отряд ниндзя незаметно подобрался к городу на расстояние 30 км. В городе нет ни электричества, ни связи.
Захватчиков случайно замечает городской сторож. Он решается на марш-бросок по параллельной дороге, чтобы предупредить городские власти.
Прибыв в город, сторож докладывает о ситуации и получает приказ: бежать обратно, посмотреть расположение отряда ниндзя и снова доложить о ситуации. Так нужно бегать до тех пор, пока ниндзя вплотную не подойдут к городу.
Отряд ниндзя передвигался со скоростью 4 км/ч. Сторож, не жалея себя, всю дистанцию бегал со скоростью 6 км/ч — его усилия оправдались и атака была отбита.
👉 Вопрос: сколько километров пробежал сторож, пока он бегал туда-сюда?
Подсказка
Начните рассуждение с простого рисунка, на котором схематически изобразите расположение участников и порядок их перемещения по отношению друг к другу. После соберите доступные данные и попробуйте их привязать к известной математической закономерности.
Отряд ниндзя и сторож находились в постоянном движении, меняя расстояние между городом и друг другом. Чтобы ничего не упустить, будем схематически отображать перемещения сторон и параллельно делать расчёты.
Шаг №1. Отряд ниндзя и сторож находятся в 30 км от города — это исходная точка, с которой начинается расчёт. Сторож замечает захватчиков и со скоростью 6 км/ч направляется к городу — так он пробегает первые 30 км.
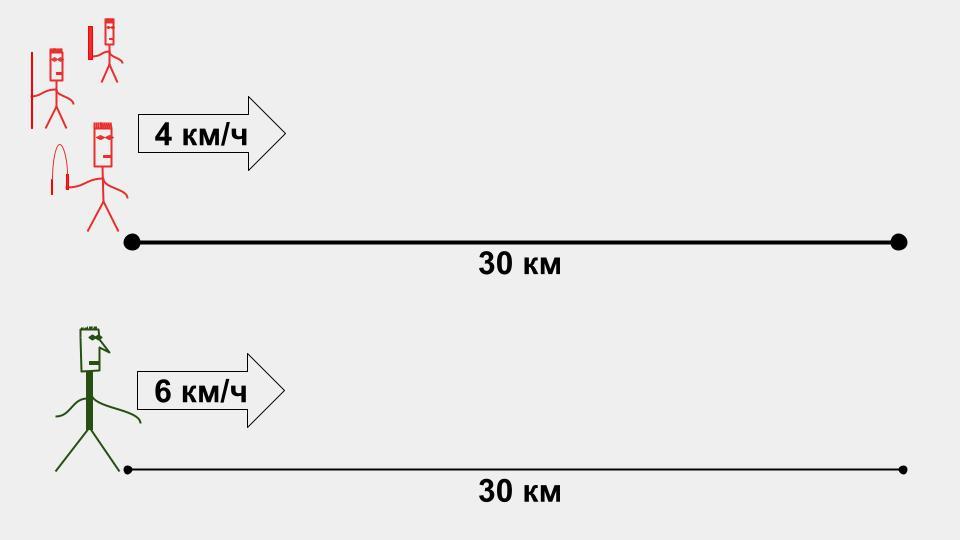
Шаг №2. Сторож бежит с постоянной скоростью, и поэтому мы можем узнать, за какое время он преодолеет всю дистанцию. Делим расстояние на скорость:
30 км ÷ 6 км/ч = 5 часов
За 5 часов сторож добегает до города и докладывает об отряде ниндзя.
Шаг №3. Нам известно, что отряд ниндзя двигается со скоростью 4 км/ч и сколько времени сторож добирался до города. По этим данным можно посчитать, насколько ниндзя приблизились к городу, когда сторож доложил об атаке:
4 км/ч × 5 ч = 20 км
Когда сторож закончил первый марш-бросок, ниндзя прошли большую часть пути и приблизились к городу на 20 км. Осталось преодолеть 10 км.
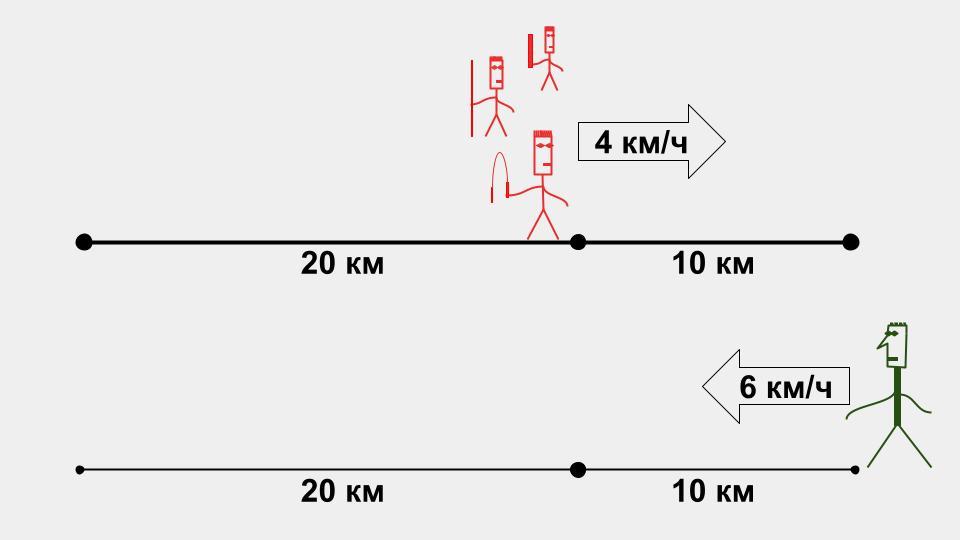
Шаг №4. Через 5 часов сторож отправляется на второй марш-бросок: из города к расположению отряда ниндзя. Стороны двигаются навстречу друг другу, и поэтому мы можем рассчитать скорость сближения и время встречи в одной точке:
6 км/ч + 4 км/ч = 10 км/час — скорость сближения сторон
10 км/ч ÷ 10 км = 1 час — время встречи в одной точке
После встречи с отрядом ниндзя сторож развернулся и сразу побежал обратно в город: один час он бежал в одну сторону и ещё один час — в другую.
2 ч × 6 км/ч = 12 км
Ниндзя за два часа прошли 8 км и до города им оставалось 2 км.
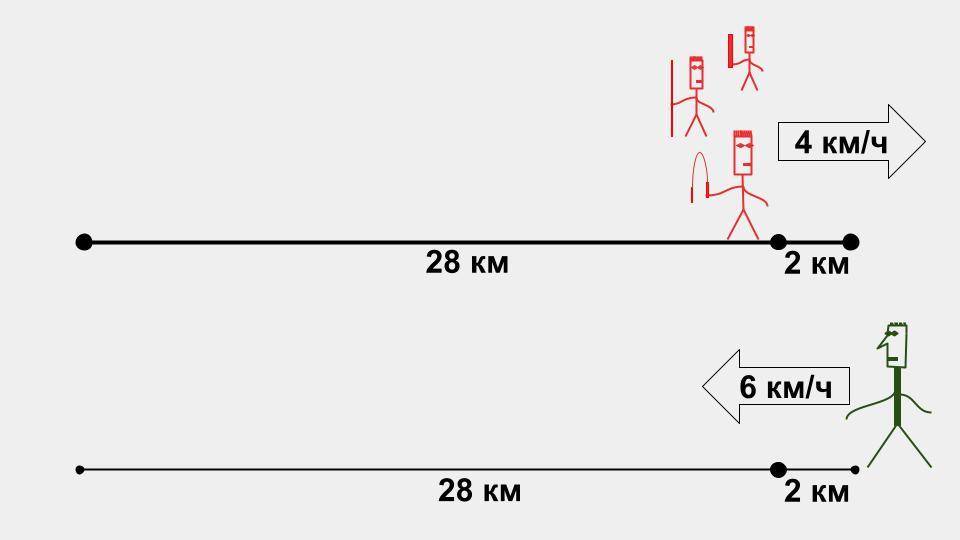
Шаг №5. Сторож разворачивается, и стороны опять движутся навстречу со скоростью сближения 10 км/ч. Считаем время, которое понадобится для встречи:
2 км ÷ 10 км/час = 0,2 часа
Теперь считаем расстояние, которое пробежит сторож:
6 км/ч × 0,2 часа = 1,2 км
Когда это расстояние будет пройдено, сторож снова развернётся и побежит обратно. Так будет продолжаться до тех пор, пока ниндзя не дойдут до города.
Шаг №6. Делаем промежуточный расчёт расстояния, пройденного сторожем:
30 км + 6 км + 6 км + 1,2 км + 1,2 км и так далее
Замечаем, что расстояния образуют бесконечно убывающую геометрическую прогрессию со знаменателем 0,2 и первым членом 6, который повторяется дважды.
Для бесконечно убывающей геометрической прогрессии мы находим нужную формулу, подставляем известные числа и считаем:
S = b₁/(1 - q) — формула бесконечно убывающей геометрической прогрессии, где b₁= 6, а q = 0,2
Перед финальным расчётом не забываем учитывать, что члены геометрической прогрессии повторяются по два раза. Поэтому наша формула будет такой:
30 км + (2× (6/(1 - 0,2)) км = 30 км + 15 км = 45 км
Записываем ответ: за всё время сторож пробежит 45 км. Такие дела 😆😆😆