В прошлый раз мы наблюдали, как Санта-Клаус и Дед Мороз выясняли, кто из них круче, при помощи игры «камень-ножницы-бумага». На этот раз они решили узнать, что лучше — русская тройка лошадей Деда Мороза или упряжка с девятью оленями Санта-Клауса.
Санта-Клаус предложил устроить гонки на квадратном поле площадью 40 акров, на краю которого стояла одинокая ель. Санта-Клаус схитрил и настоял на таких условиях: стартовать они с Дедом Морозом будут из разных вершин, а финиш будет на одной. При этом Санта-Клаус начнёт от вершины A, а Дед Мороз должен ехать от вершины B сначала к ели в 110 ярдах от финиша, а затем к вершине D.
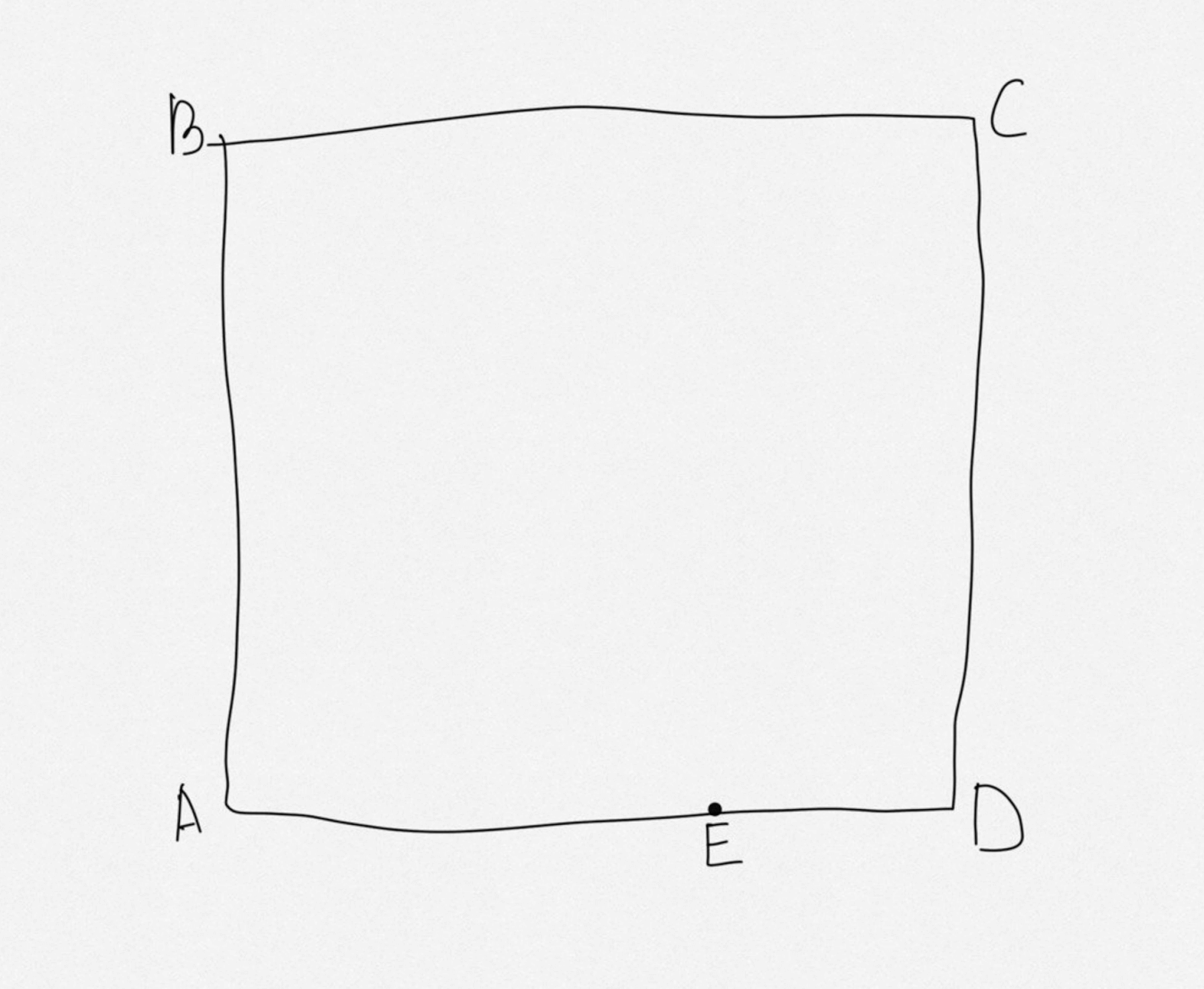
Чтобы получить преимущество, Санта-Клаус предложил использовать американскую систему счисления с акрами и ярдами — так ему будет проще всё считать, а Деду Морозу — сложнее. Когда Дед Мороз доехал до ели, Санта-Клаус понял, что опережает его на 30 ярдов. Кто пришёл к финишу первым и на сколько обогнал другого?
Для начала выясним, какие у нас данные по условию. В 1 акре 4840 квадратных ярдов, значит, квадратное поле площадью 40 акров =
S = 4840 × 40 = это 193600 квадратных ярдов
Извлечём из этого числа квадратный корень, чтобы получить длину каждой стороны поля:
AD = √193600 = 440 ярдов
Теперь посчитаем, в какой точке Е находится одинокая ель. Поскольку она расположена в 110 ярдах от финиша, то расстояние AE получается таким:
AE = AD − ED = 440 − 110 = 330 ярдов
Вычислим, какое расстояние d проехал Дед Мороз, прежде чем поравняться с Санта-Клаусом. Поскольку получается, что Дед Мороз ехал по гипотенузе прямоугольного треугольника ABE, то теореме Пифагора квадрат её длины BE равен сумме квадратов сторон AD и AE:
d2 = AD2 + AE2 = 4402 + 3302 = 302500
Осталось извлечь квадратный корень из суммы — и мы получим путь Деда Мороза до точки E:
d = √302500 = 550 ярдов
Теперь рассчитаем, с какой скоростью двигались тройка лошадей Деда Мороза и девять оленей Санта-Клауса. Возьмём первую за x, а вторую — за y. Поскольку когда Дед Мороз доехал до одинокой ели, Санта-Клаус опережал его на 30 ярдов, получается, что Санта-Клаус проехал ED + 30:
AE + 30 = 360 ярдов
Отношение расстояний пропорционально отношению скоростей. Возьмём скорость Санта-Клауса за s, а скорость Деда Мороза — за c:
360/550 = s/c
Скорости Санта-Клауса и Деда Мороза составляет 33k и 55k соответственно, где k — какое-то число больше 0.
Санта-Клаус преодолеет оставшееся до финиша расстояние в 440 − 360 = 80 ярдов за 2,2/k единиц времени, а Дед Мороз оставшиеся 110 ярдов — за 2/k единиц времени.
Поскольку Деду Морозу требуется меньше времени, чем Санта-Клаусу, Дед Мороз выигрывает гонку.
Теперь посчитаем, на сколько Дед Мороз в итоге обогнал Санта-Клауса.
Запас дистанции = (55 × 2) − (36 × 2 + 30) = 8 ярдов.
Получается, что Дед Мороз выигрывает гонку с преимуществом 8 ярдов. А по-русски — он обогнал Санта-Клауса на 7,28 метра.