Как автомобильный навигатор находит самый быстрый путь

Когда вы пользуетесь навигатором, вы указываете точку А и точку Б, и дальше навигатор как-то сам строит маршрут. Сегодня посмотрим, что лежит в основе алгоритма, который это делает. Просто ради интереса. 

Графы и «задача коммивояжёра»

Ещё до появления навигаторов у людей была такая же проблема: как найти кратчайший путь из одного места в другое, если есть ограниченное количество промежуточных точек? Или как объехать ограниченное количество точек, затратив минимальные усилия. В общем виде это называется «задачей коммивояжёра», и мы уже рассказывали, в чём там идея:

Если взять просто города и расстояния между ними, то с точки зрения математики это называется графом: города будут вершинами графа, а дороги между ними — рёбрами графа. Если мы знаем длину каждой дороги, то это будет значением (весом) рёбер графа. Этой теории нам уже хватит, чтобы понять, как работает навигатор в машине.

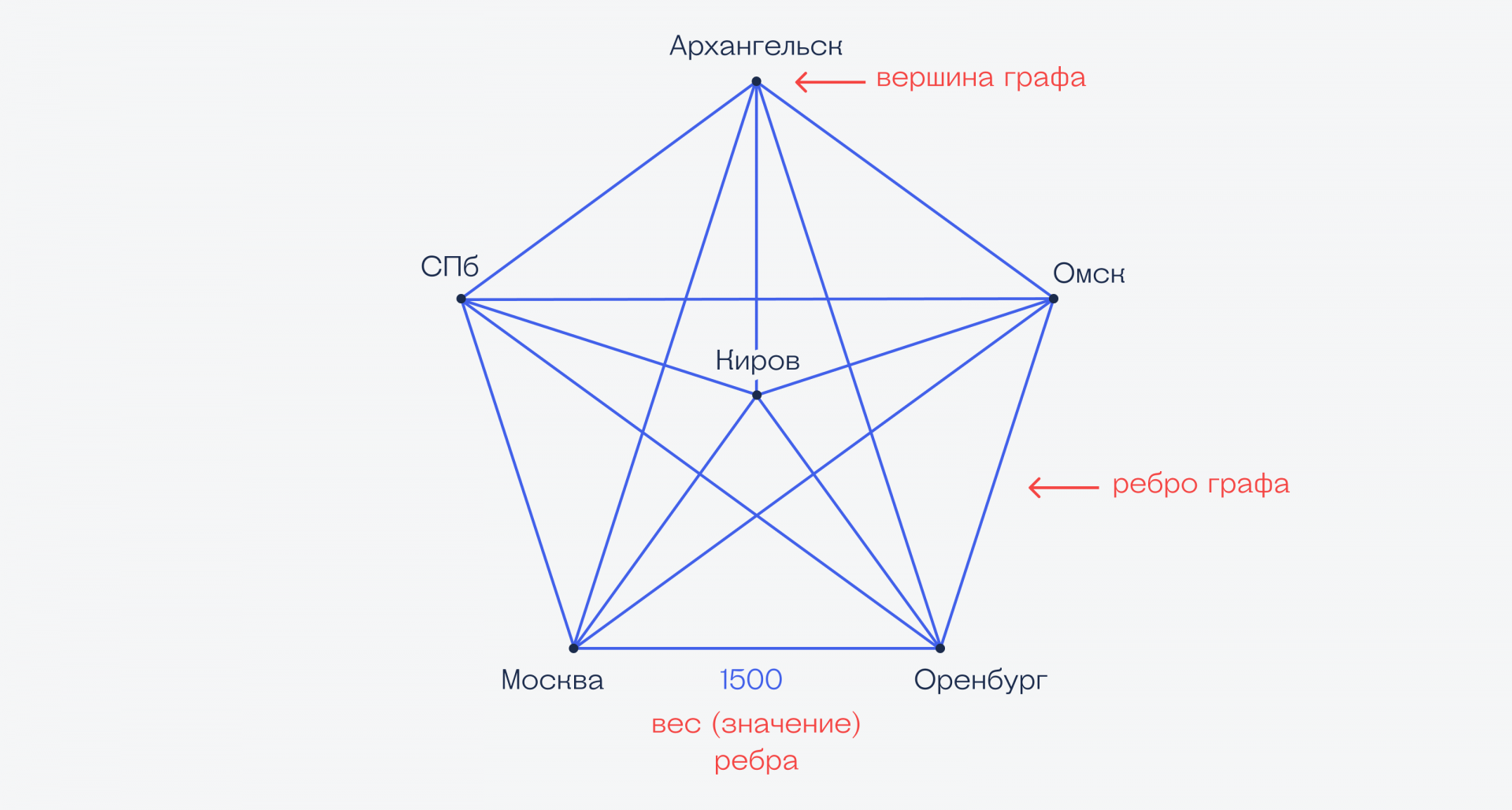
Алгоритм Дейкстры — ищем самый быстрый путь

Как только появилось решение полным перебором, математики стали искать другой подход, который работал бы гораздо быстрее и не требовал бы вычисления такого огромного объёма данных. В 1959 году Эдсгер Дейкстра придумал свой алгоритм, которым пользуются до сих пор. Идея его в том, чтобы не перебирать все варианты, а находить самый короткий путь только между соседними графами — и так, шаг за шагом, продвигаться к конечной точке.

Допустим, у нас есть улицы, перекрёстки и мы знаем время пути между ними. Нарисуем это в виде графа, а чтобы было проще ориентироваться — сделаем визуально всё одинаковой длины:

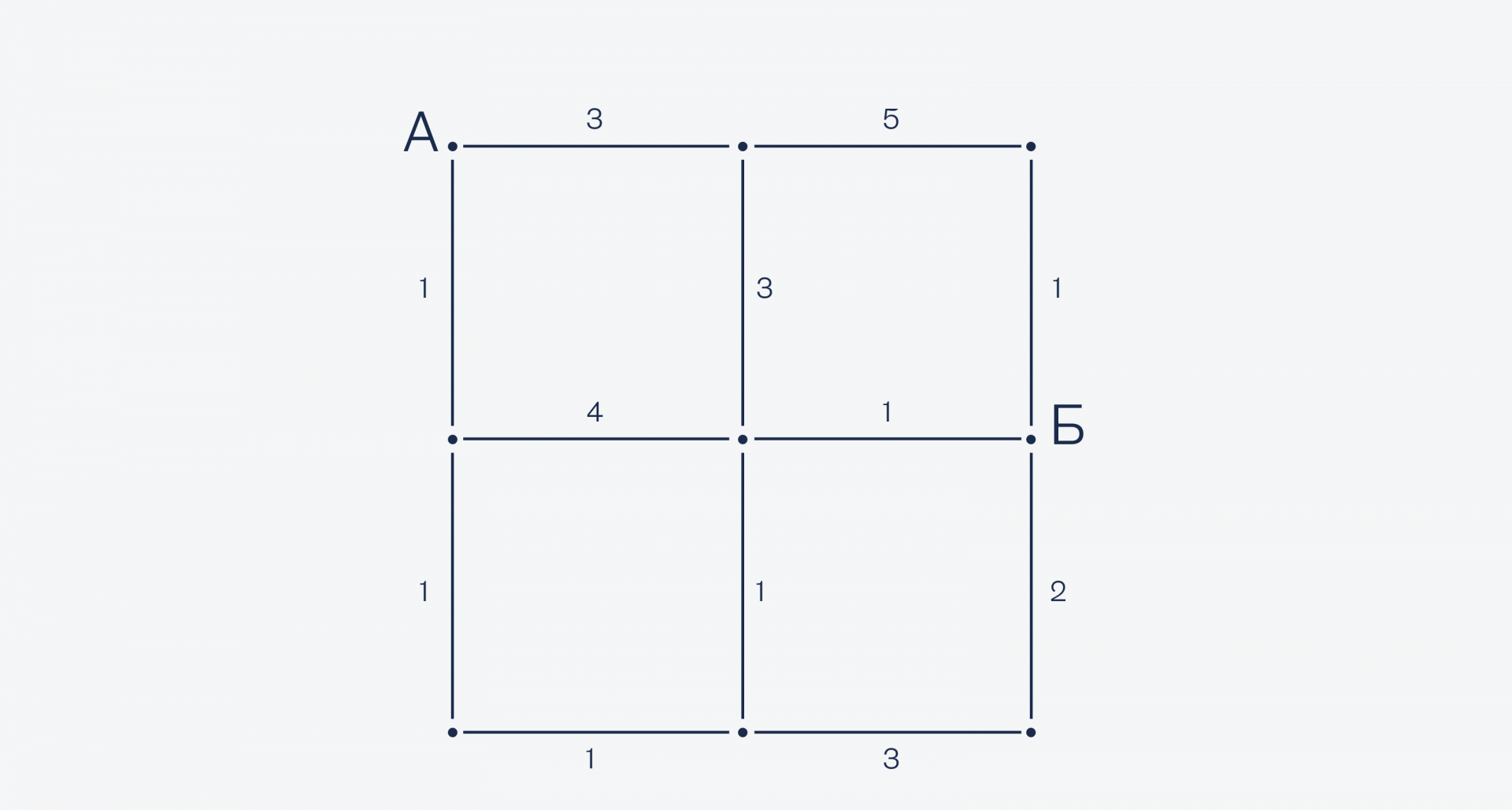
Чтобы найти самый быстрый путь из А в Б, мы смотрим сначала, какие пути у нас выходят из точки А. Видно, что поехать вниз будет быстрее, чем поехать направо:

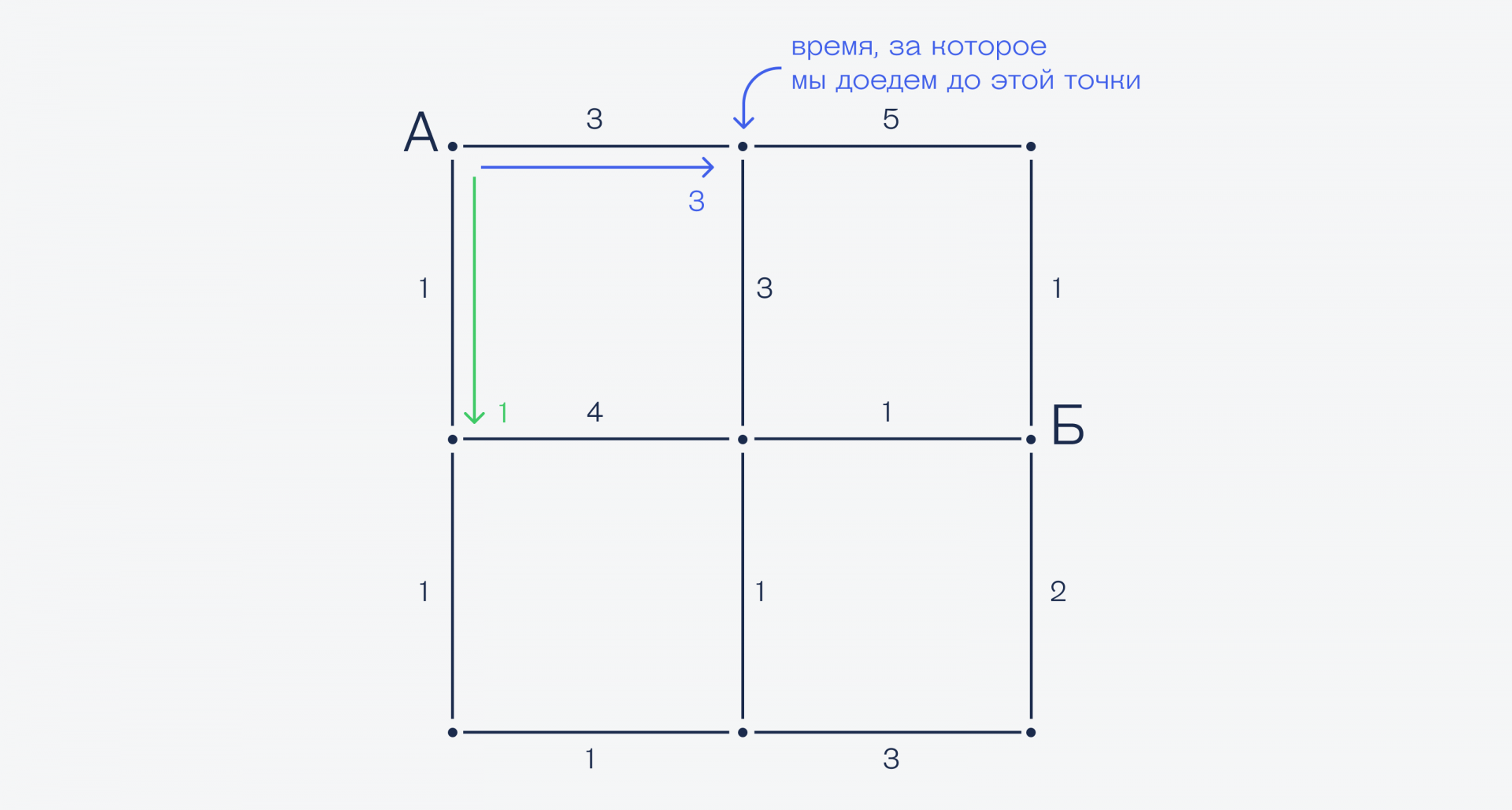
Значит, выбираем путь вниз. Теперь делаем то же самое для этой точки — смотрим, где быстрее: справа или внизу. Вниз быстрее (1 меньше, чем 4), поэтому едем по ней:

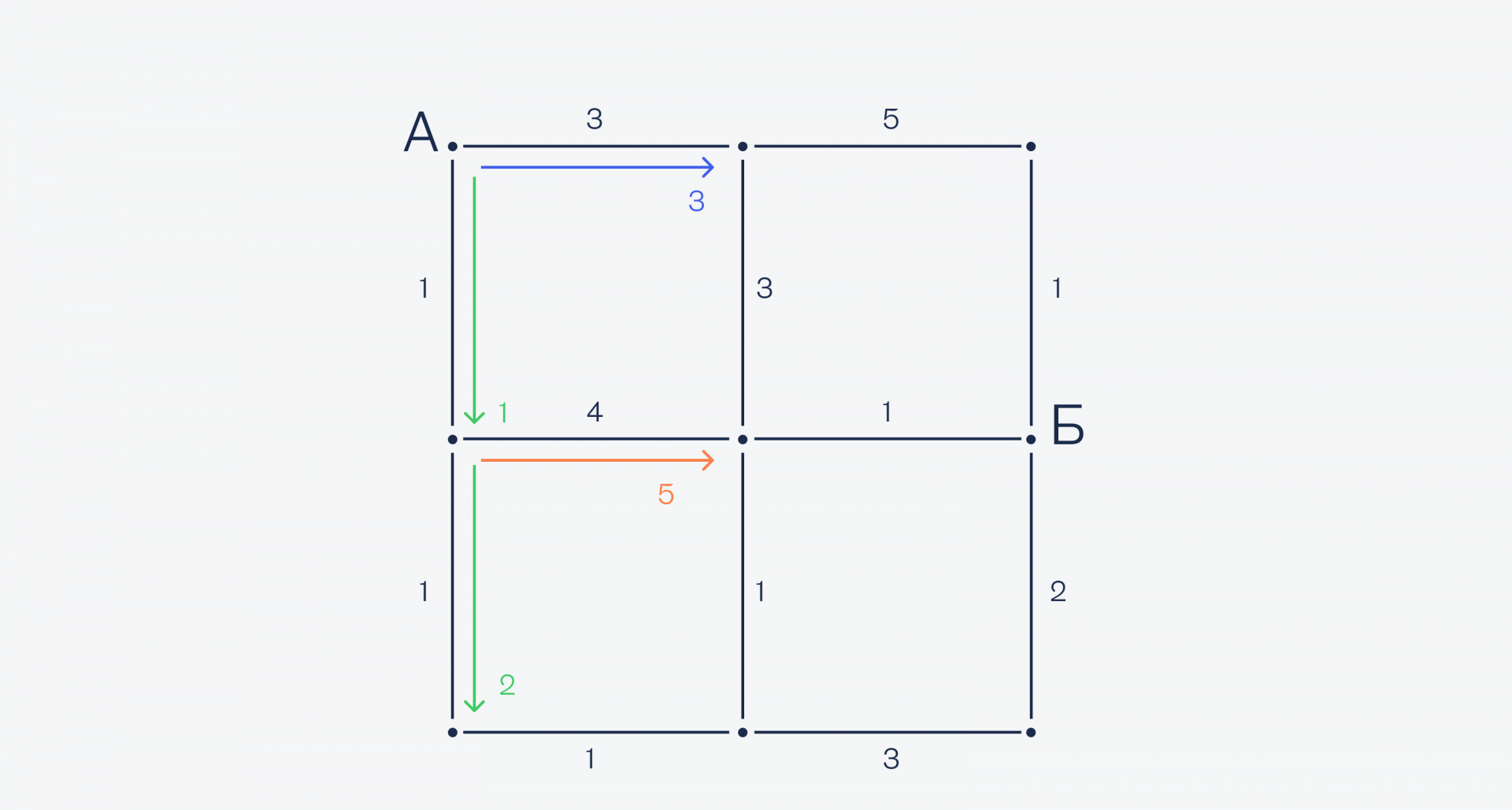
При этом мы не отбрасываем уже сделанные вычисления (всё равно уже посчитали), а запоминаем их на всякий случай. Из нижней точки есть только одна дорога — направо, поэтому едем по ней:

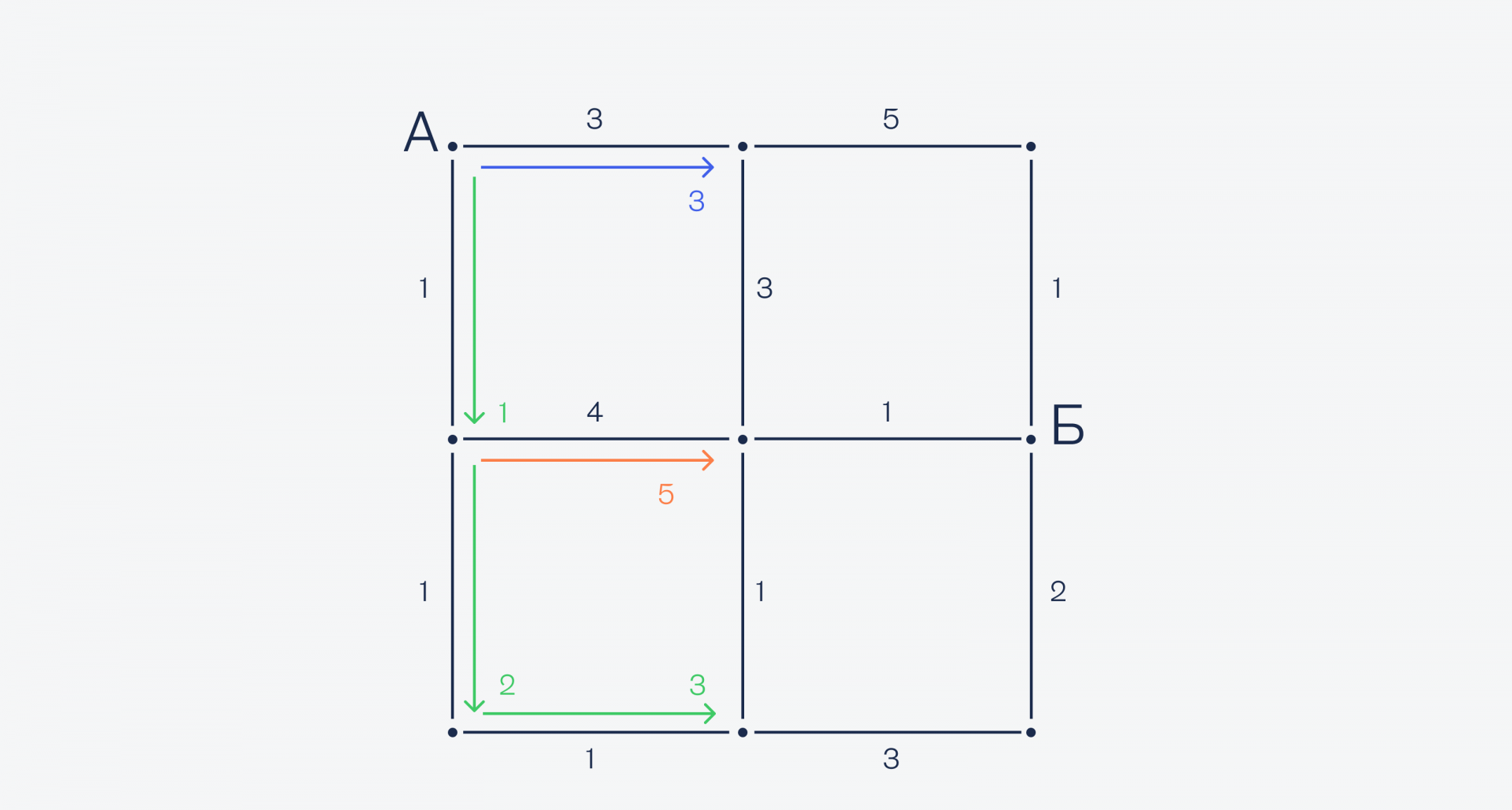
А теперь у нас получилась интересная ситуация: в центральную точку мы можем попасть как сверху, так и снизу, при этом и там, и там у нас одинаковое время — 3 минуты. Значит, посчитаем оба варианта — вдруг сверху будет быстрее и нам нужно будет перестроить маршрут заново:

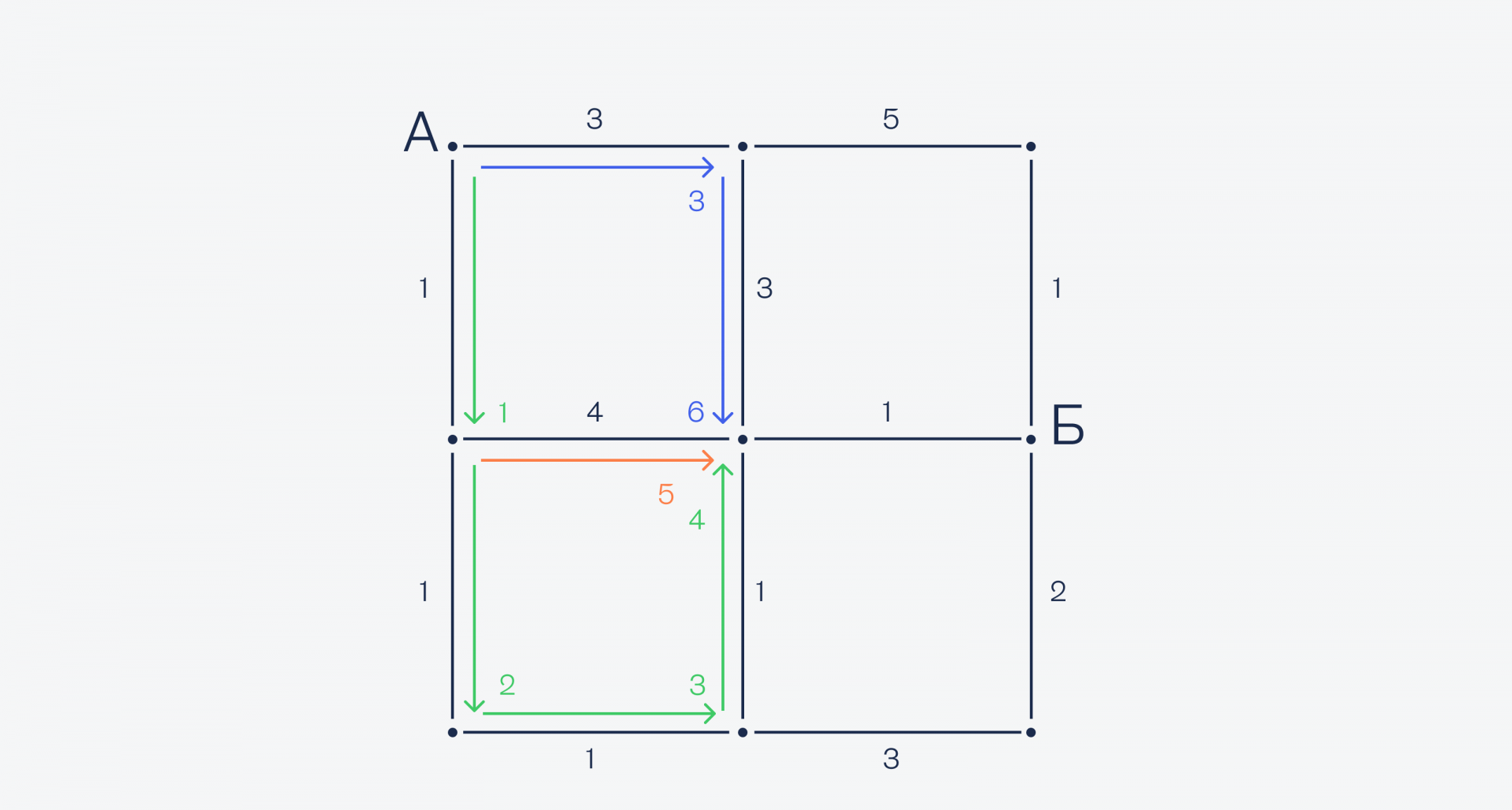
Оказывается, снизу ехать до центра быстрее, чем сверху — 4 минуты вместо 6, поэтому оставляем нижний маршрут. Наконец, из центральной точки до точки Б всего один путь — направо, поэтому выбираем его:

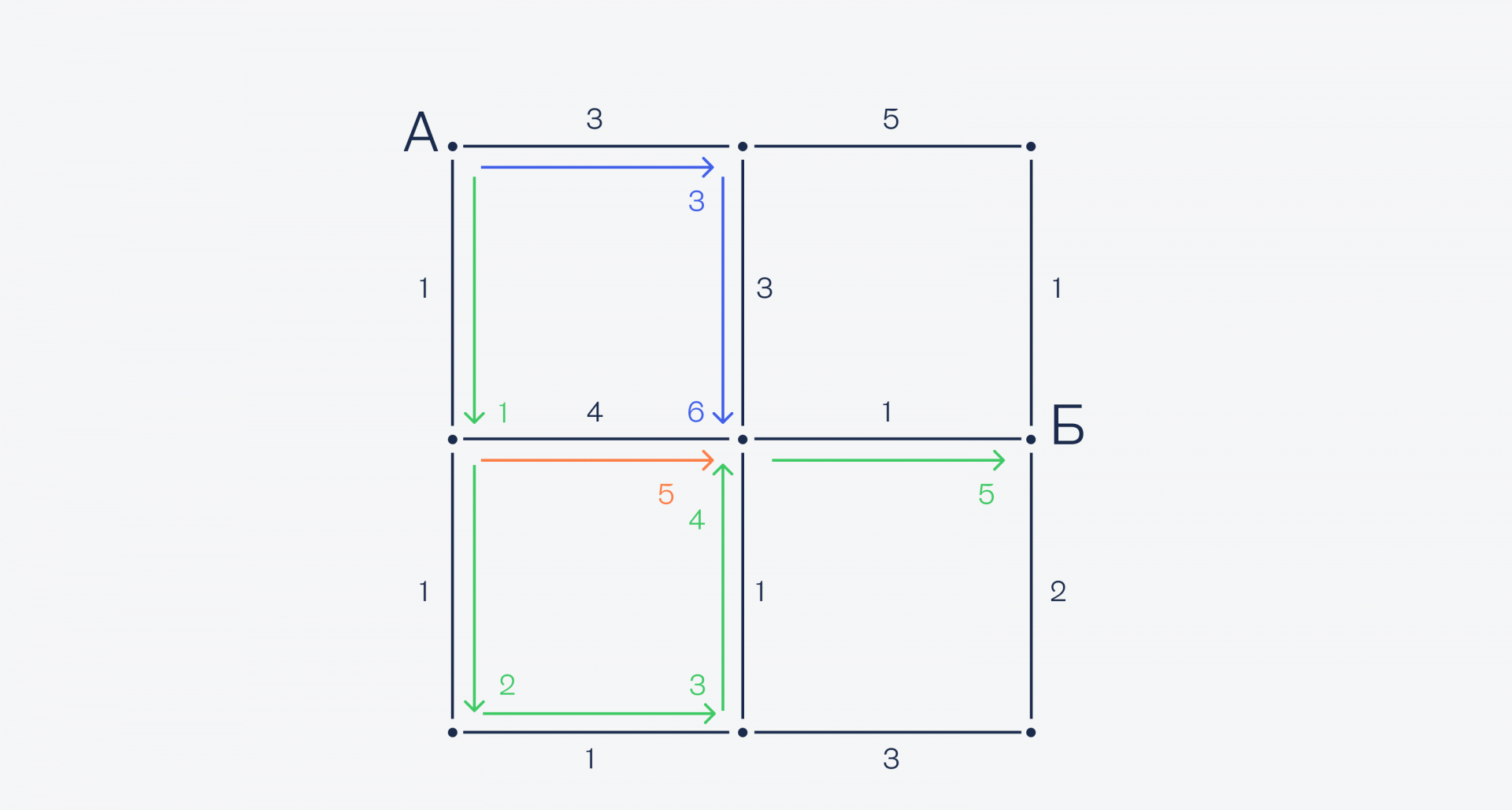
Как видите, нам не пришлось считать все варианты со всеми точками, а до некоторых мы просто не добрались. Это сильно сэкономило время и потребовало меньше ресурсов для вычисления.Такой алгоритм и лежит в основе автомобильных навигаторов — с вычислениями справится даже бюджетный смартфон.

Что ещё учитывает навигатор

Чтобы алгоритм оставался простым и работал только со временем, все остальные параметры дорог тоже привязывают ко времени. Покажем, как это работает, на паре примеров.

Комфорт. Если нам нужно построить не самый быстрый, а самый комфортный маршрут, то мы можем отдать предпочтение автомагистралям и дорогам с несколькими полосами — на них обычно и асфальт получше, и резких поворотов поменьше. Чтобы навигатор выбирал именно такие дороги, им можно присвоить коэффициент 0,8 — это виртуально сократит время на дорогу по ним на 20%, а навигатор всегда выберет то, что быстрее. 

С просёлочными и грунтовыми дорогами ситуация обратная. Они редко бывают комфортными, а значит, им можно дать коэффициент 1,3, чтобы они казались алгоритму более долгими и он старался их избегать. А лесным дорогам можно поставить коэффициент 5 — навигатор их выберет, только если это единственная дорога то точки назначения.

Сложность маршрута и реальное время. Маршрут из А в Б почти никогда не бывает прямым — на нём всегда есть повороты, развороты и съезды, которые отнимают время. Чтобы навигатор это учитывал, в графы добавляют время прохождения поворота — либо коэффициентом, либо отдельным параметром. Из-за этого алгоритм будет искать действительно быстрый маршрут с учётом геометрии дорог.

Пробки. Если есть интернет, то всё просто: навигатор получает данные о состоянии дорог и добавляет разные коэффициенты в зависимости от загруженности. Иногда навигатор ведёт дворами, когда трасса свободна — это не ошибка навигатора, а его прогноз на время поездки: если через 10 минут в этом месте обычно собираются пробки, то там лучше не ехать, а заранее поехать в объезд.

Если интернета нет, то алгоритм просто использует усреднённую модель пробок на этом участке. Эта модель скачивается заранее и постоянно обновляется в фоновом режиме.

Как построить маршрут по всей России

Если нам нужно построить маршрут из Брянска в Тулу, то с точки зрения компьютера это безумно сложная задача: ему нужно перебрать десятки тысяч улиц и миллионы перекрёстков, чтобы понять, какой путь выбрать. С этим плохо справляется даже обычный компьютер, не говоря уже о телефоне.

Если мы в Яндекс Картах построим такой маршрут, то навигатор нам предложит сразу 4 варианта:

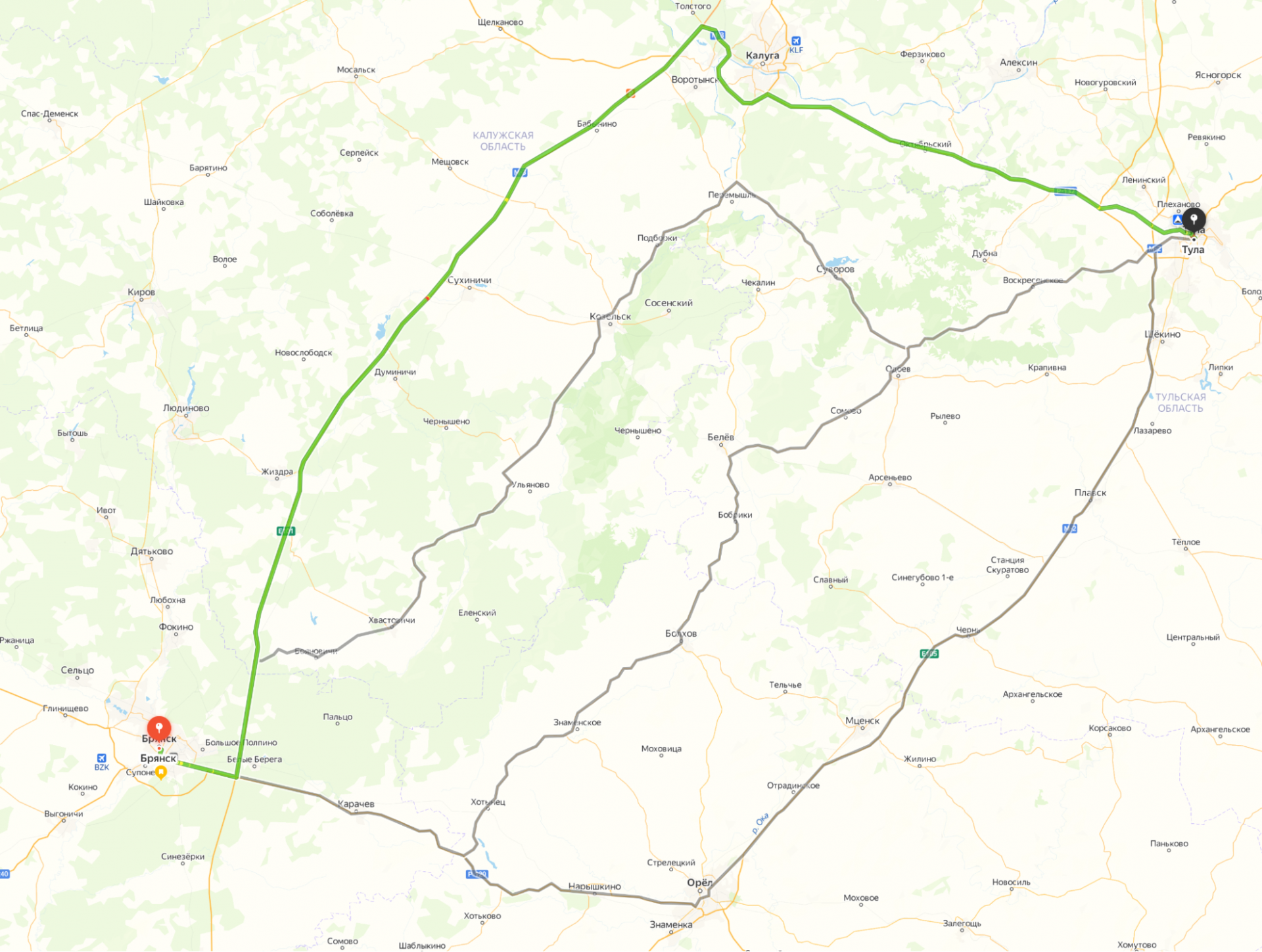
Но мы не ждали полчаса, пока сервер на той стороне посчитает все перекрёстки, а получили результат через пару секунд. Хитрость в том, что алгоритм использует уже заранее просчитанные варианты маршрутов и подставляет их для ускорения.

Например, если мы поедем в Тулу не из Брянска, а из Синезёрок, то поменяется только начальный маршрут по трассе М3, а всё остальное останется прежним:

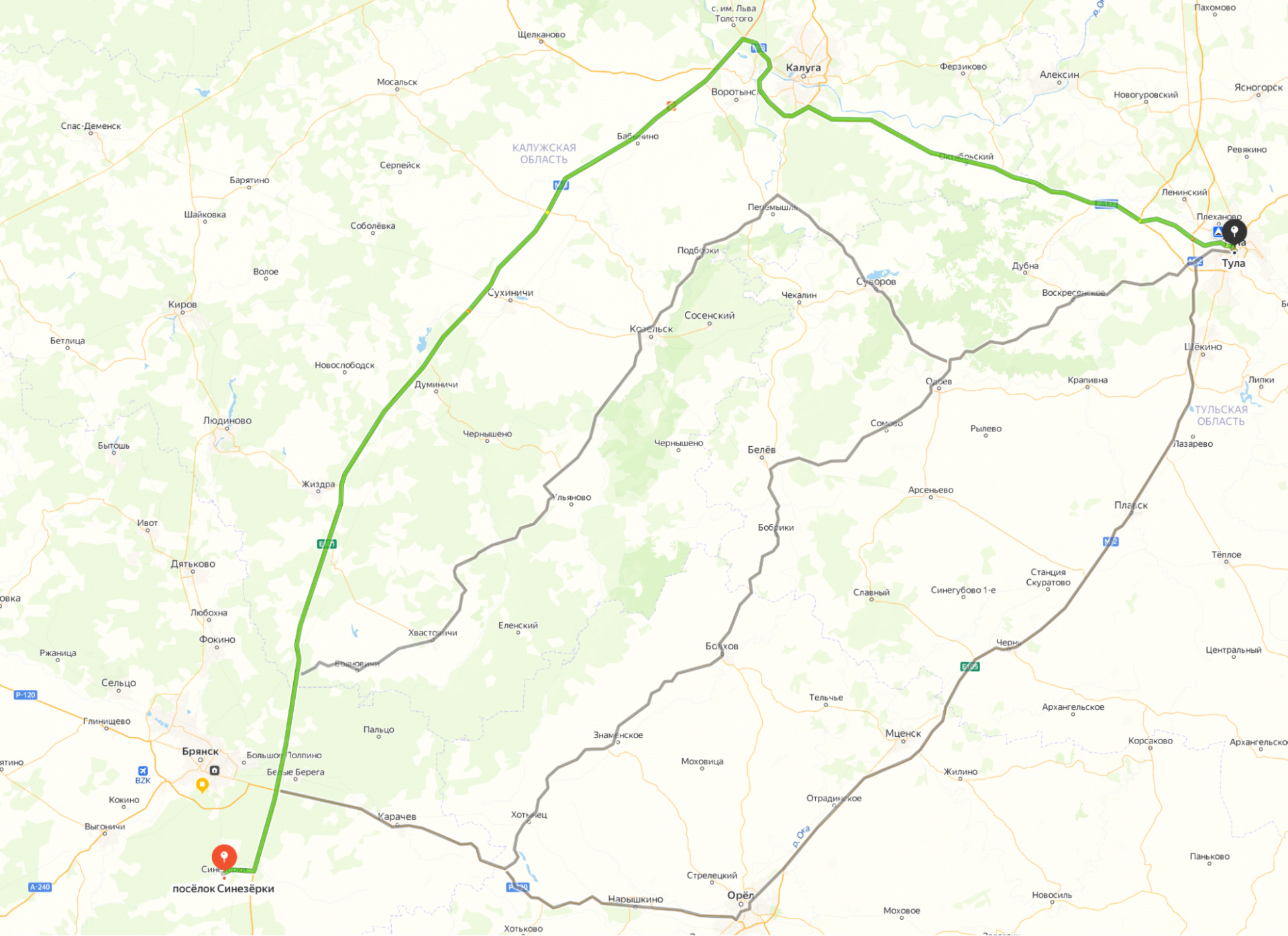
Получается, что навигатору не нужно всё пересчитывать — он находит только ключевые точки пути, а маршрут между ними уже просчитан до этого. Этот приём работает и при перестроении маршрута во время движения: навигатор смотрит, как нужно поменять путь, чтобы вернуть вас на уже известную дорогу.

Что дальше

Следующий этап — напишем алгоритм Дейкстры сами и посмотрим, как он работает по шагам.