Сегодня — две задачи с собеседований на позиции в бигдате, машинном обучении и нейросетях. Для работы там нужно знать математику и находить хитрые пути решения. Обе задачи как раз из таких.
Очень простая задача. Найти, чему равен X в этом уравнении:
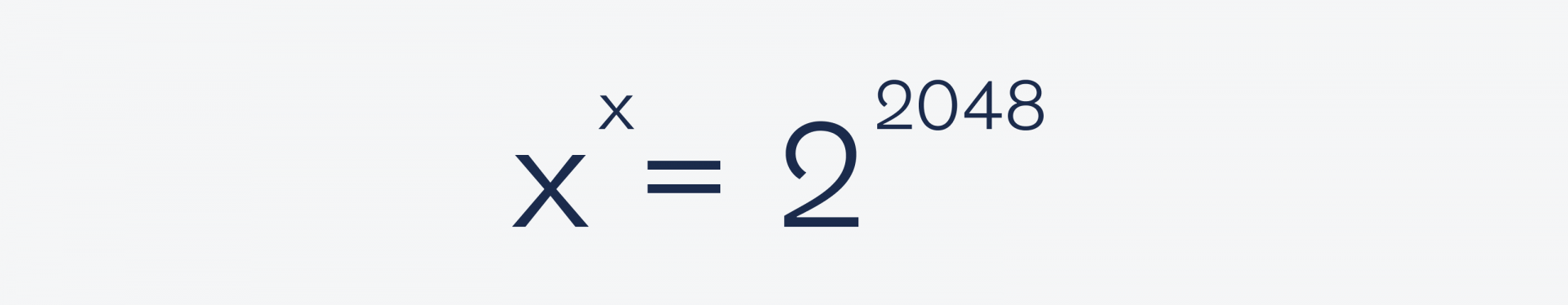
Несмотря на мнимую сложность и степени, эта задача решается за минуту. Всё, что нам понадобится, — это известное ещё со школы свойство перемножения степеней, которое работает так:
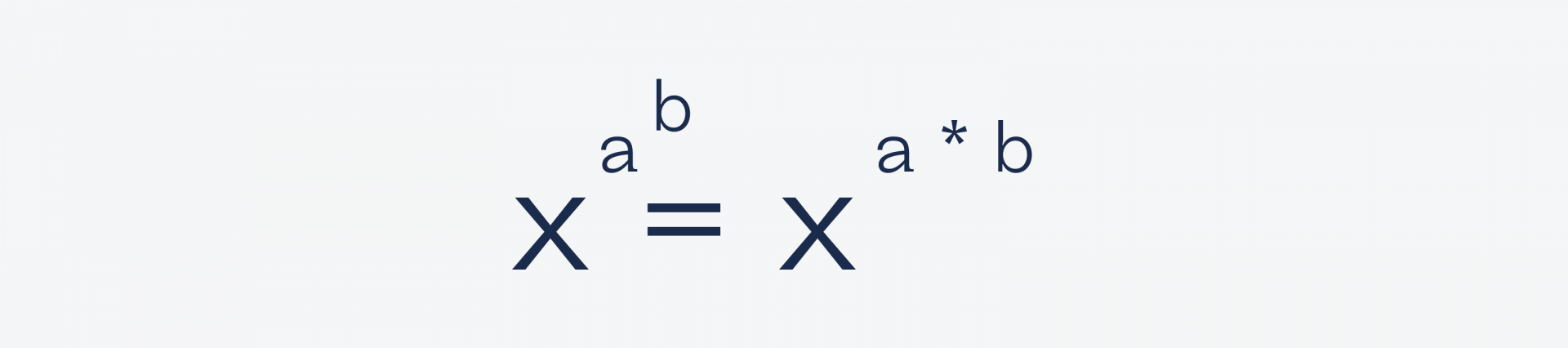
Теперь используем это, чтобы сравнять основание и степень в левой части:
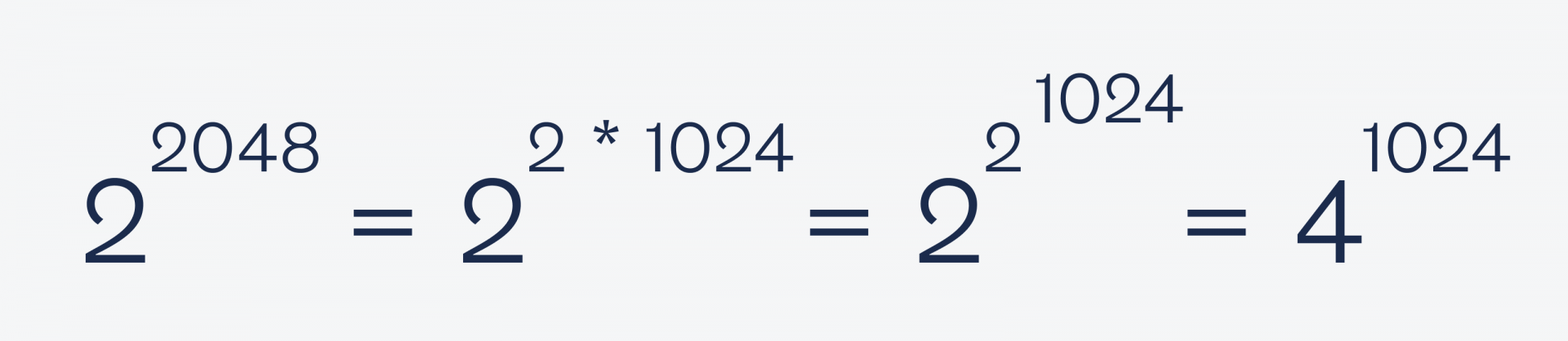
Дальше так же выносим двойку из каждой степени и возводим в неё основание, пока числа не станут равны:
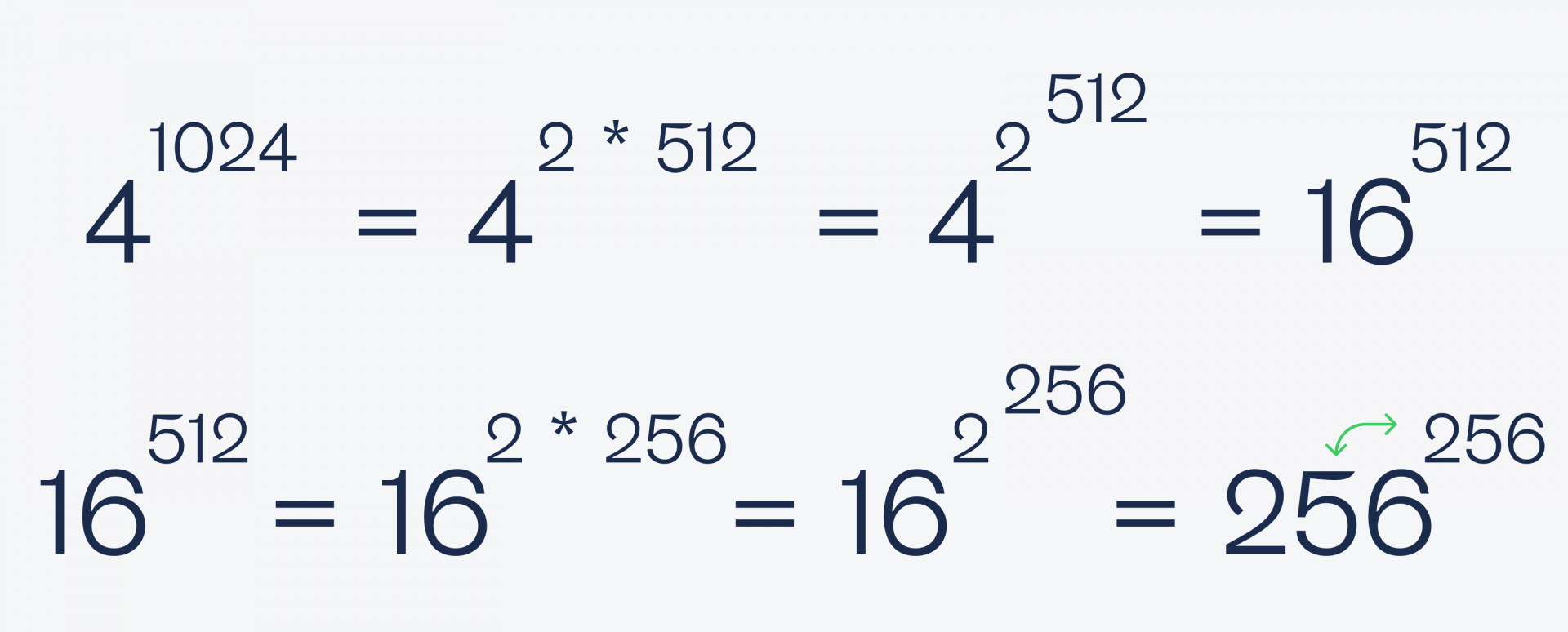
Получается, что X = 256. И не так сложно, как казалось в самом начале.
Очень сложная задача. Без калькулятора найти, чему это равно:
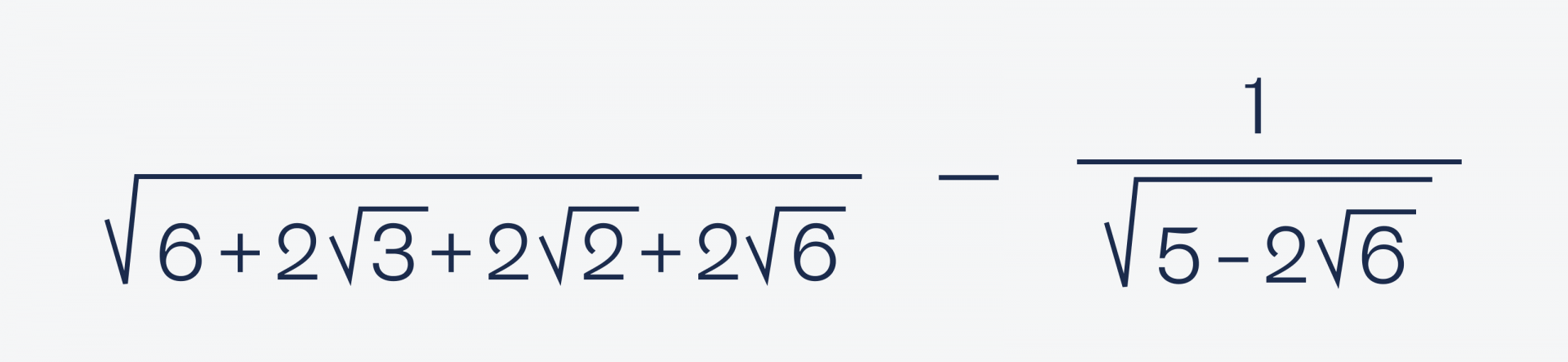
Это одна из тех задач, где в итоге всё получается просто и красиво. Сейчас убедимся в этом.
Сначала поработаем с левой частью: в ней есть √6. Чтобы его получить, нужно √2 умножить на √3.
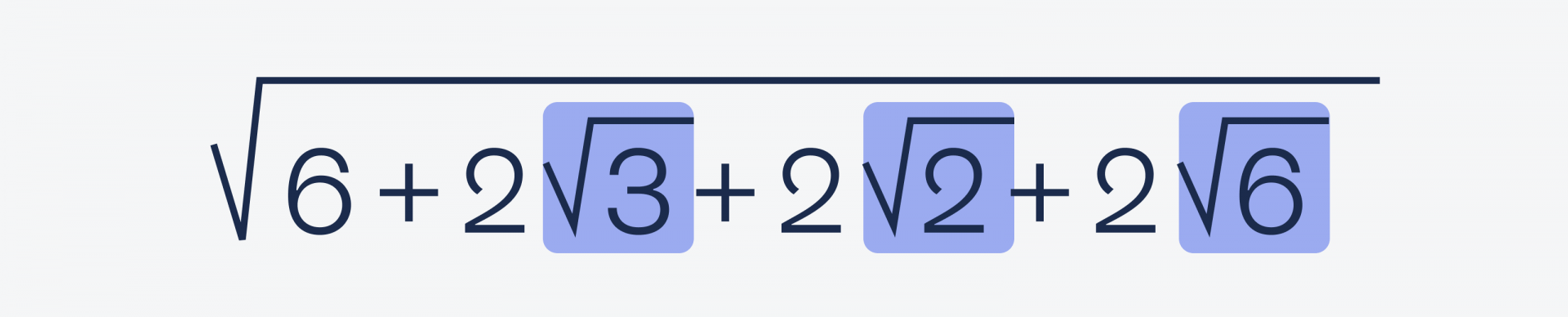
Но 2√6 — это удвоенное произведение, которое встречается в формуле квадрата суммы: (a + b)² = a² + 2ab + b².
Попробуем подставить сюда вместо a — √3 и вместо b — √2, чтобы получить удвоенное произведение, и посмотрим, что получится:
(√3 + √2)² = (√3)² + 2√2√3 + (√2)² = 3 + 2√6 + 2 = 5 + 2√6
Мы только что выяснили, что (√3 + √2)² = 5 + 2√6 — запомним это на будущее. А теперь посмотрим на левую часть под корнем ещё раз: в ней есть не 5 + 2√6, а 6 + √6, то есть на единицу больше:
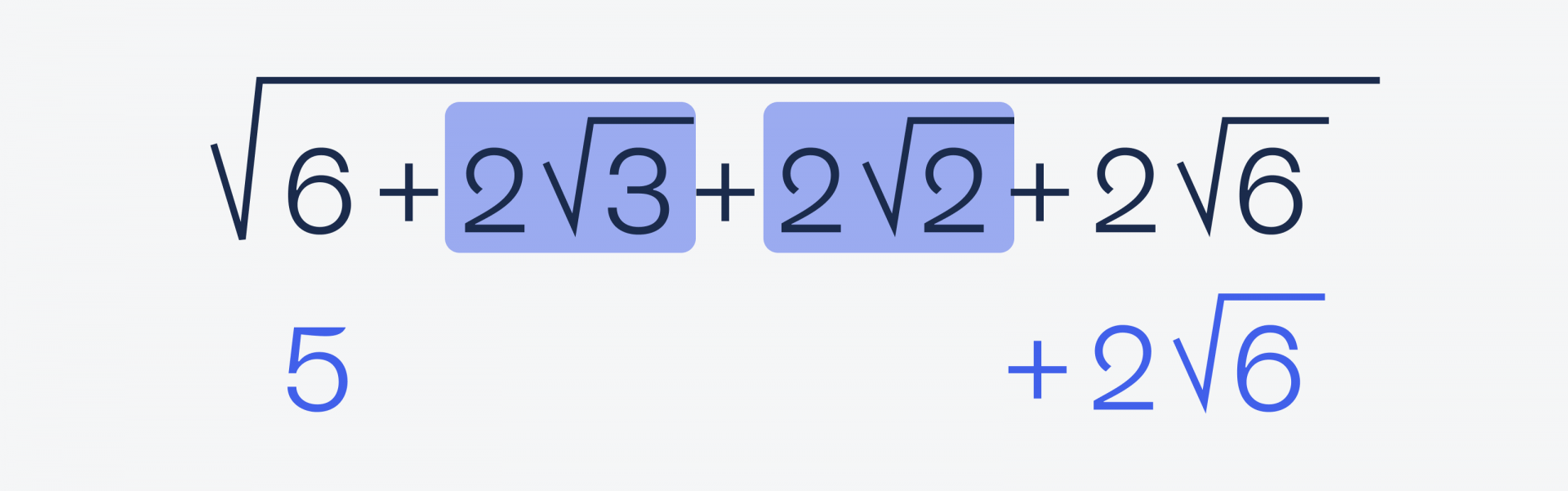
И там же есть удвоенные числа √2 и √3 — это значит, что мы можем проверить снова, вдруг из этого тоже можно сделать квадрат суммы.
Теперь самая сложная часть решения: раз 6 − 5 = 1, то пусть первым слагаемым будет единица, а вторым — (√3 + √2), чтобы мы получили 5 + 2√6 после возведения второго в квадрат. Проверим эту теорию:
(1 + (√3 + √2))² = 1² + 2(√3 + √2) + (√3 + √2)² = 1 + 2√3 + 2√2 + (√3 + √2)²
Но мы помним, что (√3 + √2)² = 5 + 2√6, поэтому вот что у нас получается:
1 + 2√3 + 2√2 + 5 + 2√6 = 6 + 2√3 + 2√2 + 2√6
Это именно то, что стоит у нас под корнем, значит, в левой части мы извлекаем корень из квадрата — а это будет равно как раз тому, что стоит в скобках:
√(1 + (√3 + √2))² = 1 + √3 + √2
Мы расправились с левой частью, теперь перейдём к правой:
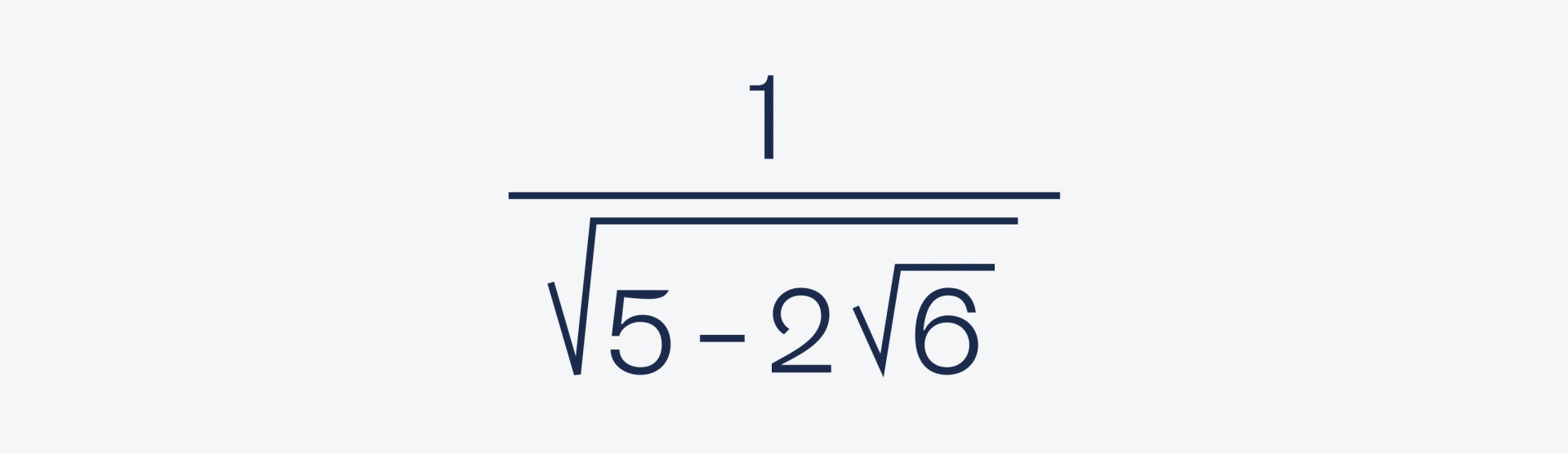
Чтобы избавиться от корня в знаменателе, умножим обе части на одно и то же число — √(5 + 2√6). Благодаря этому мы сможем возвести в квадрат оба слагаемых, потому что есть такое правило: (a + b) × (a − b) = a² − b².
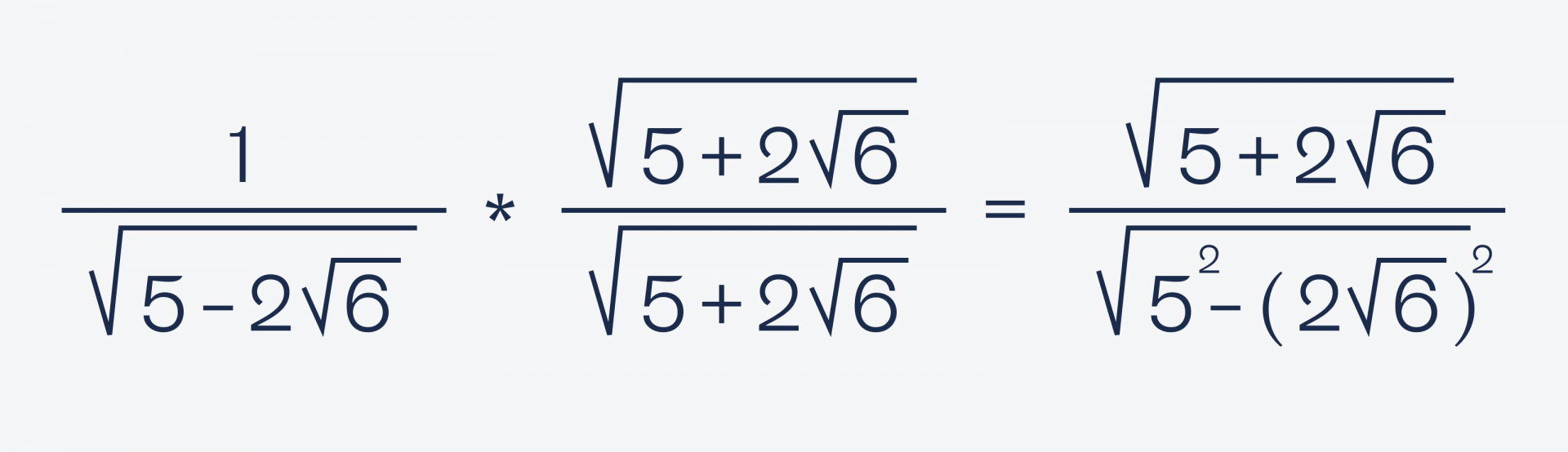
Посчитаем знаменатель:

Выходит, что вся наша дробь равна √(5 + 2√6). Но мы помним из первой части, что:
√(5 + 2√6) = (√3 + √2)²
Подставим это под знак корня:
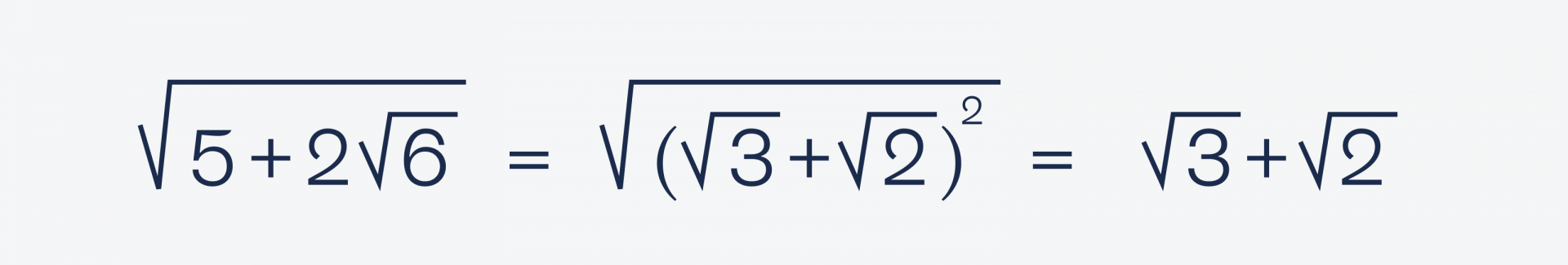
Значит, наша правая часть равна √3 + √2. Теперь отнимем это от левой части:
1 + √3 + √2 − (√3 + √2) = 1 + √3 − √3 + √2 − √2 = 1Получилась единица — простая и красивая, как мы и ожидали.