У нас накопилось так много задач про геометрию, что мы решили выпустить отдельную подборку с ними. Для решения нужны или простые формулы со школы, или смекалка (она у вас есть).
Погнали чертить.
Задачка от Джеффа Безоса. На размышление даётся 30 секунд
Перед вами очередная задачка с собеседований в крупные IT-компании. Вот сама задача:
Кабель длиной 80 метров висит на двух столбах. Высота каждого столба — 50 метров. Каково расстояние между столбами, если центр провисающего кабеля находится:
а) на высоте 20 метров от земли — вариант для технарей;
б) на высоте 10 метров от земли — вариант для гуманитариев.
Для решения можно использовать инженерный калькулятор с расширенными функциями.
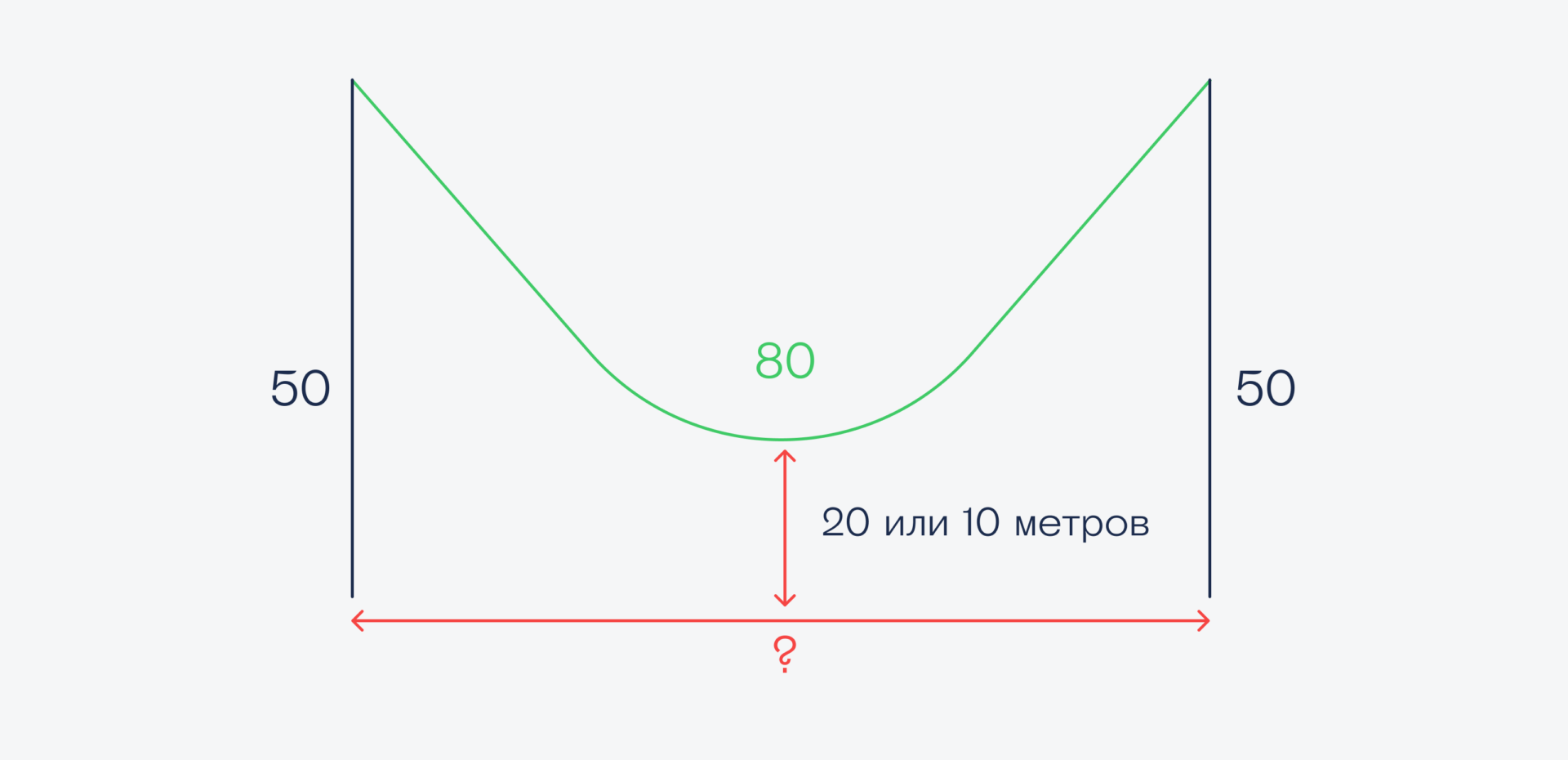
В задаче нет никакого подвоха, но для решения нужно хорошо знать математику, углы и угловые функции. Попробуйте сначала решить её самостоятельно, а потом загляните в решения.
Первое, что мы сделаем, — поднимем уровень земли, чтобы он касался провода. Так как до центра провиса 20 метров, то высота столбов тоже уменьшится на эти 20 метров:
Расстояние между столбами у нас при этом осталось тем же самым.
Так как кабель провисает по центру, нам достаточно найти расстояние от края до середины и умножить его на 2 — так мы найдём полное расстояние между столбами.
❗️ Самая важная часть.
Так как провисающий кабель похож на гиперболу, то мы для решения будем использовать не тригонометрические функции, которые работают с прямыми и окружностями, а гиперболические, график которых похож на гиперболу.
Если нужно точное описание этих функций — вот оно:
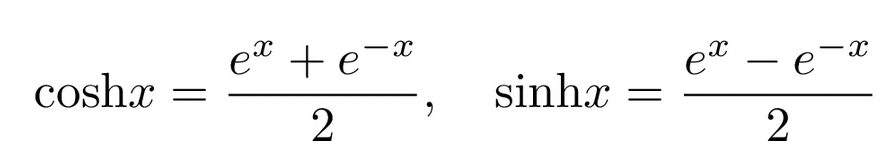
Сначала поработаем с высотой столба. Запишем формулу для расстояния, затем добавим на рисунок те данные, которые мы уже знаем, и раскроем формулу:
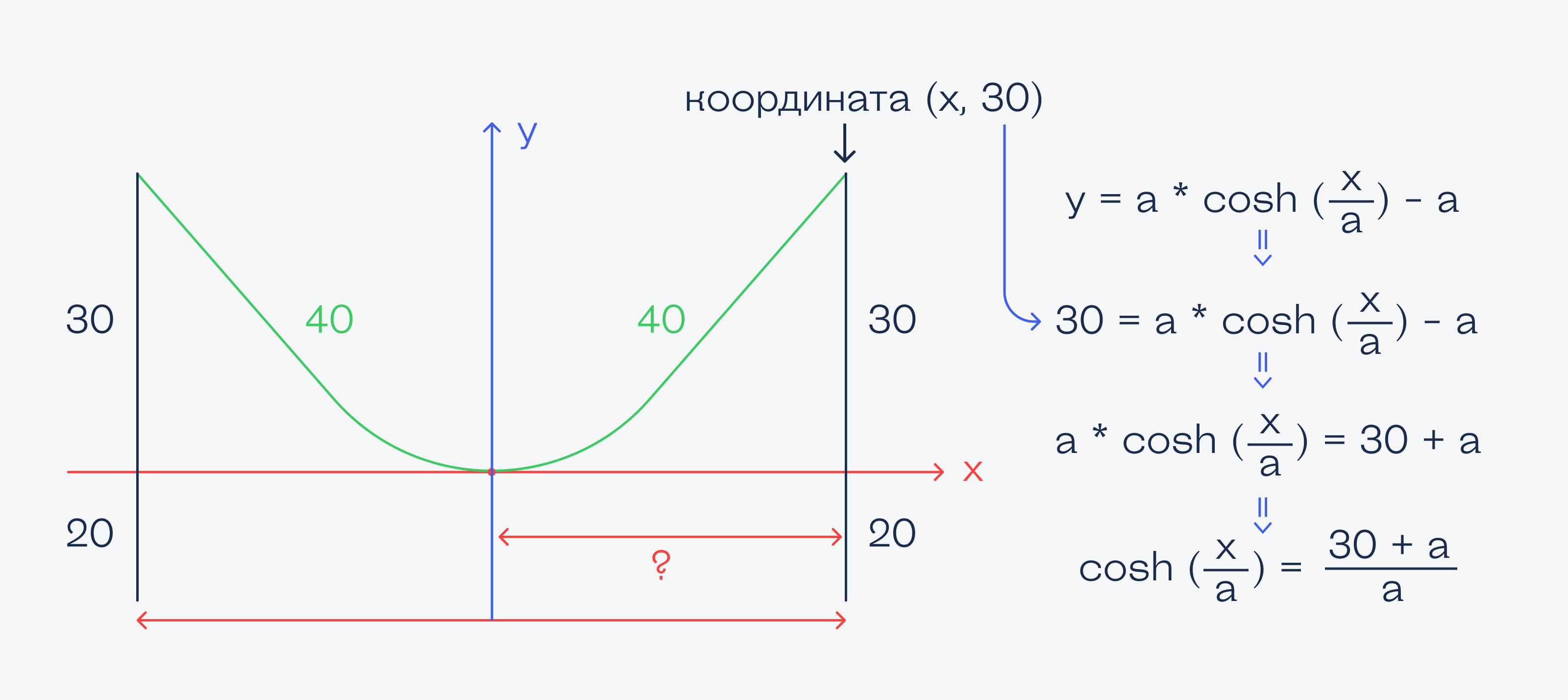
Теперь составим второе уравнение, в котором используем значение длины кабеля. Так как он провисает ровно посередине, то его длина от края до точки перегиба — 40 метров.
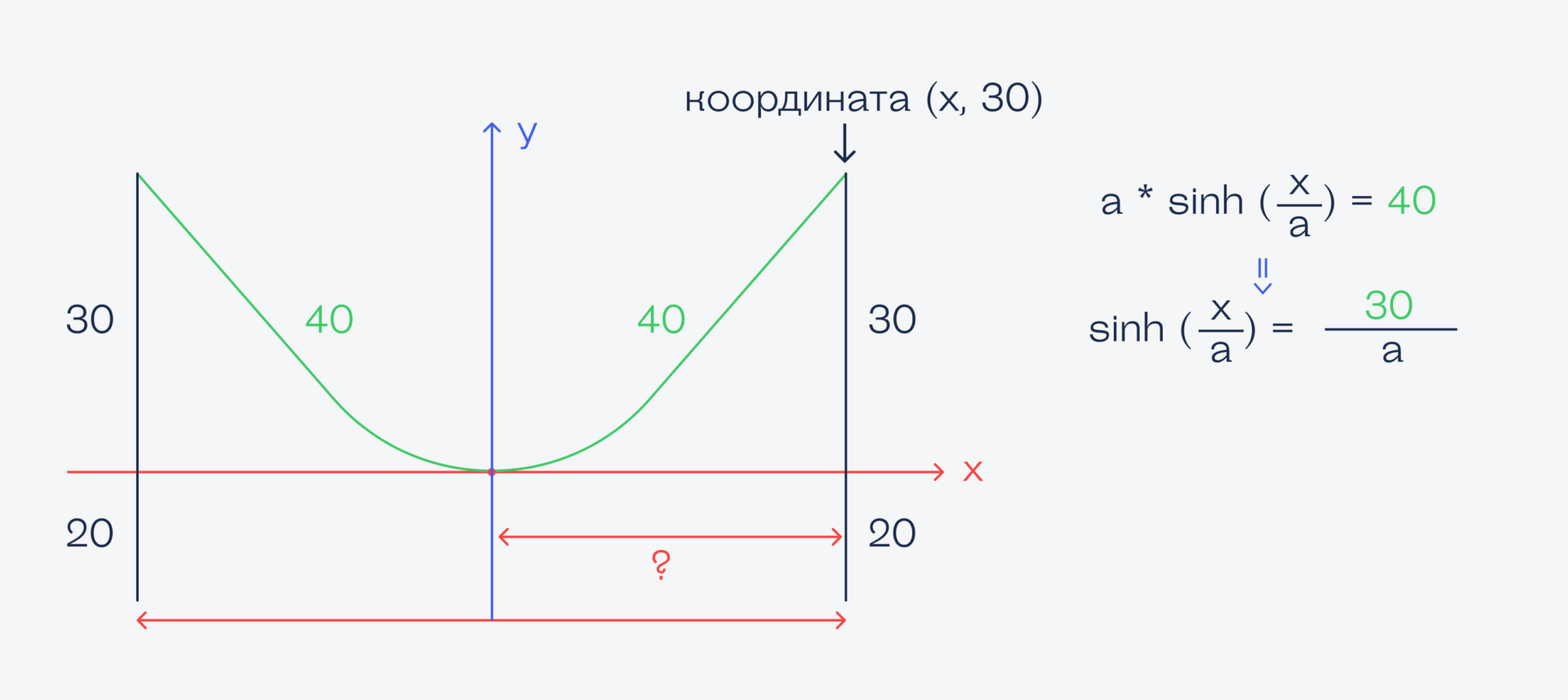
Добавляем свойство о том, что разность квадратов гиперболического синуса и косинуса равна единице:
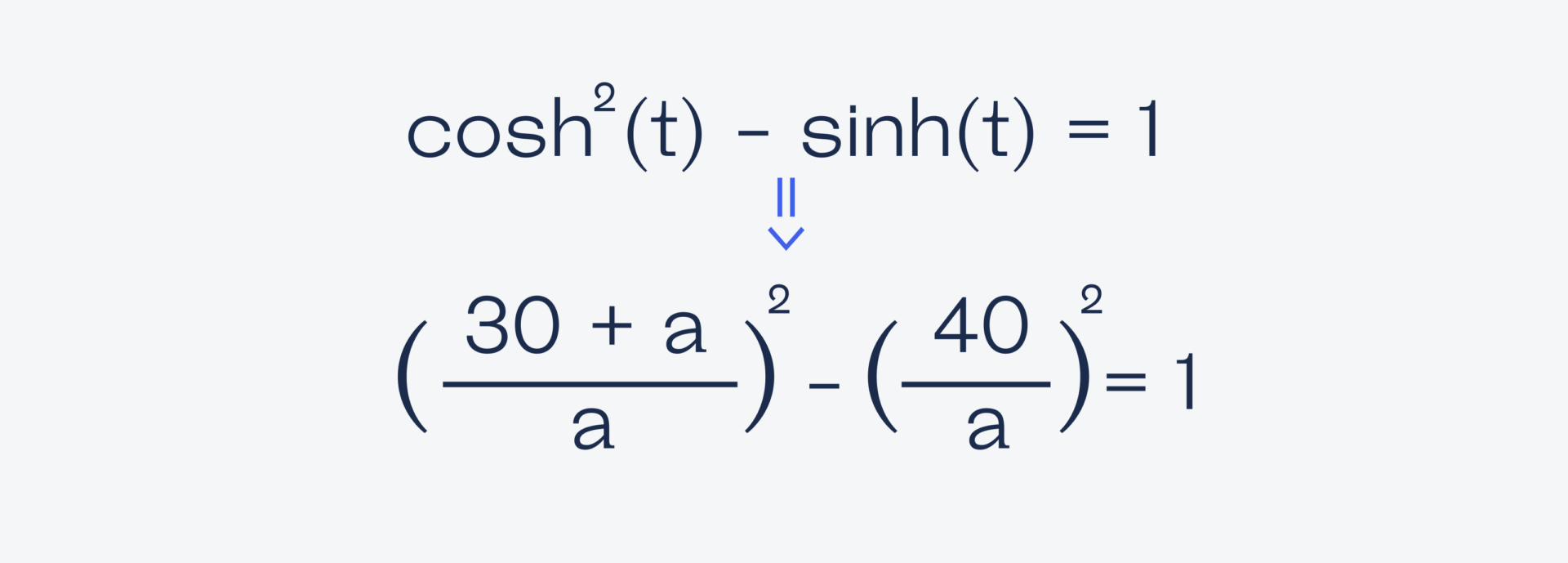
Раскрываем скобки, приводим всё к классическому квадратному уравнению и, решая его, получаем ответ: a = 35/3.
Это значение подставляем в формулу гиперболического синуса, чтобы посчитать половину длины кабеля:
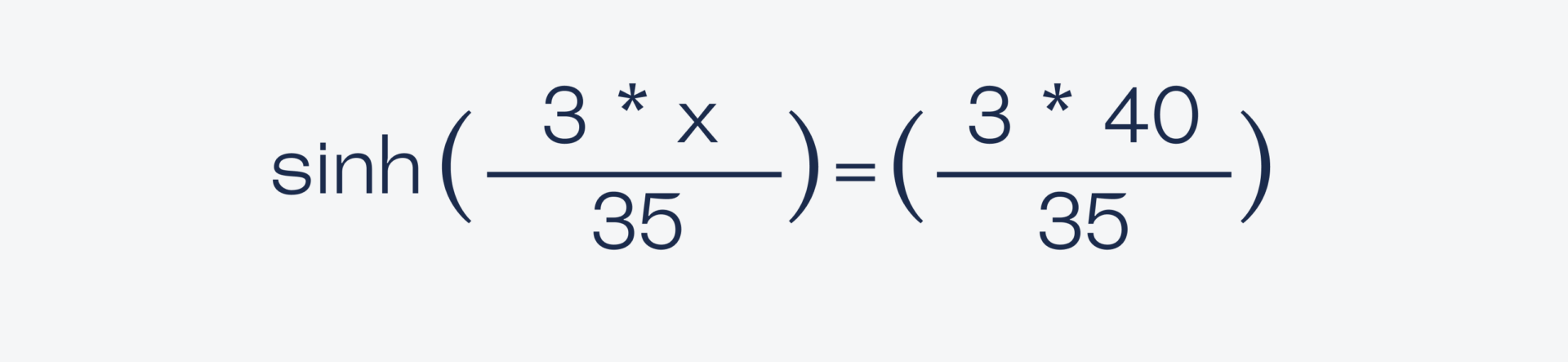
Решаем это уравнение на калькуляторе и получаем ответ: x ≈ 22,7. Это половина расстояния между столбами, а полное расстояние ≈ 45,4 метра.
Ответ: если высота до центра провиса равна 20 метров, то расстояние между столбами составляет примерно 45,4 метра.
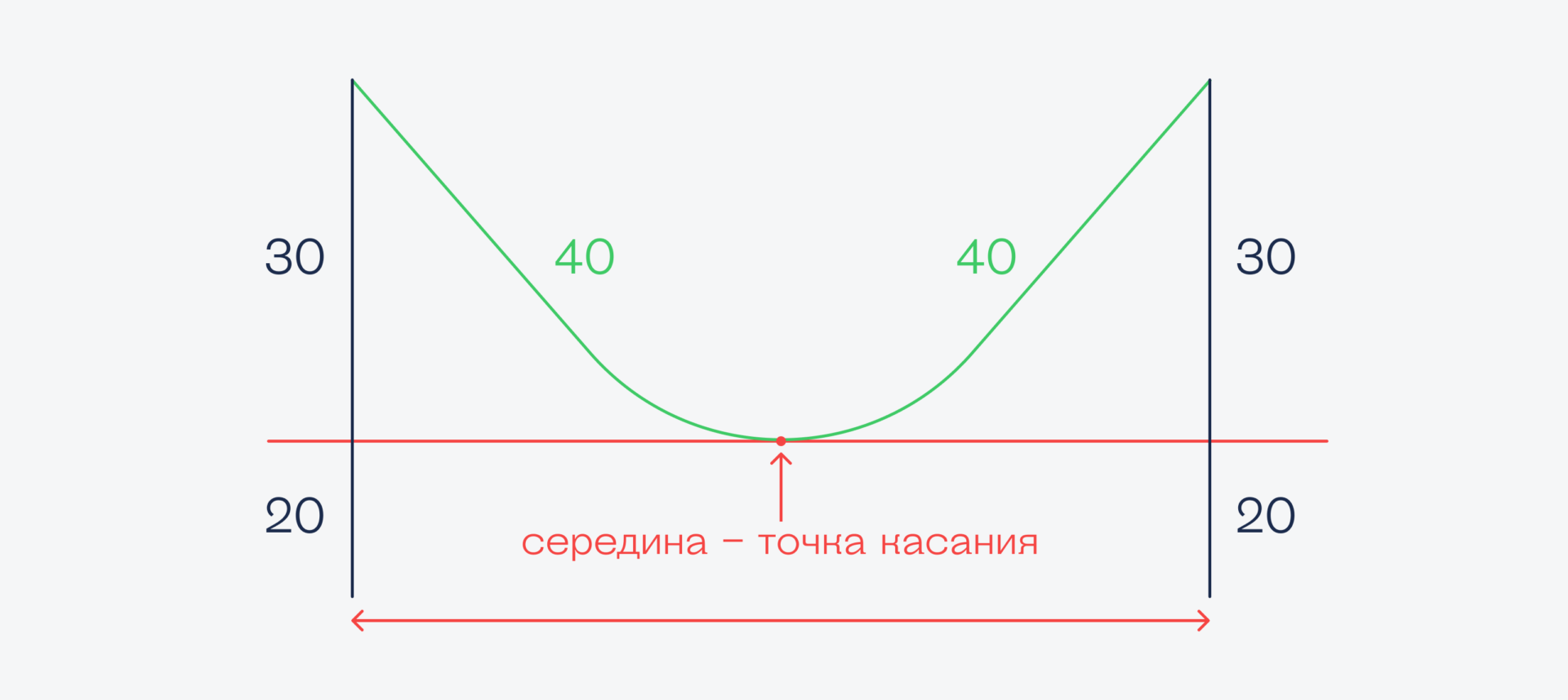
У гуманитариев кабель длиной 80 метров провисает на минимальной высоте 10 метров от земли. При этом высота столба 50 метров. Значит, если провести новый «уровень земли» (красным), верхняя часть столба будет равняться 40 метрам.
Посмотрите на рисунок. Нет ли здесь ошибки?
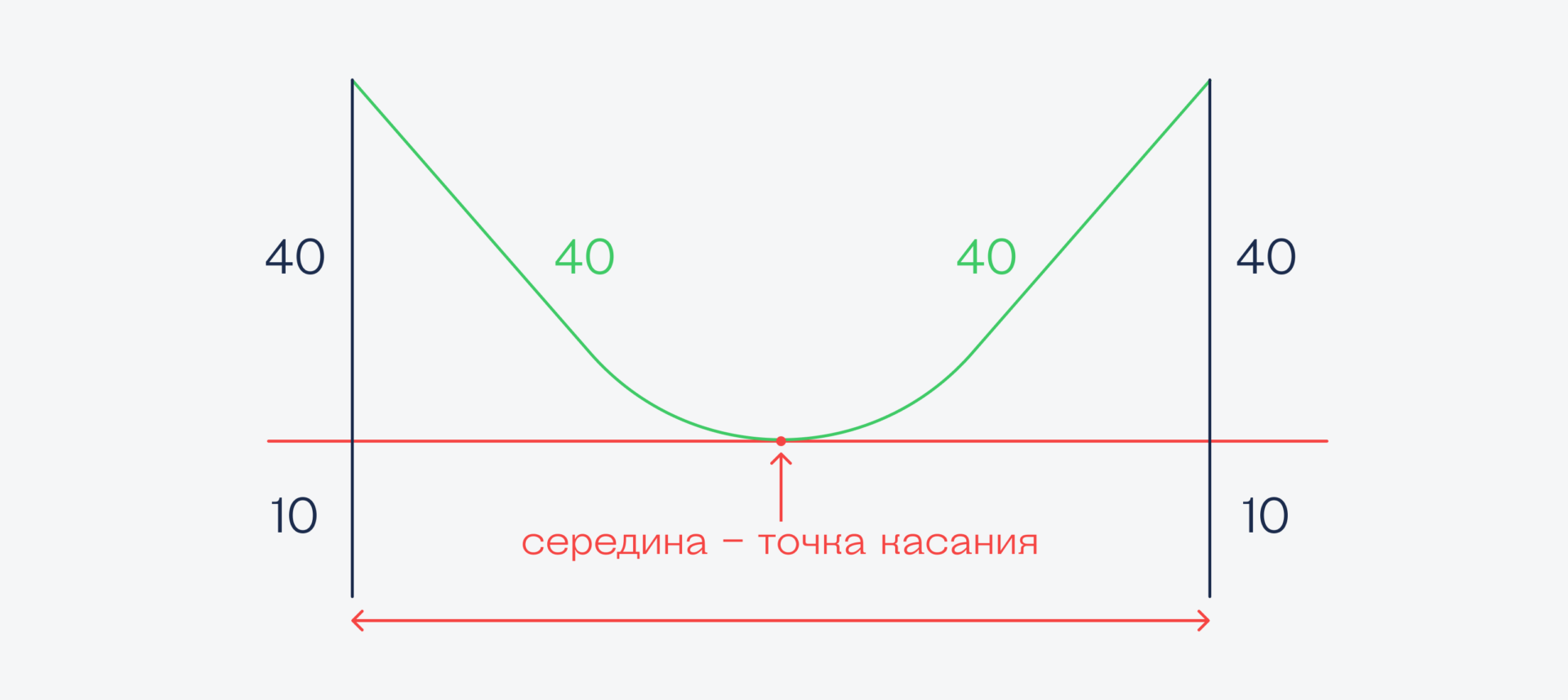
Если верхняя часть столба 40 метров и длина кабеля до середины — тоже 40 метров, то какой это треугольник? Может ли такой треугольник существовать?

Простая задача про круги, которая выглядит сложной
Дано: есть три одинаковых круга с диаметром в 1 метр. Круги соприкасаются друг с другом, а вокруг них натянута эластичная лента.
Что нужно: найти длину этой ленты.
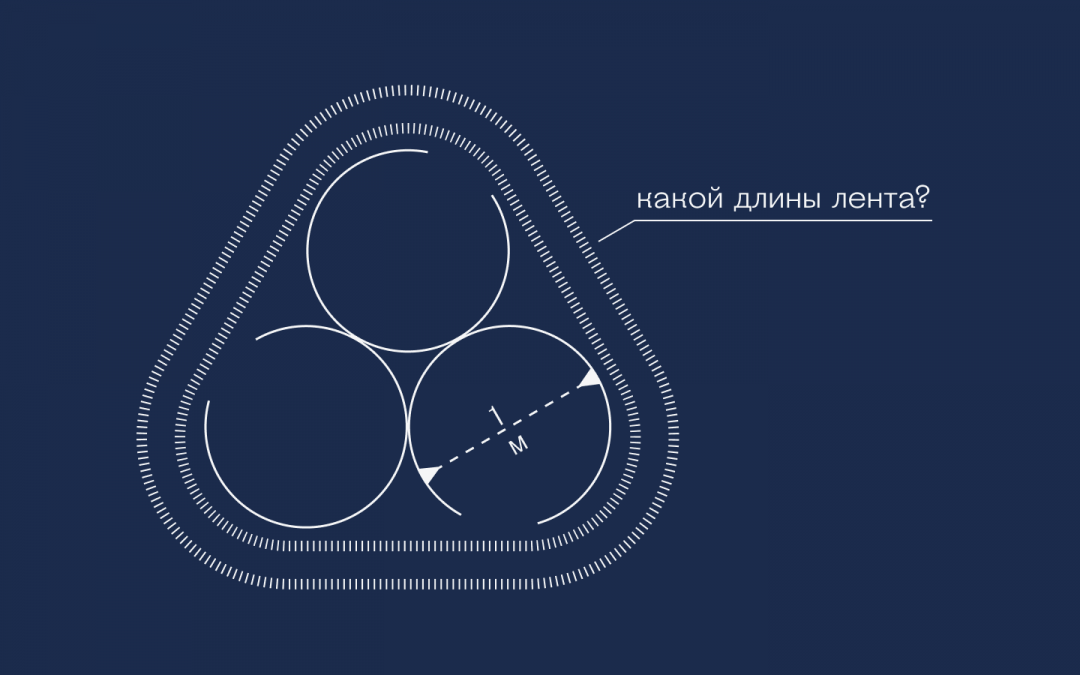
Кажется, что это очень сложная задача, где нужно знать сложные формулы расчёта кривизны и точек натяжения, но на деле всё будет гораздо проще. Если знаете английский — посмотрите оригинальный ролик, там классная анимация:
Строим внутренний треугольник
Первое, что мы сделаем, — соединим центры всех кругов в один треугольник:

В геометрии есть такое правило, что если круги касаются друг друга, то через их центры можно провести прямую линию, и точка касания кругов будет лежать на этой линии. Раз у нас диаметр равен 1, то радиус каждого круга равен 0,5. Обозначим это на рисунке:

Получается, что длина каждой стороны треугольника равна 0,5 + 0,5 = 1. Запомним это и идём дальше.
Строим проекцию
От каждой вершины треугольника проведём под прямым углом линии к ленте:
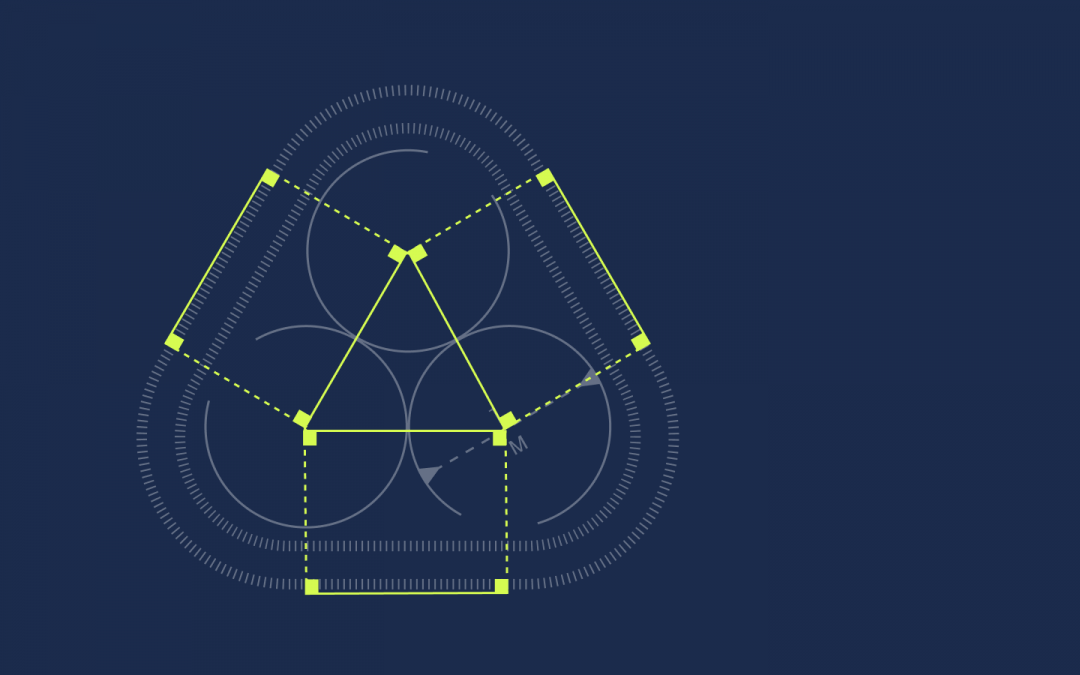
Получились прямоугольники. У прямоугольников противоположные стороны равны, поэтому раз стороны треугольника равны единице, то и эти отрезки на ленте тоже будут равны единице:
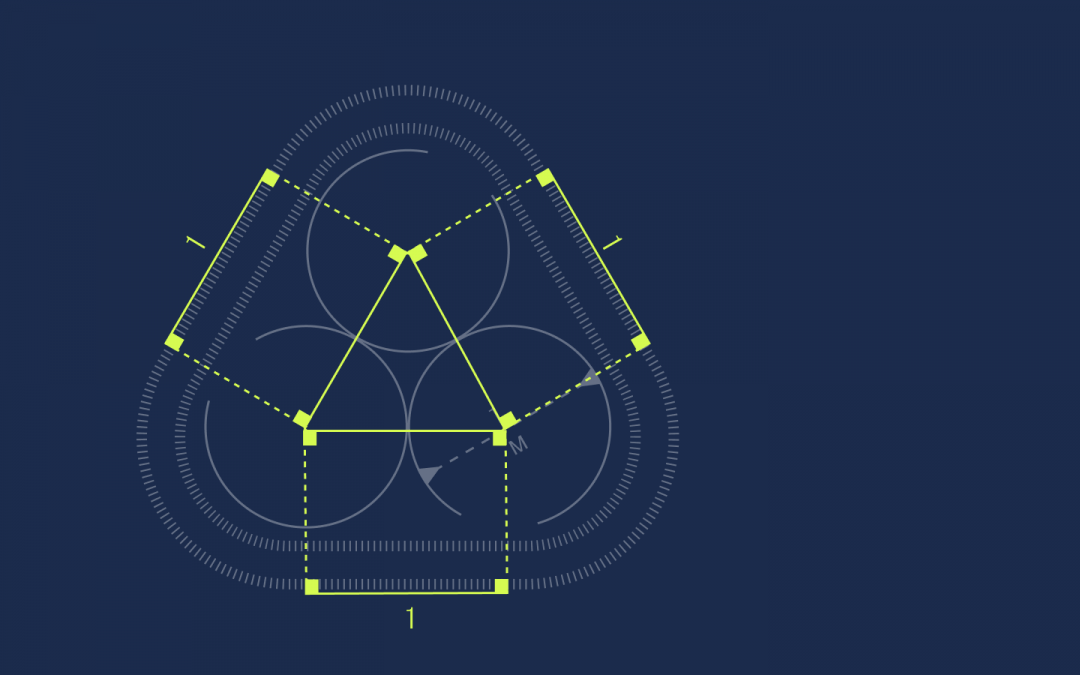
Осталось найти длину оставшихся секций:
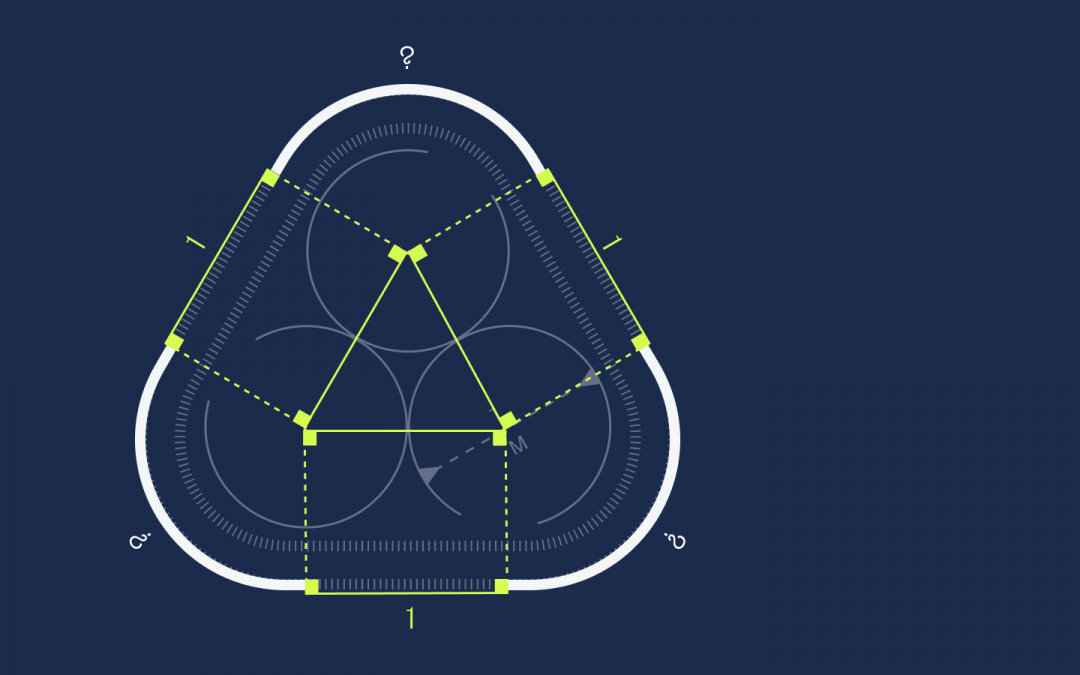
Вычисляем длину секций
Здесь нам поможет знание о том, что полный оборот внутри круга — это 360 градусов.
Так как во внутреннем треугольнике все стороны равны, то это равносторонний треугольник. А раз так, то углы в нём равны 60 градусов. Добавим сюда по два прямых угла по 90 градусов из прямоугольников:
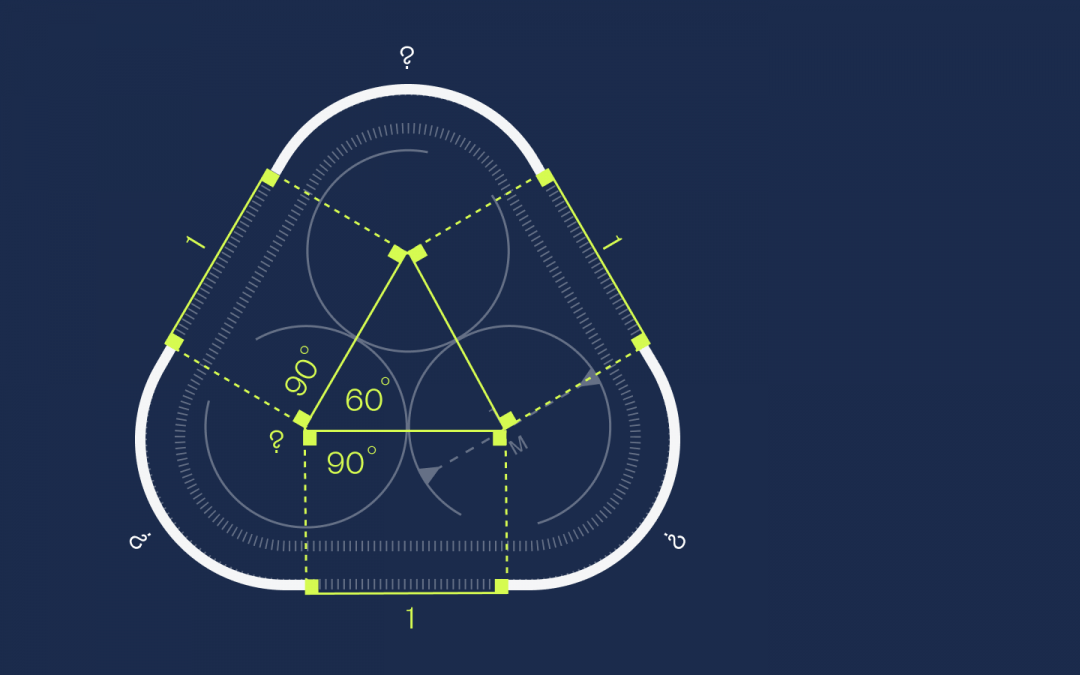
Решаем уравнение: 90 + 60 + 90 + X = 360 → X = 120 градусов.
Но 120 градусов — это ровно треть круга, а у нас таких частей как раз три:
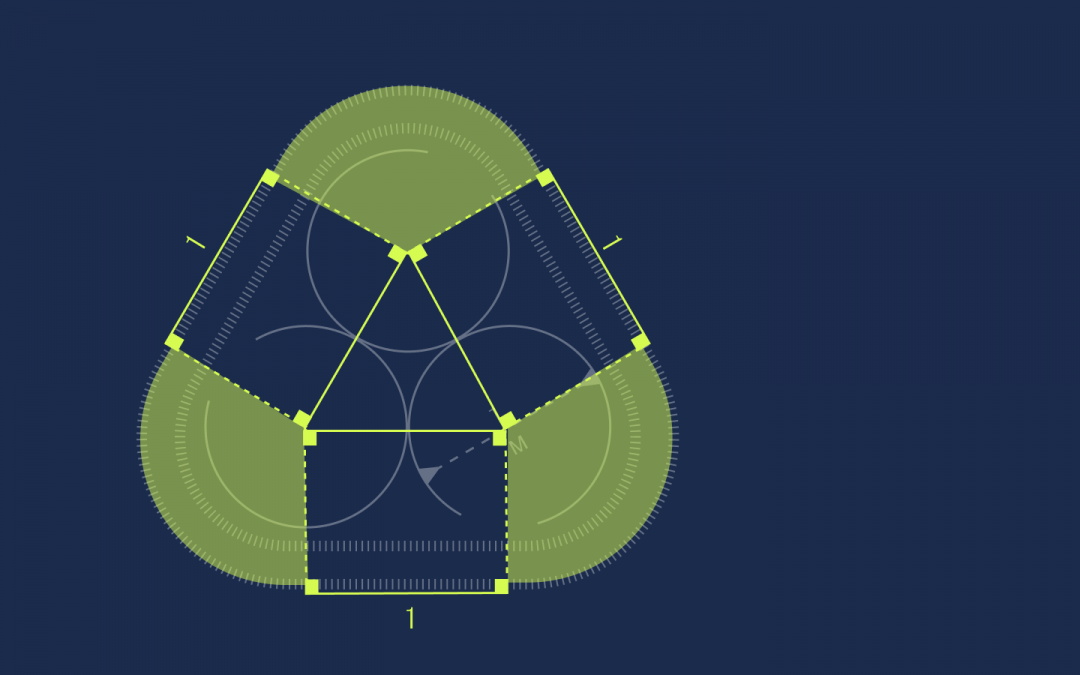
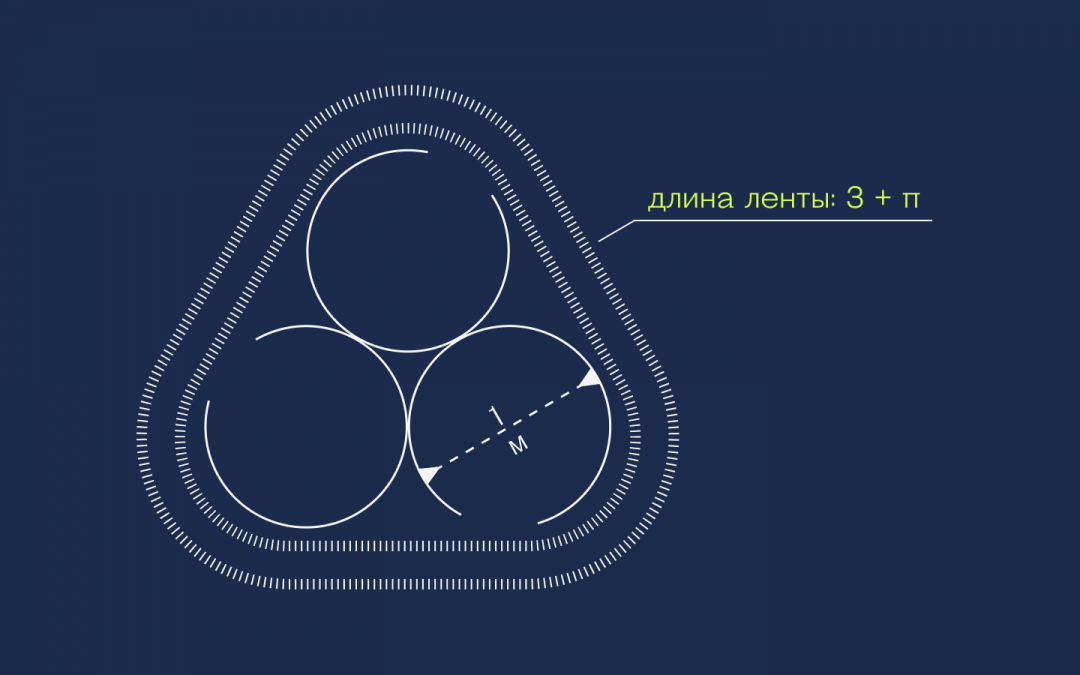
Это значит, что из них можно составить один целый круг. При этом мы знаем, что у этого круга радиус 0,5, а диаметр тогда равен единице. Этого достаточно, чтобы посчитать длину окружности: L = π × d → L = 3,14.
Складываем это число с длинами трёх отрезков и получаем полную длину: 3 + π
Как найти площадь прямоугольника?
Старая задачка для тех, кто устал от сложных расчётов: найдите площадь маленького прямоугольника внутри большого прямоугольника (он выделен синим):
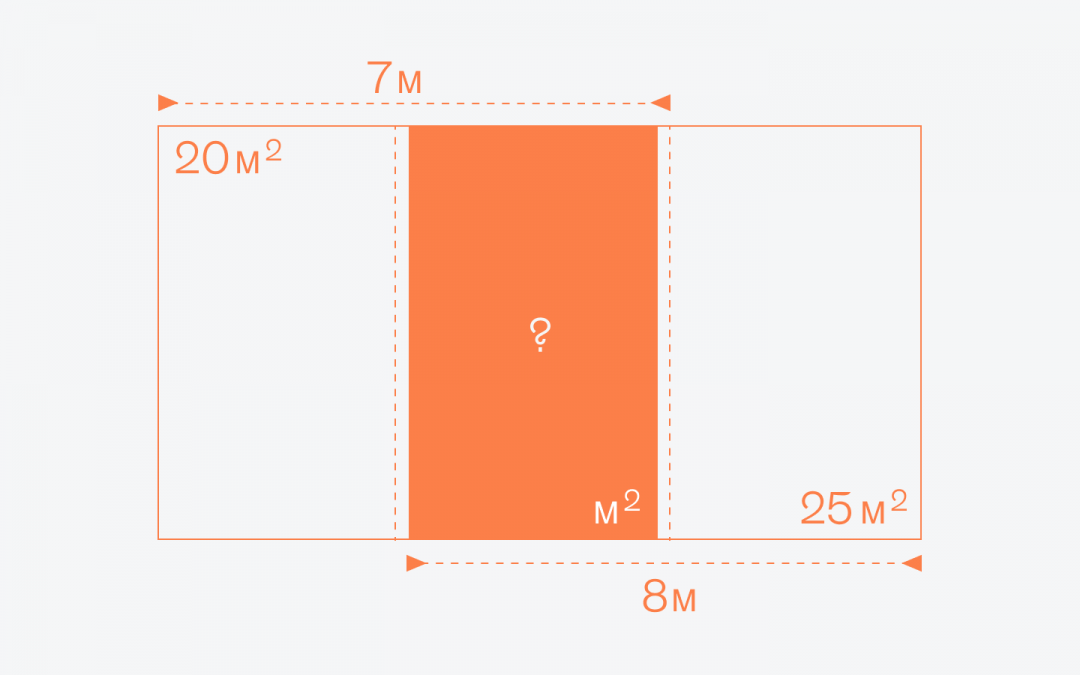
Чтобы решить эту задачу, обозначим ширину синего прямоугольника за X. Заодно уберём метры и квадратные метры, чтобы не мешали:
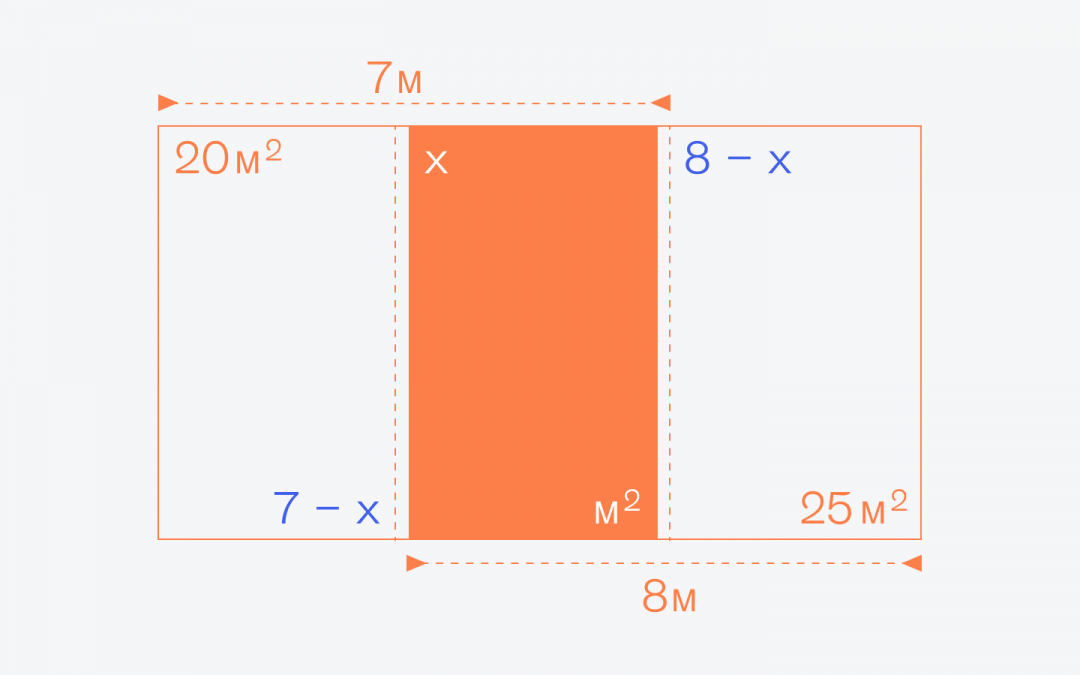
Отлично, у нас появилась ширина у тех прямоугольников, у которых известна площадь. Осталось добавить высоту Y — так как большая фигура тоже прямоугольник, то высота всех внутренних прямоугольников также будет одинаковой:
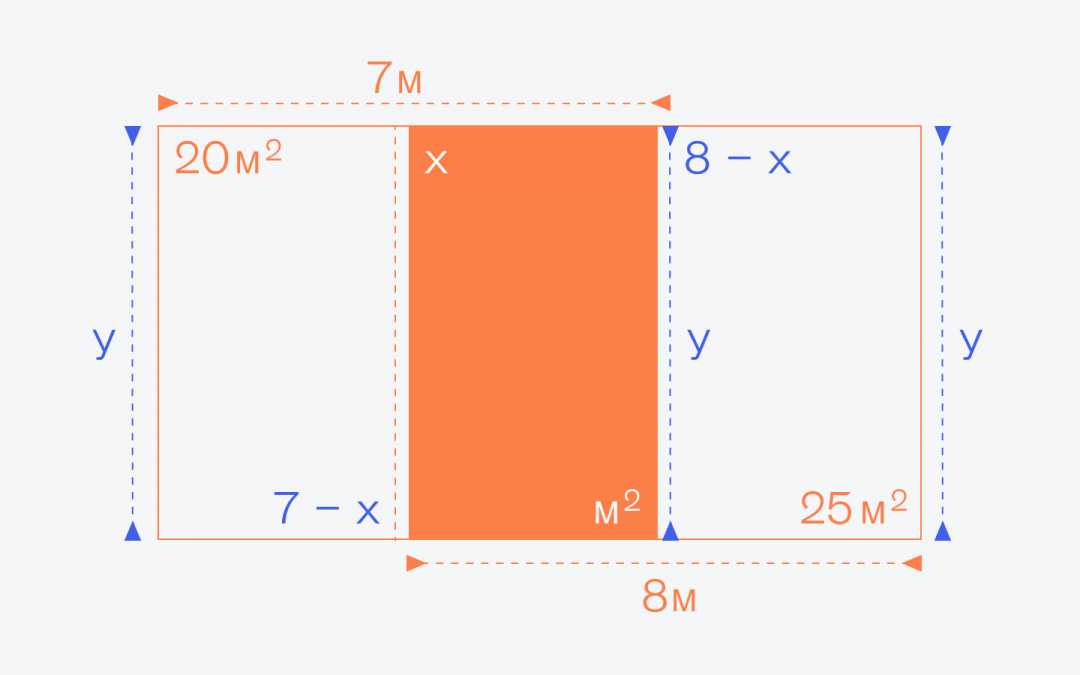
Теперь, когда у нас есть размеры и площади прямоугольников, мы можем составить два равенства:
(7 − x) × Y = 20
(8 − X) × Y = 25
Получилось два уравнения с двумя неизвестными, а значит, их можно объединить в систему и решить:
7Y − XY = 20
8Y − XY = 25
Вычтем первое уравнение из второго:
(8Y − 7Y) − (XY − XY) = 25 − 20
Y = 25 − 20 = 5.
Теперь подставим это значение в первое уравнение:
7 × 5 − 5X = 20
35 − 5X = 20 → 5X = 35 − 20 → 5X = 15 → X = 3.
В самом начале мы обозначили ширину синего прямоугольника за X, а потом высоту — за Y. Значит, его площадь будет равна X × Y. А раз мы уже знаем оба эти значения, то получается, что площадь синего треугольника равна 3 × 5 = 15 квадратных метров.
Задача про периметр и забывчивого монтажника
Одному монтажнику поставили задачу — подготовить кабель для камер видеонаблюдения на первом этаже здания. Само здание прямоугольное, а стены между комнатами делят этаж на 4 комнаты-прямоугольника. В техническом условии было написано, что кабель в каждой комнате должен идти точно по периметру стен, поэтому монтажник измерил периметр каждой комнаты и записал всё на листочке. Но он спешил, поэтому в магазине обнаружил, что забыл записать периметр последней комнаты:

Помогите монтажнику найти периметр последнего прямоугольника, чтобы ему не пришлось лишний раз возвращаться на объект.
Обозначим буквами стороны каждого прямоугольника:
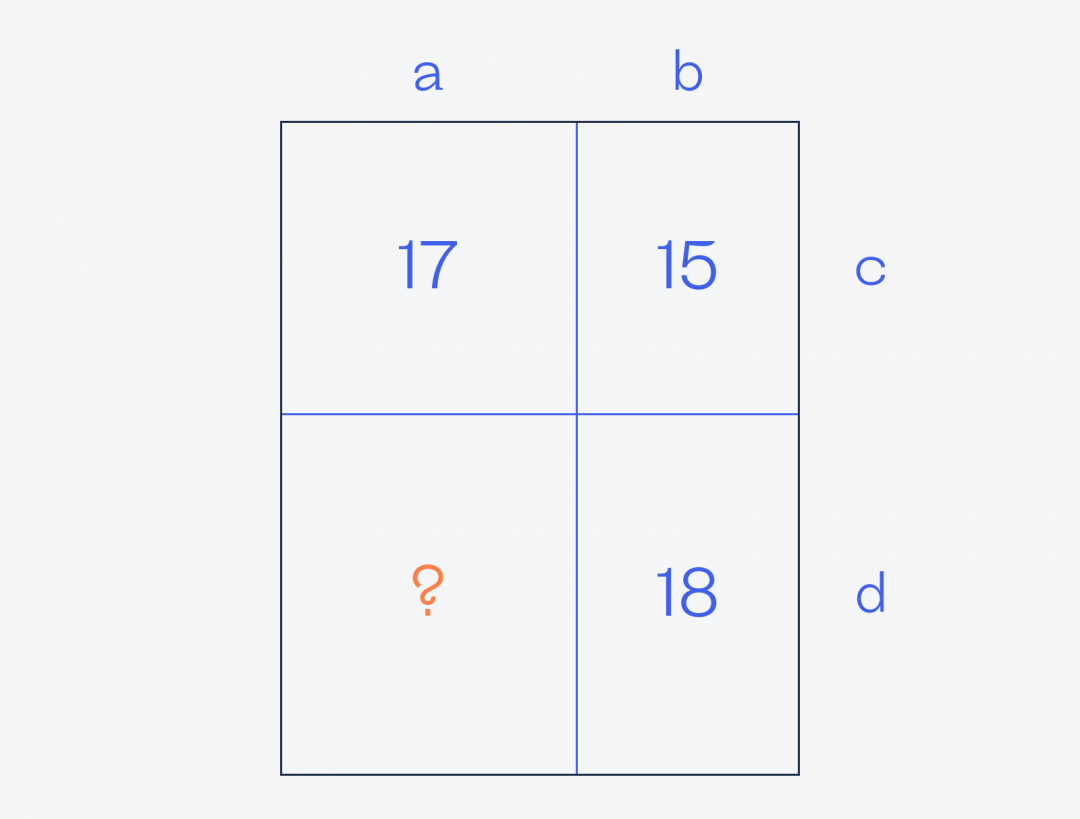
Теперь, когда у нас есть обозначения сторон, запишем то, что нам уже известно:
2а + 2с = 17
2b + 2c = 15
2b + 2d = 18
Периметр последнего прямоугольника равен 2a + 2d — эту сумму мы и будем искать в решении.
Возьмём первое уравнение и посчитаем, чему равно 2c, чтобы подставить это во второе уравнение:
2c = 17 − 2a → подставляем во второе уравнение
2b + 17 − 2a = 15 → 2b − 2a = 15 − 17 → 2b − 2a = −2
Теперь отсюда выясним, чему равно 2b, и подставим это в третье уравнение:
2b − 2a = −2 → 2b = 2a − 2 → подставляем в третье уравнение:
2a − 2 + 2d = 18
2a = 2d = 18 + 2
2a + 2d = 20
Но периметр последней комнаты как раз равен 2a + 2d, а значит, он равен 20.
Мэтимэтикс.
Задача про три участка и роутер
Для решения этой задачи потребуется вспомнить тригонометрию. Вспомним же её!
Три брата купили квадратные участки в лесном посёлке. Участки одинакового размера. Длина каждого участка — 100 метров, а расположены они треугольником:
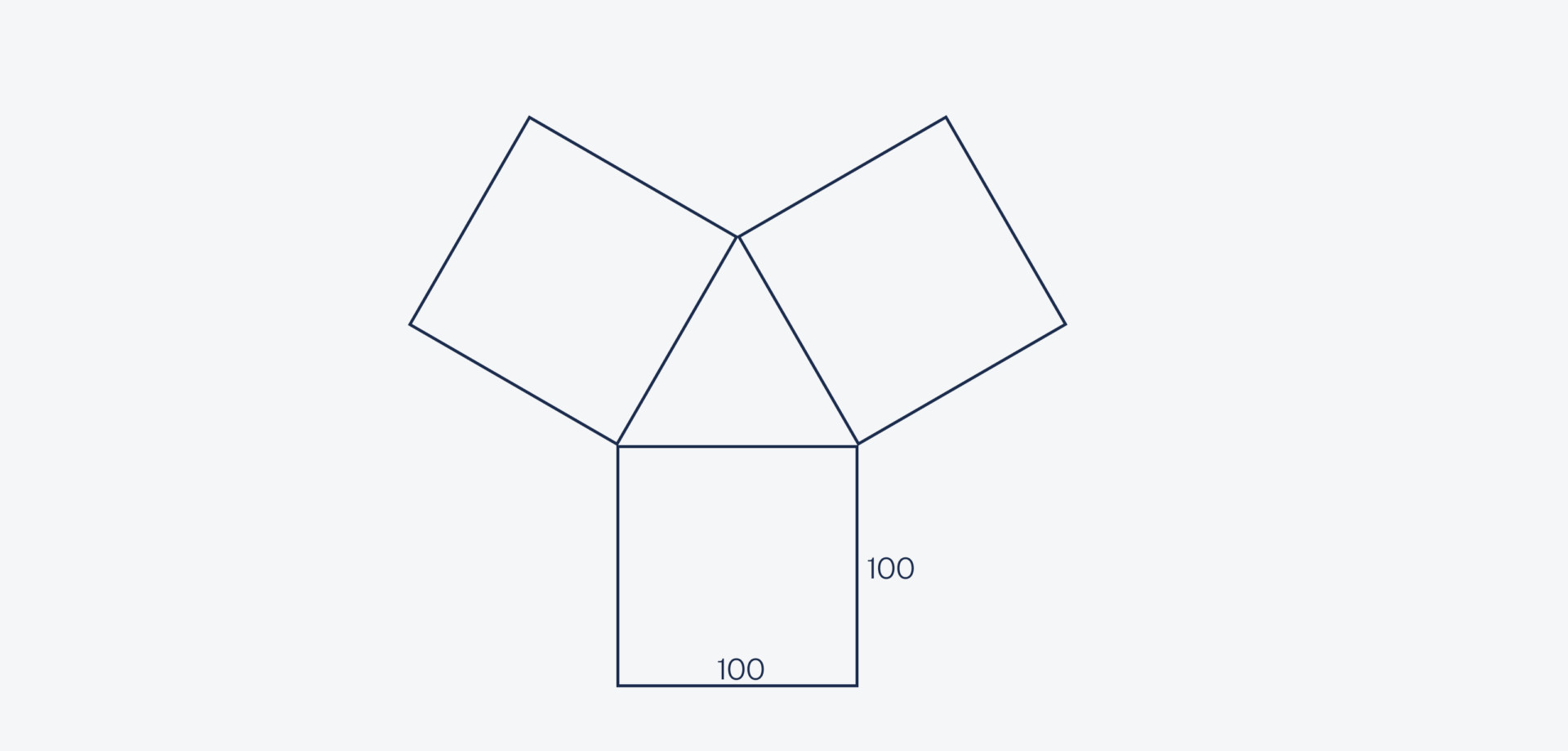
Братья решили сэкономить на интернете и поставить один роутер на троих. Чтобы найти точку, одинаково близкую ко всем участкам, они вплотную обвели три квадрата в круг и поставили роутер точно в центре получившегося круга.
Но братья не учли, что сигнал роутера дотягивается только на 130 метров, а дальше интернет теряется. Хватит ли братьям этого роутера или нужно взять мощнее?
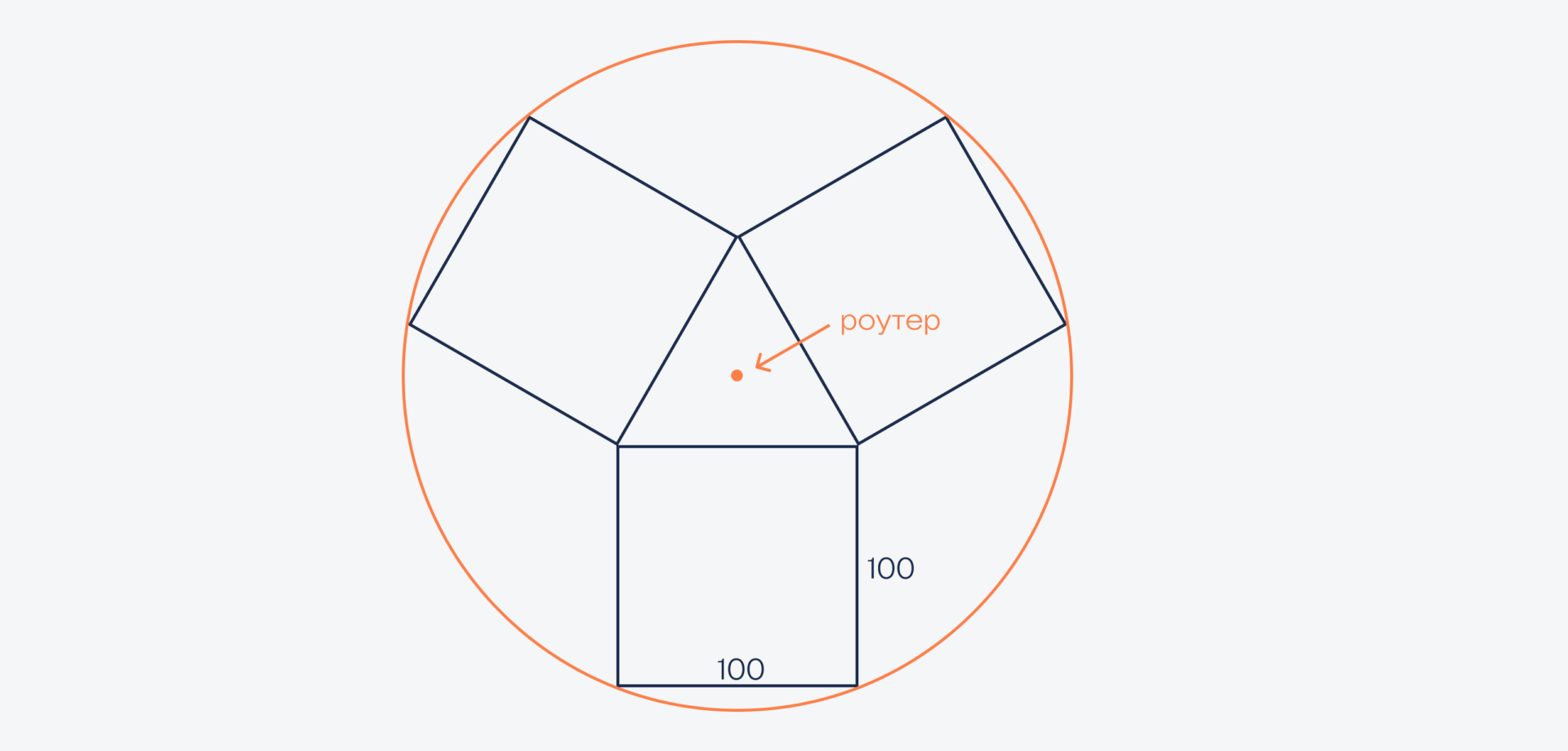
Чтобы понять, хватит ли братьям этого роутера, нужно выяснить, какого радиуса круг у них получился. Если радиус будет меньше, чем радиус покрытия роутера, то всё в порядке, а если нет — роутер придётся менять.
Первым делом проведём через круг три диаметра, каждый из которых будет проходить через вершину треугольника. Длина каждой стороны треугольника — тоже 100 метров, так как он образован сторонами квадрата:
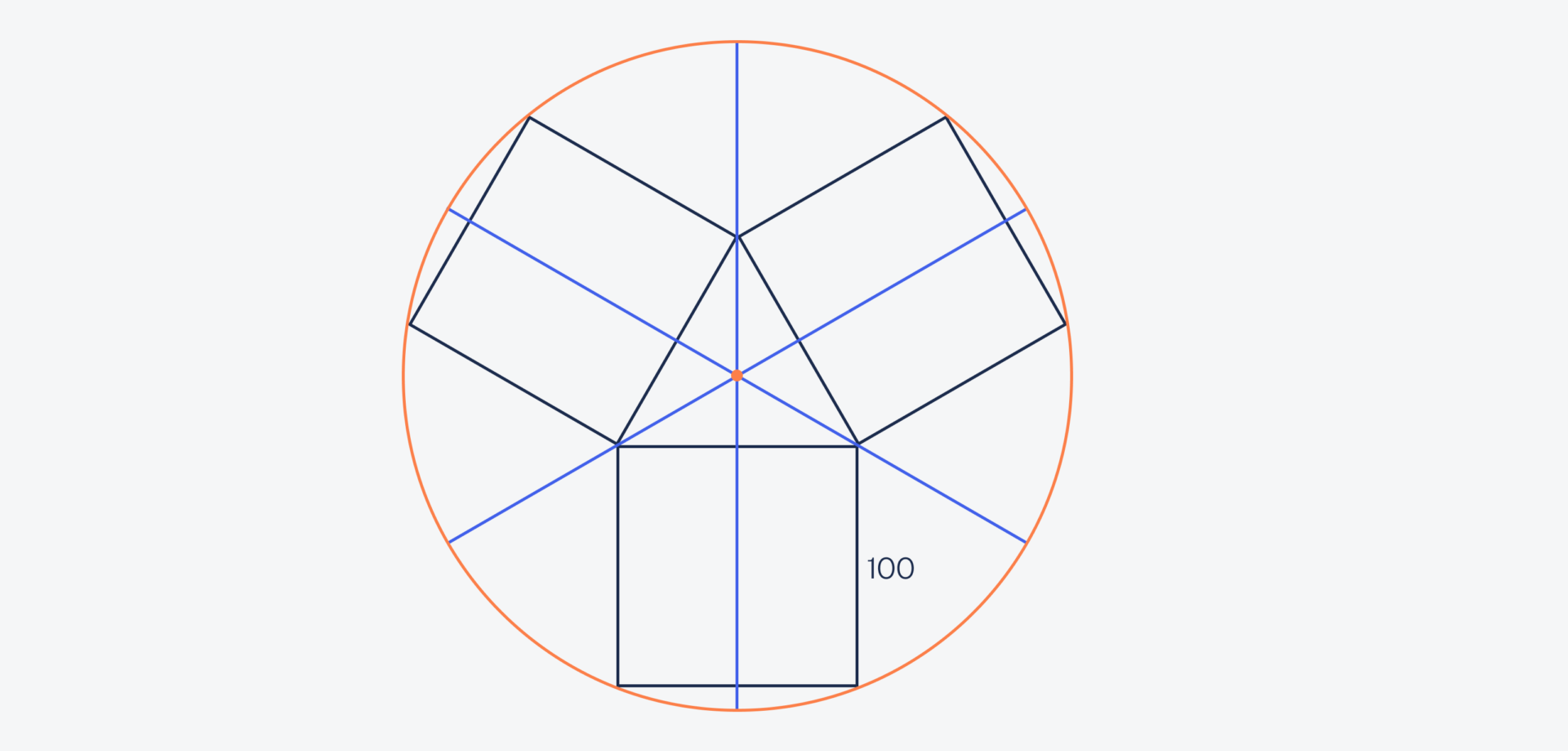
Раз все три линии в равностороннем треугольнике пересекаются в одной точке, то каждая линия — одновременно биссектриса (делит угол пополам) и медиана (делит противоположную сторону пополам), а ещё она проходит под прямым углом к противоположной стороне. А раз участки квадратные, то и противоположную сторону эта линия тоже пересекает под прямым углом и тоже делит ту сторону пополам:
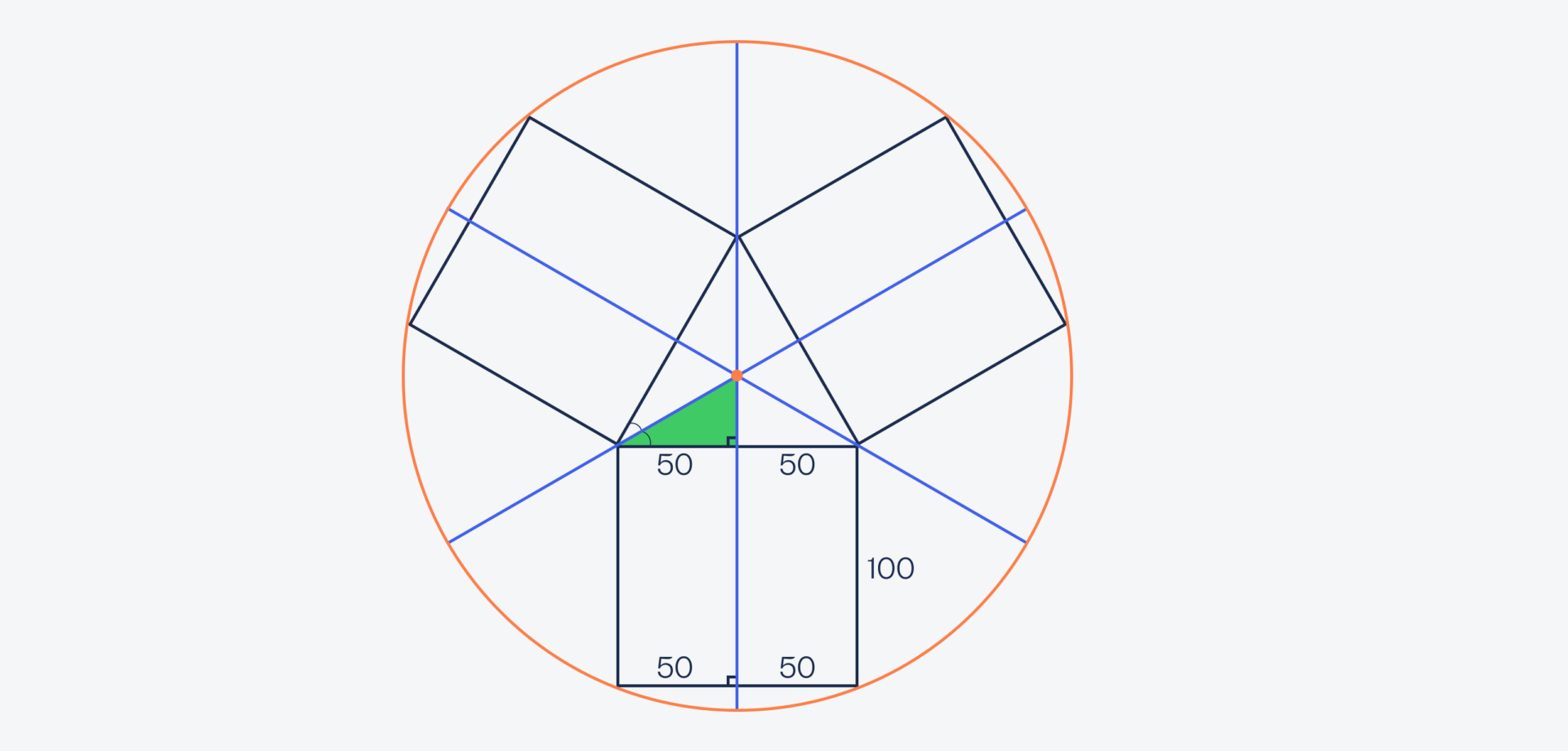
Теперь посмотрим поближе на центральный треугольник, а точнее — на один из маленьких треугольников, который получился в результате. Так как каждая синяя линия — это биссектриса, а в равностороннем треугольнике все углы по 60 градусов, то левый угол будет равен 30 градусам. Мы знаем, что сумма всех углов треугольника равна 180 градусов, и у нас уже есть два угла — 30 и 90 градусов. Это значит, что верхний угол будет равен 180 − 90 − 30 = 60 градусов:
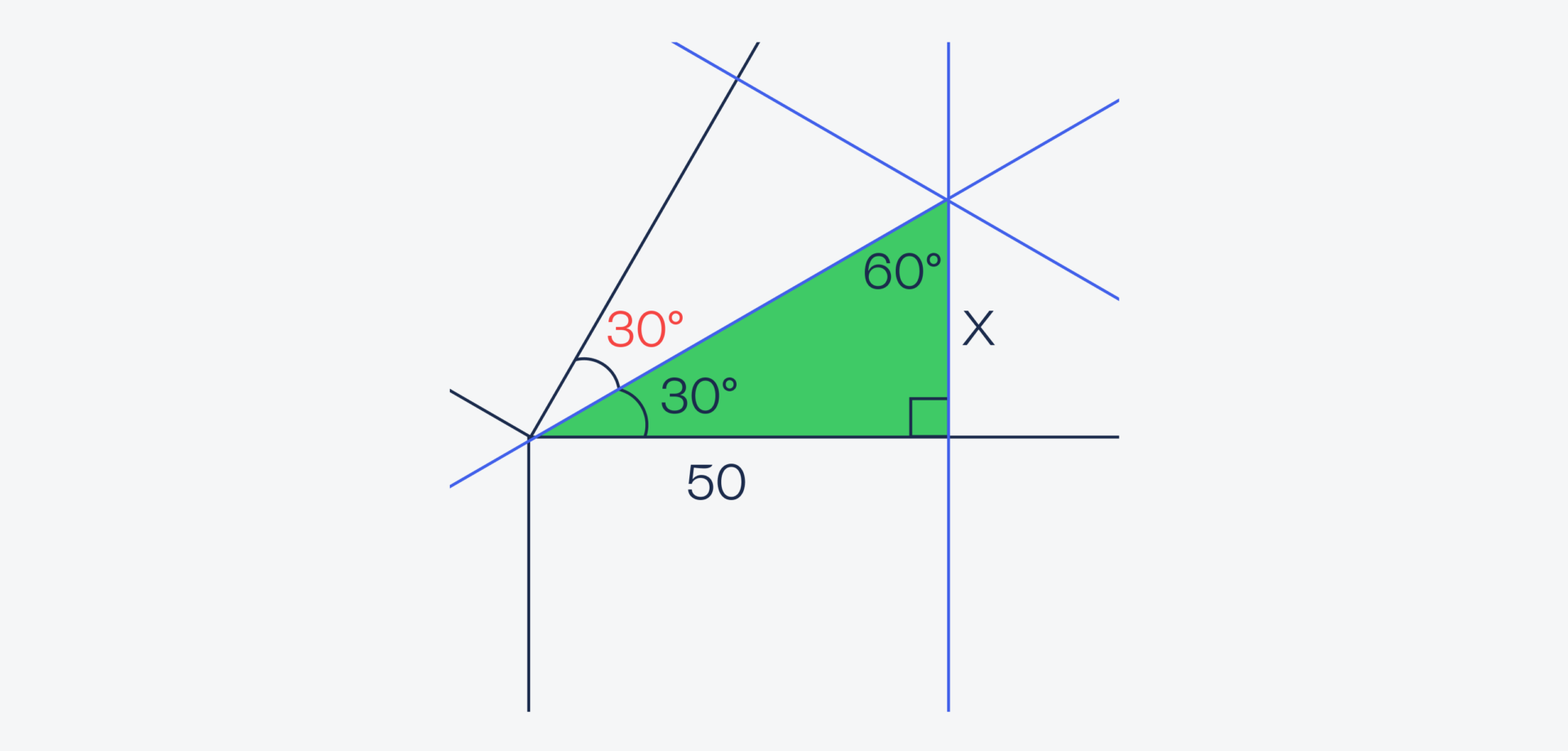
Зная всё это, найдём длину короткого катета по формуле X = tg(30) × 50 = 1/√3 × 50 = 50/√3
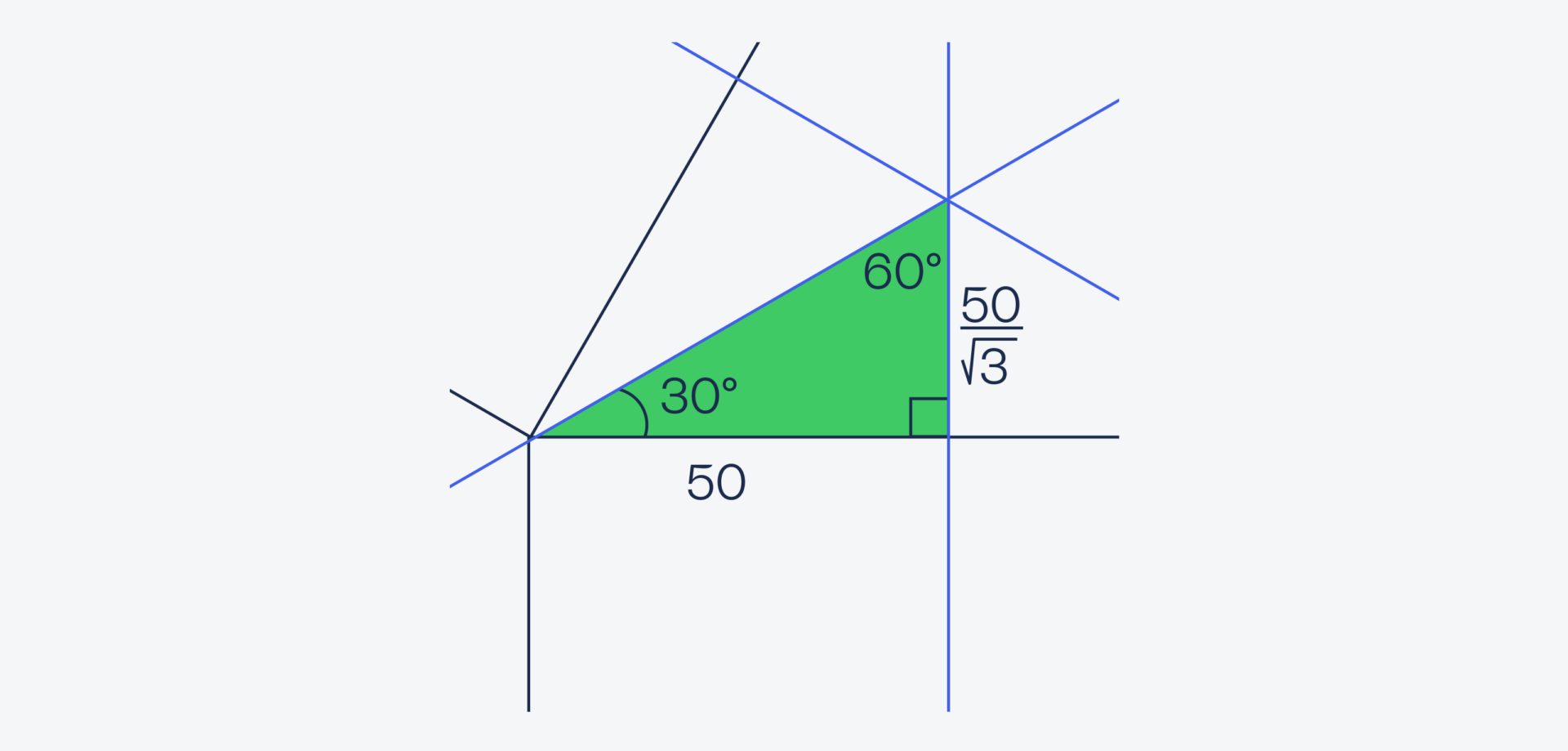
Теперь вернёмся ко всему рисунку и посмотрим на другой треугольник, где одна из сторон — это радиус круга.
Мы уже знаем, что синие линии делят квадраты пополам, а значит, нижняя сторона треугольника равна 50 метрам. Также мы знаем, что внизу у нас прямой угол, а значит, зелёная сторона треугольника тоже равна 100 метрам:
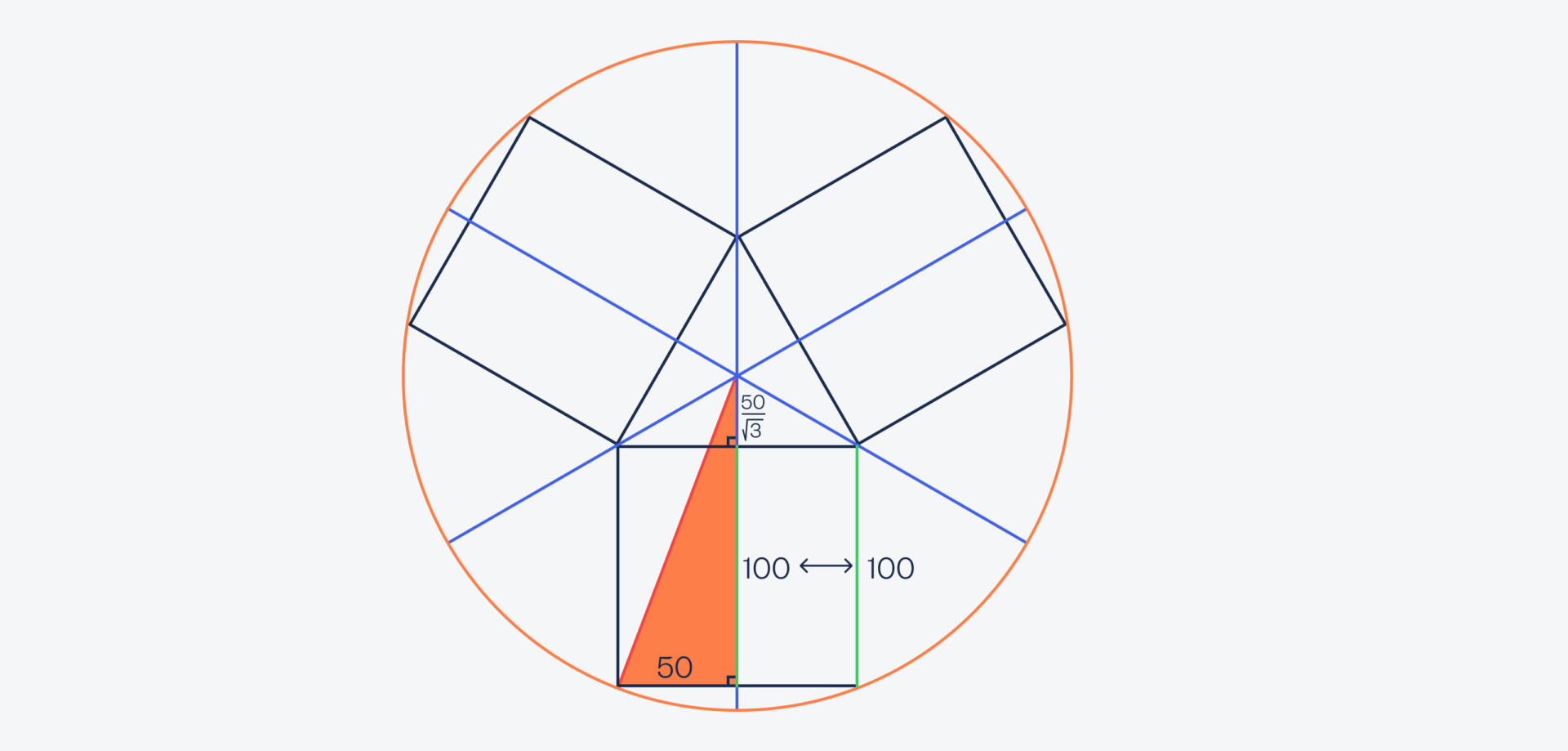
Получается, что у нас есть прямоугольный треугольник с катетами 50 метров и (100 + 50/√3) метров, и нужно узнать длину гипотенузы. По теореме Пифагора сумма квадратов катетов равна квадрату гипотенузы:
a² + b² = c²
Подставим сюда наши значения и решим уравнение:
50² + (100 + 50/√3)² = r²
r = √(50² + (100 + 50/√3)²)
r = √(2500 + (100 +28,86)²) = √(2500 +16606,83) = 138,22
Выходит, что радиус круга (138 метров), который граничит со всеми участками, меньше, чем радиус действия роутера (130 метров). Значит, братьям нужно брать роутер помощнее или ставить всё своё оборудование ближе к роутеру.
Задача про треугольник и неполные размеры
Задачка на логику и геометрию, как в школе. Это не нужно в ИТ, но иногда нужно отвлекаться.
Вот картинка, тут всё понятно. Нужно найти площадь треугольника.
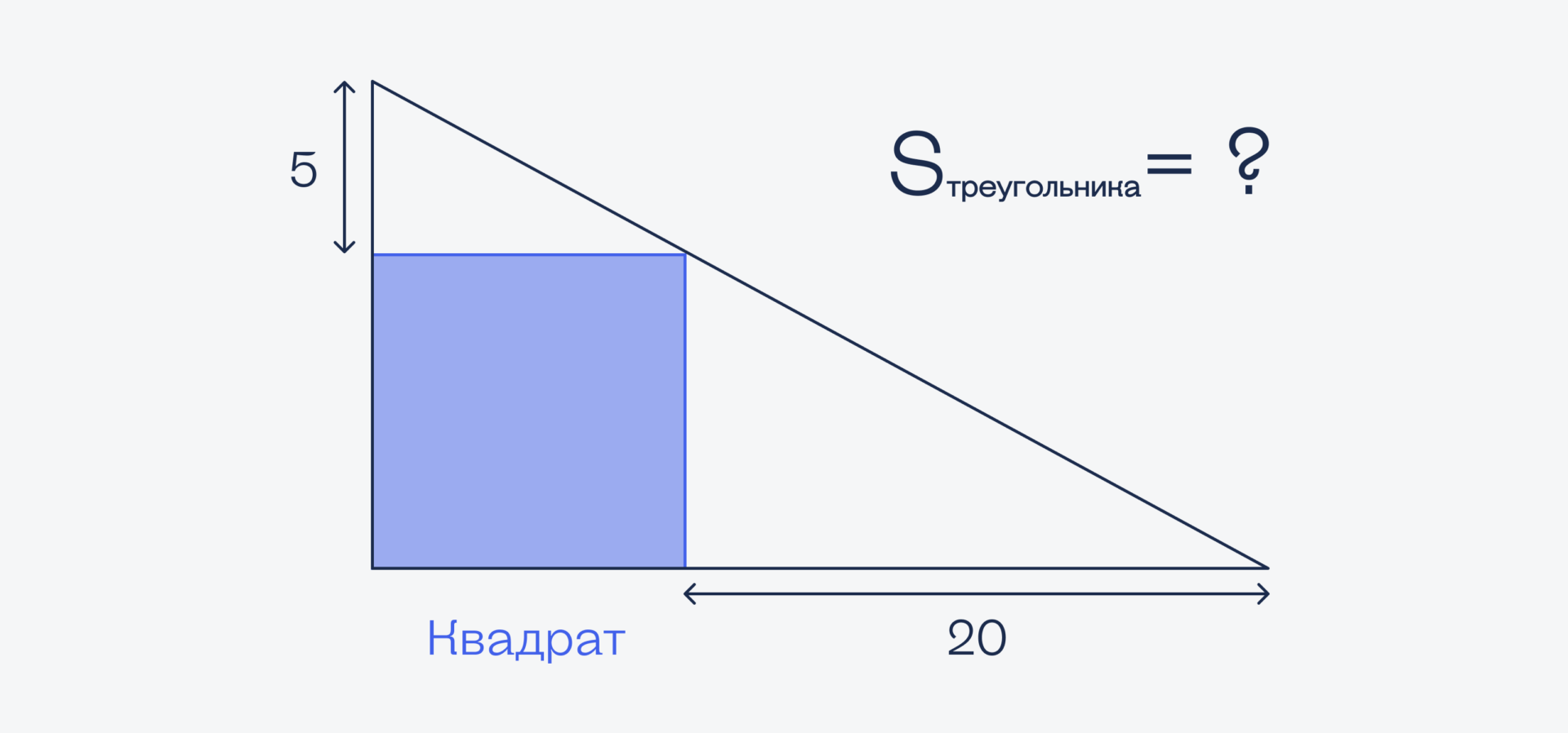
Так как у нас в треугольник вписан квадрат, это значит, что обе его стороны находятся под прямым углом к основанию треугольника:
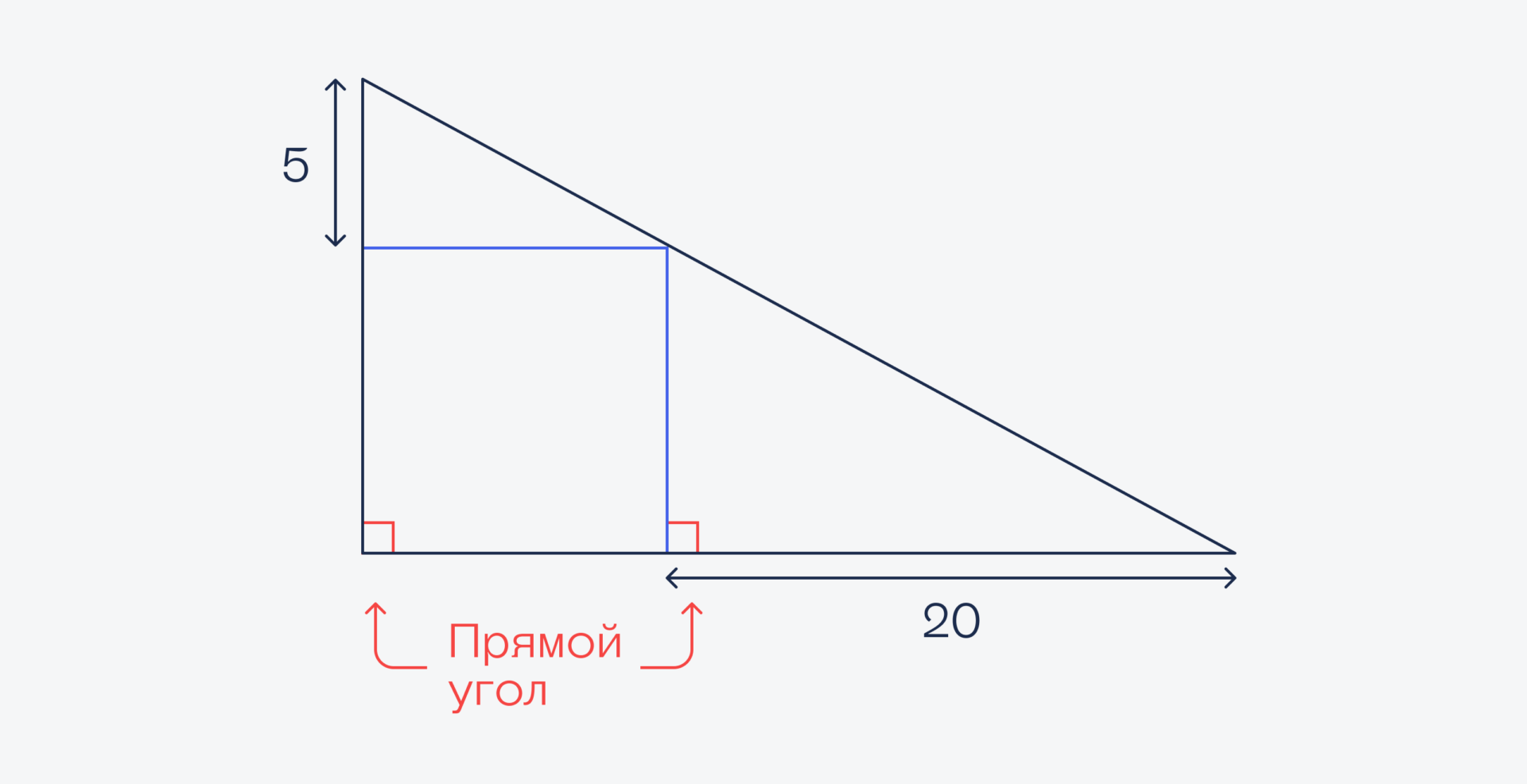
А раз так, то угол, который образуется при пересечении наклонной линии, совпадает с углом наклона этой линии к основанию:
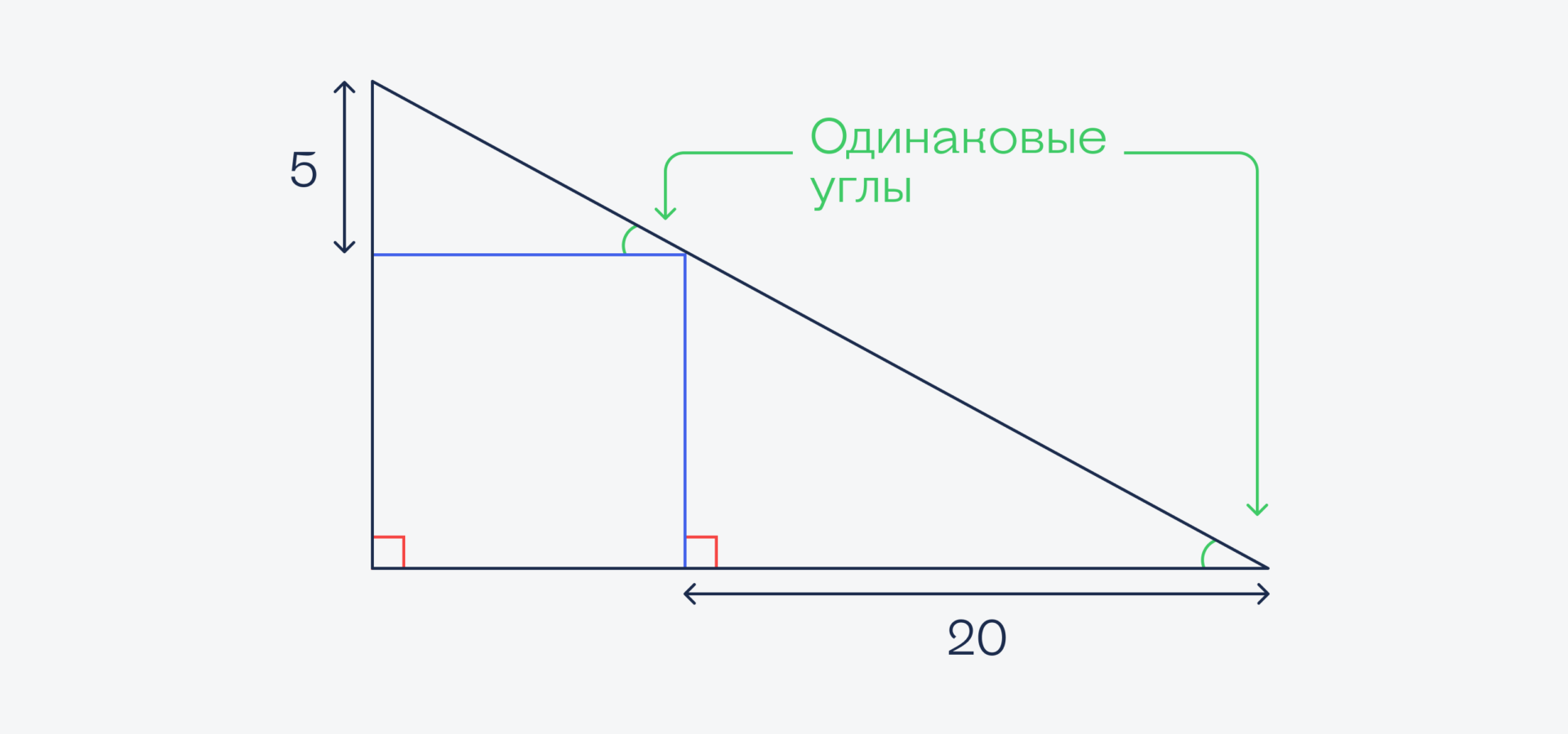
Если у треугольников есть два одинаковых угла, то такие треугольники называются подобными. А раз они подобные, то и соотношение сторон у них будет одно и то же. Обозначим сторону квадрата за X:
Теперь построим соотношение:
5 / X = X / 20 ← решим это уравнение
X² = 5 × 20 = 100
X = 10
Зная сторону квадрата, можно легко найти площадь всего треугольника:
(5 + 10) × (10 + 20) / 2 = 15 × 30 / 2 = 255
Представим, что мы ничего не знаем про тригонометрию, углы и подобие треугольников. Возьмём наш рисунок и мысленно достроим его до прямоугольника:
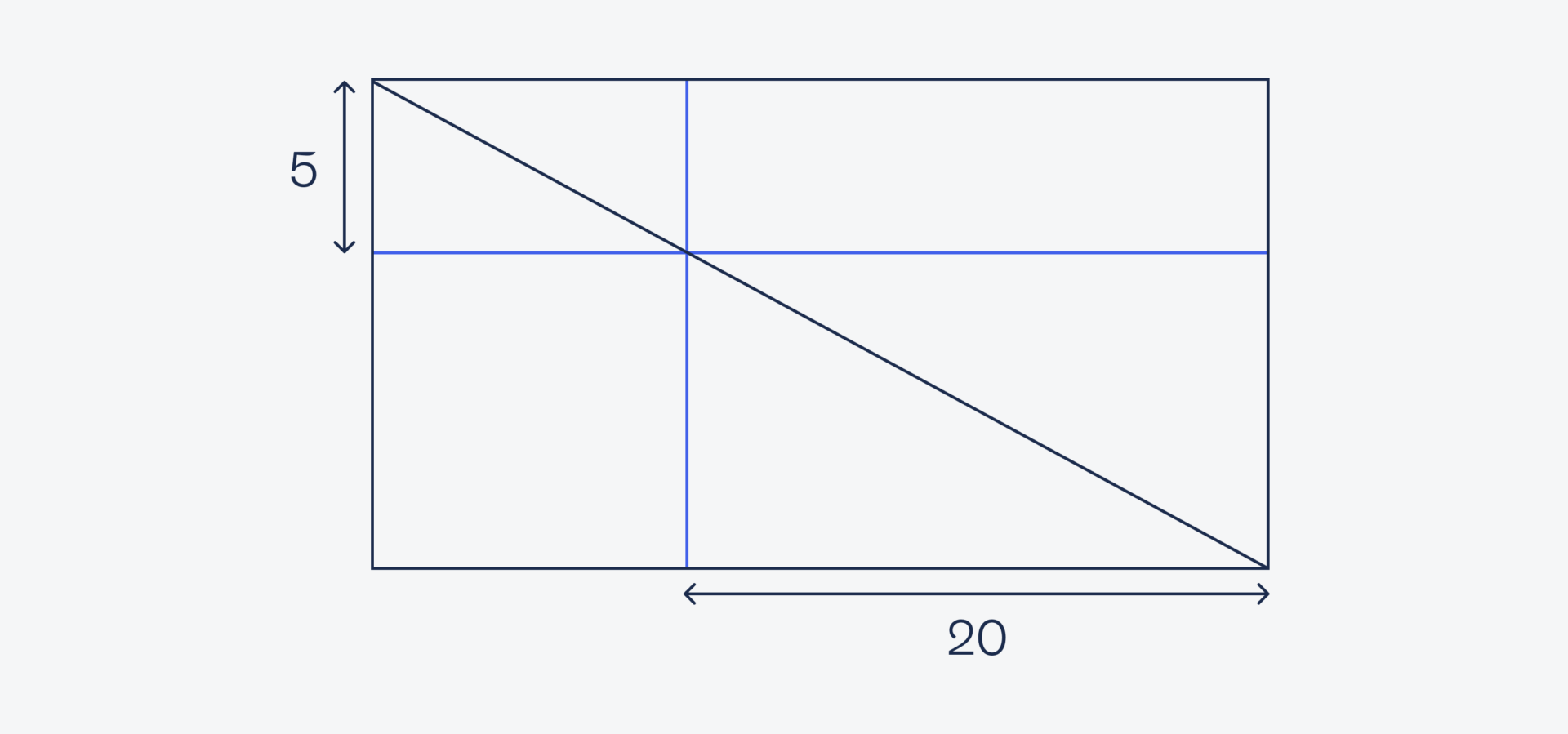
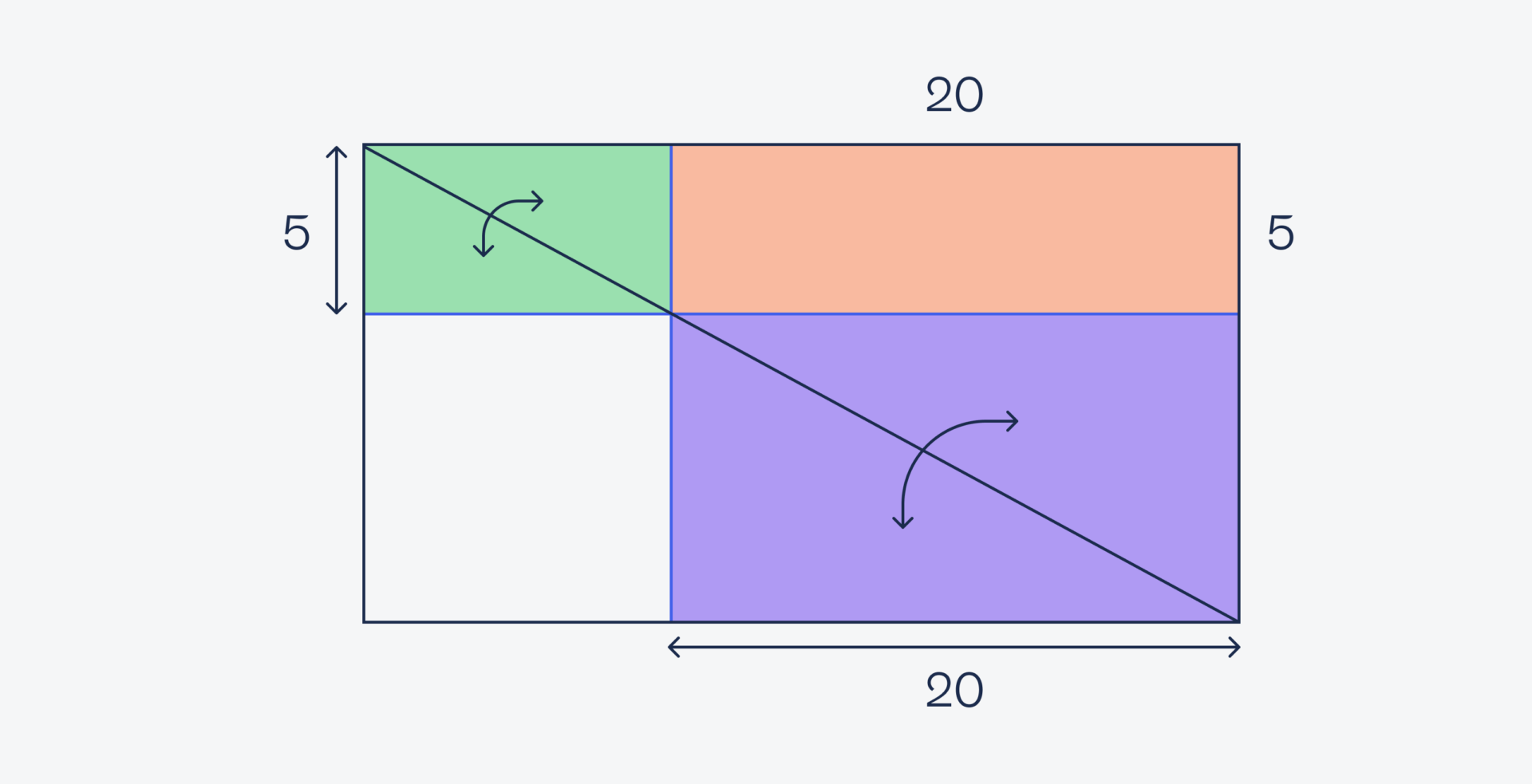
Так как у квадрата все углы прямые, то и синие линии у нас тоже пересекаются под прямыми углами между собой и с внешним прямоугольником. Это значит, что мы можем перенести известные размеры на оранжевый прямоугольник:
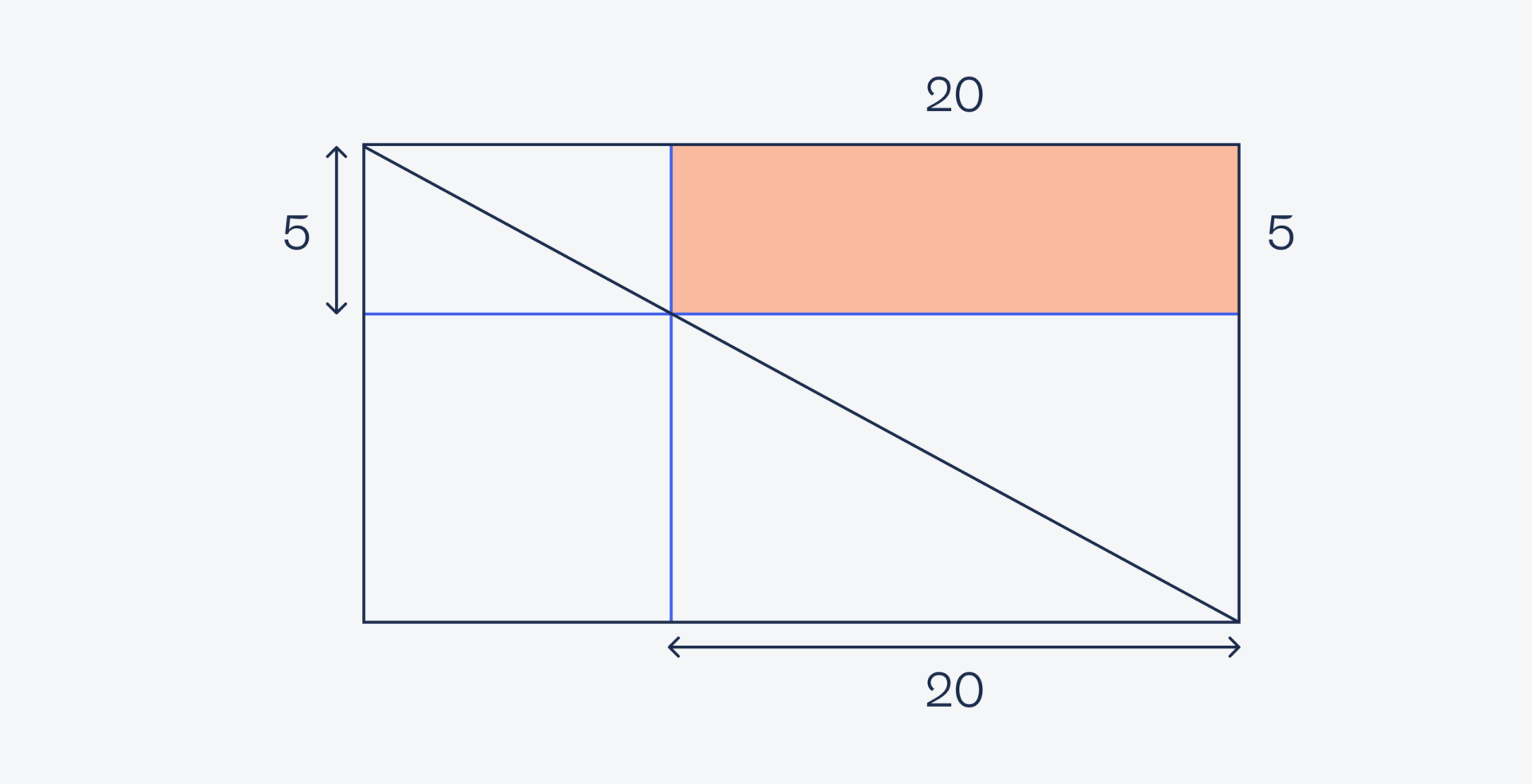
Зная длину и ширину, посчитаем его площадь — 5 × 20 = 100.
Теперь посмотрим на рисунок так: у нас есть прямоугольник, разделённый пополам по диагонали. Это значит, что площадь нижних треугольников совпадает с площадью верхних треугольников:
Но раз у нас часть площадей в верхнем и нижнем треугольнике одинаковая, их можно вычесть из обеих частей:
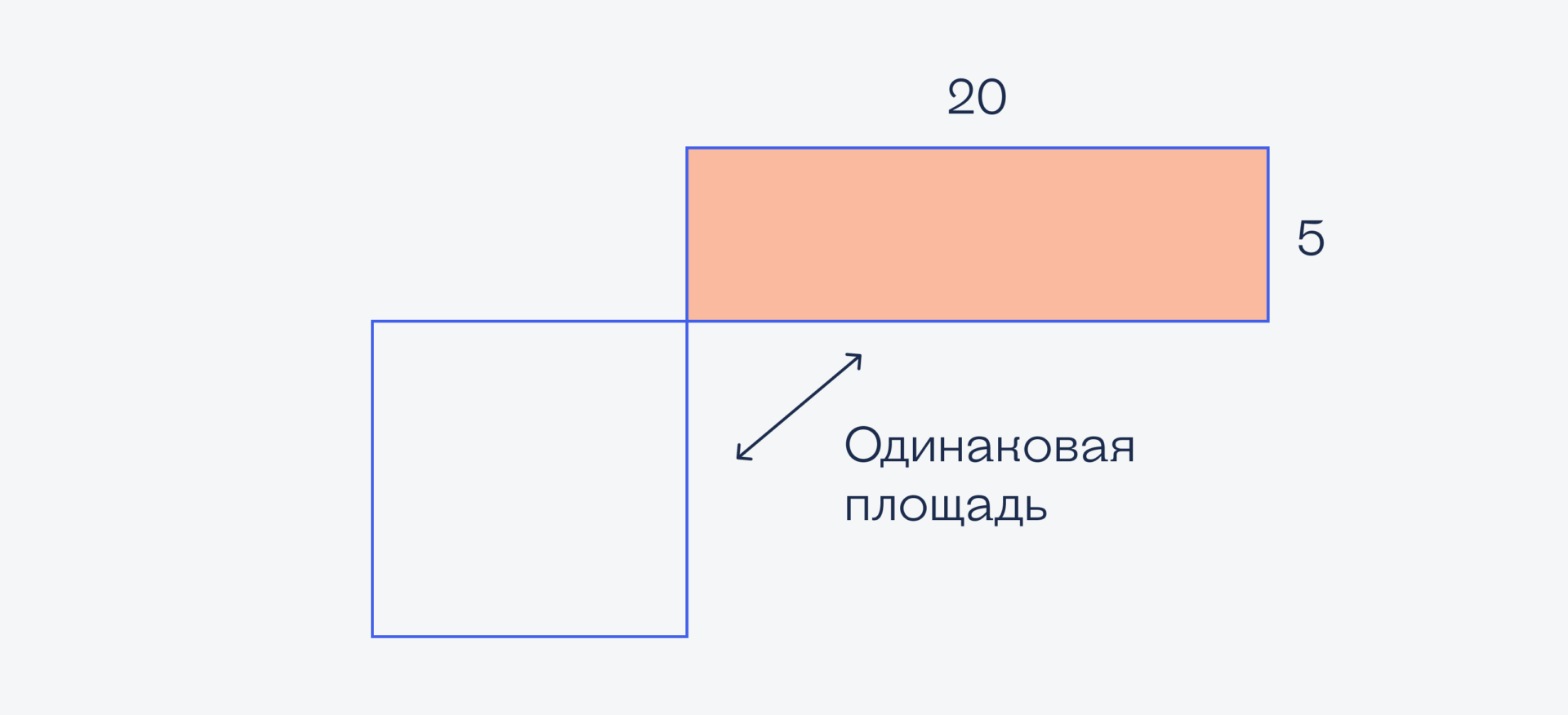
Получается, что площадь оранжевого прямоугольника совпадает с площадью квадрата. А мы знаем, что площадь прямоугольника равна 100; получается, чтобы найти сторону квадрата, нужно извлечь квадратный корень:
√100 = 10
Значит, сторона квадрата равна 10. Этого достаточно, чтобы посчитать всю площадь треугольника:
(5 + 10) × (10 + 20) / 2 = 15 × 30 / 2 = 255
Непростая задача про диагональ квадрата
Если вы уже окончили школу, попробуйте решить эту задачку в уме, используя формулу длины диагонали квадрата:
d = X√2,
где X — это длина стороны квадрата.
Теперь условия: есть квадрат с длиной стороны x. Из нижнего левого угла провели под каким-то углом линию длиной 12 сантиметров:
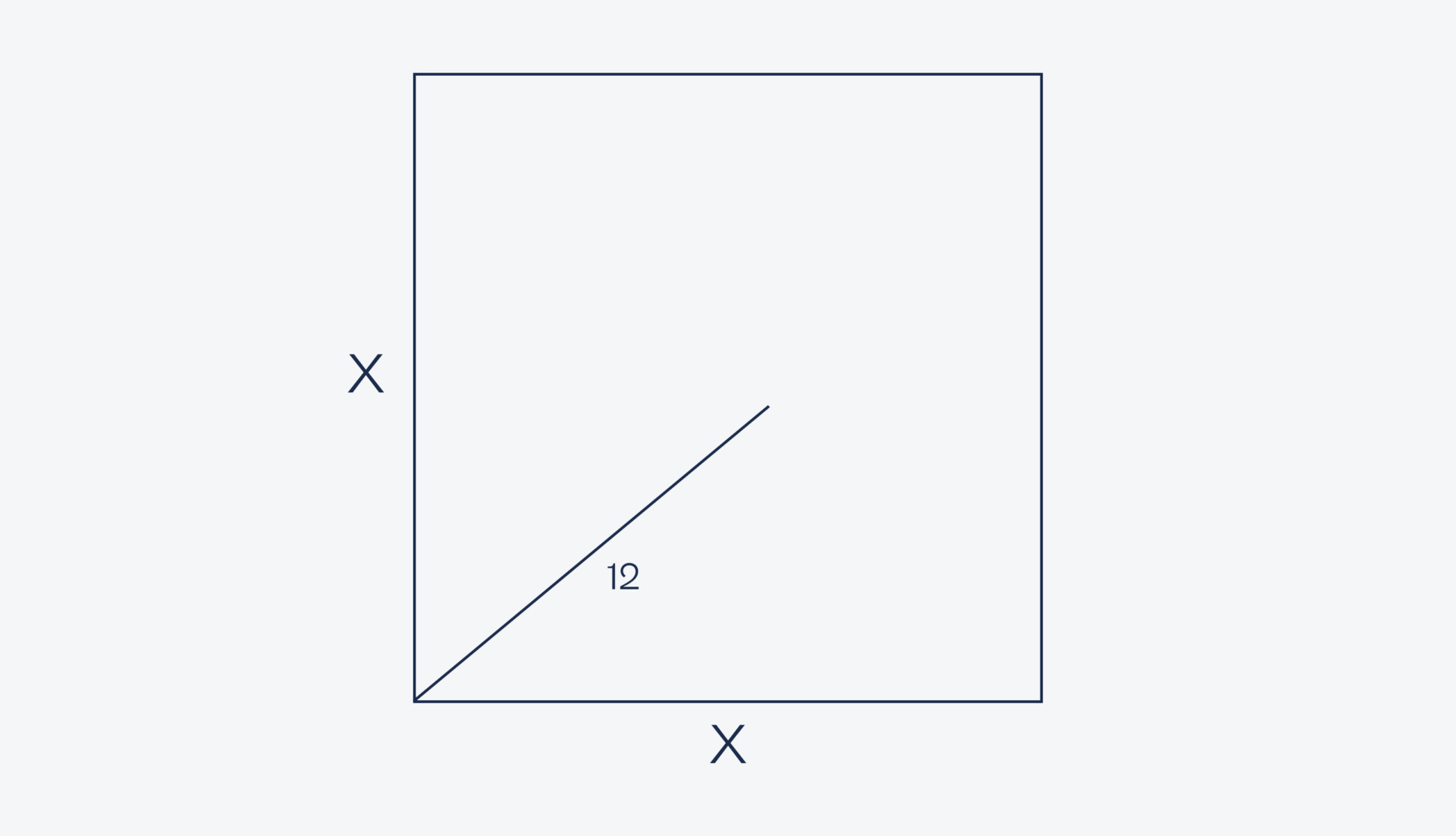
После этого повернули на 90 градусов и провели вторую линию длиной 3 сантиметра:
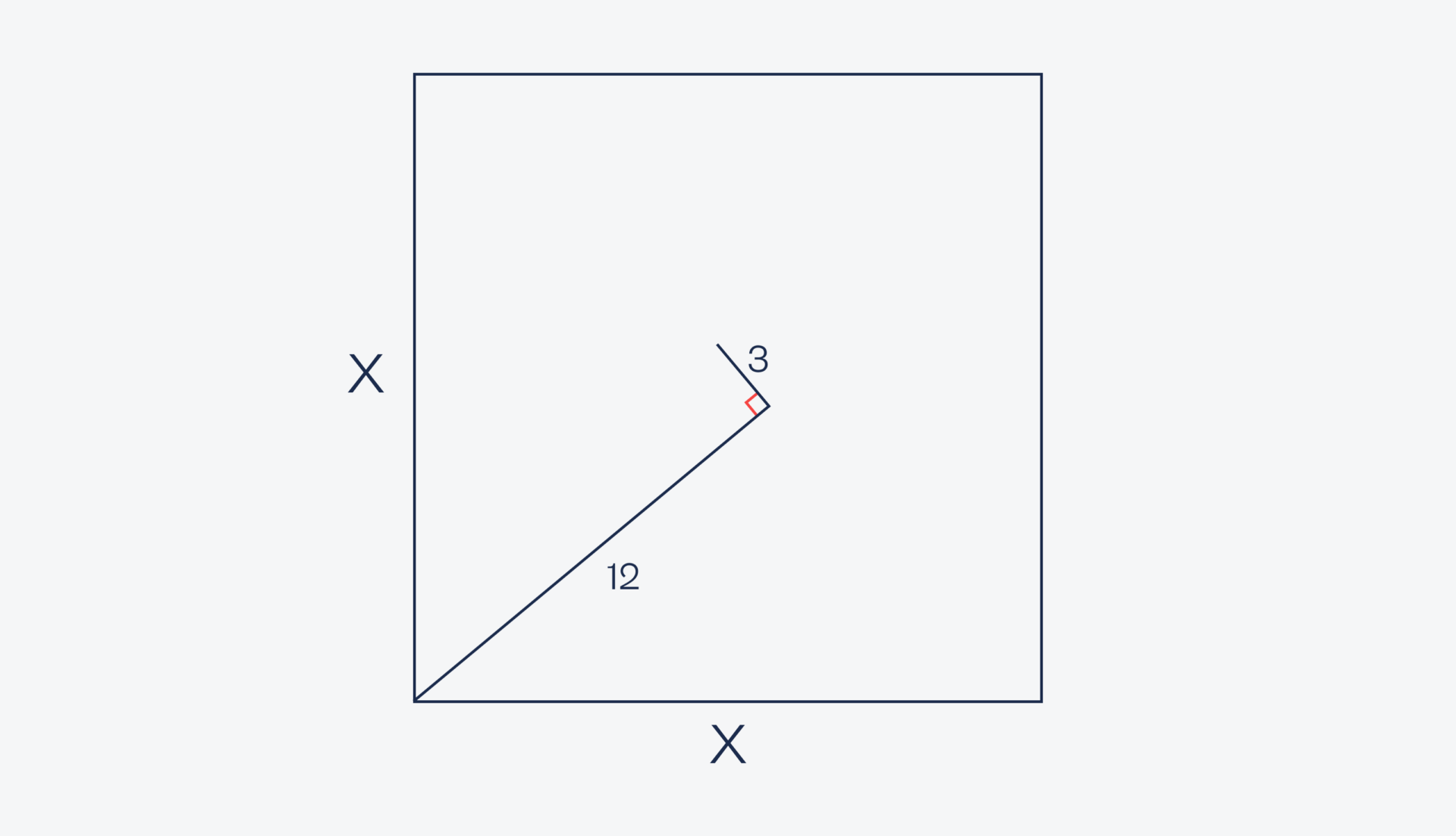
А потом повернули ещё на 90 градусов и провели линию точно до правого верхнего угла. Её длина оказалась равна 9 сантиметрам:
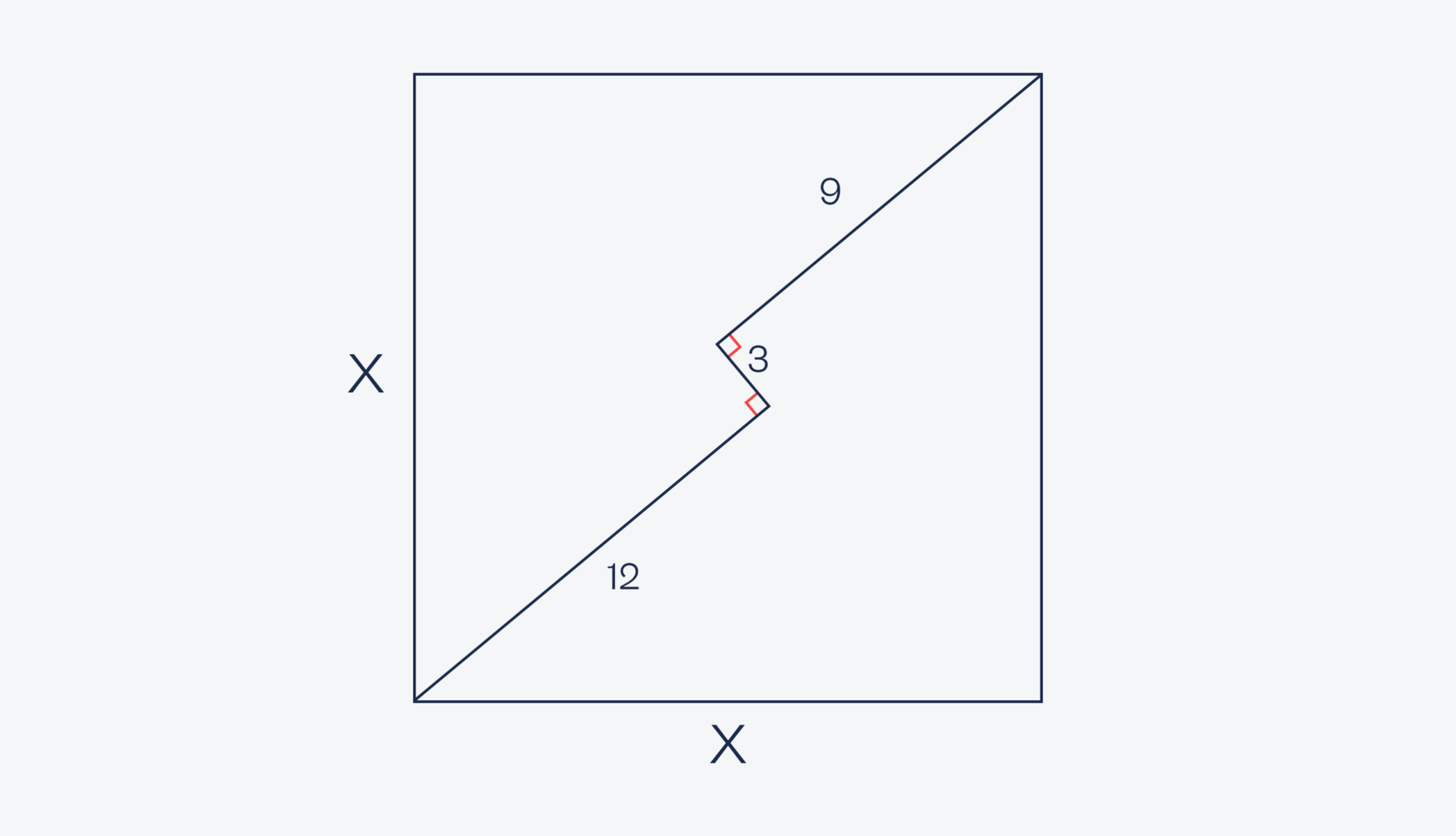
Нужно найти X, то есть длину стороны квадрата.
Чтобы найти решение, нам придётся выйти за рамки квадрата и использовать свойства перпендикулярных линий и прямых углов.
Возьмём два отрезка, 9 и 12 сантиметров и на противоположных концах тоже под прямым углом построим отрезки по 3 сантиметра:
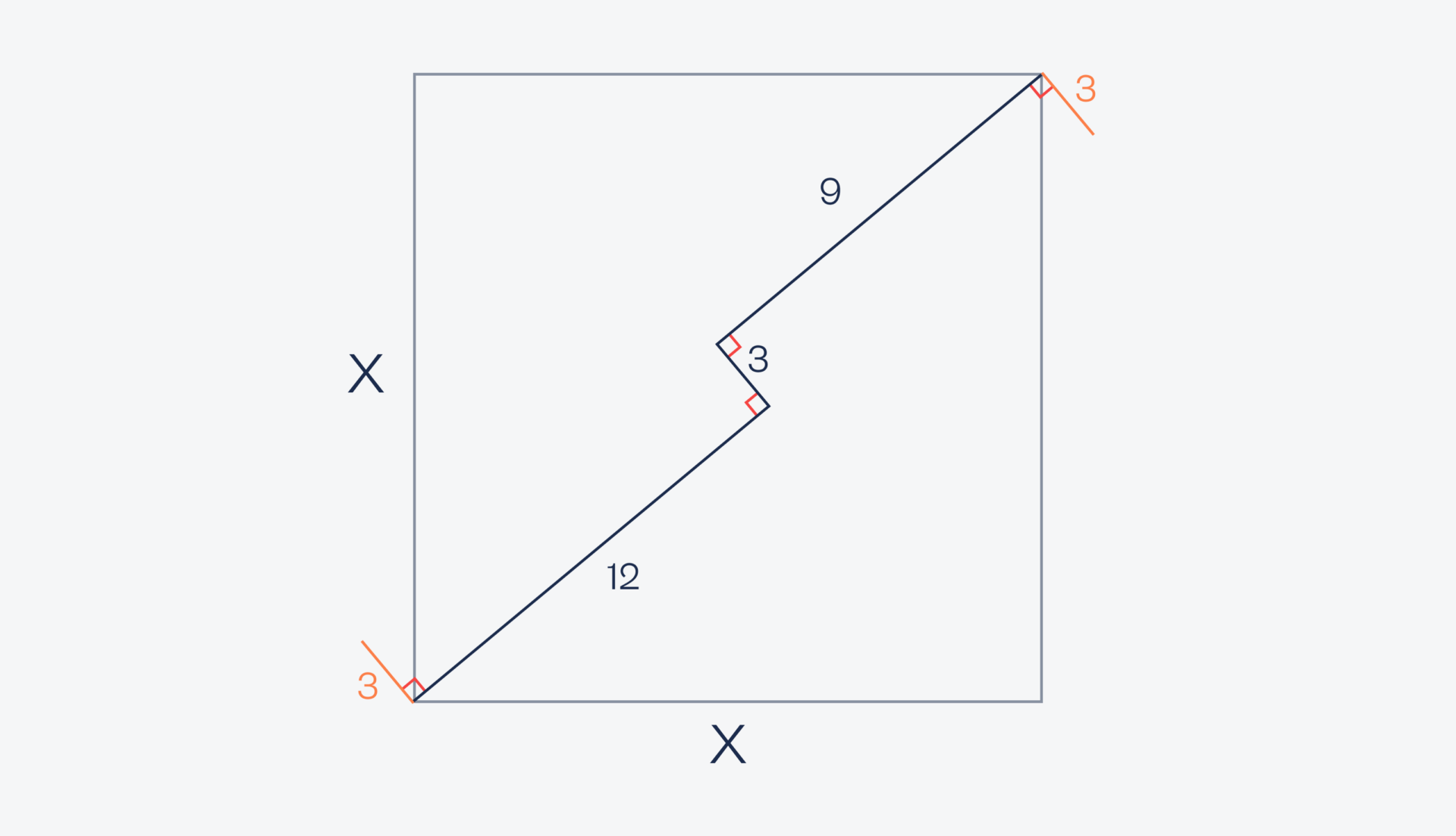
Теперь достроим недостающие линии в каждом прямоугольнике — 9 и 12 сантиметров — и тоже под прямым углом. Так как везде получились углы по 90 градусов, то перед нами два прямоугольника с общей стороной 3 сантиметра:
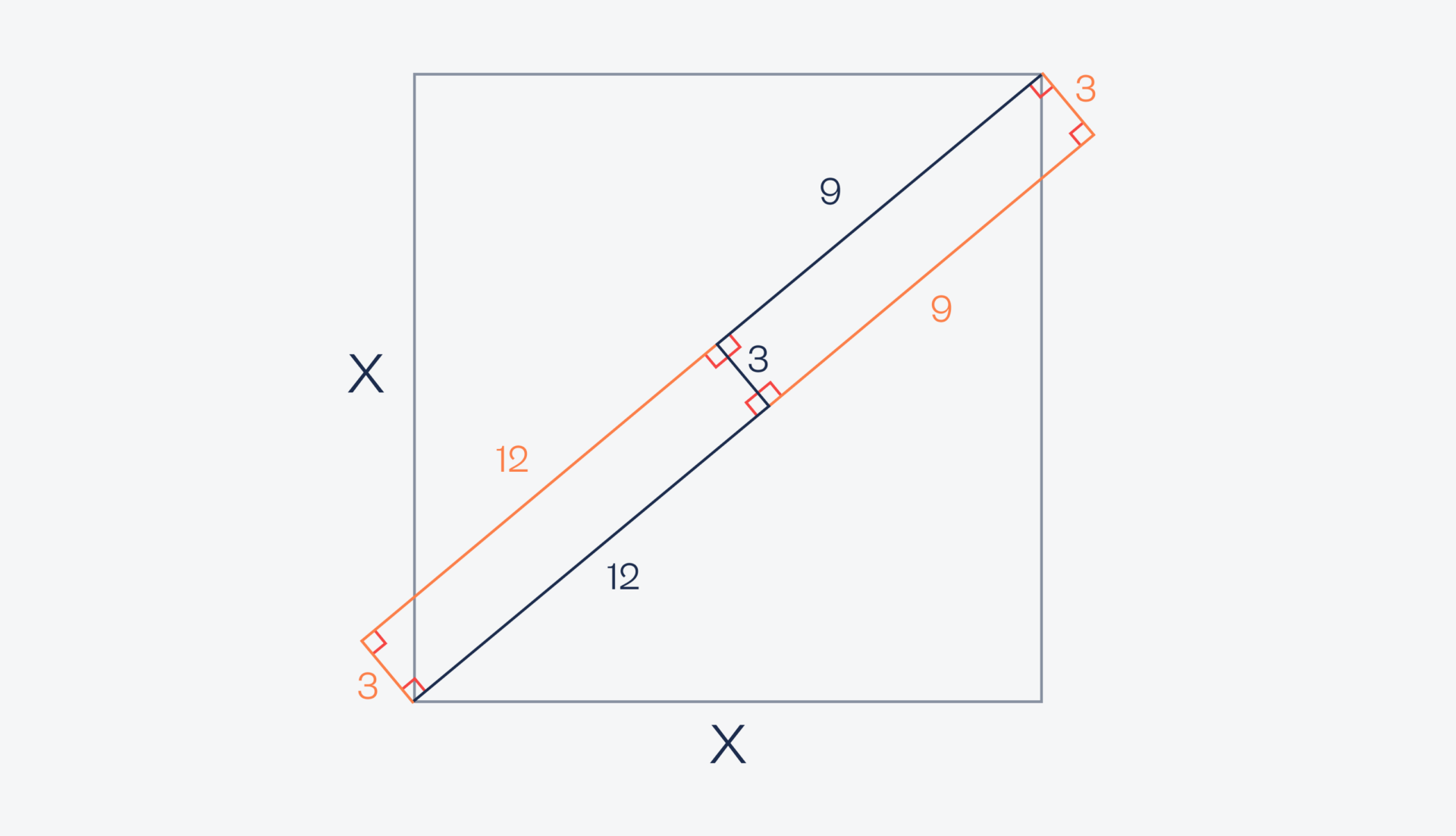
Если их объединить, то у нас получится прямоугольник длиной 9 + 12 = 21 сантиметр и шириной 3 сантиметра. Проведём диагональ в этом прямоугольнике:
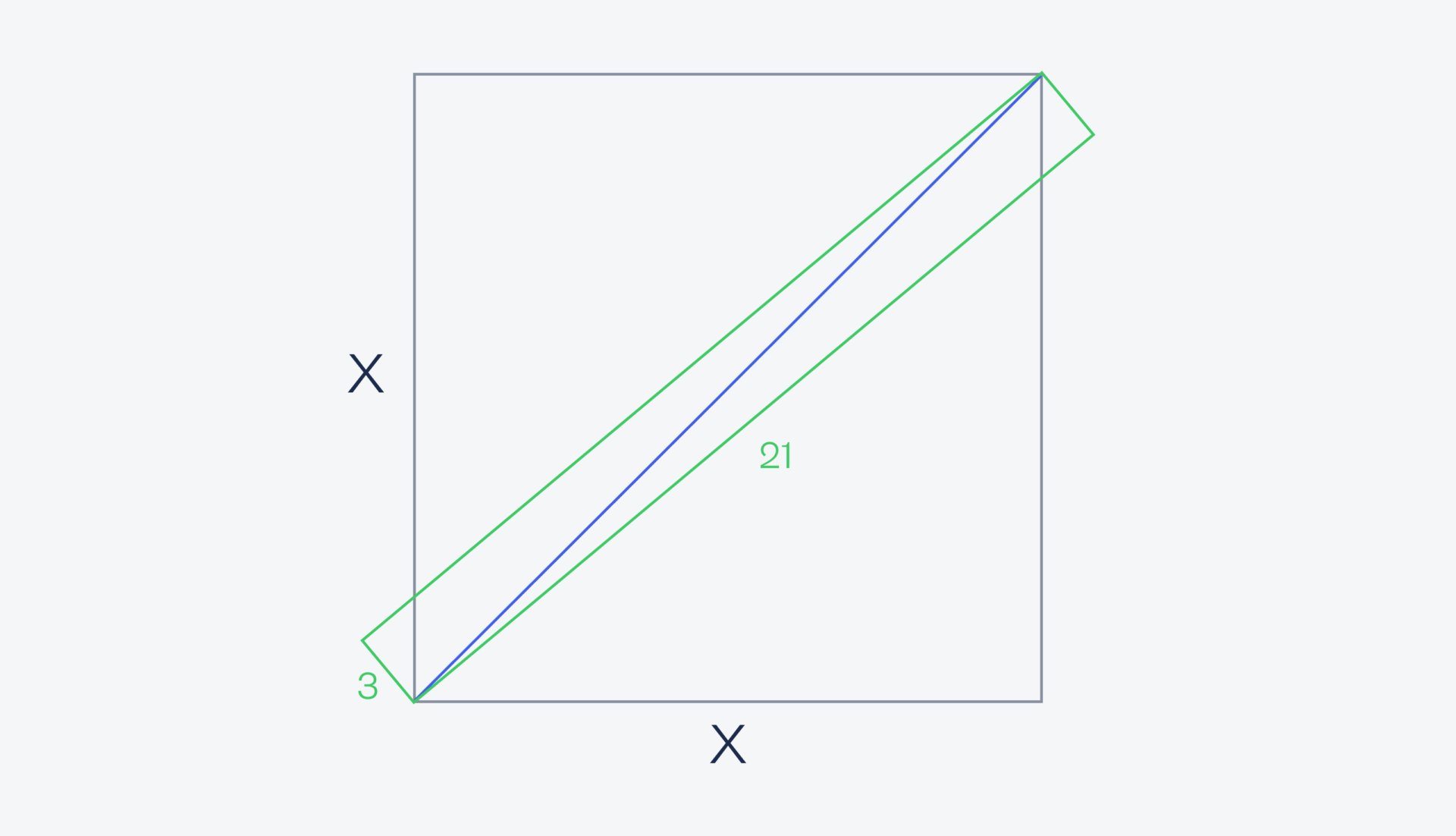
А теперь важное замечание: так как углы прямоугольника совпадают с углами квадрата, то диагональ прямоугольника — это диагональ квадрата и их длины равны. По теореме Пифагора a² + b² = c² найдём диагональ:
21² + 3³ = с² → 441 + 9 = с² → с² = 450
с = √450 = 15√2
Тут нам пригодится формула длины диагонали квадрата: с = X√2. Но у нас c = 15√2, получается, что X = 15 — это и есть длина стороны квадрата.