Все мы с детства знаем, что 2 + 2 = 4. Но что если мы сможем доказать, что 2 + 2 = 5?
Итак, следите за руками, всё по правилам математики.
Добавим к левой части ноль:

Теперь представим этот ноль как разность двух дробей:

Возведём разность четвёрки и дроби в квадрат и сразу извлечём оттуда корень, чтобы получилось в итоге одно и то же:
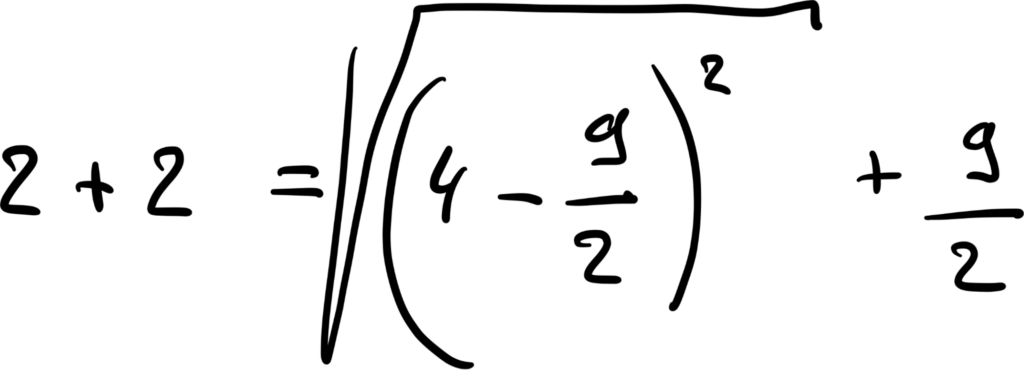
Раскроем скобки под корнем по правилам математики — (a + b)² = a² + 2ab + b²:
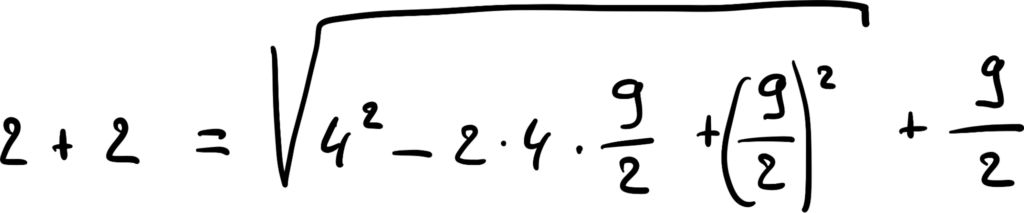
Продолжим вычисления под корнем:
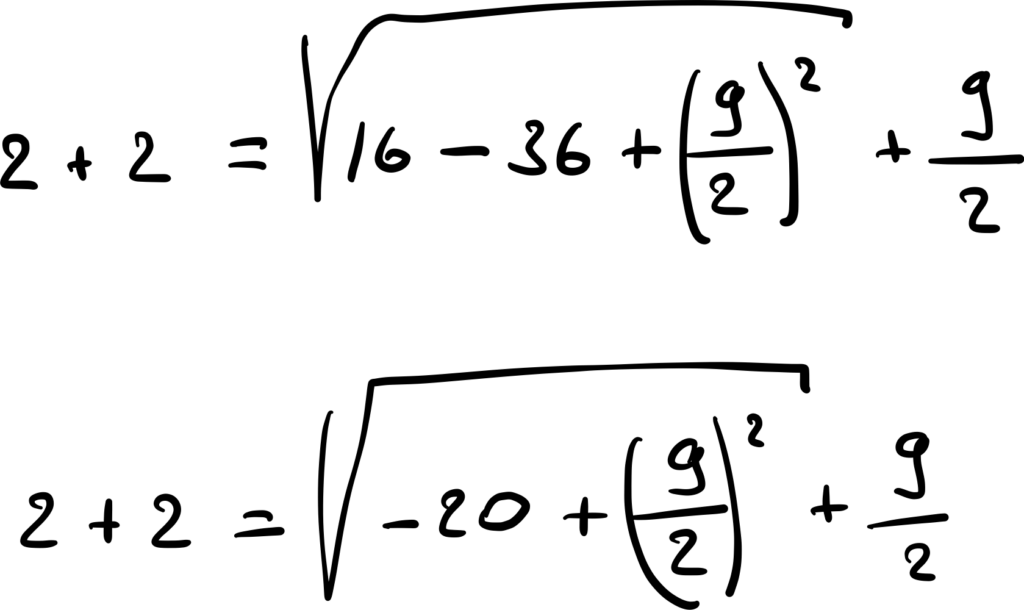
Представим −20 как (25 − 45):
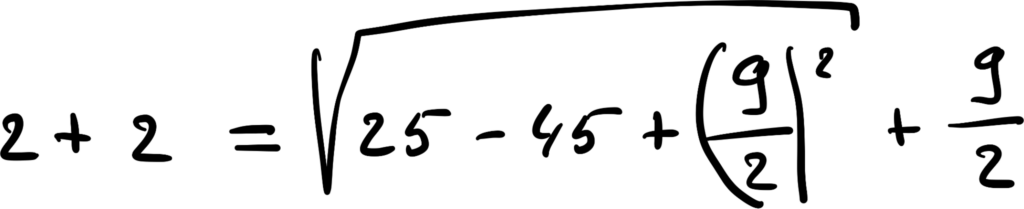
Теперь у нас под корнем получилась развёрнутая разность квадратов, которую можно собрать обратно:
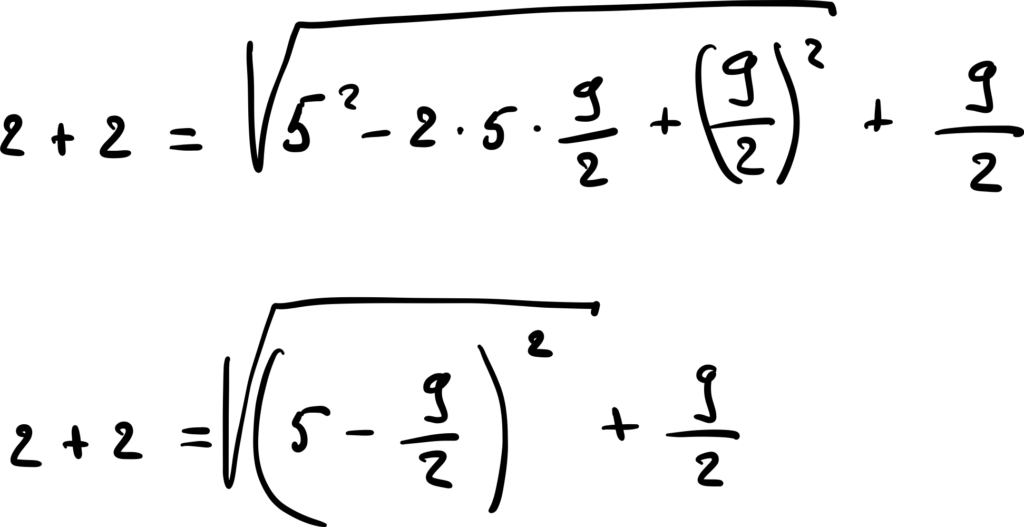
Сокращаем корень и квадрат:
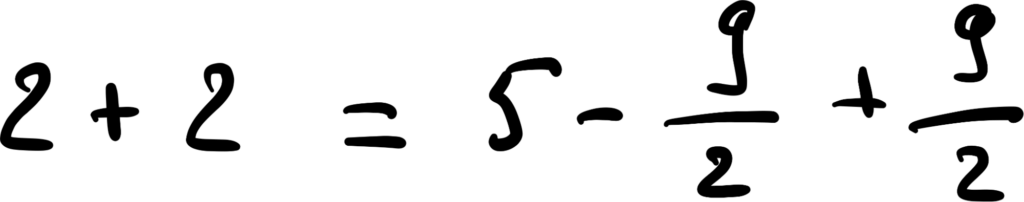
Сокращаем взаимно дроби, которые в сумме дают ноль. И в итоге мы только что доказали, что 2 + 2 = 5.
Но так ли это на самом деле? Нет ли тут ошибки?
На самом деле ошибка происходит уже на третьем шаге, когда мы говорим, что число и корень из квадрата этого числа — это одно и то же, но это не так. Смотрите, как это работает на самом деле:
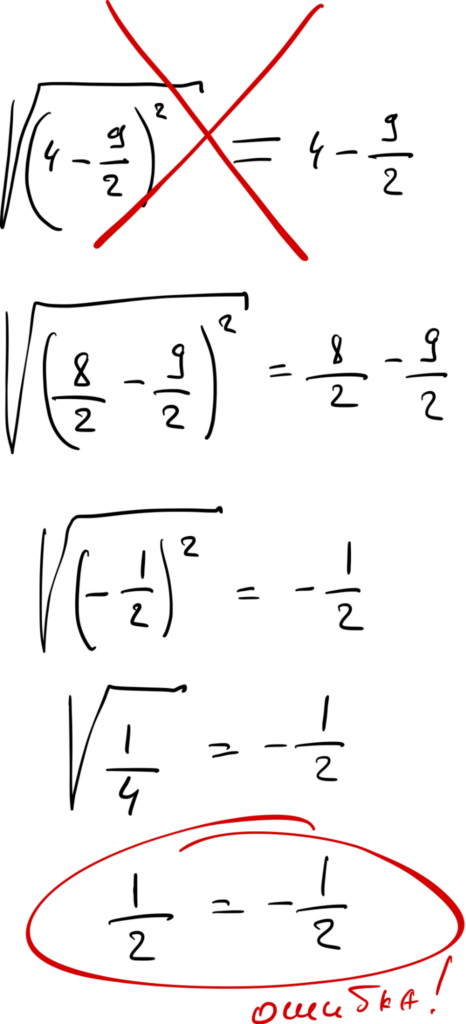
Если говорить про правило извлечения корня из квадрата, то оно звучит так: квадратный корень из квадрата числа равен значению этого числа по модулю! Если изначальное число (а в нашем случае это −½) отрицательное, то корень из квадрата этого числа будет положительным.
Получается, что раз доказательство строилось на неверной предпосылке, то и всё остальное доказательство тоже неверное.
Поэтому расслабляемся: 2 + 2 = 4.