Продолжаем эпопею с алгоритмами для расширения компьютерного кругозора и знаний информатики. Алгоритмы — это область знаний, которая изучает, как правильно организовать какое-то повторяющееся действие, чтобы быстро получать нужный результат. Так как машины глупые и нуждаются в алгоритмах, то чем лучше наши алгоритмы, тем лучше машины.
Мы уже разобрали:
- метод Монте-Карло (про казино и математику);
- метод имитации отжига (про задачу коммивояжёра);
- метод полного перебора (тоже про коммивояжёра, но медленно).
Теперь разберём алгоритм поиска с возвратом. Из понятных вещей, которые он может сделать, — решение судоку любой сложности.
Что такое поиск с возвратом
Есть такие задачи, где нужно перебрать все варианты решения, чтобы убедиться, что мы нашли нужный ответ и ничего не пропустили. Например, когда мы решали кодом задачу Эйнштейна, то в первой версии ждали несколько часов, пока компьютер проверит все перестановки. Это называется полным перебором.
Алгоритм поиска с возвратом тоже относится к полным переборам, но у него есть особенность, которая делает этот перебор проще:
если алгоритм понимает, что идёт по неверному пути, то все остальные варианты в этом пути тоже помечаются как неправильные и алгоритм их не рассматривает.
Получается, что мы перебираем только те варианты, в которых потенциально есть решение, — а это сильно сокращает время перебора даже без специальной оптимизации.
Как это работает в теории
Ключевой элемент поиска с возвратом — рекурсия, то есть функция, которая вызывает сама себя. Работа рекурсии часто требует много оперативной памяти, но из-за особенностей алгоритма памяти нужно гораздо меньше, чем при полном переборе «в лоб».
Алгоритм поиска с возвратом состоит из трёх частей:
- Рекурсия, которая получает очередную комбинацию для проверки и уходит вглубь себя раскладывать это по полочкам.
- Генератор вариантов, который создаёт новую цепочку данных и отправляет их в рекурсию.
- Модуль проверки, который проверяет, идёт ли наша рекурсия по верному пути, и если да — то нашла она решение в итоге или нет.
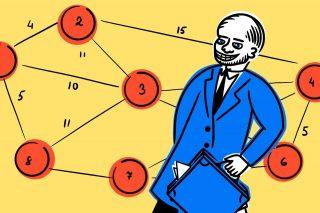 Что такое «задача коммивояжёра»
Что такое «задача коммивояжёра» Решаем задачу коммивояжёра простым перебором
Решаем задачу коммивояжёра простым перебором Как работает доставка товаров в России
Как работает доставка товаров в России Как автомобильный навигатор находит самый быстрый путь
Как автомобильный навигатор находит самый быстрый путь Метод Монте-Карло — один из самых полезных алгоритмов в ИТ
Метод Монте-Карло — один из самых полезных алгоритмов в ИТ Что такое отжиг и зачем его имитировать
Что такое отжиг и зачем его имитировать Красиво расставляем 8 ферзей на доске
Красиво расставляем 8 ферзей на доскеПример, как это работает
Представим, что у нас есть самолёт, который может летать по таким рейсам в аэропортах, и нам нужно составить самую длинную цепочку рейсов:
DMO → SVO
BZK → TYA
VKO → DMO
TYA → VKO
Если визуализировать работу алгоритма, то можно увидеть, как он строит возможные цепочки для перебора и отбрасывает те, где условия явно не выполняются. При этом алгоритм не заходит внутрь неправильных цепочек, а оставляет только те, в которых комбинации удовлетворяют начальным условиям.
Вот как может выглядеть часть работы этого алгоритма:
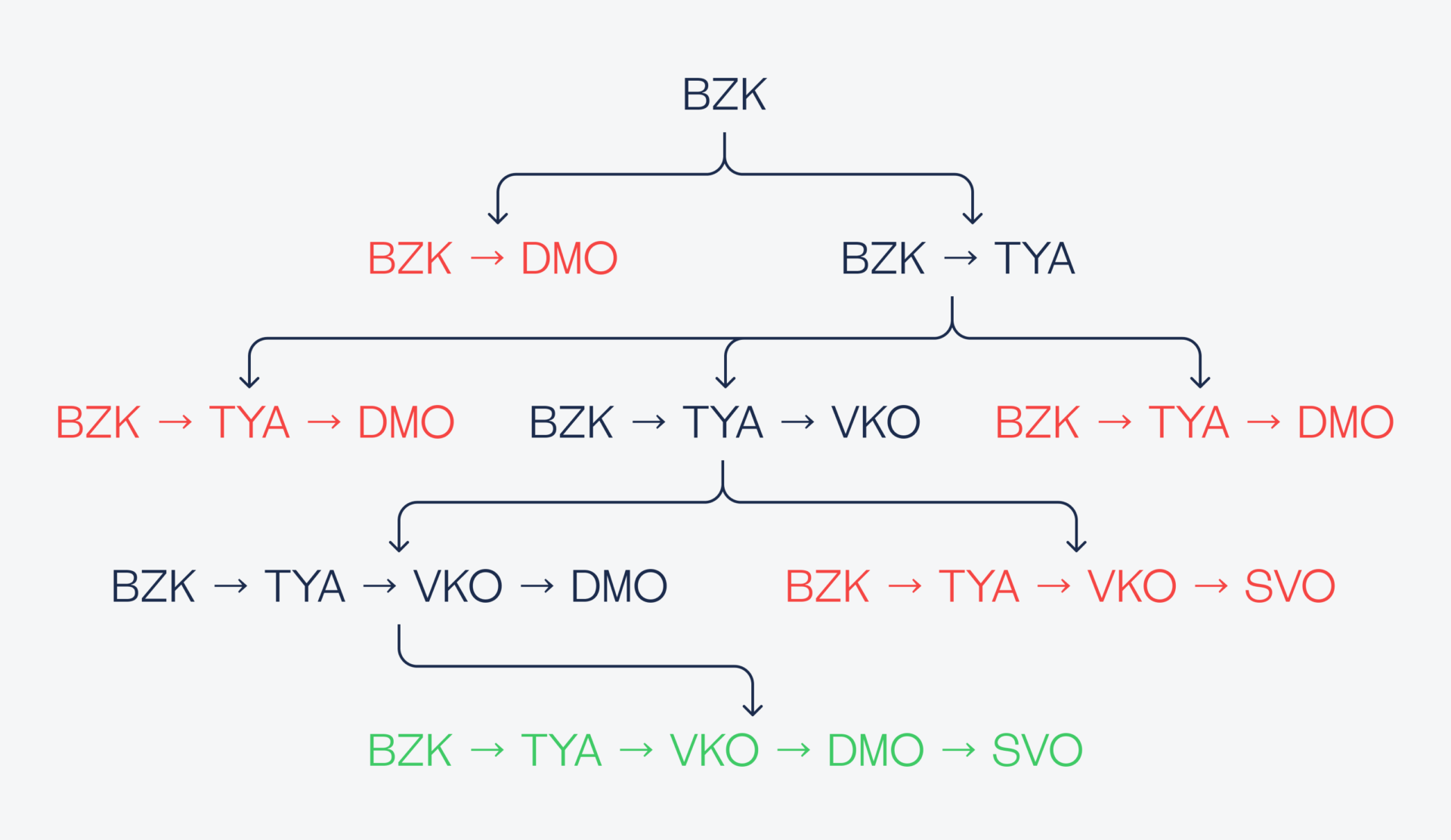
Где этот алгоритм применяется в жизни
Поиск с возвратом применяется в задачах комбинаторной оптимизации, например:
- для синтаксического анализа естественной речи, когда компьютеру нужно разложить текст на лексические составляющие, подобрать ответ, а потом поставить слова в ответе в правильном и естественном порядке;
- для поиска решений в задачах «про наполнение рюкзака», когда нужно найти, например, оптимальное соотношение веса, объёма и цены;
- в языках логического программирования — Prolog или Planner, которые используют этот алгоритм для создания ответов на запросы пользователя;
- для решения логических задач и пазлов, например судоку:
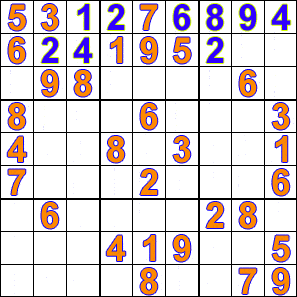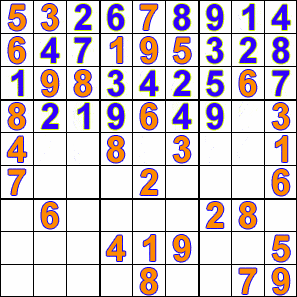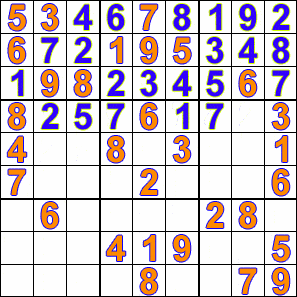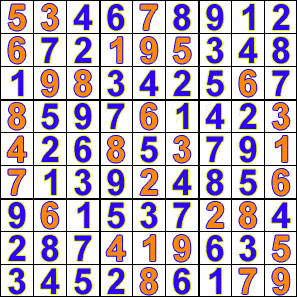
Что дальше
В следующем подходе напишем генератор судоку и решатель судоку. Потому что судоку — это хорошо.