Продолжаем рассказывать о разных формулах и подходах из математики, которые часто применяются в ИТ и в привычных алгоритмах. Сегодня будет про бином Ньютона — про него много кто слышал, но не все представляют, что это и зачем это нужно. Сейчас разложим по полочкам.
Чтобы понять бином Ньютона, нам понадобится треугольник Паскаля.
Что такое треугольник Паскаля
Треугольник Паскаля — это одно из названий треугольной таблицы чисел. Его назвали в честь математика Блеза Паскаля, но про такой треугольник математики знали тысячу лет назад.
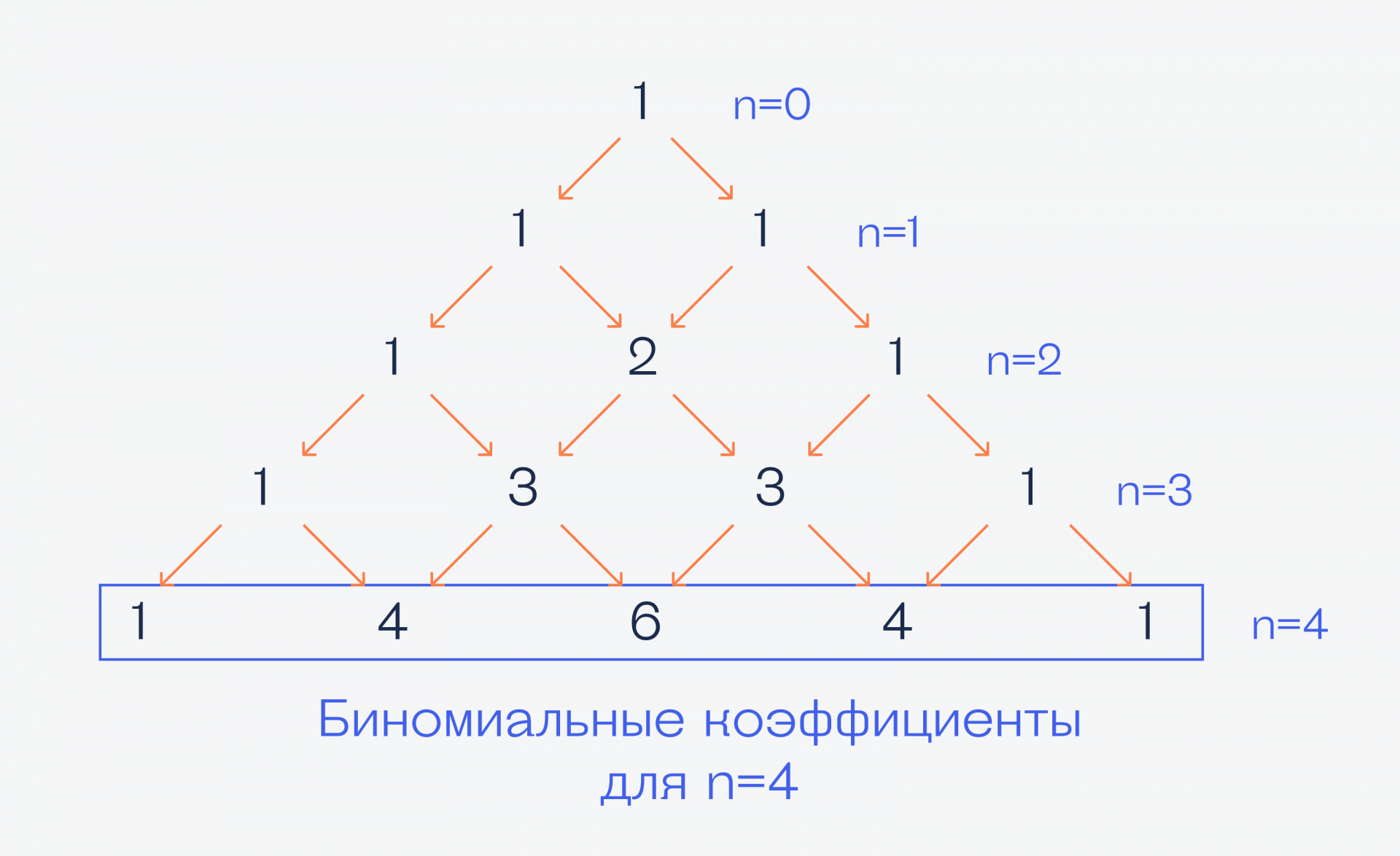
Работает треугольник так: берём единицу (это будет вершина треугольника), а все остальные числа в каждом ряду получаем сложением левых и правых чисел, которые стоят выше. Если нарисовать, то получится так:
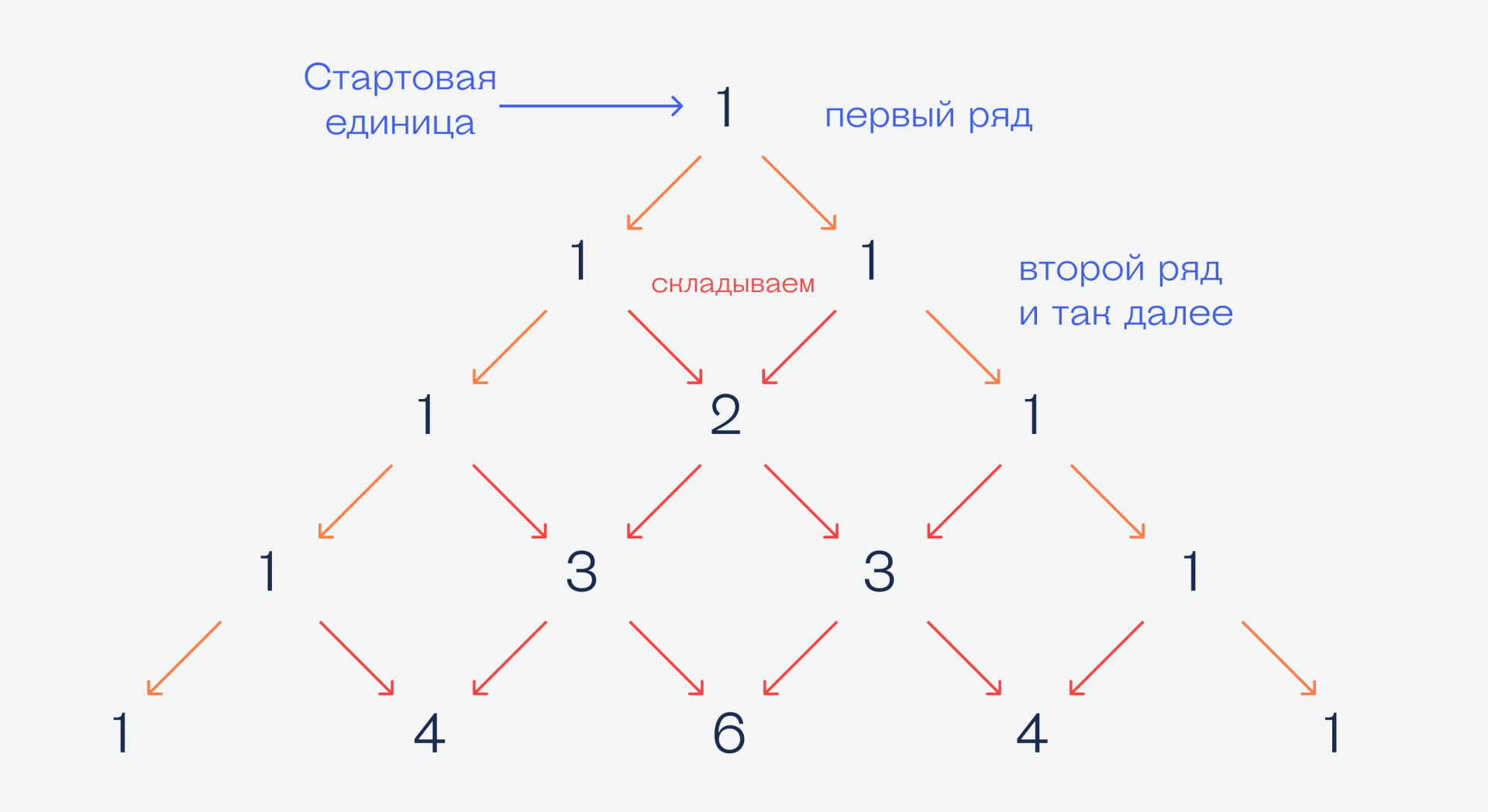
Такой треугольник можно продолжать бесконечно. В математике этот треугольник обладает разными полезными свойствами, но нам он нужен для биномиальных коэффициентов в биноме Ньютона. Вот теперь поговорим про бином.
Что такое бином Ньютона (простыми словами)
Бином Ньютона — это формула, которая помогает посчитать сумму двух чисел, возведенную в какую-то степень.
Разбираем по полочкам:
- У нас есть некие числа a и b. Мы не знаем какие, потому что алгебра.
- Не зная, что это за числа, мы их складываем.
- Эту сумму почему-то очень хочется возвести в какую-то степень — в квадрат, в куб, в четвертую, хоть в девятьсот девяносто девятую — алгебре плевать на ваши чувства.
- Нам нужна формула, как это сделать. Вот эта формула и есть бином Ньютона.
Из школьной программы мы помним такую формулу: (a + b)2 = a2 + 2ab + b2 — это частный случай бинома Ньютона для квадрата суммы.
Может быть, вы помните сумму в кубе: (a + b)3 = a3 + 3a2b + 3ab2 + b3 — это тоже бином Ньютона.
А что если нам нужно возвести сумму не в квадрат, не в куб, а в сто сорок шестую степень? Какая тогда будет формула? Вот для этого нам нужна более обобщенная формула, которая опишет вообще все варианты биномов для любой степени.
Вот как эта формула выглядит в общем виде:
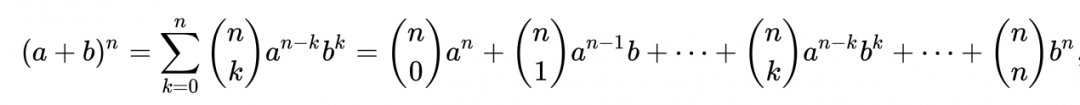
Про знак Σ мы уже говорили — это обозначение суммы, а цифры в больших скобках — это биномиальные коэффициенты. В общем виде они считаются так:
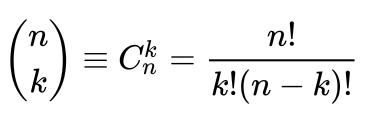
Исходя из этой адской формулы для расчета бинома на компьютере нам нужно будет много раз посчитать факториал — это произведение всех целых чисел от единицы до заданного числа. Например, 5! = 1 × 2 × 3 × 4 × 5 = 120. А факториалы в силу своей цикличности жрут довольно много оперативной памяти. Может так получиться, что мы не сможем посчитать коэффициенты бинома, потому что закончилась оперативка.
Как посчитать бином Ньютона
Чтобы не одуреть от количества расчётов факториалов, возьмём простой бином третьей степени: (x + y)³. Теперь посчитаем коэффициенты:
- Первый коэффициент самый простой: у нас n = 3, а k = 0, потому что так записано в формуле. Факториал ноля равен единице, а 3 − 0 = 3, поэтому результат будет такой: 3! / 3! = 1.
- Второй уже сложнее: n = 3, k = 1, поэтому (n − k) будет равно двум — (3 − 1) = 2. Теперь разделим факториалы: 3! / (1! × 2!) = 6 / 2 = 3.
- Третий тоже интересный: n = 3, k = 2, поэтому (n − k) будет равно единице — (3 − 2) = 1. Теперь разделим факториалы и не забудем про то, что надо учесть ещё k! в знаменателе: 3! / (2! × 1!) = 6 / 2 = 3.
- Четвёртый будет считаться так: : n = 3, k = 3, поэтому (n − k) будет равно нулю — (3 − 3) = 0. Теперь разделим факториалы и не забудем про то, что надо учесть ещё k! в знаменателе: 3! / (3! × 0!) = 6 / (6 × 1) = 1.
Теперь разберёмся со степенями:
- Для первого слагаемого нам нужно возвести икс в степень (3 − 0) = 3, а игрек — в степень 0 (и это будет равно единице). Получаем x³.
- Второе слагаемое: возводим икс в степень (3 − 1) = 2, а игрек — в степень 1 . Получаем x²y.
- Третье: возводим икс в степень (3 − 2) = 1, а игрек — в степень 2 . Получаем xy².
- И четвёртое: возводим икс в степень (3 − 3) = 0, а игрек — в степень 3 . Получаем y³.
Наконец, добавляем коэффициенты и получаем итоговый результат разложения бинома Ньютона:
(x + y)³ = x³ + 3x²y + 3xy² + b³
Но, оказывается, необязательно считать факториалы — есть способ проще.
Биномиальные коэффициенты и треугольник Паскаля (простая теория в картинках)
Тут нам приходит на помощь треугольник Паскаля. Оказывается, числа в каждом ряду — это биномиальные коэффициенты для каждой степени n:
На практике это работает так: допустим, что по ходу работы алгоритма нам нужно раскрыть скобки и вычислить (x + y)⁴. Применим сюда бином Ньютона и треугольник Паскаля:
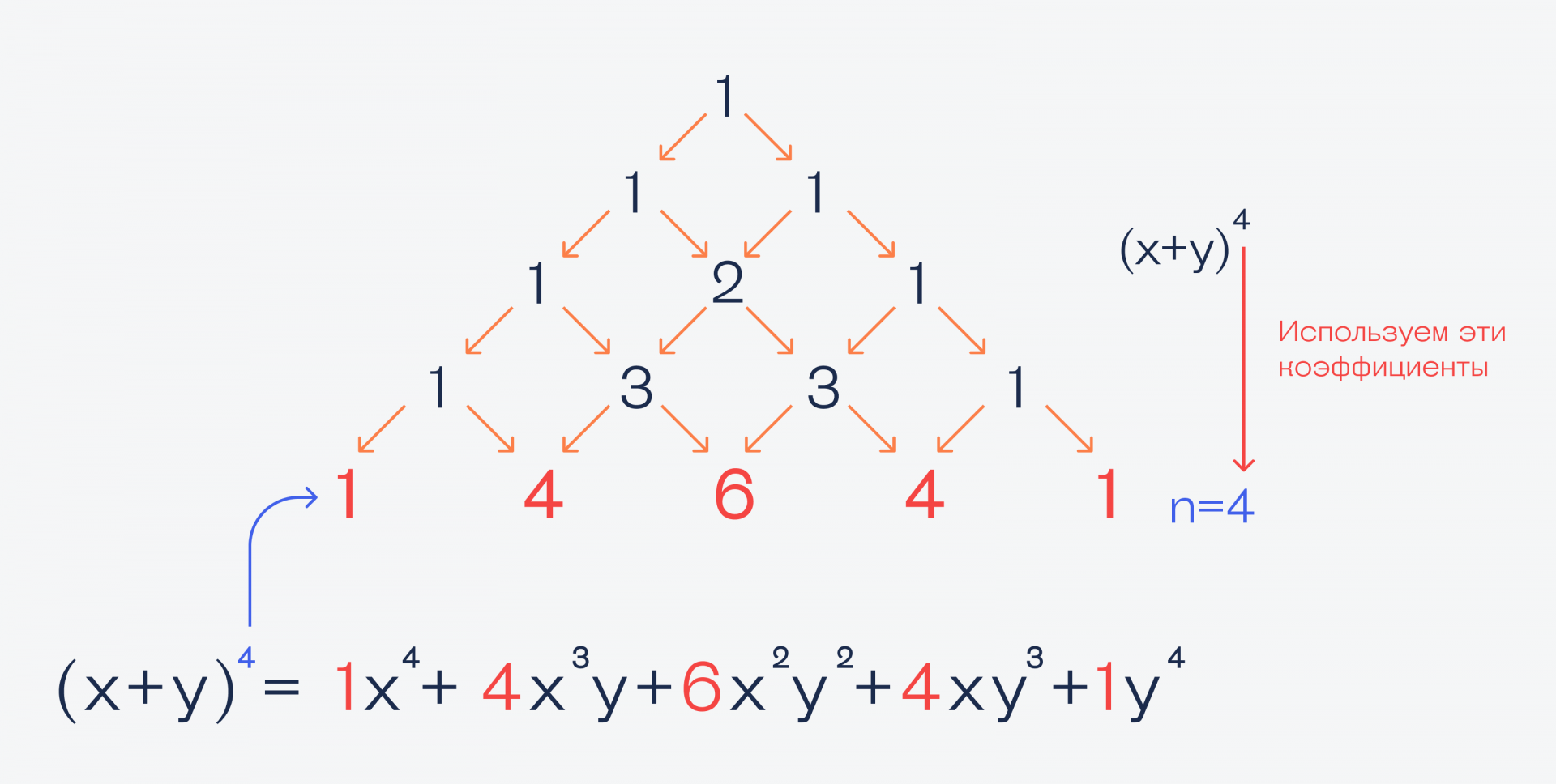
Получается, что с помощью этого треугольника можно не считать все эти формулы с факториалами, а быстро находить нужные коэффициенты, подставлять их в формулу бинома и сразу получать ответ. Так можно разложить любой бином и получить ответ гораздо быстрее, чем вычисляя все факториалы подряд.
Где используется бином Ньютона
Кроме математики, где бином нужен для комбинаторики и разных полезных формул, он часто применяется в программировании. Например, с его помощью можно обойти ограничение на размер оперативной памяти при возведении большого числа в степень: его можно разложить на сумму двух чисел поменьше и посчитать слагаемые через бином.
Также биномиальные коэффициенты часто применяются в матрицах и операциях с векторами — а именно на матрицах построены почти все нейросети. Поэтому если мы сможем быстро находить нужный коэффициент и применять его к матрице, то сможем быстрее создавать дипфейки и генерировать реалистичные пейзажи. Строго говоря, для этого сейчас нужно просто знать команду import, потому что готовых библиотек на эту тему — вагон, без всяких биномов.
А ещё на биномиальных коэффициентах работает отдельная непозиционная система счисления — её применяют в проектах, где надо быстро перебирать много различных вариантов и их возможных сочетаний.
Что дальше
Дальше мы попробуем применить эти знания и алгоритмы на практике: напишем код, который использует бином Ньютона для решения разных хитрых бытовых задач.