На прошлой неделе мы рассказали, что такое логарифм и зачем он нужен. Сегодня найдём логарифм с помощью программирования.
Вот короткая версия теории:
- Логарифм — это в какую степень нужно возвести одно число, чтобы получить другое число.
- То, число, которое возводят в степень, называется основанием логарифма.
- Логарифм обозначается словом log.
- Например, log(10) 100 = 2, потому что 10² = 100.
- Есть ещё обозначение lg — это то же самое, что log(10). И есть ln — это то же самое, что log(e), где e — это число Эйлера, важная математическая константа.
- Логарифмы используются в каждой значимой области нашей жизни, от биологии до физики.
Теперь, когда мы знаем достаточно про логарифм, то можем написать программу, которая нам найдёт любой логарифм по любому основанию.
В чём идея
Мы уже выяснили, что логарифм — это степень, в которую нужно возвести основание логарифма, чтобы получить нужное число. Получается, что нам нужно подобрать такую степень, чтобы при возведении она давала такое же число — это и будет ответом к решению логарифма.
Алгоритм поиска будет таким:
- Найдём минимальное значение степени, возведение в которую ещё не превысит наше число.
- Это значит, что следующее за ним целое число — уже перебор, и основание в этой степени точно превысит наше число.
- Будем делить этот промежуток пополам нужное количество раз, пока не получим нужную точность ответа после запятой.
- Когда цикл закончится, середина оставшегося промежутка и будет ответом.
Мы так уже делили границы пополам в задаче про то, как угадать число за 7 попыток, поэтому, если алгоритм показался немного непонятным, — перечитайте то решение и возвращайтесь сюда.
Готовим переменные
Для работы программы пользователь должен будет указать три вещи:
- Основание логарифма.
- Число, от которого мы берём этот логарифм.
- Точность решения. Точность указываем в количестве точно вычисленных знаков после запятой.
Выделим переменные для этого:
# на старте границы поиска значения логарифма все равны нулю
start = 0
end = 0
middle = 0
# логарифм какого числа мы ищем
num = 600
# основание логарифма
base = 10
# сколько нужно знаков после запятой
accuracy = 4Вычисляем границы
Поиск делаем так: начинаем считать от нуля и на каждом шаге увеличиваем это значение на единицу. Как только мы превысили аргумент (то, от чего берём логарифм) — это наша конечная граница. Соответственно, предыдущее значение, которое на единицу меньше, будет стартовой границей.
# пока основание в очередной степени не превысило само число —
while base**end <= num:
# увеличиваем конечную границу поиска на единицу
end += 1
# откатываемся на один шаг назад от конечной границы, чтобы найти начальную границу
start = end - 1Проверяем, вдруг мы сразу нашли решение
На всякий случай перед тем, как идти дальше, проверим, будет ли решением наша стартовая граница — это сразу может сэкономить нам много сил в дальнейшем:
Проверяем, вдруг мы сразу нашли решение
На всякий случай перед тем, как идти дальше, проверим, будет ли решением наша стартовая граница — это сразу может сэкономить нам много сил в дальнейшем:
# если сразу нашли целое значение степени
if base**start == num:
# выводим решение
print('log(' + str(base) + ')' + str(num) + ' = ' + str(start))
# останавливаем программу
exit(0)Считаем логарифм
Мы будем считать логарифм не классическим способом из высшей математики, а простым приближением — найдём ответ с приемлемой точностью. За точность отвечает переменная accuracy, но в цикле мы её умножим на 4. Это неочевидный ход, поэтому сейчас объясним, в чём тут дело.
На каждом шаге цикла мы делим границу пополам, но если деление выпадает на чётную значимую цифру, то при делении у нас не увеличится количество знаков после запятой. Например, если нам нужна точность 2 знака после запятой, то если вторым шагом цикла мы разделим 0,4 на 2, то у нас останется один знак после запятой (0,2). Таких делений может быть 4 подряд, прежде чем мы доберёмся до следующего знака: 8 → 4 → 2 → 1, поэтому мы и умножаем требуемую точность на 4 — чтобы гарантированно получить нужную точность.
Теперь запишем этот цикл на языке программирования. Его можно было сделать изящнее, например, вложив условные операторы друг в друга или используя оператор множественного выбора, но так получается нагляднее:
# организуем цикл, чтобы получить нужную точность после запятой
for i in range(accuracy*4):
# увеличиваем счётчик цикла
i += 1
# находим серединное значение
middle = (start + end) / 2
# если основание в этой степени больше нашего числа, то сдвигаем к середине конечную границу
if base**middle > num:
end = middle
# если основание в этой степени больше нашего числа, то сдвигаем к середине начальную границу
if base**middle < num:
start = middle
# если основание в этой степени равно нашему числу
if base**middle == num:
# выводим ответ и выходим из цикла
print('log(' + base + ')' + num + ' = ' + start)
breakВыводим ответ
Это самая простая часть алгоритма:
# когда цикл закончился — выводим ответ
print('log(' + str(base) + ')' + str(num) + ' = ' + str(middle))Проверяем работу
Для проверки посчитаем log(10) 600 с помощью нашей программы:
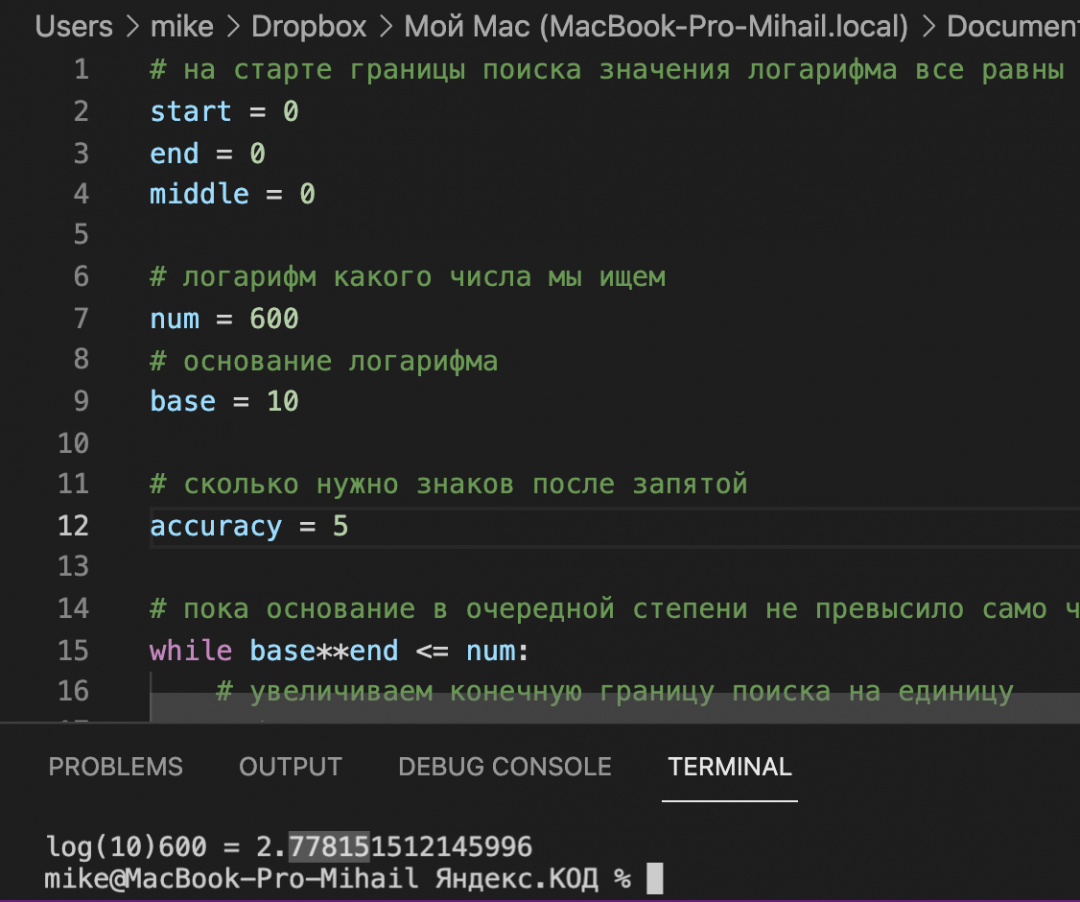
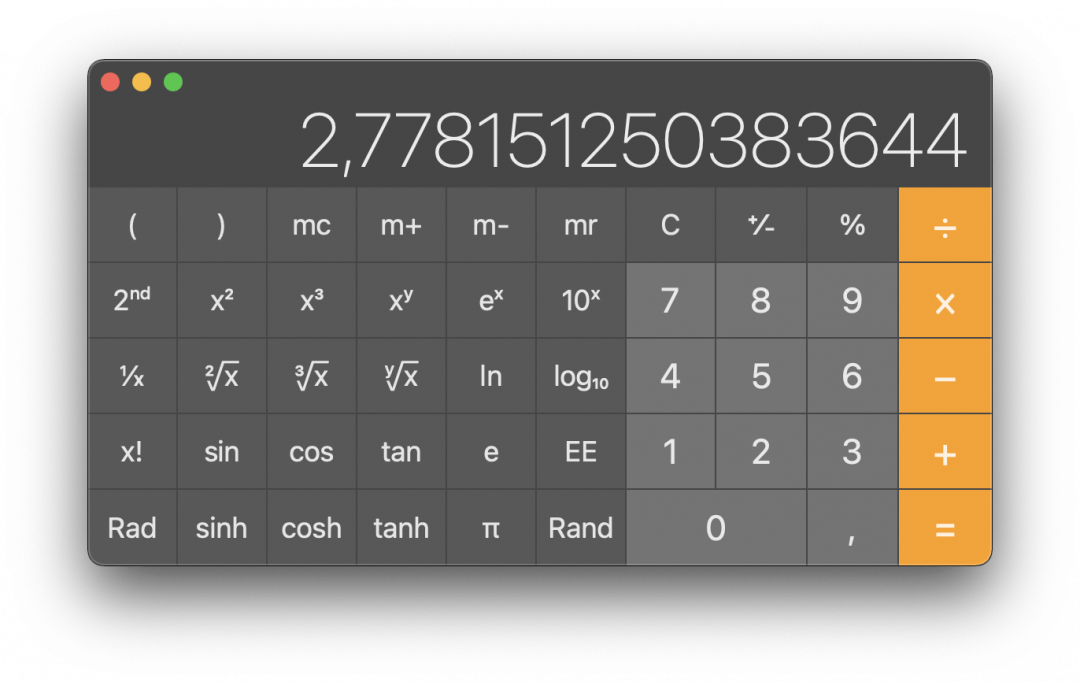
Теперь запустим калькулятор и проверим наше решение:
# на старте границы поиска значения логарифма все равны нулю
start = 0
end = 0
middle = 0
# логарифм какого числа мы ищем
num = 600
# основание логарифма
base = 10
# сколько нужно знаков после запятой
accuracy = 5
# пока основание в очередной степени не превысило само число —
while base**end <= num:
# увеличиваем конечную границу поиска на единицу
end += 1
# откатываемся на один шаг назад от конечной границы, чтобы найти начальную границу
start = end - 1
# если сразу нашли целое значение степени
if base**start == num:
# выводим решение
print('log(' + str(base) + ')' + str(num) + ' = ' + str(start))
# останавливаем программу
exit(0)
# организуем цикл, чтобы получить нужную точность после запятой
for i in range(accuracy*4):
# увеличиваем счётчик цикла
i += 1
# находим серединное значение
middle = (start + end) / 2
# если основание в этой степени больше нашего числа, то сдвигаем к середине конечную границу
if base**middle > num:
end = middle
# если основание в этой степени больше нашего числа, то сдвигаем к середине начальную границу
if base**middle < num:
start = middle
# если основание в этой степени равно нашему числу
if base**middle == num:
# выводим ответ и выходим из цикла
print('log(' + base + ')' + num + ' = ' + start)
break
# когда цикл закончился — выводим ответ
print('log(' + str(base) + ')' + str(num) + ' = ' + str(middle))