Как компьютер считает синусы

Это текст про математику и компьютеры. Если тема интересна, посмотрите также на математический тренажёр Практикума — он бесплатный и интерактивный. 

А сейчас — про синусы.

Что такое синус и зачем он нужен? 

Вульгарное объяснение: синус — это математическая коробка, в которую засовывают любое число, а она в ответ выдаёт числа от −1 до 1. Если эти числа выстроить подряд на некой оси, то получится кривая вот такого вида:

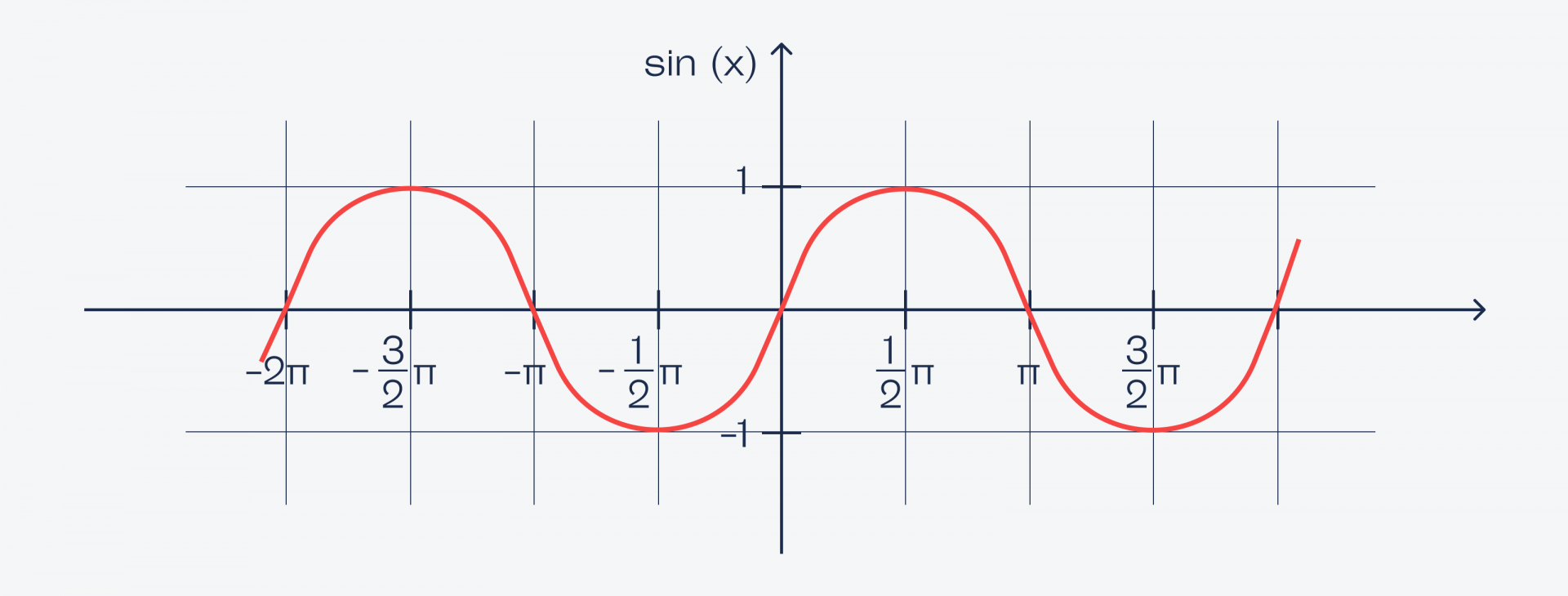
Как читать эту кривую: если затолкать в коробку «sin» число, примерно равное 1,57, то коробка выдаст число, близкое к единице. Если затолкать число 2, на выходе будет примерно 0,909. Если затолкать примерно 3,14 — вернёт примерно 0. Синус от 4,712 даст примерно −0,999. И так дальше: число может быть сколько угодно большим, а синус всегда будет возвращать какие-то дробные значения от −1 до 1.

Это число взято из тригонометрии — то есть из науки, которая занимается углами и сторонами треугольника. В частности, синус описывает отношение сторон прямоугольного треугольника: насколько один из катетов (короткая сторона треугольника) короче, чем гипотенуза (длинная сторона треугольника). Но чаще всего мы знаем не длины сторон, а угол между ними, поэтому в синусы всегда запихивают значения углов.

Грубо говоря, вы говорите коробке: «Коробка, у меня тут прямоугольный треугольник. Я смотрю на его острый угол, он равен 30º. Что ты мне на это скажешь»? А коробка отвечает: «Если у тебя угол 30º, то короткая сторона твоего треугольника вдвое короче, чем длинная гипотенуза. Так что sin(30º) = ½». 

Это число нужно много где в математике и компьютерах. Например, без синуса невозможно соединить две точки прямой линией на плоскости. Люди это делают без труда с помощью линейки, а компьютеру нужно очень чётко считать, куда поставить пиксель, и для этого нужен синус.

Помимо синуса есть ещё три аналогичные функции — косинус, тангенс и котангенс. Они такие же по принципу работы, но описывают отношения других сторон.

Во многих языках программирования есть встроенная команда нахождения синуса угла — sin(). Внутри этой функции зашита какая-то логика для нахождения этого числа. 

Чаще всего, когда не нужна высокая точность, компьютер берёт значения синуса из готовых таблиц — он находит там нужный угол и возвращает значение, ничего не вычисляя. Это быстро и достаточно точно для бытовых вычислений. Вы наверняка использовали его в школе, когда считали синусы по таблице Брадиса. 

Но когда нужна высокая точность вычислений (например, 20 знаков после запятой), то синусы и другие тригонометрические функции высчитывают каждый раз с нуля. Для этого используют много разных алгоритмов, и самый простой из них — использование рядов Тейлора.

Что такое ряд Тейлора

Брук Тейлор — это английский математик из 17-го века, в честь которого назвали формулу, связывающую значение функции и значение всех её производных в выбранной точке. Если сильно упростить и перевести на понятный язык, то формула будет звучать так:

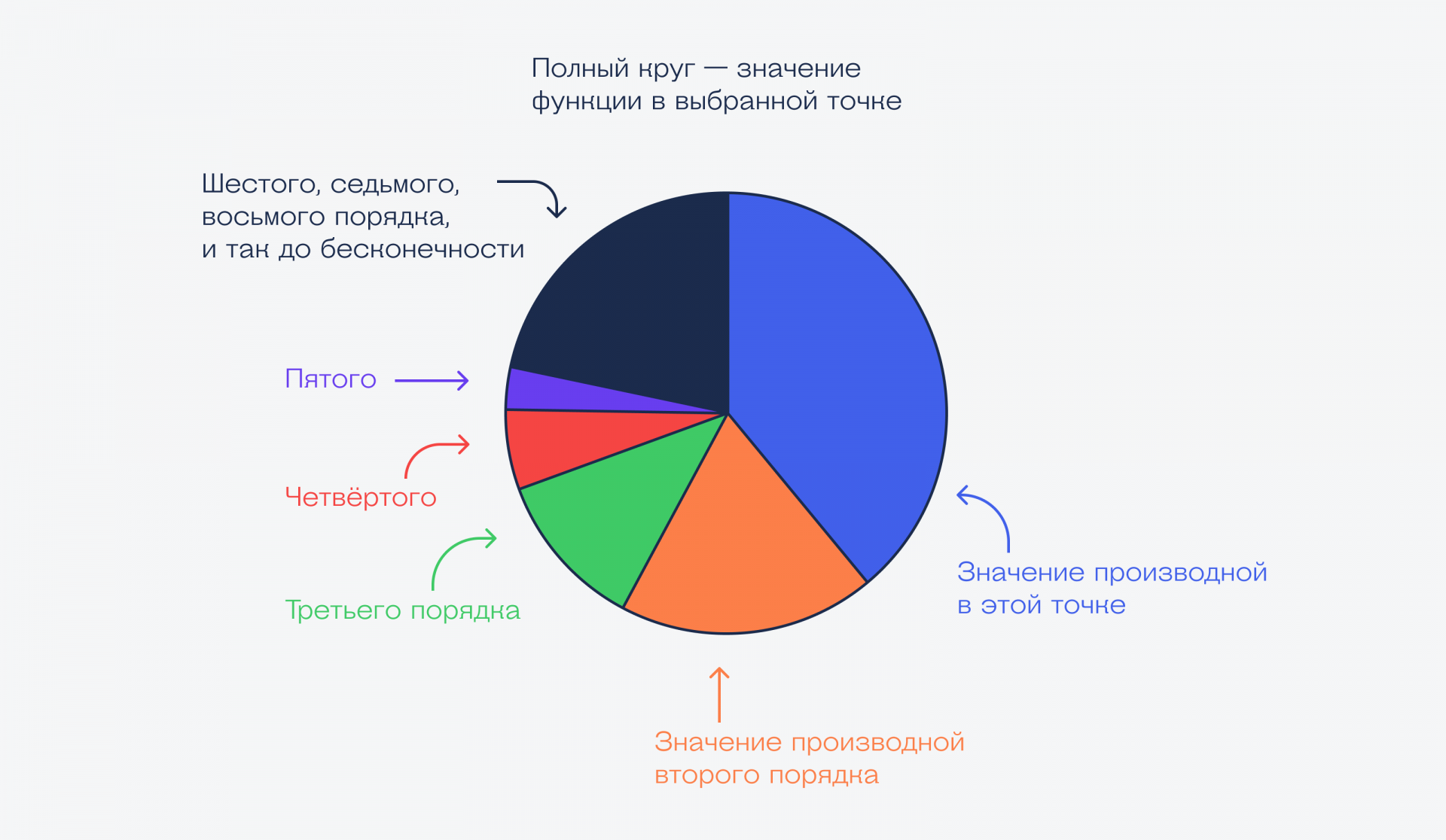
Представим, что значение функции, например, синуса — это круг, заполненный на 100%. Производная функции в этой точке — это часть круга:

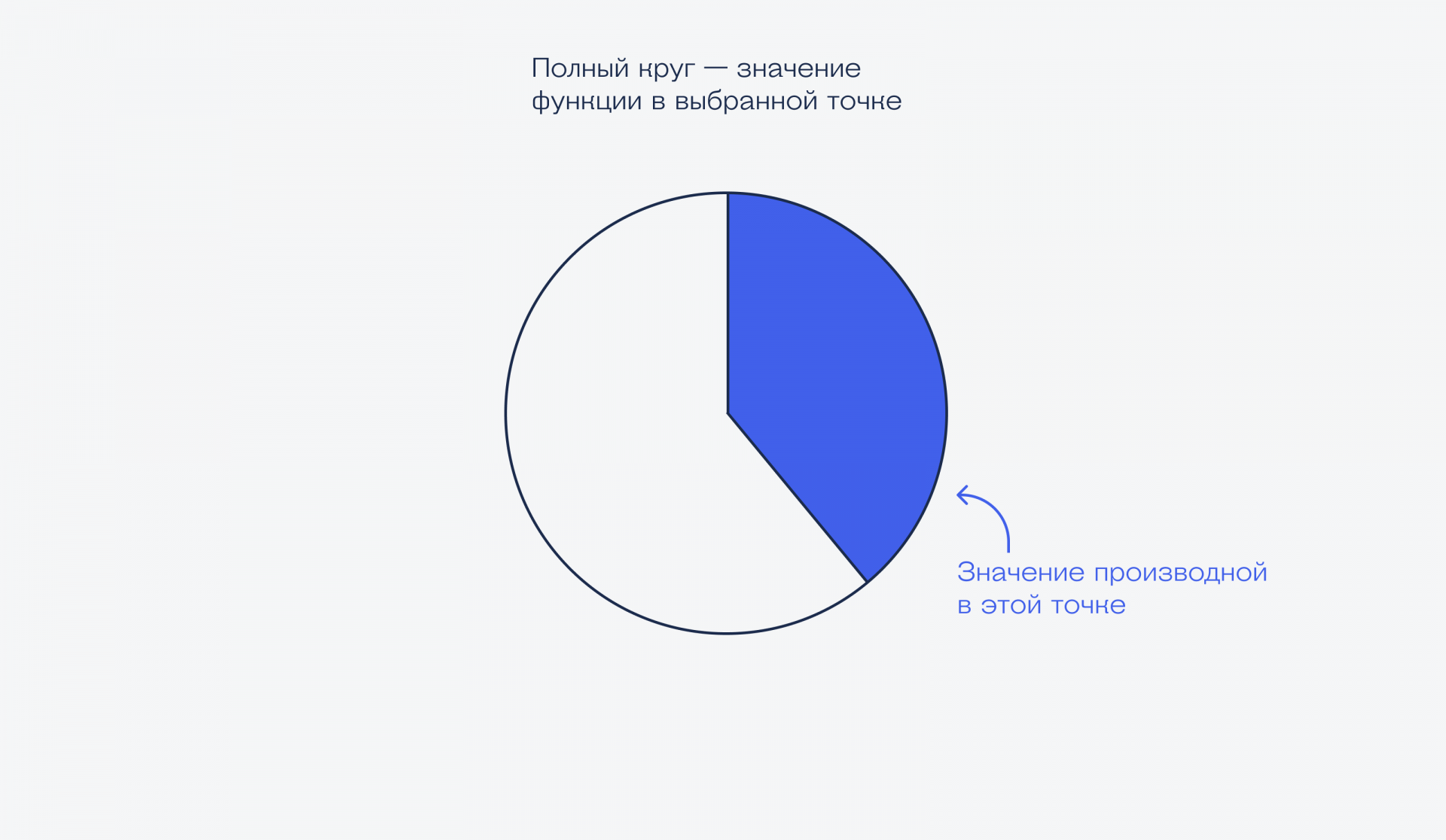
Есть производные первого порядка в этой точке, второго, третьего и так до бесконечности. Каждая производная следующего порядка добавляет в круг сектор поменьше:

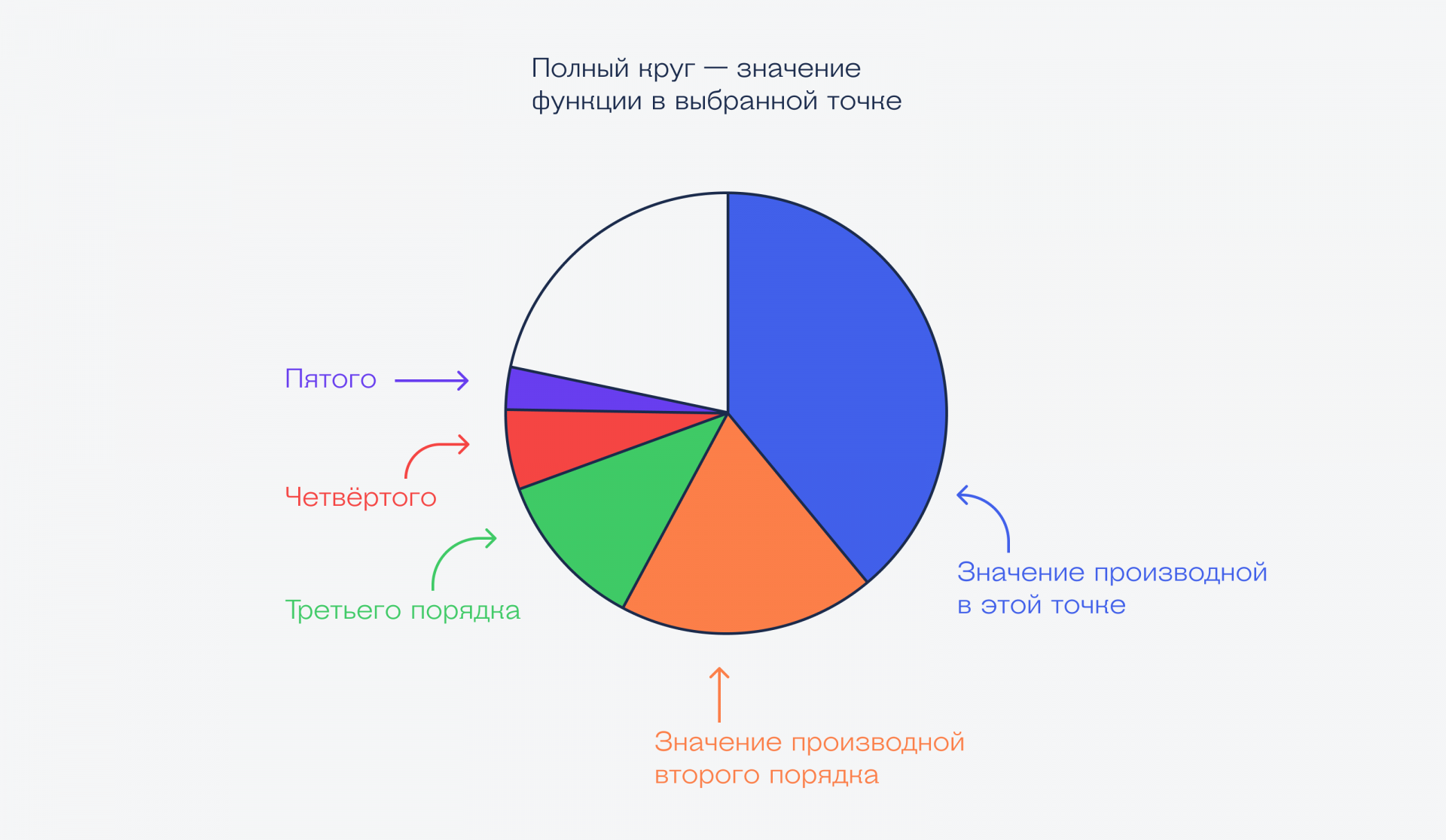
Если сложить все производные до бесконечности, то получим полный круг — это и будет значение синуса:

В общем виде ряд Тейлора функции выглядит так:

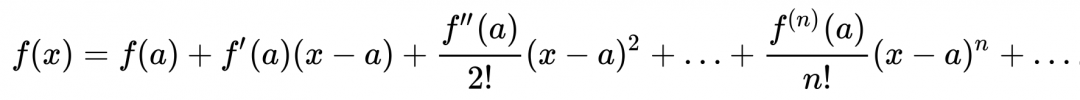
Для каждой функции ряд Тейлора выглядит по-своему. Для синуса он выглядит так:

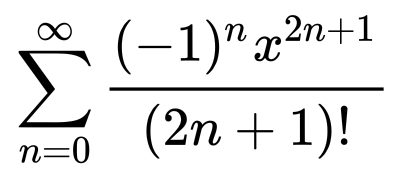
Выглядит сложно. Но если разложить эту формулу сумму в понятный вид, она будет выглядеть так:

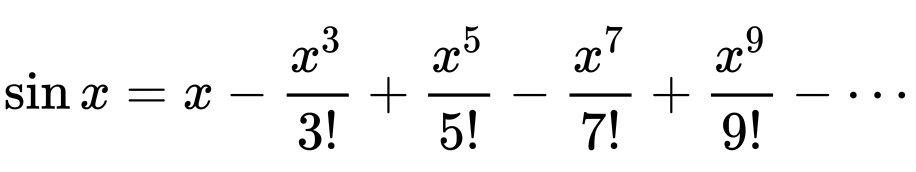
Восклицательный знак — это факториал. Это просто произведение всех целых чисел до этого числа. Например: 5! = 1 × 2 × 3 × 4 × 5 = 120.

Получается, что компьютеру для нахождения синуса достаточно использовать умножение — и для факториала, и для возведения в степень. Зная это, можно написать простой алгоритм.

Точность расчётов

Особенность ряда Тейлора в том, что это бесконечный ряд — а значит, и вычисления тоже придётся делать бесконечно. Чтобы обойти это ограничение, используют погрешность — с какой точностью нам нужно посчитать значение формулы. Для этого делают так:

С таким подходом можно найти синус любого угла с любой точностью, главное, чтобы у компьютера хватило памяти на все эти вычисления.

Радианы

Чтобы использовать ряд Тейлора для вычисления синуса, нам нужно перевести градусы в радианы. Радиан — это мера измерения углов в тригонометрии, которая привязана к числу π. 

Радианы с углами связаны так:

1 радиан = 180/π градусов

Получается, что для того, чтобы перевести углы в градусах в радианы, нам нужно градусы разделить на 180 и умножить на π. 

Теперь мы знаем всё, чтобы написать код вычисления синуса на Python

Пишем код

Логика алгоритма будет такая:

Читайте комментарии, чтобы разобраться в коде, а потом запустите его у себя, чтобы проверить результаты:

# импортируем математическую библиотеку, чтобы взять оттуда модуль и число пи
import math

# объявляем свою функцию, которая посчитает синус
def computerSinus (x,n):
 
    # переводим градусы в радианы
    x = x/180*math.pi
    # для проверки выведем результат, который посчитает компьютер
    print(str(math.sin(x)) + " — результат вычислений встроенного синуса")
    
    # сразу берём x как первое слагаемое ряда Тейлора
    q = x
    # сумма ряда на старте равна нулю
    s = 0
    # порядковый номер слагаемого в ряду Тейлора
    i = 1

    # пока очередное слагаемое больше погрешности — цикл работает
    while abs(q) > n:
        # добавляем слагаемое к общей сумме
        s = s + q
        # вычисляем следующее слагаемое
        q = q* (-1) * (x*x) / ((2*i+1) * (2*i))
        # увеличиваем порядковый номер слагаемого в ряду Тейлора
        i = i+1  
    # возвращаем сумму как результат работы функции
    return s
 
# запрашиваем стартовые значения
x = float(input("Введите градусы: "))
n = float(input("Введите погрешность: "))
# выводим результат, который мы посчитали сами
print(str(computerSinus(x,n)) + " — синус, который мы посчитали")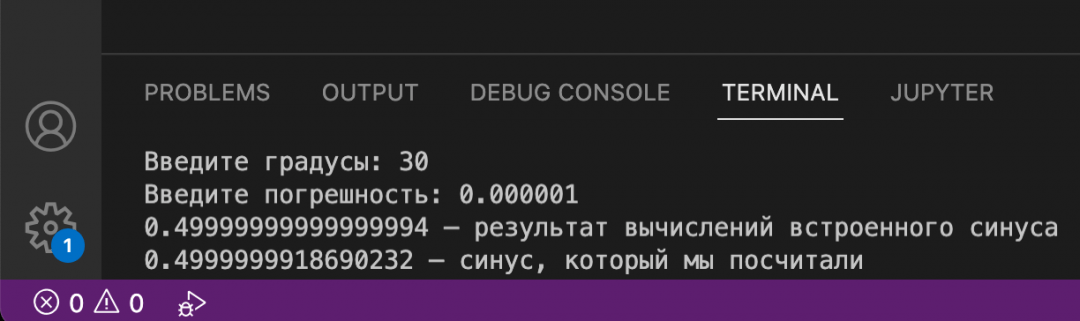

Что дальше

В следующий раз попробуем сделать то же самое с квадратным корнем — посмотрим, как компьютер сможет посчитать его без таблиц.

Любите математику? Это для вас

Попробуйте бесплатный тренажер «Основы математики для цифровых профессий». Это все необходимые знания, чтобы закрыть пробелы в математике для айтишника.

Попробовать бесплатно