Программист развлекает сына:
— Загадай любое целое число от 0 до 100!
— Загадал.
— Спорим, я угадаю его за 7 попыток или быстрее? Я буду называть числа, а ты — отвечать, оно больше, меньше или равно загаданному.
— Ахахах, ты не сможешь угадать за 7 попыток!
— Спорим, угадаю!
— Ну давай, покажи своё кунфу…
6 попыток спустя отец угадал число, а ребёнок сидит в шоке. Они попробовали снова, и во второй раз отец угадал число за семь попыток. В третий — за четыре. Сколько бы они ни играли, число всегда угадывалось за 7 попыток или менее.
Вопрос: как?
Это простейшая алгоритмическая задача, которую показывают на первом уроке информатики, чтобы показать мощь алгоритмического мышления. Смысл в том, чтобы...
👉 каждый раз называть число, которое делит пополам диапазон возможных чисел.
Этот приём каждый раз в 2 раза сокращает область поиска, и в конце нам становится легко угадать даже простым перебором.
Допустим, сын загадал число 63. Тогда делаем так:
- Находим середину диапазона от 0 до 100 — это 50. Называем это число. Сын говорит «Больше».
- Значит, его число лежит в диапазоне от 50 до 100. Находим его середину — 75. Называем это число. Сын говорит «Меньше».
- Ага, значит, его число находится в диапазоне от 50 до 75. Находим середину — 62. Называем это число. Сын говорит «Больше».
- Поиск снова сузился: от 62 до 75. Середина — 67. Называем это число. Сын говорит «Меньше».
- У нас осталось 3 попытки и 4 числа. Найдём ещё одну середину — 64. Называем это число. Сын говорит «Меньше».
- Раз у нас число, которое больше, чем 62, и меньше, чем 64, то это число 63. Даже седьмая попытка не понадобилась.
Этим способом можно угадать любое число от 0 до 100 за 7 попыток или меньше. Главное — быстро и правильно считать в уме середину и помнить, как выглядит сейчас твой рабочий диапазон.
А если число будет больше?
На самом деле за 7 шагов можно угадать любое число от 0 до 127 или от 1 до 128. Всё потому, что два в седьмой степени — это как раз 128. Каждый раз, когда мы делим рабочий диапазон на 2, мы как будто убираем одну степень у двойки, постепенно уменьшая наш диапазон угадывания до двух чисел. Для верности лучше добавить ещё попытку.
Если бы у нас было 8 попыток, можно было бы угадывать числа до 256. 9 попыток — 512 и так далее.
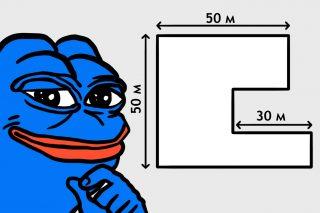Задача про охрану периметра
Решаем как программисты: таракан на стене
Решаем кодом задачу про безумного рекрутера
Решаем кодом задачу про наноботов
Решаем кодом: программа угадает число за 7 попыток
Простейший математический фокус
Как вычислить день рождения
Мама против вирусов
Задача про периметр и забывчивого монтажникаА где это используется в народном хозяйстве?
На этом принципе построена модель данных «Бинарное дерево» — это одна из важнейших технологий для составления словарей и поиска данных. Прочитайте об этом в статье про бинарные деревья.
