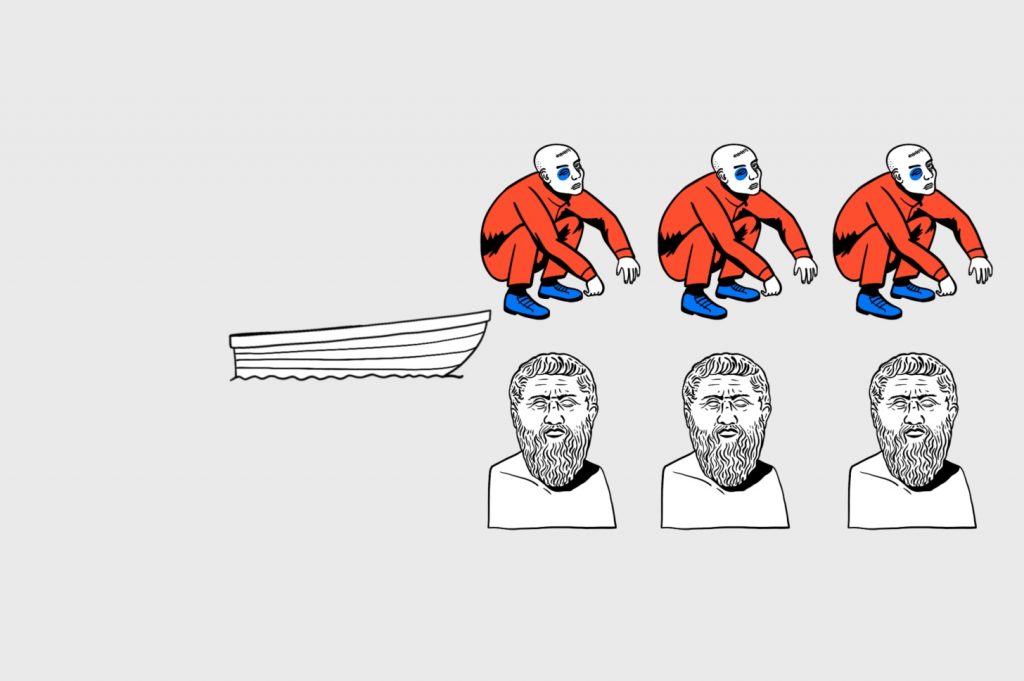
Это кавер-версия задачи про волка, козу и капусту — классическую задачу на алгоритмическое мышление. Она очень простая для разработчиков, и если вы можете решить её с первого раза, можете гордиться собой — только 1 человек из 10 решает эту задачу правильно с первого раза.
Зачем уметь решать такие задачи: помогает в составлении сортировочных алгоритмов и успешно проходить собеседования в ИТ-компаниях. Также важно уметь обосновывать свой ход мыслей.
Ситуация. На одном берегу реки находятся шесть человек: три гопника и три философа. Пока что они ведут непринужденные беседы об экзистенциальном, но все они должны будут рано или поздно оказаться на другом берегу.
Есть одна лодка, в которую могут поместиться только два человека, но философы управлять лодкой не умеют, а гопники умеют. Также нельзя оставлять на одном берегу философов больше, чем гопников, потому что тогда философы взорвут мозг гопникам разговорами о природе вещей. Как переправить всех через реку?
Для первой поездки есть четыре варианта:
- один гопник — не подходит, потому что на берегу философов становится больше и они взорвут мозг;
- два гопника — не подходит по той же причине;
- один или два философа — тоже нет, потому что они не умеют управлять лодкой;
- философ и гопник — единственный вариант, который остаётся.
Значит, первым рейсом пара «философ-гопник» отправляется на другой берег:
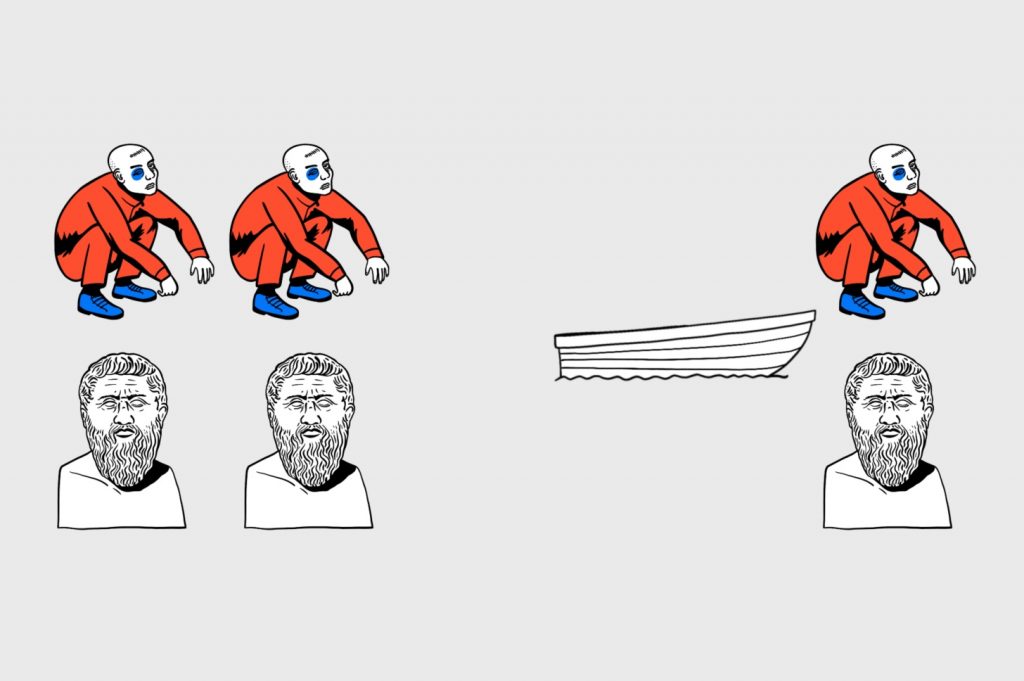
Теперь лодку надо как-то отправить назад. Но так как философ не умеет ей управлять, то он остаётся на берегу, а гопник — возвращается. Философы не взрывают никому мозг:
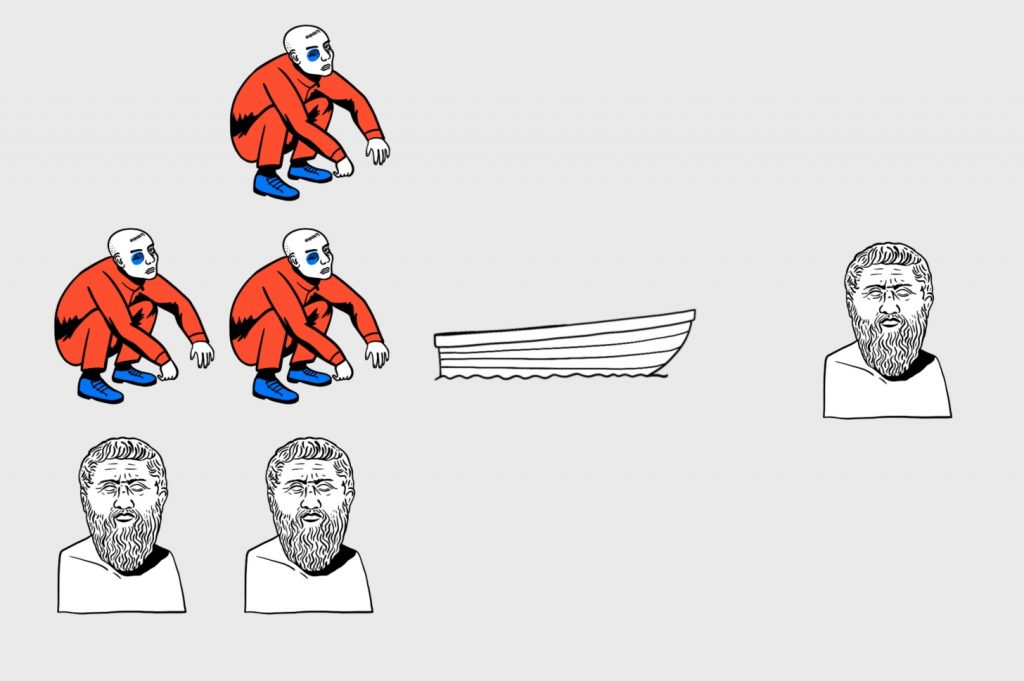
Теперь прикинем варианты следующего рейса. Мы не можем отправить двух гопников, иначе философы останутся в большинстве, и настанет на левом берегу полный экзистенциализм.
Поэтому снова на тот берег уплывают философ с гопником. Причём гопник высаживает философа, но сам из лодки не вылезает — если так не сделать, то он останется с двумя философами на том берегу и они увлекут разговорами об идеях вещей:
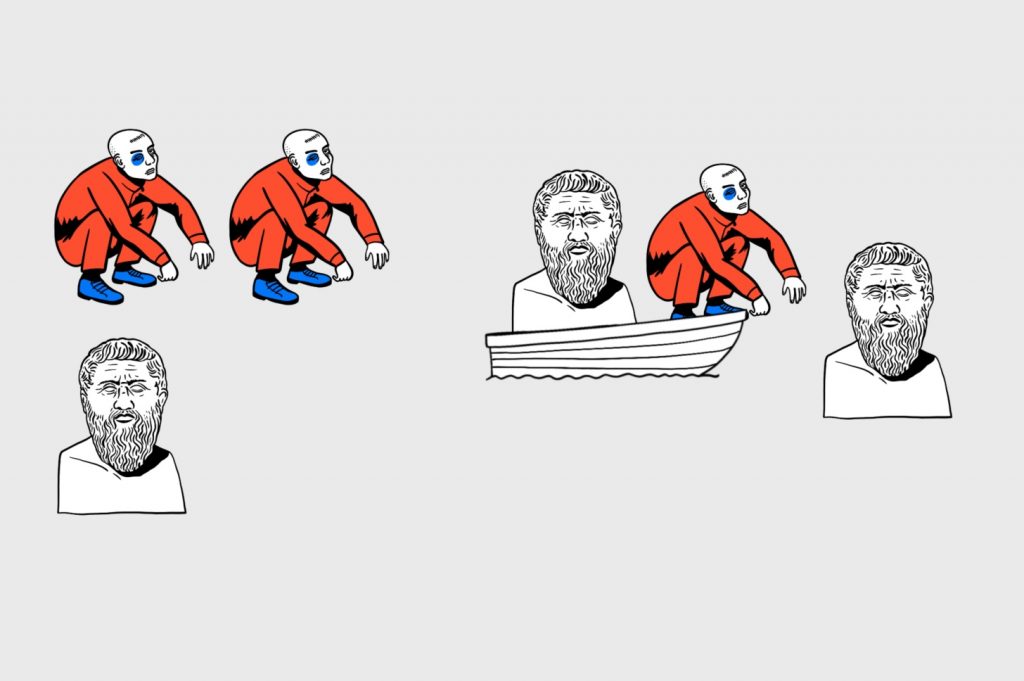
Таким образом, у нас на том берегу сидят два философа, а на этом — один философ и три гопника, на которых он вряд ли сможет воздействовать силой дискурса:
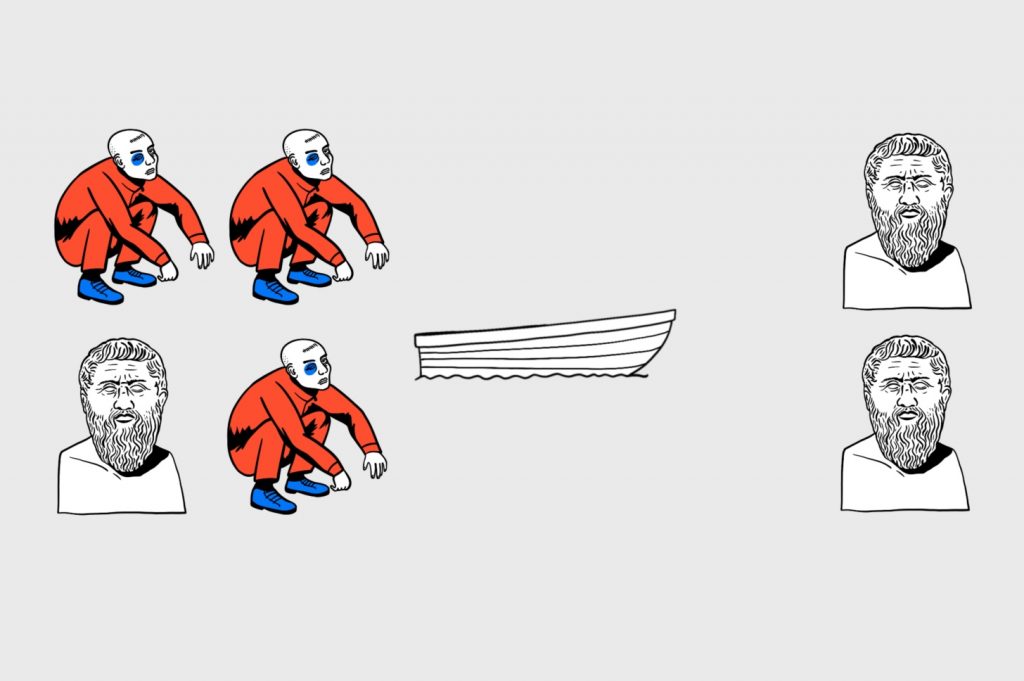
Теперь нам нужно сделать выбор, кто поедет на этот раз. Можно отправить снова философа и гопника, но тогда на том берегу окажутся три философа. И безопасно перевезти остальных гопников поодиночке уже не получится — философы всегда будут в большинстве.
Значит, остаётся только один вариант: отправить в путь двух гопников. В итоге на том берегу всех будет поровну и всё пройдёт спокойно:
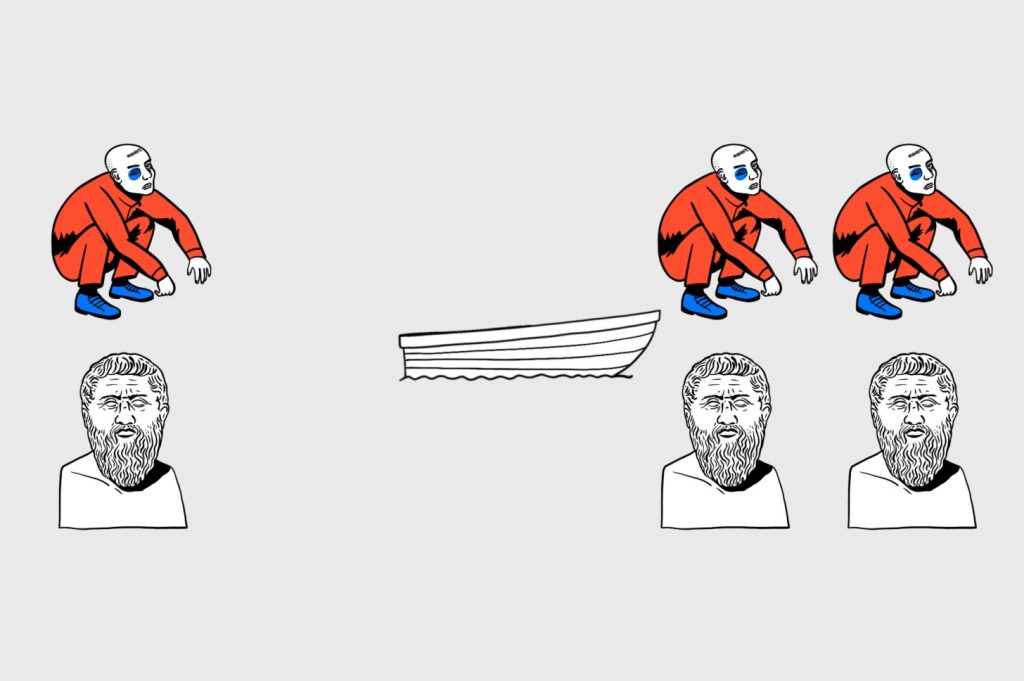
Но лодку надо как-то отправить на другой берег. Нельзя разместить на ней одного гопника, потому что второй останется в меньшинстве среди философов. Двум гопникам ехать обратно тоже не вариант, потому что они только что прибыли.
Поэтому назад отправляются философ и гопник:
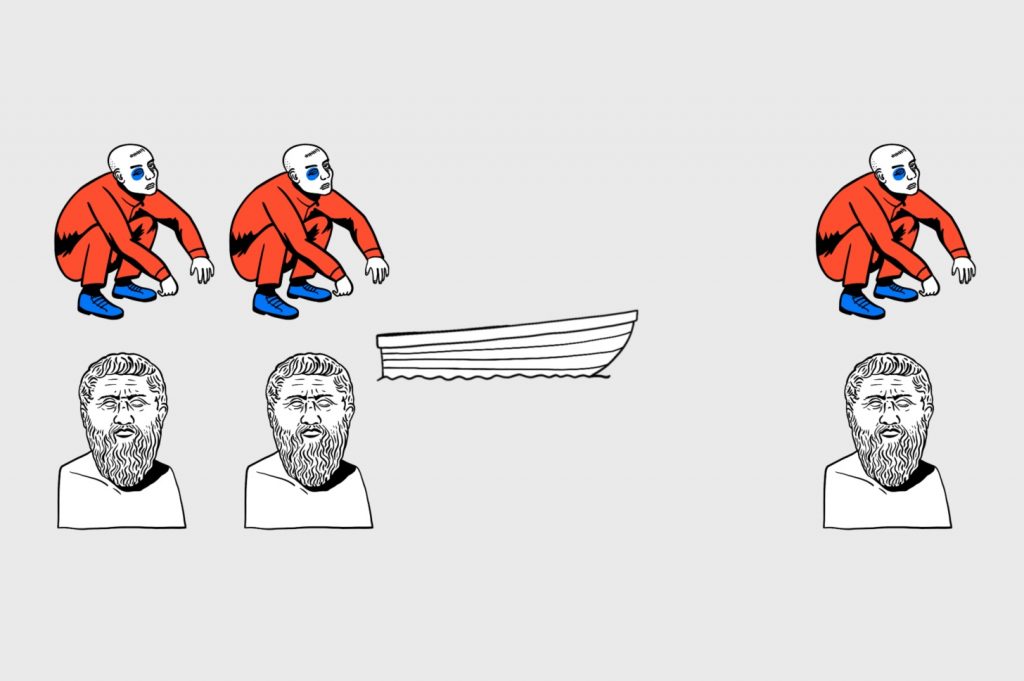
Теперь единственный безопасный вариант — отправить на тот берег двух гопников:
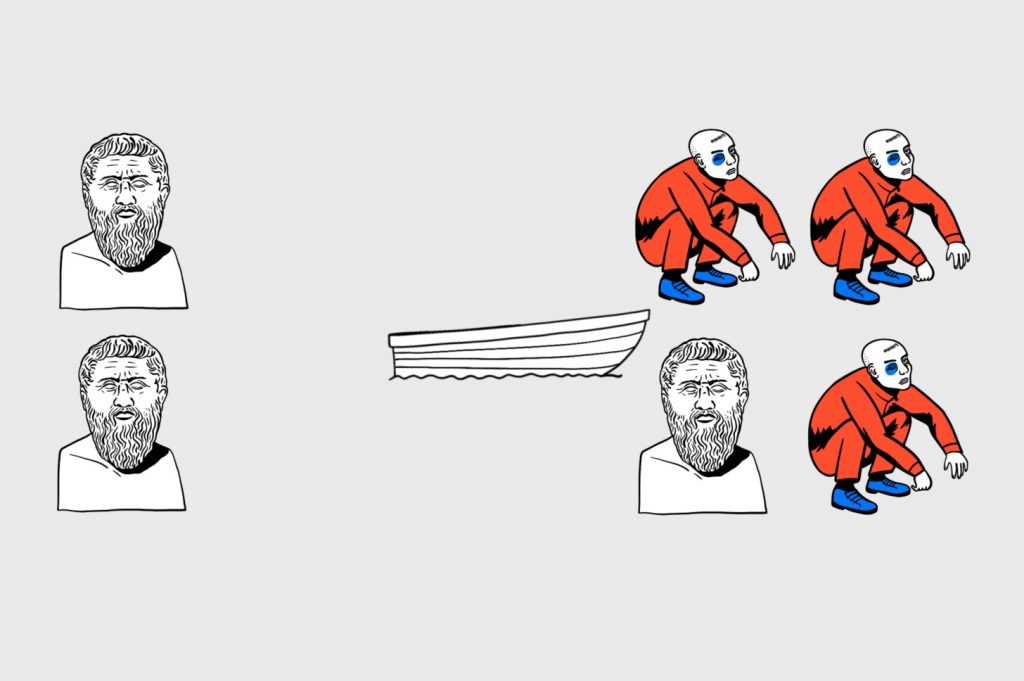
Назад отправим одного гопника. Чтобы не выходить из лодки, он позовёт в неё философа (например, фразой «Что вы думаете о солипсизме?») и вернётся с ним обратно на тот берег:
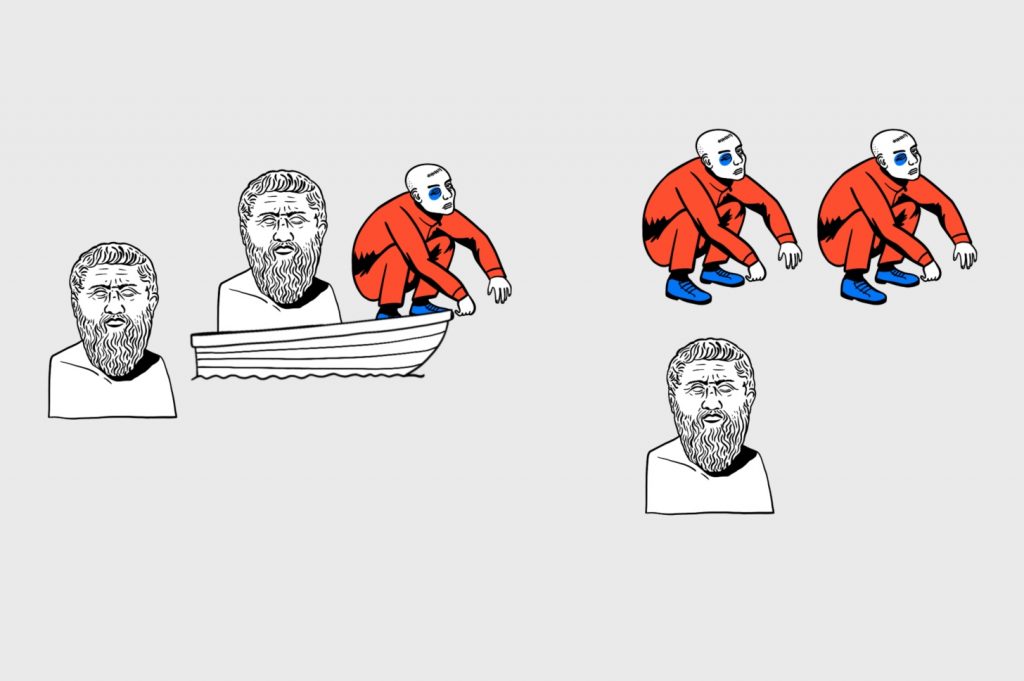
Точно так же забираем оставшегося философа:
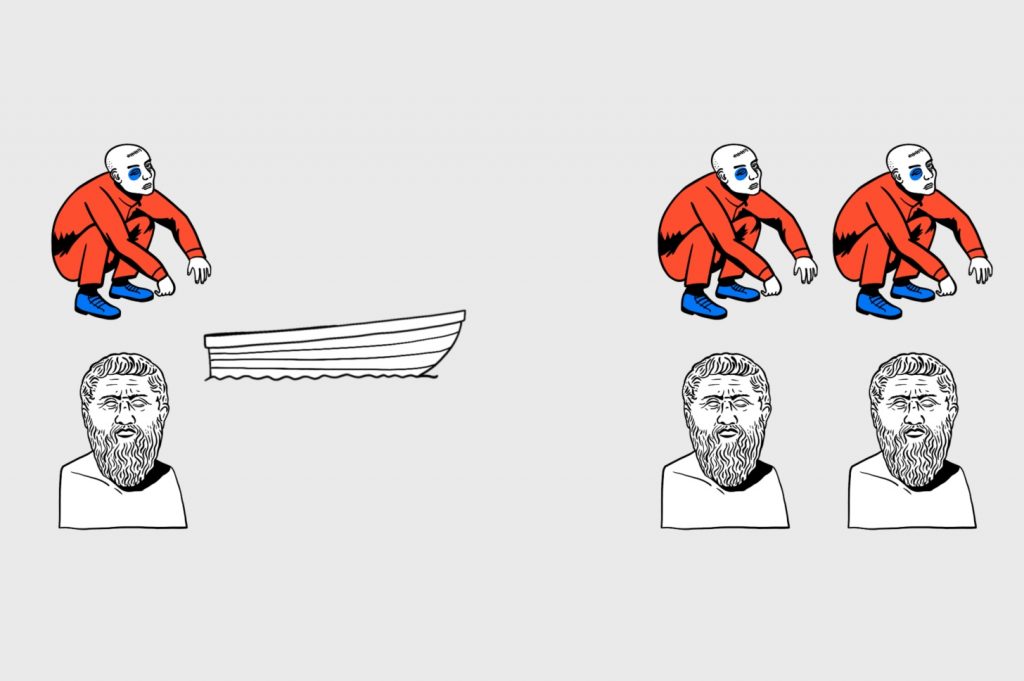
И в итоге вся компания оказывается на том берегу, бездонное небо — над головой, а нравственный закон — внутри: