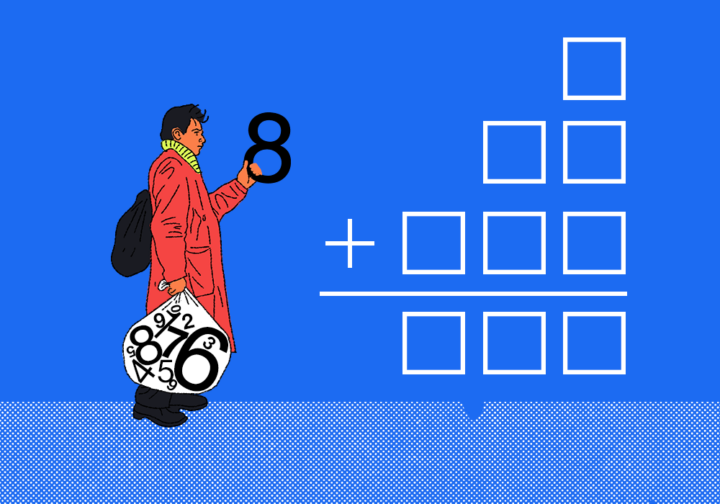
Простая школьная задача: есть числа 6, 6, 2, 2, 8, 8, 0, 0, 0. Из них нужно составить четыре числа: одно-, двух- и трёхзначное, которые в сумме дают четвёртое трёхзначное.
Звучит просто, но с ответом могут быть сложности. Попробуйте решить эту задачку сами, а ответом поделитесь в комментариях.
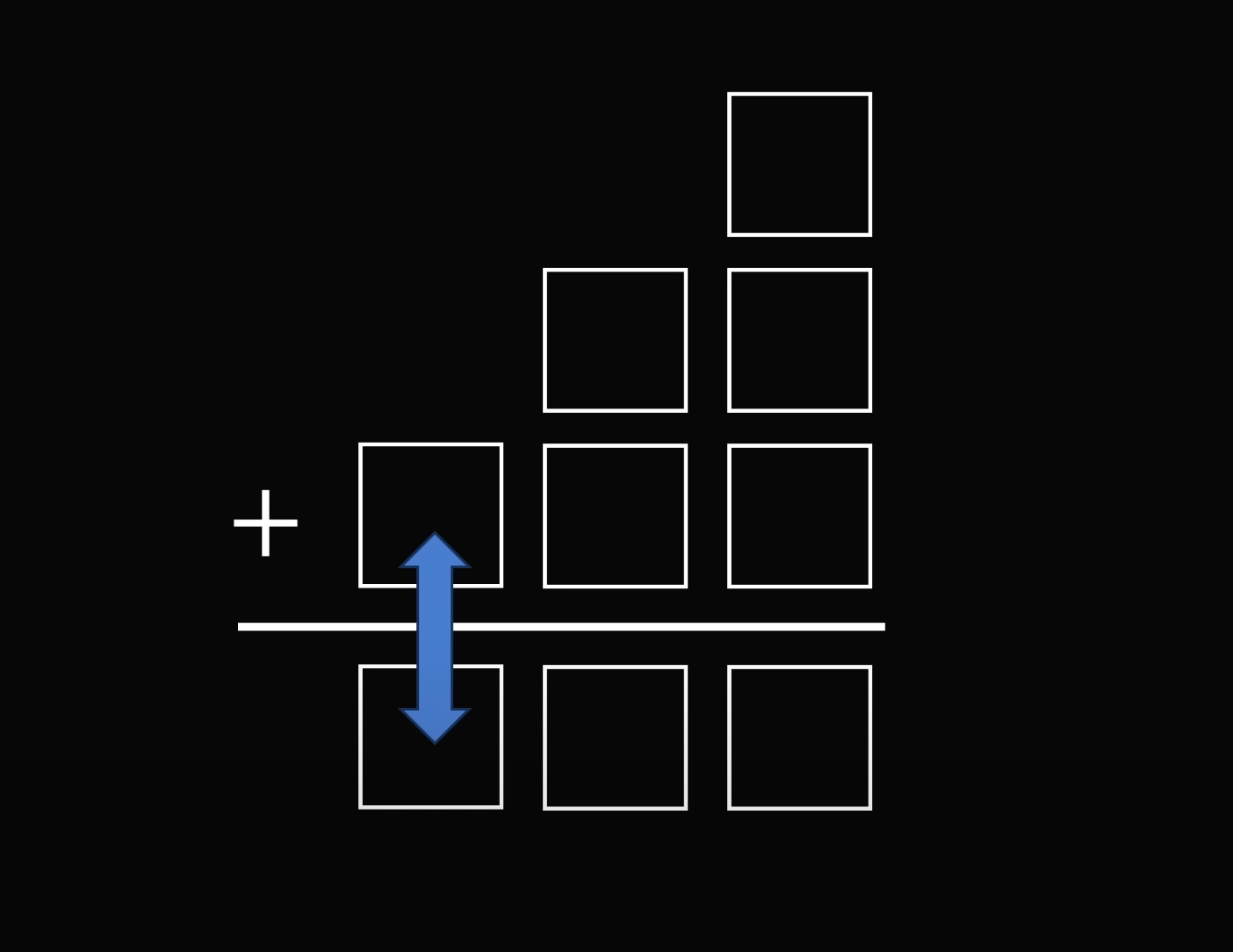
Начнём с того, что представим нашу задачу визуально:

Теперь подберём варианты, при которых сумма чисел над чертой совпадёт с числом под ней. Представим, что трёхзначные числа начинаются с одной и той же цифры:
Попробуем подставить на её место шестёрку:
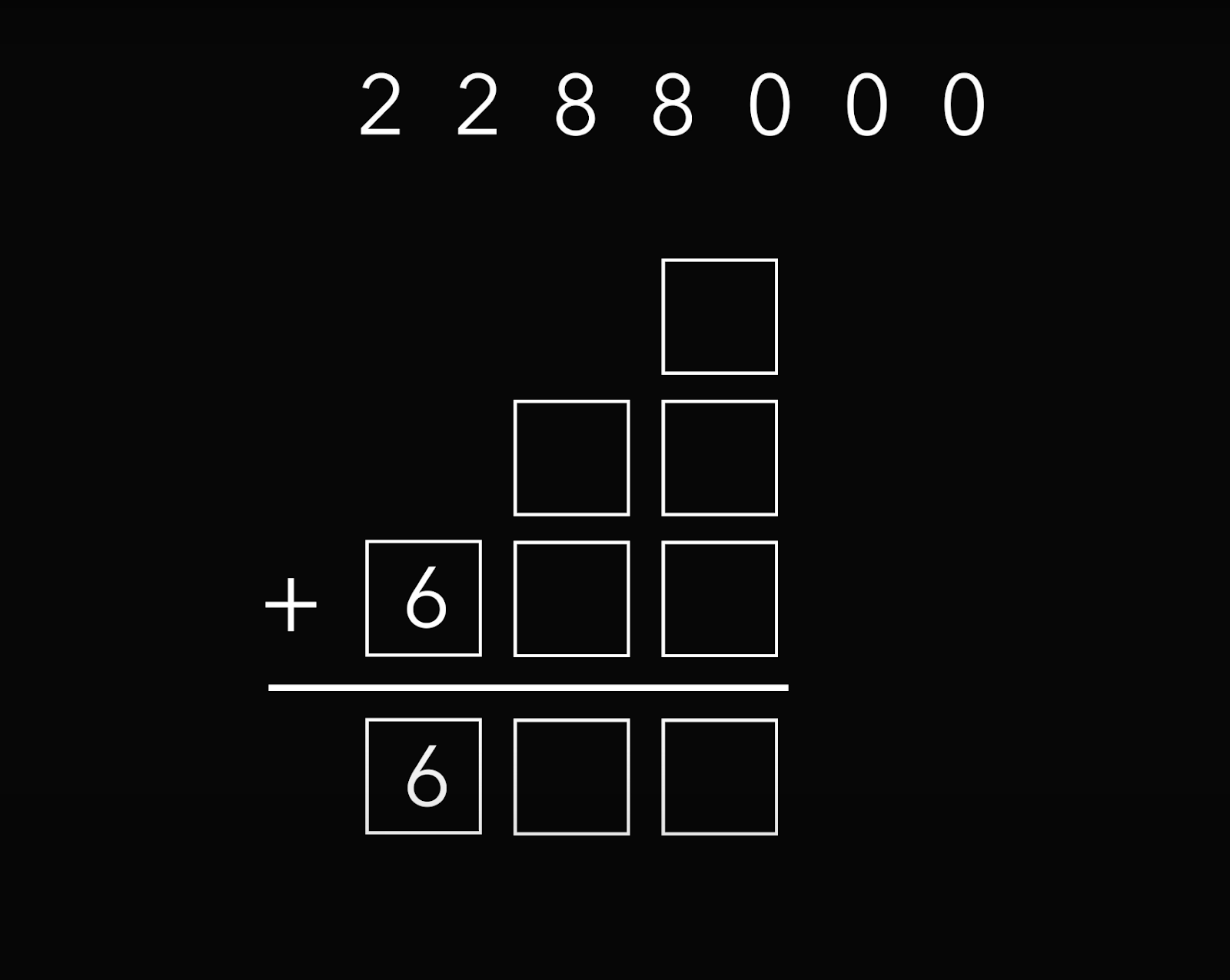
Теперь посмотрим на средний столбик:
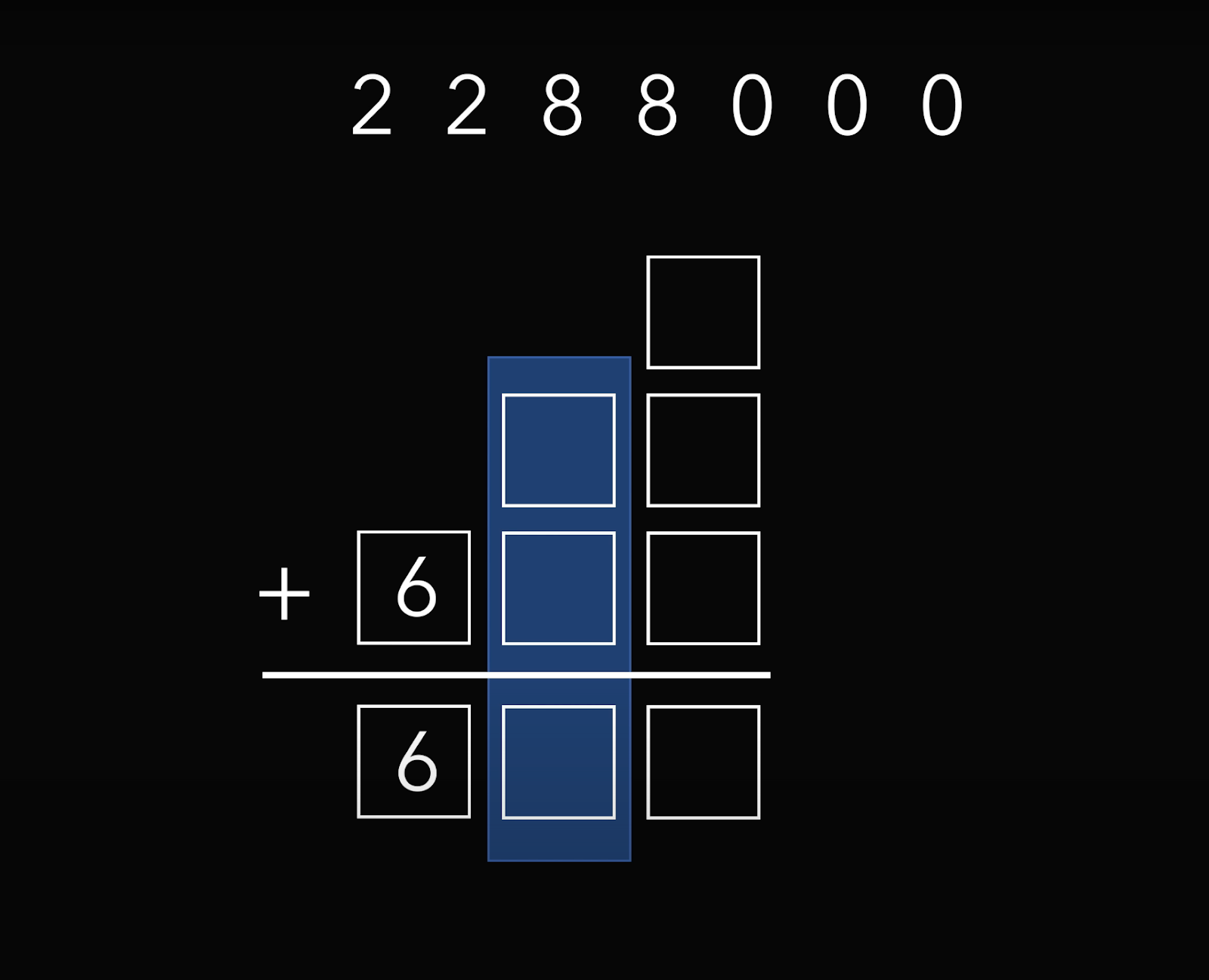
Подставим в них двойку и ноль над чертой и двойку под чертой. Это удовлетворяет нашему условию:
2 + 0 = 2

У нас остались две восьмёрки и два нуля и четыре пустые ячейки:
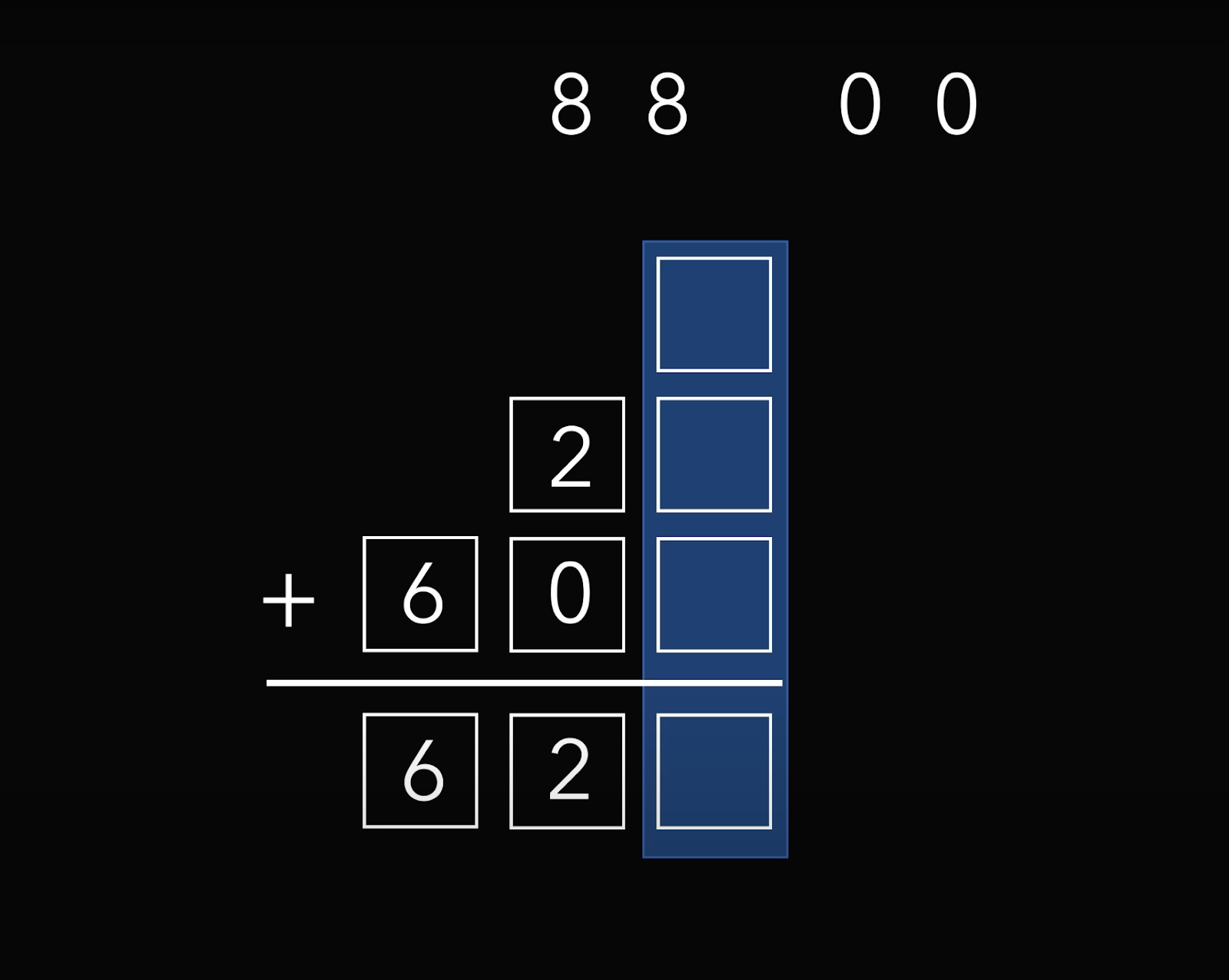
Распределим цифры так, чтобы сумма совпадала:
8 + 0 + 0 = 8
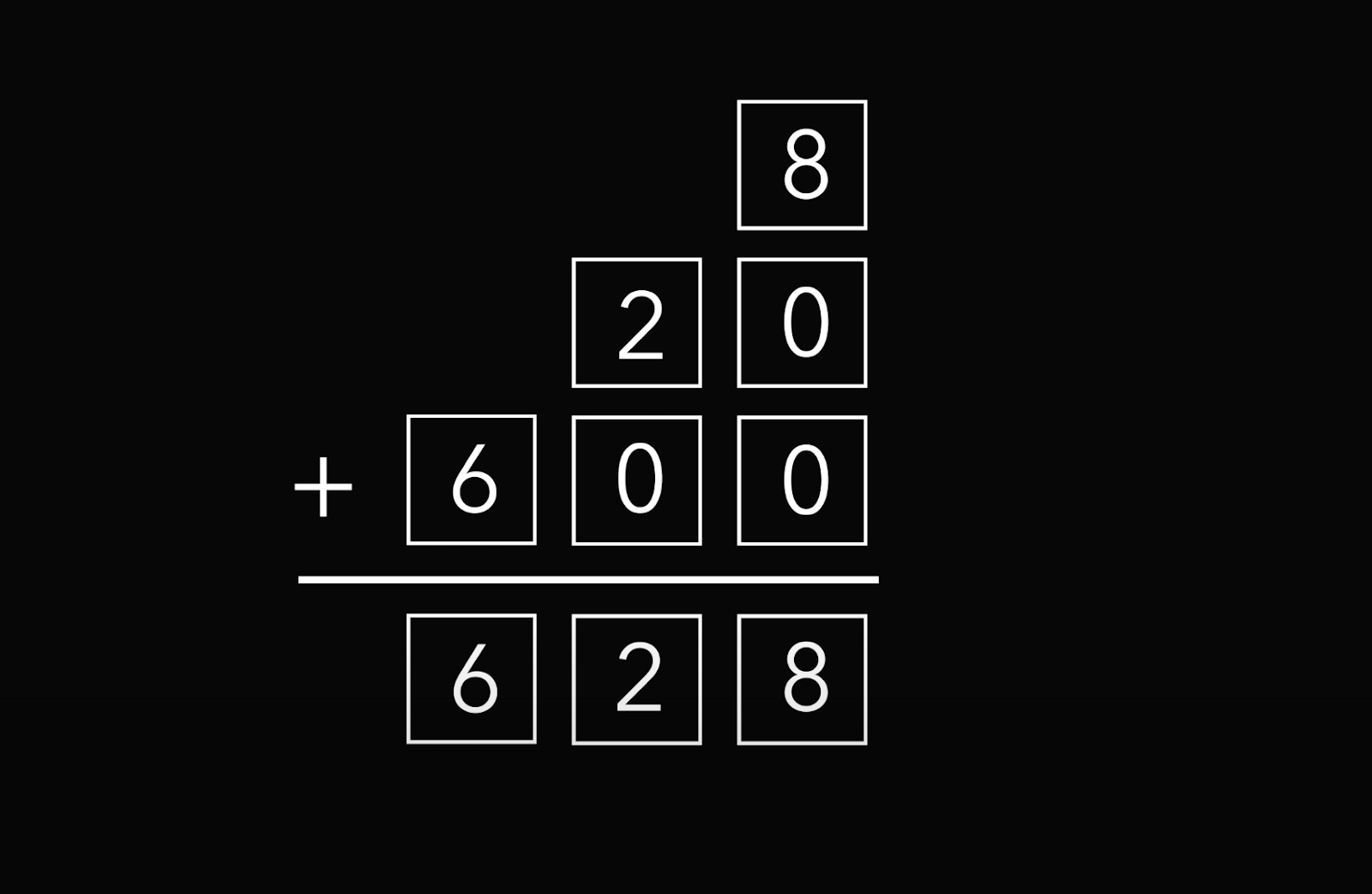
Проверяем, всё сходится:
8+ 20 + 600 = 628
Но это не единственное решение. Если присмотреться и подумать, можно найти ещё комбинации чисел, которые дадут также верную сумму. Попробуйте найти их все, теперь уже самостоятельно (и их не так много, как кажется)
Чтобы не перебирать все варианты чисел вручную, поручим это компьютеру. Для этого поступим так:
- Соберём все доступные числа в один список.
- Найдём все доступные перестановки этого списка. То, что они будут повторяться из-за одинаковых чисел, — ничего страшного, с этим разберёмся позже.
- Теперь будем перебирать все получившиеся перестановки по очереди.
- Первая цифра из очередной перестановки будет означать первое число, вторые две — второе, следующие три — третье и оставшиеся три числа сформируют результат.
- Сложим полученные числа и сравним с результатом. Если одно равно другому — мы нашли решение, выводим его на экран.
- Параллельно с этим посчитаем, сколько всего решений у нас получится.
Теперь о числах. По условию у нас складывается одно-, двух- и трёхзначное число. Можно долго спорить о том, считается ли число с нулём в начале, например, двузначным или трёхзначным, но мы решили так: не считается. Из этого и будем исходить в коде.
Для решения используем Python — в нём уже есть готовая библиотека для получения перестановок.
Как установить Python на компьютер и начать на нём писать
Прежде всего подключаем библиотеку, которая поможет нам с перестановками:
# модуль для быстрого получения всех перестановок
import itertools
Теперь заполняем стартовыми значениями нужные переменные:
# все числа из задачи
numbers = [6,6,2,2,8,8,0,0,0]
# общее количество найденных решений
count = 0
# проверенные комбинации
tested = []
# получаем все перестановки всех чисел
numbers_perm = list(itertools.permutations(numbers))Перед тем как делать цикл, подсветим два момента:
- Перед тем как составить второе и третье число, мы проверяем, первое число там ноль или нет. Если в одной из них ноль — ничего не делаем и сразу переходим к следующей перестановке. Если не ноль — всё в порядке, собираем числа. Число с результатом проверяем точно так же.
- У нас повторяются числа внутри списка, поэтому при перестановке может получиться так, что просто поменяются местами две первые шестёрки. Для компьютера это разные перестановки, для нас — нет. Чтобы избежать повторов в решении, добавим список с проверенными перестановками. Как только нашли очередное решение — заносим эту перестановку в список, а в самом начале цикла будем проверять, есть ли текущая комбинация в этом списке или нет. Если она там есть — переходим сразу к следующей, чтобы не повторяться.
Учитывая всё это, пишем основной цикл:
# перебираем все перестановки по очереди
for i in range(len(numbers_perm)):
# если такую перестановку мы уже проверяли — переходим сразу к следующей итерации цикла
if numbers_perm[i] in tested:
continue
# получаем первое число
first = numbers_perm[i][0]
# если первая цифра второго числа — ноль, то переходим к следующей итерации цикла
if numbers_perm[i][1] == 0:
continue
# получаем второе число
second = 10 * numbers_perm[i][1] + numbers_perm[i][2]
# точно так же собираем третье число
if numbers_perm[i][3] == 0:
continue
third = 100 * numbers_perm[i][3] + 10 * numbers_perm[i][4] + numbers_perm[i][5]
# и собираем результат
if numbers_perm[i][6] == 0:
continue
result = 100 * numbers_perm[i][6] + 10 * numbers_perm[i][7] + numbers_perm[i][8]
# если сумма получается верной
if first + second + third == result:
# выводим найденное решение на экран
print(str(first) + ' + ' + str(second) + ' + ' + str(third) + ' = ' + str(result))
# увеличиваем количество найденных решений на единицу
count = count + 1
# добавляем проверенную комбинацию в список
tested.append(numbers_perm[i])Последнее, что нам осталось сделать, — вывести общее количество найденных решений:
# выводим общее количество найденных решений
print('Всего решений: ' + str(count))
Запустите код, чтобы узнать, сколько же на самом деле решений имеет задача и каких. А потом сравните это с тем, что получилось у вас, когда вы решали эту задачу без кода.
# модуль для быстрого получения всех перестановок
import itertools
# все числа из задачи
numbers = [6,6,2,2,8,8,0,0,0]
# общее количество найденных решений
count = 0
# проверенные комбинации
tested = []
# получаем все перестановки всех чисел
numbers_perm = list(itertools.permutations(numbers))
# перебираем все перестановки по очереди
for i in range(len(numbers_perm)):
# если такую перестановку мы уже проверяли — переходим сразу к следующей итерации цикла
if numbers_perm[i] in tested:
continue
# получаем первое число
first = numbers_perm[i][0]
# если первая цифра второго числа — ноль, то переходим к следующей итерации цикла
if numbers_perm[i][1] == 0:
continue
# получаем второе число
second = 10 * numbers_perm[i][1] + numbers_perm[i][2]
# точно так же собираем третье число
if numbers_perm[i][3] == 0:
continue
third = 100 * numbers_perm[i][3] + 10 * numbers_perm[i][4] + numbers_perm[i][5]
# и собираем результат
if numbers_perm[i][6] == 0:
continue
result = 100 * numbers_perm[i][6] + 10 * numbers_perm[i][7] + numbers_perm[i][8]
# если сумма получается верной
if first + second + third == result:
# выводим найденное решение на экран
print(str(first) + ' + ' + str(second) + ' + ' + str(third) + ' = ' + str(result))
# увеличиваем количество найденных решений на единицу
count = count + 1
# добавляем проверенную комбинацию в список
tested.append(numbers_perm[i])
# выводим общее количество найденных решений
print('Всего решений: ' + str(count))