Два альпиниста-программиста решили установить радиоканал для передачи данных с двух сторон горы. Когда они посмотрели записи, сделанные другими альпинистами, то увидели, что гора начинается под углом 45 градусов, вершины и впадины образуют прямые углы, а в самом конце есть отвесная скала высотой 10 километров.
Посмотрев на схему, альпинист поопытнее сказал, что связь установить не получится, потому что по прямой будет больше 25 километров, а это предел для передатчика. На это второй ответил, что связь точно будет. Кто из них прав?
 Коктейльная задача про доли и крепость
Коктейльная задача про доли и крепость Задача про программистов и угощение в баре
Задача про программистов и угощение в баре Задача про тренера и каратиста
Задача про тренера и каратиста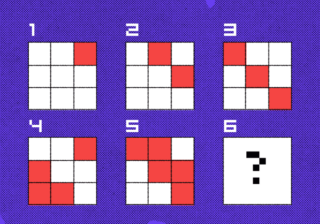 Задача про шаблонное мышление
Задача про шаблонное мышление Сборник задач на логику для тренировки мозга
Сборник задач на логику для тренировки мозга Лучшие задачи, где потребуется нестандартное мышление
Лучшие задачи, где потребуется нестандартное мышление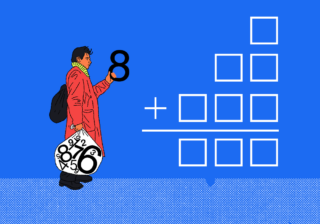 Простая школьная задача про числа, с которой иногда не могут справиться взрослые
Простая школьная задача про числа, с которой иногда не могут справиться взрослые(Мы знаем, что таких высоких гор нет, но всё же попробуйте определить победителя в этом споре)
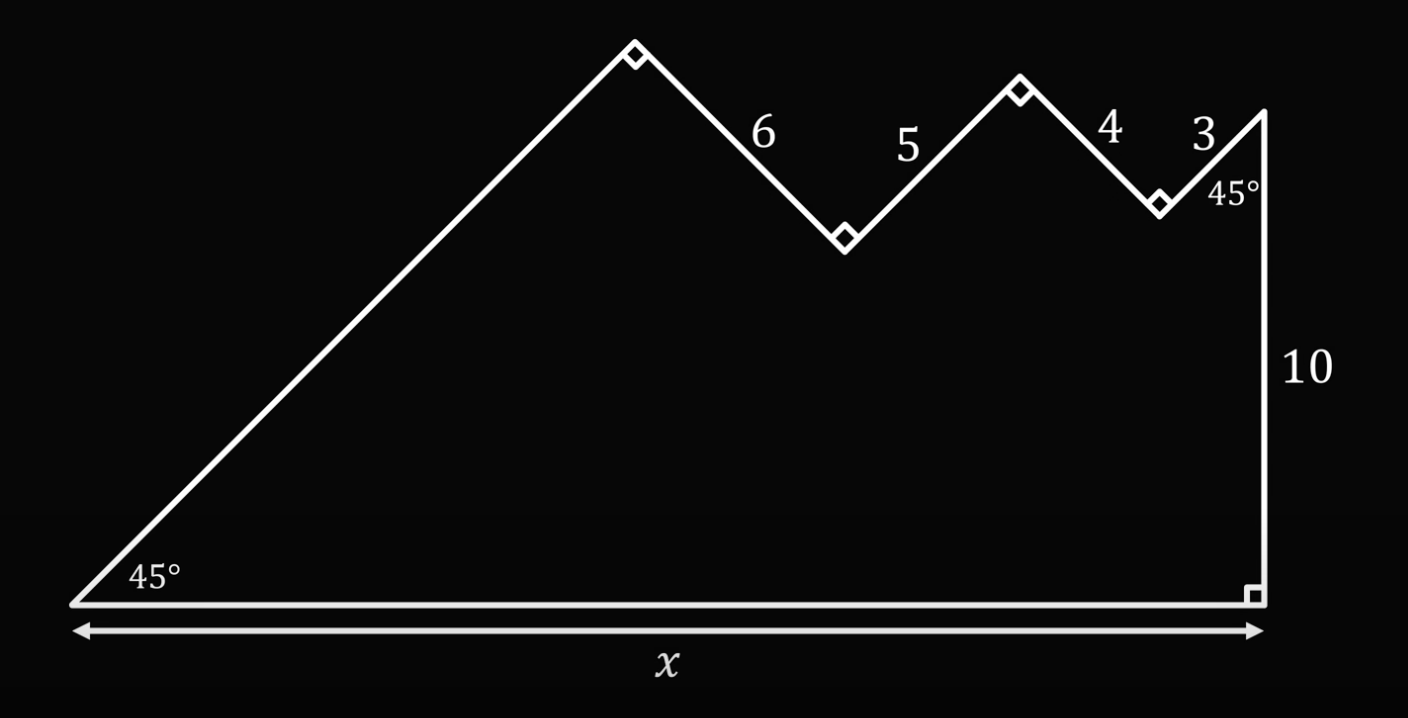
На самом деле эта задача решается довольно просто, если вспомнить школьную геометрию и свойства прямоугольных треугольников. Но чтобы ими воспользоваться, немного достроим рисунок.
Продолжим отрезок с длиной 5 до пересечения с основанием фигуры:
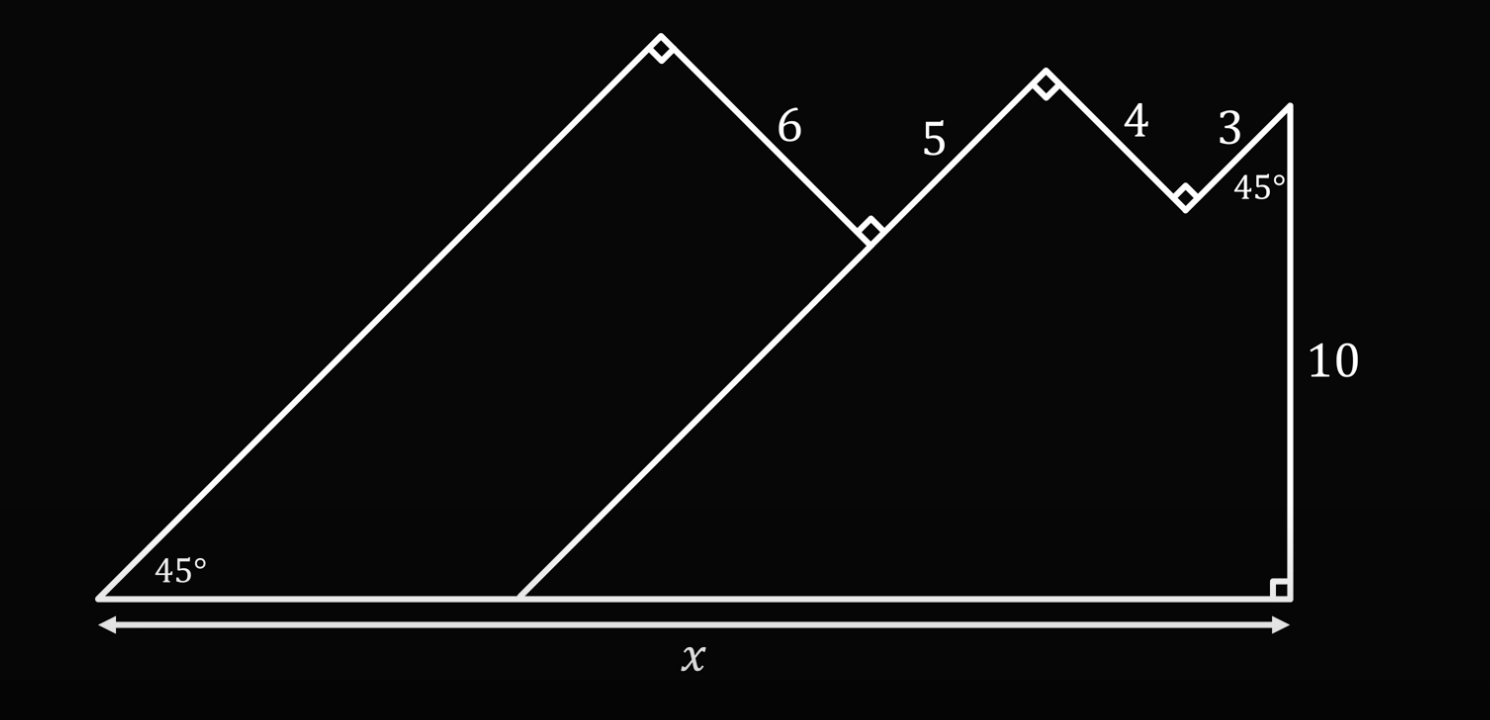
А теперь из точки пересечения проведём перпендикуляр, чтобы получить прямоугольник с короткой стороной, равной шести:
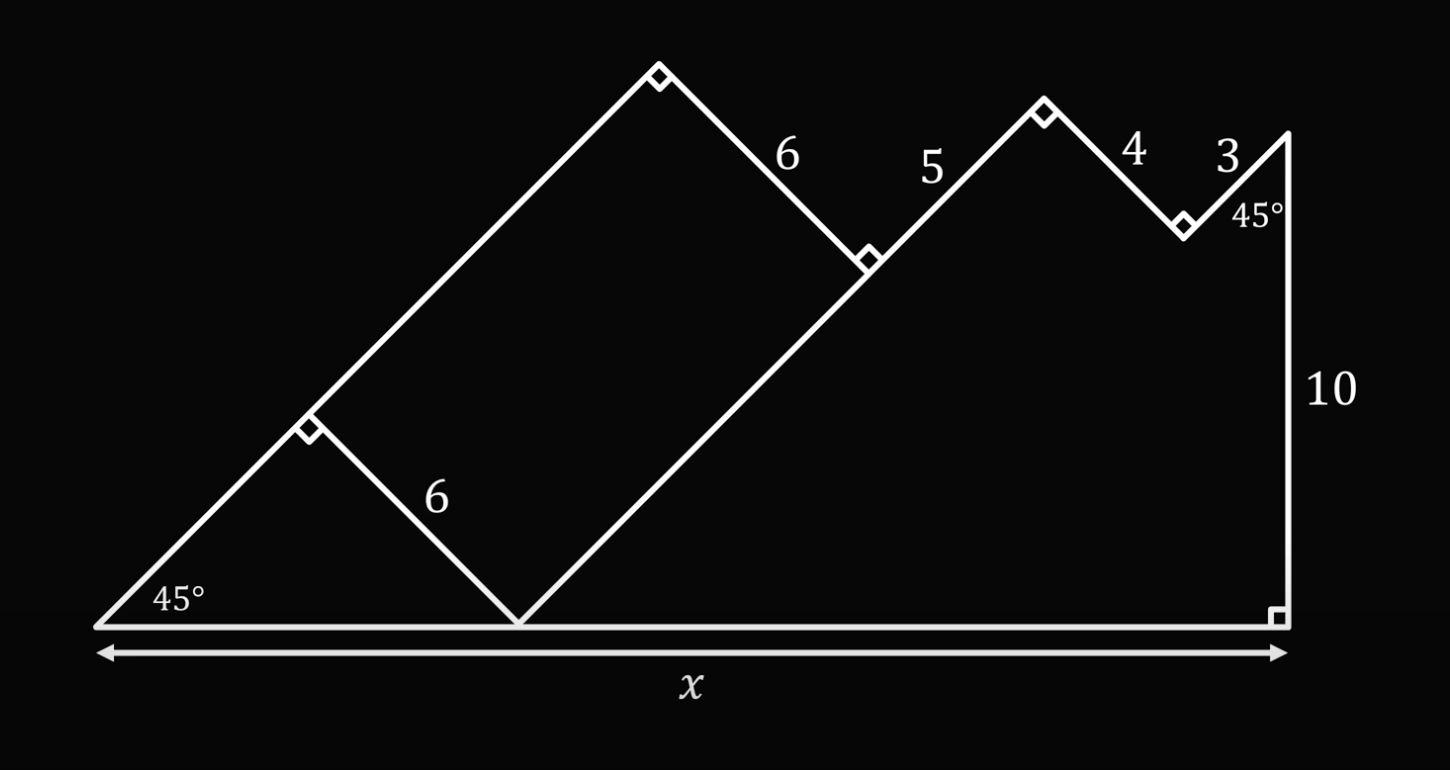
Точно так же поступим со вторым отрезком длиной 3 — продолжим его вниз до основания и проведём перпендикуляр:
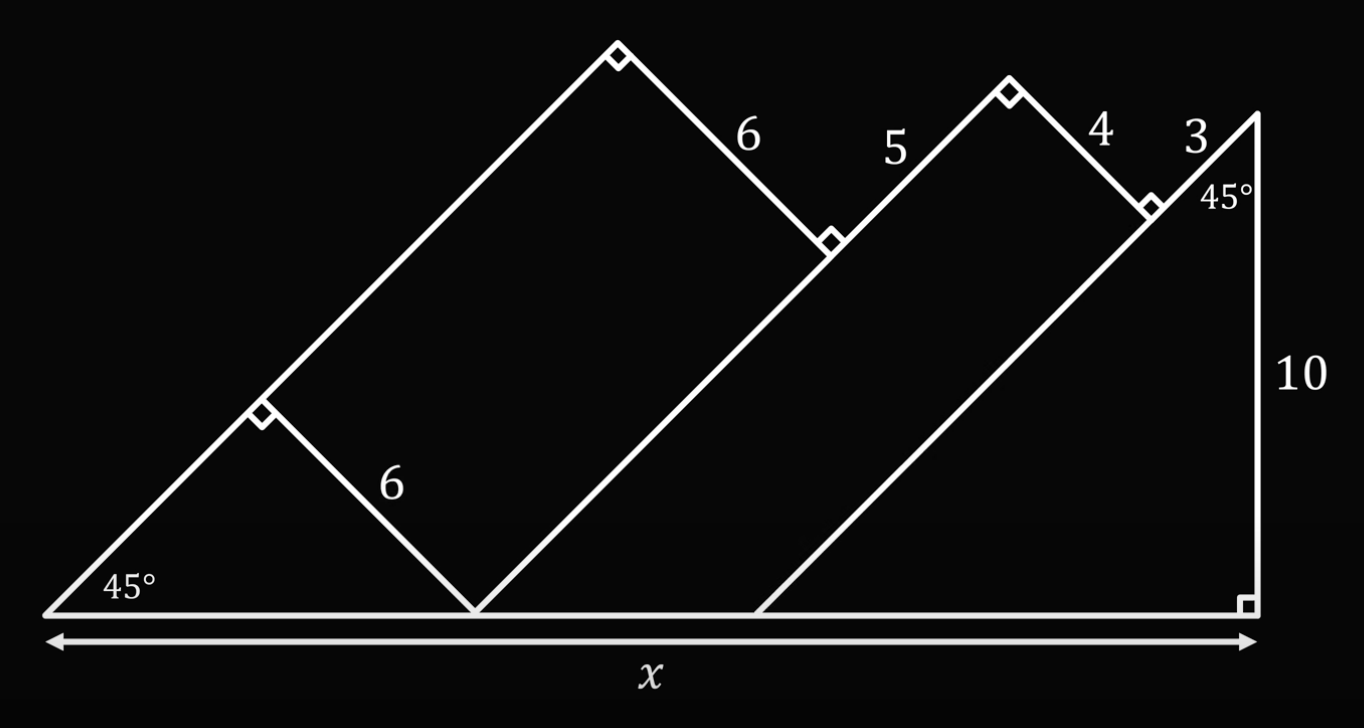
Так как мы получили снова прямоугольник, где противоположные стороны равны, то и новый отрезок тоже будет равен 4:
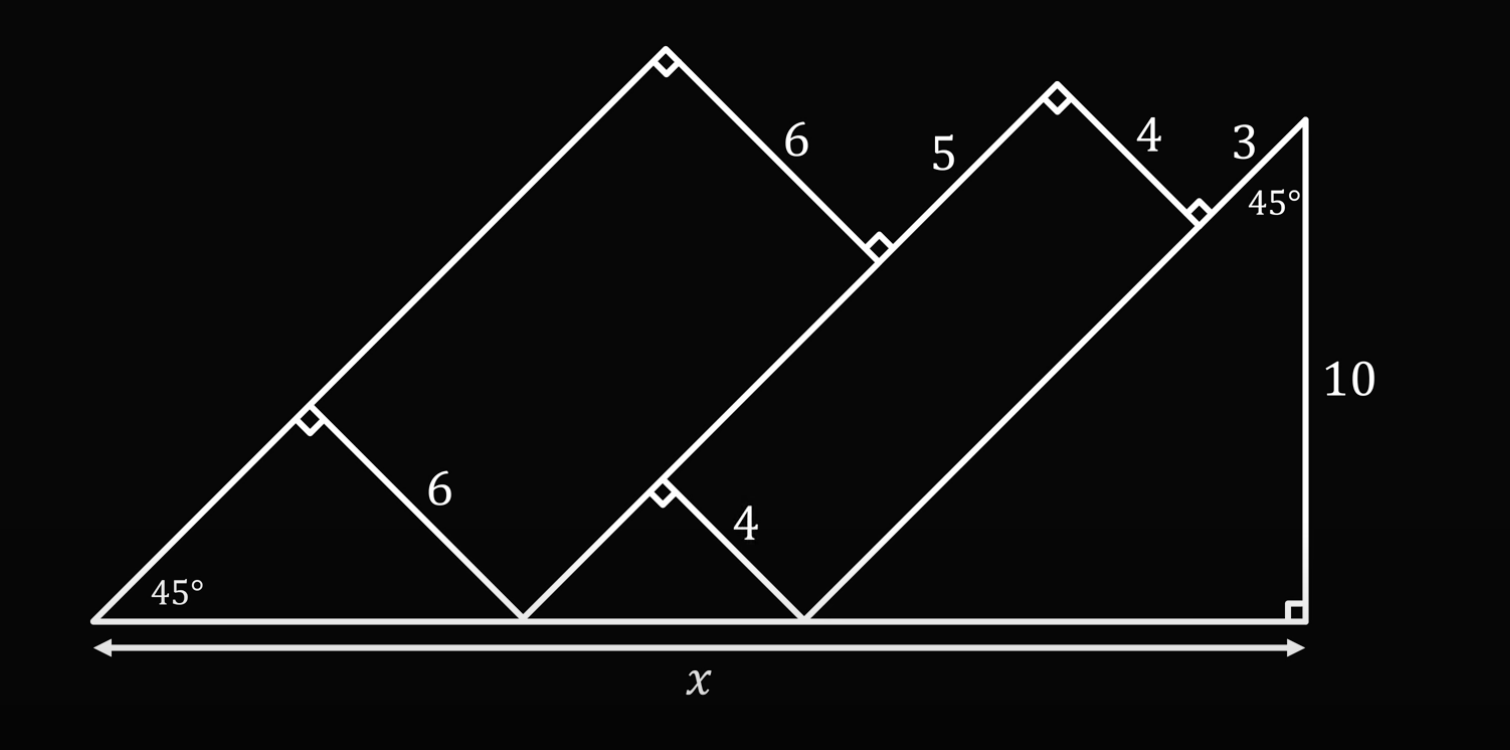
Теперь посмотрим на первый треугольник внизу, у которого одна сторона равна 6:
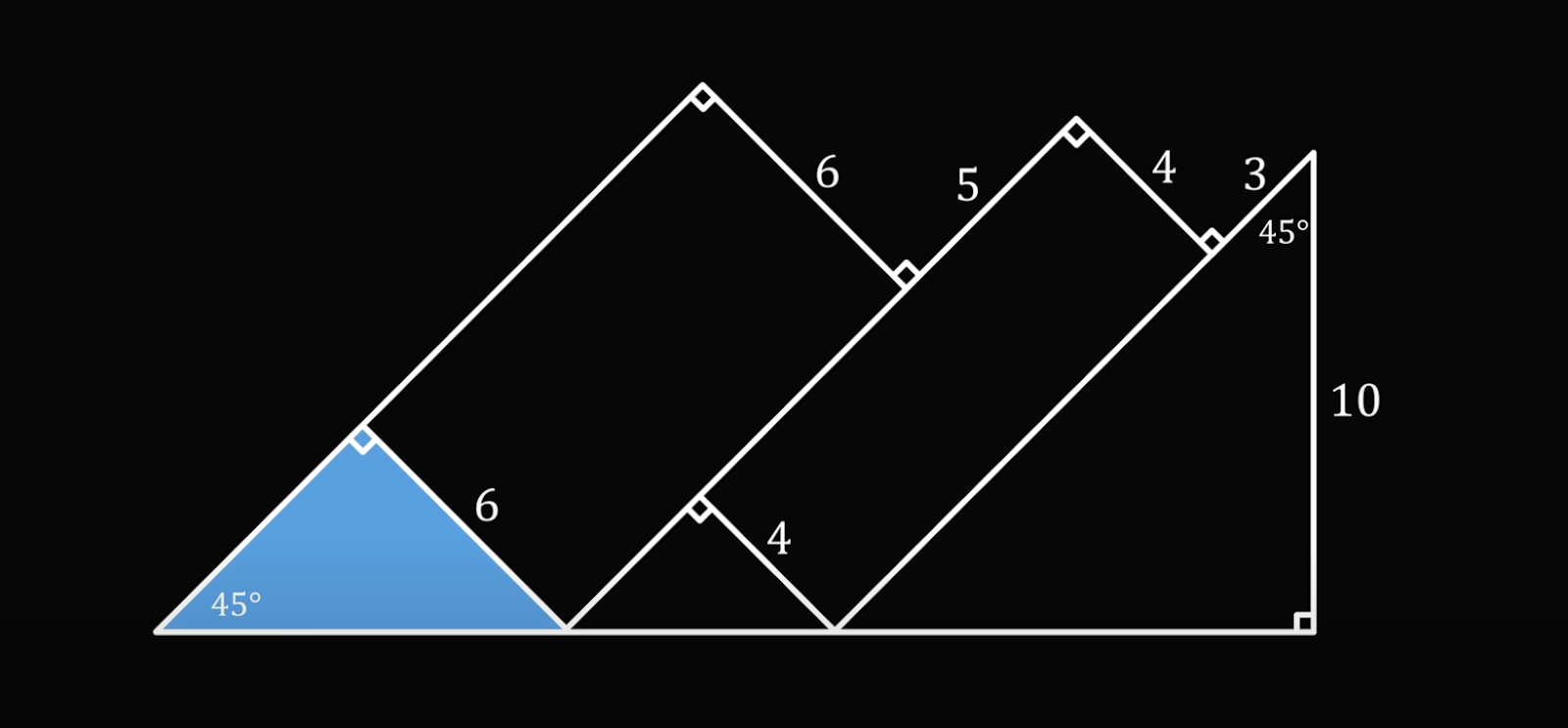
Раз один угол равен 45 градусам, а второй 90, то оставшийся угол тоже будет равен 45 (так как сумма углов в треугольнике равна 180 градусам). А раз два угла равны, то это равнобедренный прямоугольный треугольник, у которого левая сторона также равна 6.
Зная это, используем теорему Пифагора в общем виде:
x² + x² = c² → 2x² = c² → c = x√2
Здесь c — это основание нашего треугольника. Подставим вместо x шесть и получим его длину:
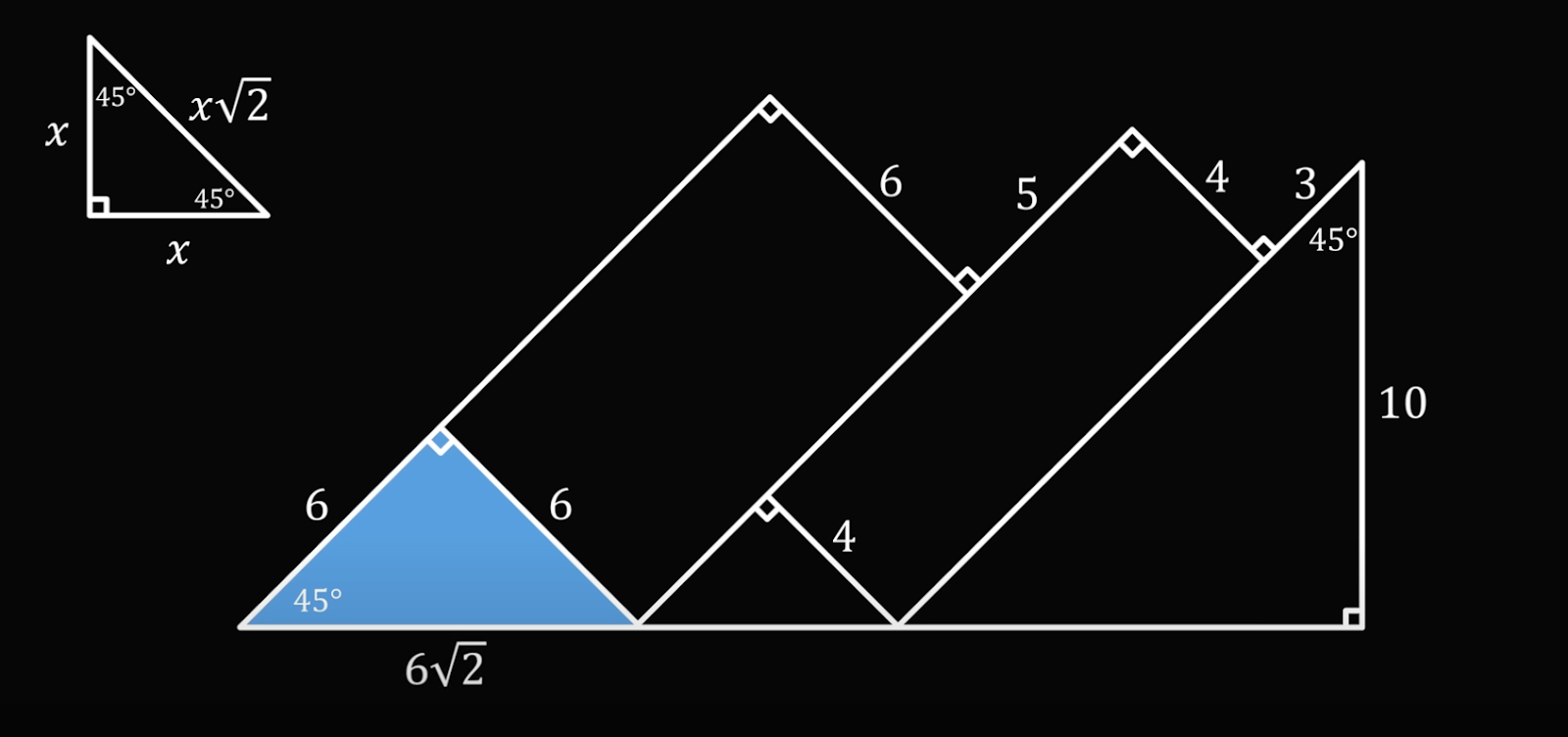
Проделаем это со вторым треугольником:
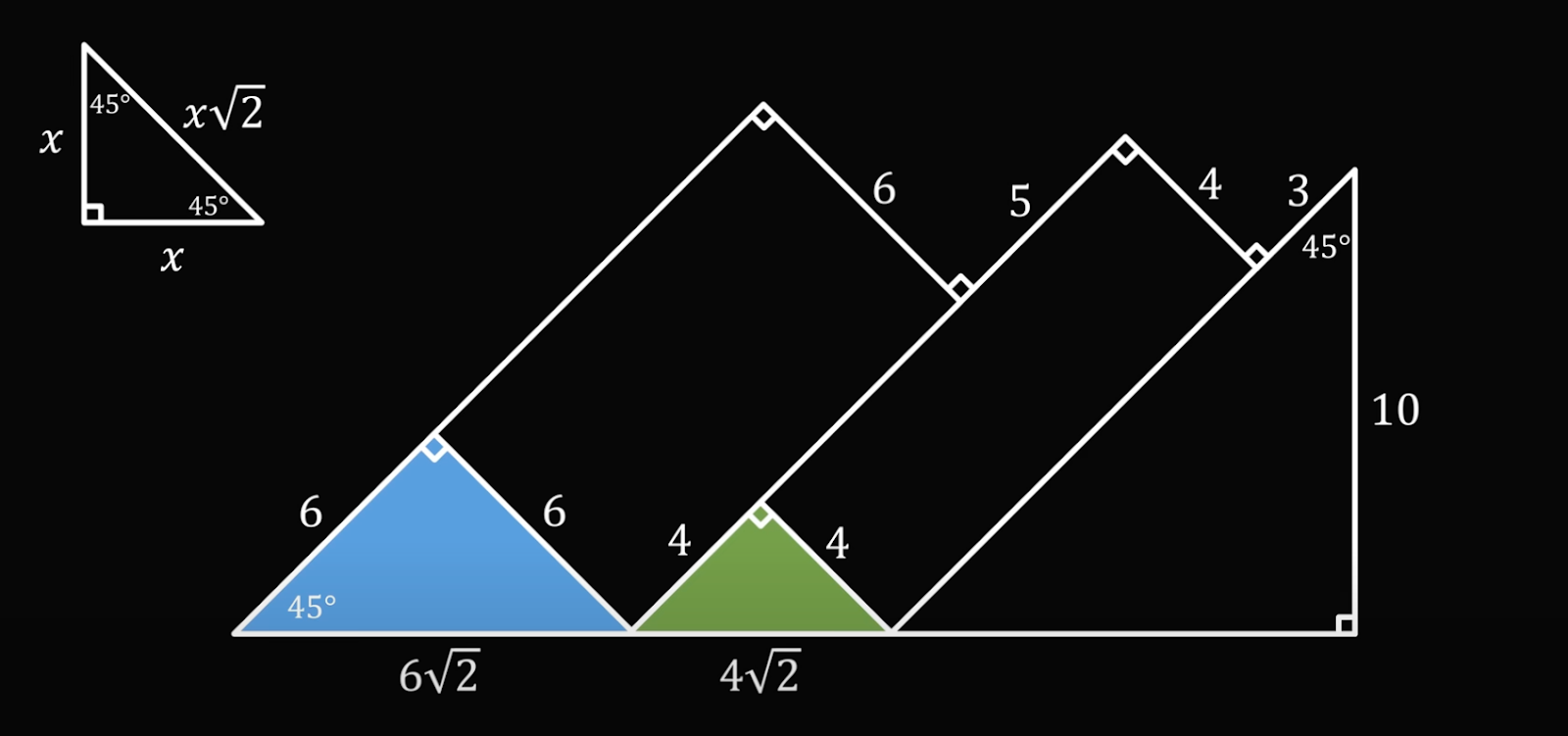
И наконец, посмотрим на третий треугольник:
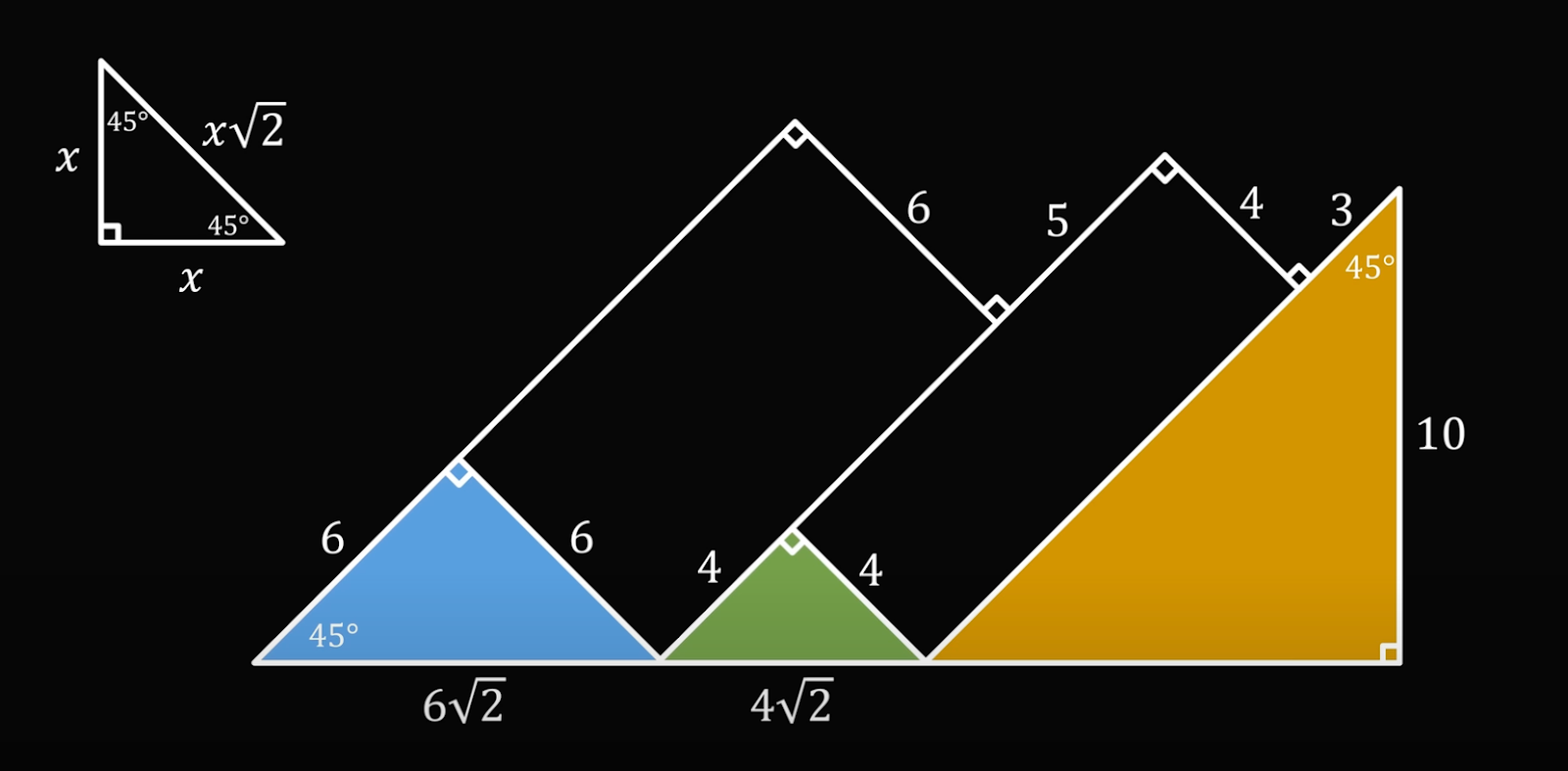
У него третий угол тоже равен 45 градусов (180 − 90 − 45 = 45), а это значит, что он тоже равнобедренный. Получается, что нижняя часть треугольника равна его правой части:
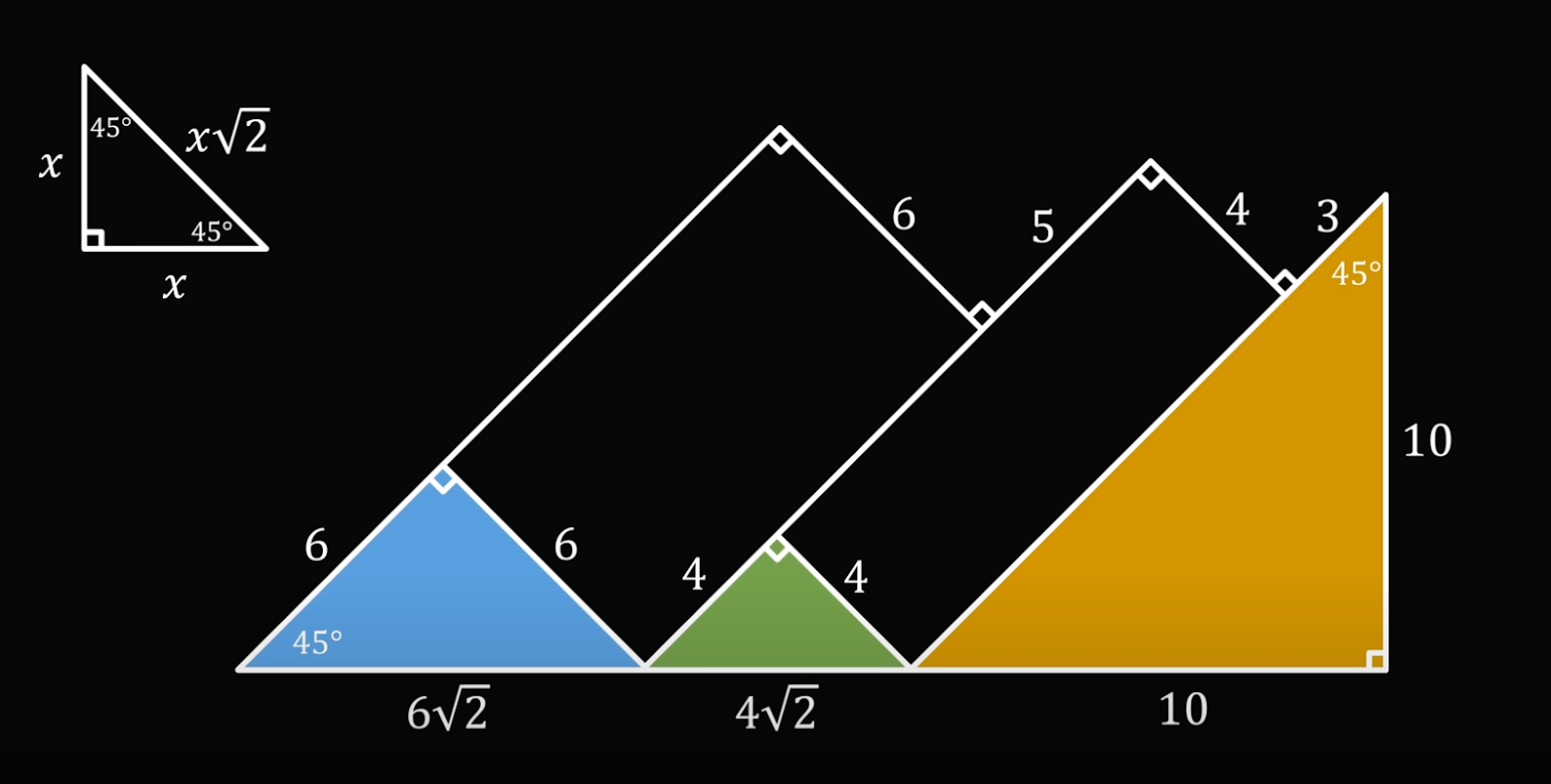
Чтобы найти общую длину основания горы, сложим все три числа:
6√2 + 4√2 + 10 = 10√2 + 10, а это примерно равно 24,14
Получается, что опытный программист был не прав, когда говорил, что не получится установить связь из-за того, что расстояние больше 25 километров.











