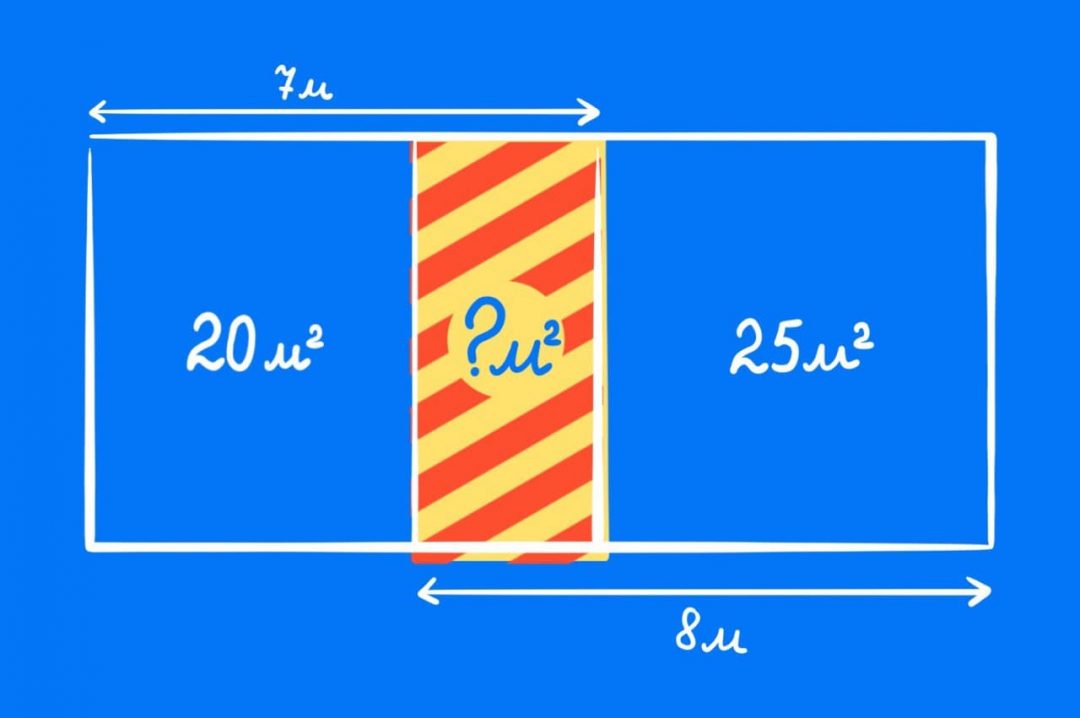
Старая задачка для тех, кто устал от сложных расчётов: найдите площадь маленького прямоугольника внутри большого прямоугольника (он выделен синим):
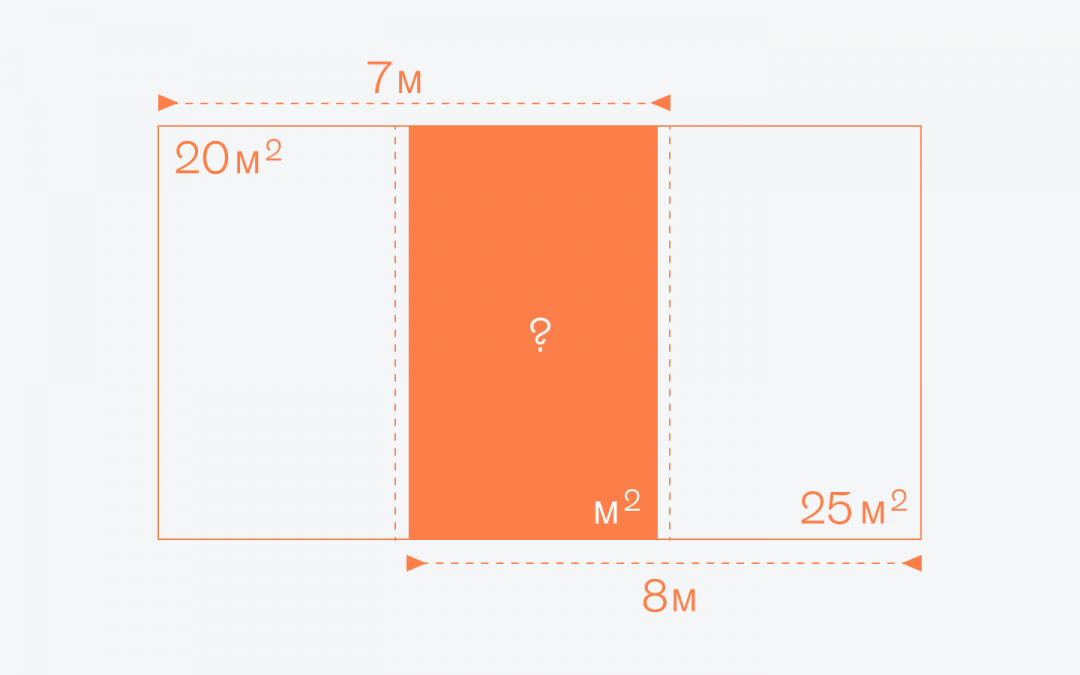
Чтобы решить эту задачу, обозначим ширину синего прямоугольника за X. Заодно уберём метры и квадратные метры, чтобы не мешали:
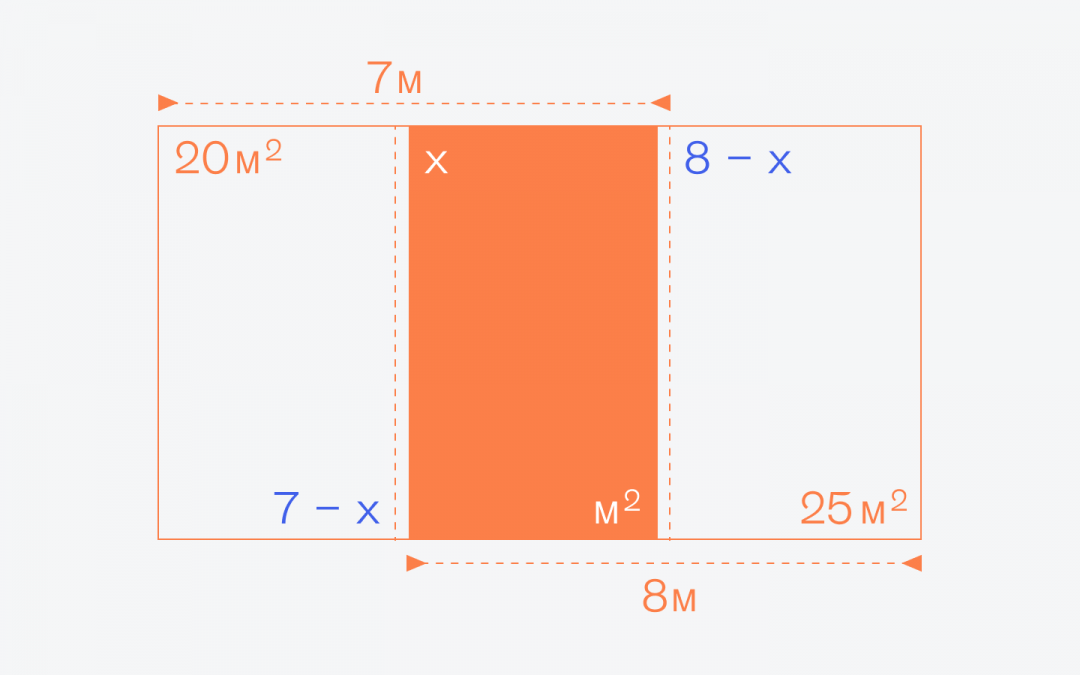
Отлично, у нас появилась ширина у тех прямоугольников, у которых известна площадь. Осталось добавить высоту Y — так как большая фигура тоже прямоугольник, то высота всех внутренних прямоугольников также будет одинаковой:
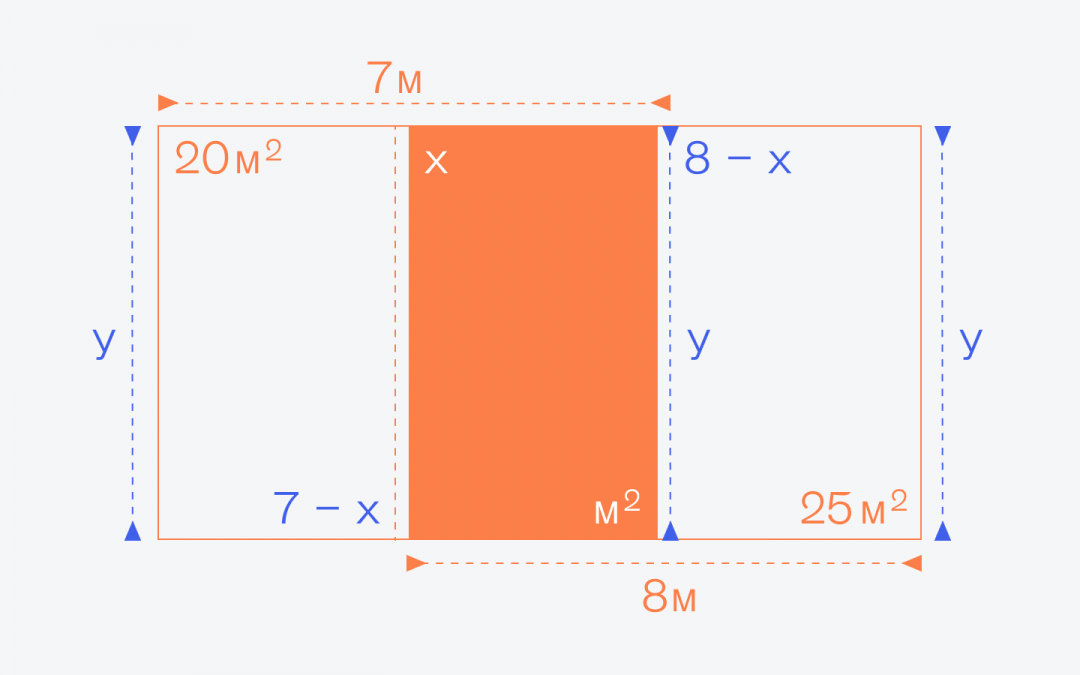
Теперь, когда у нас есть размеры и площади прямоугольников, мы можем составить два равенства:
(7 − x) × Y = 20
(8 − X) × Y = 25
Получилось два уравнения с двумя неизвестными, а значит, их можно объединить в систему и решить:
7Y − XY = 20
8Y − XY = 25
Вычтем первое уравнение из второго:
(8Y − 7Y) − (XY − XY) = 25 − 20
Y = 25 − 20 = 5.
Теперь подставим это значение в первое уравнение:
7 × 5 − 5X = 20
35 − 5X = 20 → 5X = 35 − 20 → 5X = 15 → X = 3.
В самом начале мы обозначили ширину синего прямоугольника за X, а потом высоту — за Y. Значит, его площадь будет равна X × Y. А раз мы уже знаем оба эти значения, то получается, что площадь синего треугольника равна 3 × 5 = 15 квадратных метров.