В последние дни года все настолько устали, что иногда не могут решить даже простые логические задачи. Если вы тоже устали, вы не сможете решить эти задачи. А если можете — то не устали и нужно ещё устать.
Уставайте вместе с нами.
Спор двух программистов
Один программист пришёл к другому и, немного выпив, говорит:
— Загадай любое натуральное число X!
— Отстань.
— Нет, загадай.
— Ну загадал.
— А теперь придумай три любых числа от 6 до 8 включительно.
— Придумал, и что дальше?
— А теперь умножь своё начальное число X на первое из них, прибавь второе и отними третье. Сколько у тебя получилось?
— Минутку… 164.
— Ха, а я знаю, какие ты числа загадал!
— Что, все четыре числа вычислил?!
— Ага!
— НО КАК?!
Действительно, как первому программисту удалось узнать все числа, которые загадал второй?
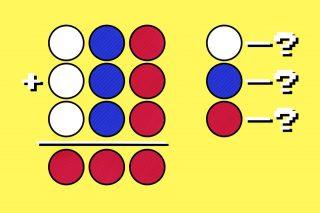
Обозначим три загаданных числа от 6 до 8 как A, B и C. Если мы сделаем всё, как написано в задаче, то получим равенство: A × X + B − C = 164.
Из этого получим X:
X = (164 − B + C) / A
Исключаем число 7
Если A = 7, то числитель нашей дроби должен нацело делиться на 7, потому что X не может быть дробным (по условию X — натуральное число). Числа, близкие к 164, которые делятся на 7 — это 161 и 168.
Чтобы получить 161 в числителе, числа B и C должны отличаться друг от друга на 3, а это невозможно, потому что максимальная разница равна 8 − 6 = 2.
Чтобы получить 168 в числителе, числа B и C должны отличаться друг от друга на 4, а это тоже невозможно, потому что максимальная разница равна 8 − 6 = 2.
Значит, A точно не равно 7. Запомним это.
Если число A точно не 7, то оно чётное — 6 или 8. Это значит, что числитель (164 − B + C) тоже чётный, чтобы в результате деления получилось целое число. А это возможно, если числа B и C оба чётные или оба нечётные.
Если числа B и C оба нечётные, то это возможно только в случае, если они оба равны 7. В этом случае −B + C = 0, и в числителе остаётся только 164, которое нам предстоит разделить на 6 или 8. Но 164 не делится нацело ни на 6, ни на 8, значит, они тоже не равны 7.
Исключаем одинаковые B и C
Из последнего примера мы видели, что B и С не могут быть одинаковыми в принципе, неважно, чётными или нечётными, поэтому остаются только два варианта:
B = 6, C = 8 или B = 8, C = 6.
Проверяем оставшиеся варианты
Если B = 6 и C = 8, то в числителе получается так: (164 – 6 + 8) = 166. Но 166 не делится нацело ни на 6, ни на 8 (возможные значения A), значит, этот вариант можно исключить.
Получается, что остаётся только пара B = 8 и C = 6: (164 – 8 + 6) = 162. Число 162 нацело делится только на 6: 162 / 6 = 27, значит, A = 6, а второй программист загадал число 27:
X = 27
A = 6
B = 8
C = 6
Проверяем: 6 × 27 + 8 − 6 = 164. Всё сходится.
Как угадать число от 0 до 100 за 7 попыток?
Программист развлекает сына:
— Загадай любое целое число от 0 до 100!
— Загадал.
— Спорим, я угадаю его за 7 попыток или быстрее? Я буду называть числа, а ты — отвечать, оно больше, меньше или равно загаданному.
— Ахахах, ты не сможешь угадать за 7 попыток!
— Спорим, угадаю!
— Ну давай, покажи своё кунфу…
6 попыток спустя отец угадал число, а ребёнок сидит в шоке. Они попробовали снова, и во второй раз отец угадал число за семь попыток. В третий — за четыре. Сколько бы они ни играли, число всегда угадывалось за 7 попыток или менее.
Вопрос: как?
Это простейшая алгоритмическая задача, которую показывают на первом уроке информатики, чтобы показать мощь алгоритмического мышления. Смысл в том, чтобы...
👉 каждый раз называть число, которое делит пополам диапазон возможных чисел.
Этот приём каждый раз в два раза сокращает область поиска, и в конце нам становится легко угадать даже простым перебором.
Допустим, сын загадал число 63. Тогда делаем так:
- Находим середину диапазона от 0 до 100 — это 50. Называем это число. Сын говорит «Больше».
- Значит, его число лежит в диапазоне от 50 до 100. Находим его середину — 75. Называем это число. Сын говорит «Меньше».
- Ага, значит, его число находится в диапазоне от 50 до 75. Находим середину — 62. Называем это число. Сын говорит «Больше».
- Поиск снова сузился: от 62 до 75. Середина — 67. Называем это число. Сын говорит «Меньше».
- У нас осталось 3 попытки и 4 числа. Найдём ещё одну середину — 64. Называем это число. Сын говорит «Меньше».
- Раз у нас число, которое больше, чем 62, и меньше, чем 64, то это число 63. Даже седьмая попытка не понадобилась.
Этим способом можно угадать любое число от 0 до 100 за 7 попыток или меньше. Главное — быстро и правильно считать в уме середину и помнить, как выглядит сейчас твой рабочий диапазон.
А если число будет больше?
На самом деле за 7 шагов можно угадать любое число от 0 до 127 или от 1 до 128. Всё потому, что два в седьмой степени — это как раз 128. Каждый раз, когда мы делим рабочий диапазон на 2, мы как будто убираем одну степень у двойки, постепенно уменьшая наш диапазон угадывания до двух чисел. Для верности лучше добавить ещё попытку.
Если бы у нас было 8 попыток, можно было бы угадывать числа до 256. 9 попыток — 512 и так далее.
А где это используется в народном хозяйстве?
На этом принципе построена модель данных «Бинарное дерево» — это одна из важнейших технологий для составления словарей и поиска данных. Прочитайте об этом в статье про бинарные деревья.
Сложная задача про светодиоды
Стартапер из Кремниевой долины отправился в Китай, чтобы найти производителей для своего нового хайтек-продукта. Проделав путь в тысячу вёрст, он наконец оказался на старом китайском рынке радиодеталей. В самом сердце рынка ему встретился мудрец Синьхуа. Он был известен как лучший вендор электроники и железа провинции Гуандун. Мудрецы говорили: «Если твоим проектом занялся Синьхуа, твоим инвестором станет Бог».
Синьхуа сидел за большим деревянным столом и сортировал светодиоды из большого мешка.
— О великий Синьхуа, — начал стартапер, — позволь представить взору твоему CAD-файлы моего будущего проекта!
Синьхуа посмотрел на него с прищуром и молвил:
— Если человек при первой встрече готов раскрыть CAD-файлы, он либо стартапер, либо глупец. Но работа с глупцами подобна супу из летучей мыши. Поэтому у меня для тебя загадка. Разгадаешь её — возьму твой проект на свой завод. А не разгадаешь — отправишься в Хабаровск писать код на языке 1С. Идёт?
Стартапер согласился.
Синьхуа достал два стакана: побольше и поменьше.
— В стакан побольше помещается 90 светодиодов. В стакан поменьше — 50 светодиодов. Вот тебе мой мешок светодиодов. Отмерь мне ровно 30 светодиодов, используя только эти два стакана. Считать вручную нельзя. Ежели справишься за 7 пересыпаний или меньше, возьму твой проект. А ежели нет…
Как думаете: справится стартапер с задачей на пересыпание за 7 ходов или поедет в Хабаровск писать конфигурации для 1С?
Чтобы было наглядно и понятно, что куда пересыпается, нарисуем всё картинками:
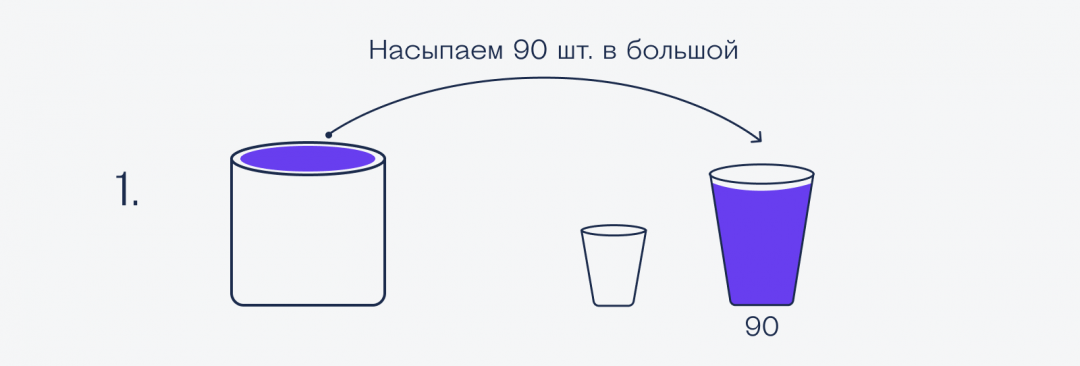
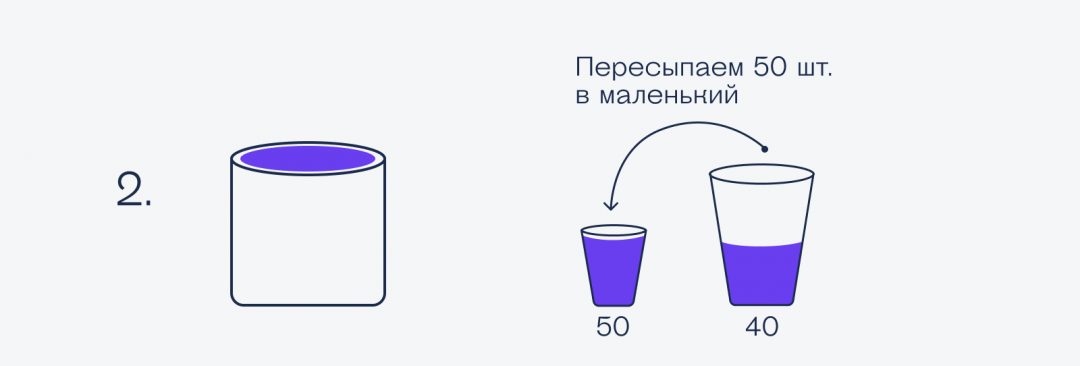
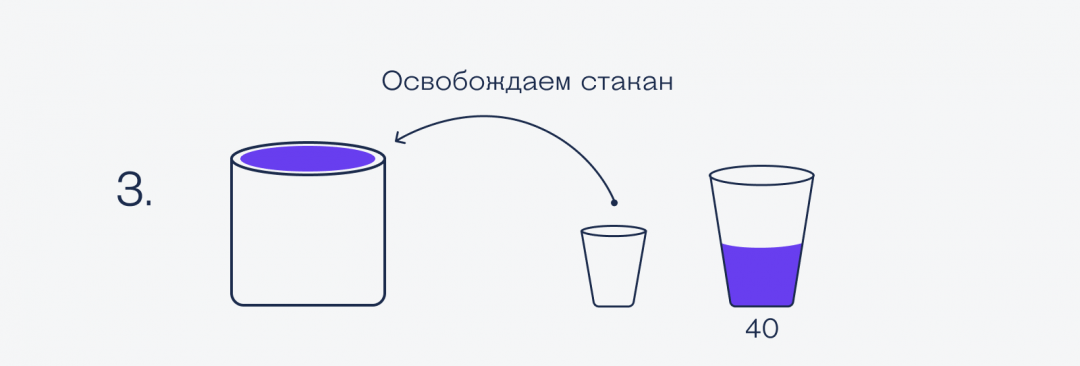

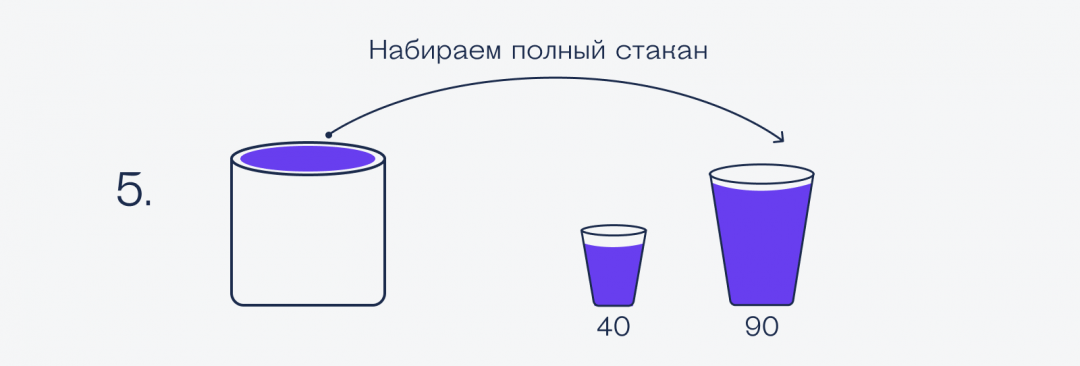

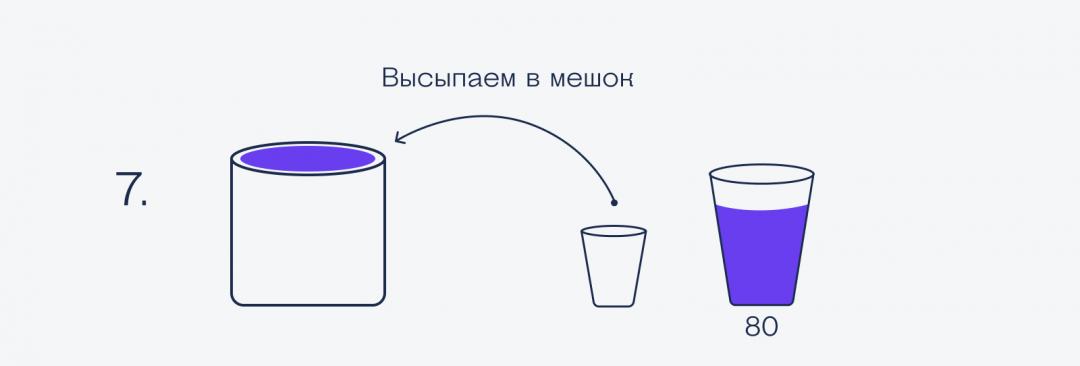

Получается, что на всё потребовалось 8 пересыпаний, а не 7. А раз по условиям нужно было всё успеть за 7 пересыпаний или меньше, наш стартапер проиграл и поедет в Хабаровск.
Сложная задача про поросёнка и NFT
Это классическая задача на логику и экономику. Большинство людей не могут правильно решить её с первого раза, потому что логика взрывает мозг. Проверьте, насколько ваш мозг взрывоустойчивый.
NFT-трейдер купил редкий токен на картинку с поросёнком, сумма сделки составила 6 тысяч долларов. Через время он продал токен за 7 тысяч, но передумал и выкупил обратно за 8 тысяч. Ещё через какое-то время он продал этот токен за 9 тысяч долларов.
Вопрос: сколько денег в итоге заработал или потерял трейдер на этой цепочке сделок?
Неправильное решение
Иногда эту задачу решают так:
потратил 6 (−6), потом заработал 7 (+7), потом потратил 8 (+8), а потом заработал 9 (+9), но раз после последней продажи он остался без токена, который изначально стоил 6, то он ещё потерял 6 (−6):
−6 + 7 − 8 + 9 − 6 = −4 тысячи долларов.
❌ По этой логике трейдер потерял за все эти сделки 4 тысячи долларов, но это явно неверное решение.
Правильное решение
Задачу легко решить, если правильно определить исходную точку. А она такая: когда трейдер покупает токен, это не трата, а его цель, за которой он пришёл. На старте у него есть 6 тысяч долларов, а остальное зависит от продавцов.
На первом шаге он покупает токен за 6 тысяч, и его баланс равен −6 тысяч.
На втором шаге он продаёт его за 7 тысяч, и его баланс становится равен −6 + 7 = 1 тысяча.
На третьем шаге трейдер покупает токен назад за 8, и его баланс равен 1 − 8 = −7 тысяч.
А на четвёртом он продаёт токен обратно и получает за это 9 тысяч, и итоговый баланс становится равен −7 + 9 = 2 тысячи.
Подвох с пропавшей тысячей
🤔 Кажется, что задача решена, но если трейдер в плюсе на 2 тысячи и пришёл на криптобиржу с 6 тысячами на счёте, то у него должно быть 8 тысяч. Но за последнюю продажу он получил 9 тысяч и с ними и остался — куда же тогда делась ещё тысяча?
✅ А тысяча делась на возврат долга самому себе, когда трейдер выкупал обратно свой же токен на тысячу дороже, чем он стоил:
- Купил за 6 тысяч ← денег стало 0 (условно, на самом деле мы не знаем, сколько денег у него было на счёте).
- Продал за 7 тысяч ← появились 7 тысяч.
- Купил за 8 тысяч ← а вот здесь как раз не хватает той тысячи, которую нужно у кого-то занять, чтобы выкупить токен.
- Продал за 9 тысяч ← появилось 9 тысяч, возвращаем 1 тысячу долга.
Индийская задача про деньги и баланс
Эта задача пришла к нам в прошлом году из индийских соцсетей, поэтому в ней лихой сюжет и неожиданная развязка.
В одной индийской компании программист в обед услышал громкие крики и причитания из бухгалтерии. Оказывается, в программе, которую сделал этот программист, есть две колонки — «Потрачено» и «Остаток». Но из-за странной ошибки у бухгалтера не сходится баланс.
Началось всё так: компания выдала менеджеру 50 тысяч на закупку товаров, а каждый расход заносился в программу. Первая покупка вышла в 20 тысяч, и это сразу отразилось в таблице:

После этого менеджер сделал ещё три покупки, которые тоже сразу отправились в отчётную таблицу:
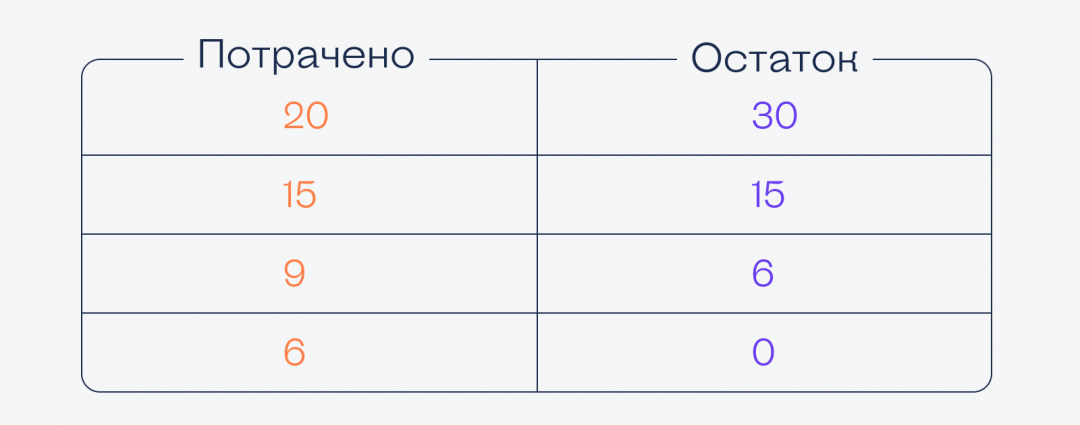
Но когда программа сложила числа в столбцах, то выяснилось, что суммы различаются и откуда-то взялась лишняя тысяча. В чём ошибка?
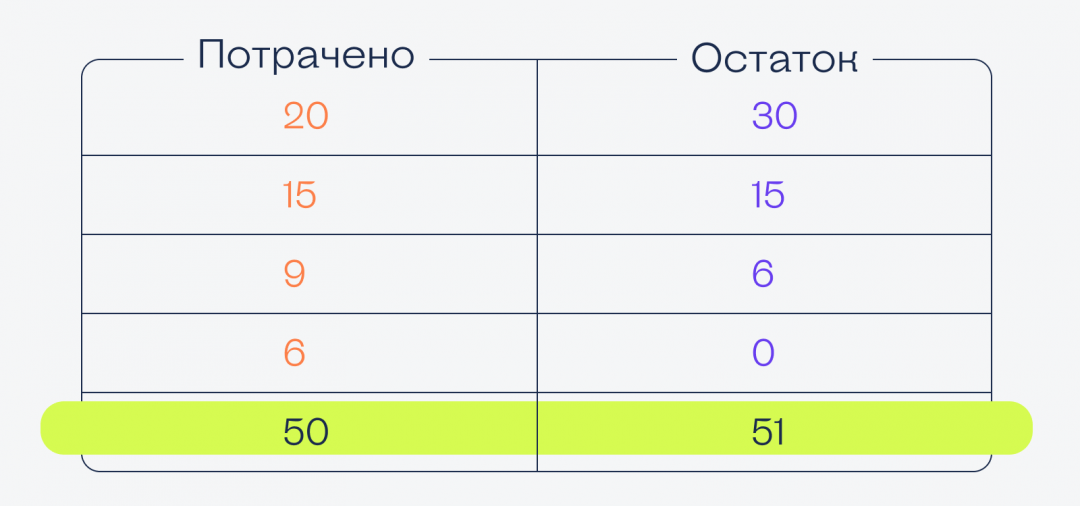
С точки зрения математики, в этой задаче всё верно — в обоих столбиках сумма посчитана правильно, подвоха здесь нет.
Но проблема в том, что в этой задаче не имеет смысла складывать содержимое столбца «Остаток». Имеет смысл считать только потраченные деньги.
Столбец «Остаток» показывает лишь количество оставшихся денег после всех предыдущих операций и служит показателем лимита расходов. А правильные операции с использованием остатка выглядят так:
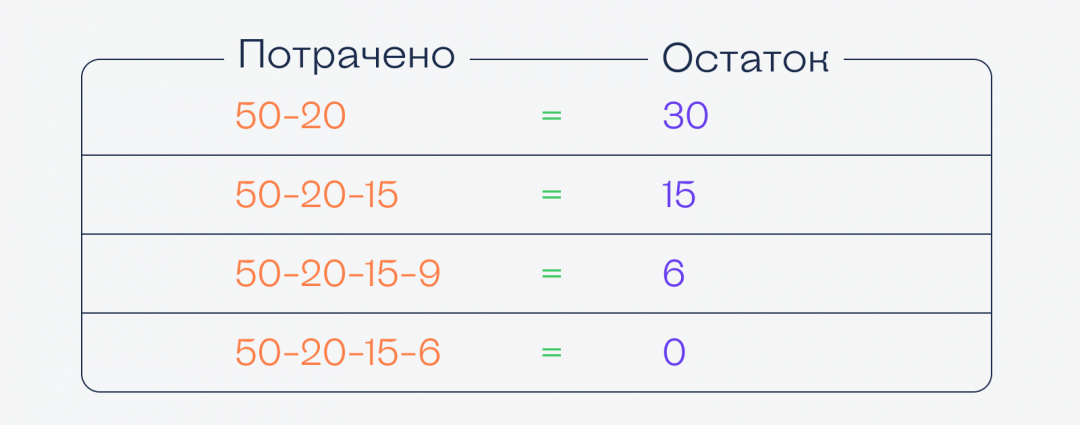
Как это проверить: попробуйте потратить первым действием потратить не 20 тысяч, а два раза по 10 тысяч. В «Остатке» вы получите сначала 40, потом 30. В сумме это уже даст 70, хотя мы не потратили даже половину.
Или попробуйте последнее действие (когда тратили 6 тысяч) разделить на 6 действий по одной тысяче. В остатке вы получите 5, 4, 3, 2, 1 и 0. В сумме это 15, хотя потратили мы только 6.
Короче: суммировать остатки некорректно. Это не «Дебет» и «Кредит», это другое.
То, что в исходной задаче в «Остатке» появилась дополнительная тысяча, — не более чем способ запутать обывателя. Мы намеренно каждый раз вычитаем всё меньшие числа, чтобы было ощущение, что остаток и потраченная сумма как-то связаны. А они не связаны.
Теперь, когда вы это знаете, попробуйте загадать эту задачку своим коллегам и родственникам и посмотрите, сколько времени им понадобится, чтобы получить правильный ответ :-)
Сколько нужно ленты для передачи данных?
Перед вами очередная задача для детей, которая неожиданно ставит в тупик большинство взрослых. Попробуйте решить её сами, а потом проверьте себя, заглянув в решение.
Вот задача:
В петербургском НИИ разрабатывают систему обмена короткими текстовыми сообщениями с помощью ЭВМ. Так как интернет не работает, сообщения записывают на магнитные ленты, запечатывают в конверты и отправляют на абонентский ящик получателя.
Лаборант Сергей попросил завлаба выделить 200 одинаковых ленточек по 110 сантиметров, чтобы закодировать на них старый советский анекдот и разослать всем друзьям.
Завлабу понравился анекдот, и он отправил лаборанта в магазин, чтобы тот купил нужное количество магнитной ленты. В магазине выяснилось, что лента продаётся в бобинах по 25 метров.
Вопрос: сколько бобин нужно купить лаборанту, чтобы хватило на рассылку анекдота всем друзьям? Учтите, что склеивать две ленты в одну целую нельзя.
Большинство детей и их родителей решают эту задачу так:
- Длина каждой ленты — 110 сантиметров, или 1,1 метра.
- Всего нам требуется 200 лент, значит, нужно умножить 1,1 на 200 — так мы получим общую длину лент, которую нужно купить.
- 1,1 × 200 = 220 метров ленты — сколько нужно для рассылки анекдота.
- Раз в бобине 25 метров, то разделим 220 метров на 25 — так мы получим количество бобин: 220 / 25 = 8,8 бобины.
- Но так как бобины продаются целыми и поштучно, то округлим 8,8 до следующего числа — получим 9 бобин. Этого точно хватит.
Но это неправильное решение, и если купить всего 9 бобин, то их не хватит для рассылки. Почему так — смотрите в правильном решении.
На самом деле нам не нужна общая длина лент для кодирования анекдота — вместо этого нам нужно посчитать, сколько таких лент можно сделать из одной бобины.
- Длина каждой ленты — 110 сантиметров, или 1,1 метра.
- В бобине 25 метров, значит, чтобы узнать, сколько лент мы можем сделать из одной бобины, нужно разделить 25 на 1,1.
- 25 / 1,1 = 22,72. Получается, что из одной бобины можно сделать 22 ленты и останется ещё какой-то короткий отрезок. Он нам не пригодится — мы не сможем сделать из двух отрезков ещё одну ленту, потому что данные на такую ленту записать невозможно.
- Раз из одной бобины получается 22 ленты, а нам нужно всего 200 лент, то разделим 200 на 22, чтобы узнать, сколько бобин нам нужно.
- 200 / 22 = 9,09 бобины. Но так как бобины продаются целыми и поштучно, то округлим 9,09 до следующего числа — получим 10 бобин.
Получается, что если решить эту задачу неправильно, то лаборанту придётся идти в магазин ещё за одной бобиной (или кто-то из друзей не получит рассылку с советским анекдотом). А всё потому, что кто-то поторопился с решением.
Сложная задачка на логику и математику: пассажиры в вагоне
Чтобы поддержать внутренний туризм, команда программистов купила билеты на поезд по Золотому кольцу и заняла все места. Всего в поезде было 11 вагонов и 381 место.
В разных вагонах ввиду конструкционных особенностей разное количество мест и, соответственно, разное количество пассажиров. Но в каждых любых трёх вагонах подряд в сумме едет ровно 99 человек. Какие бы три вагона подряд ни взяли — всё равно 99.
Сколько человек едет в девятом вагоне?
Пронумеруем вагоны и обозначим каждый вагон своей переменной. Когда мы их сложим, то получим 381:
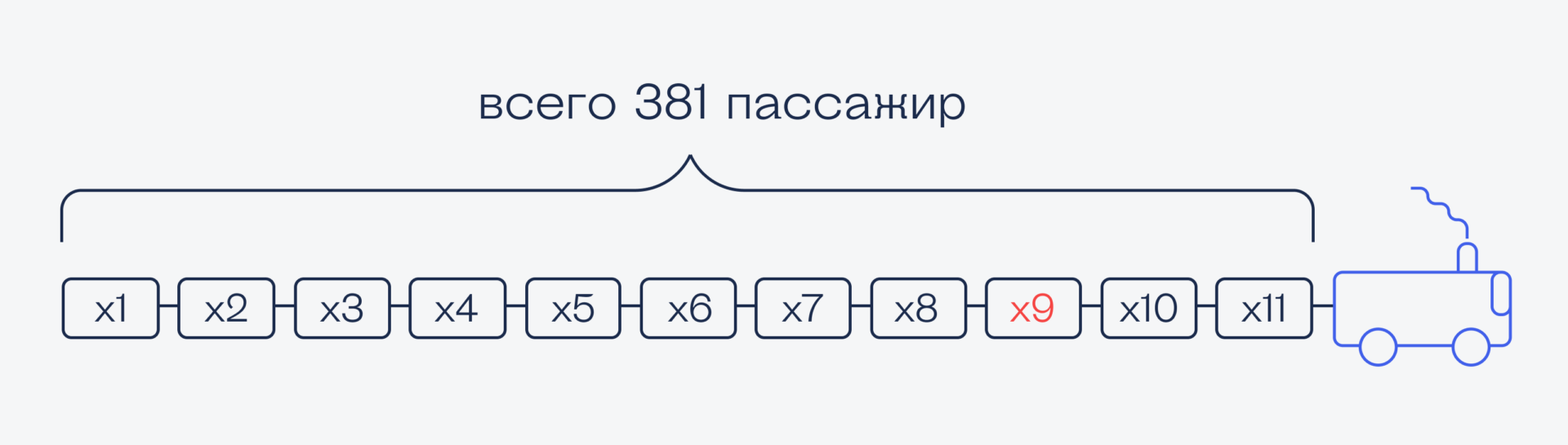
x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 = 381
По условию три любых вагона подряд дают в сумме 99. Это значит, что:
x1 + x2 + x3 = 99
x4 + x5 + x6 = 99
x7 + x8 + x9 = 99
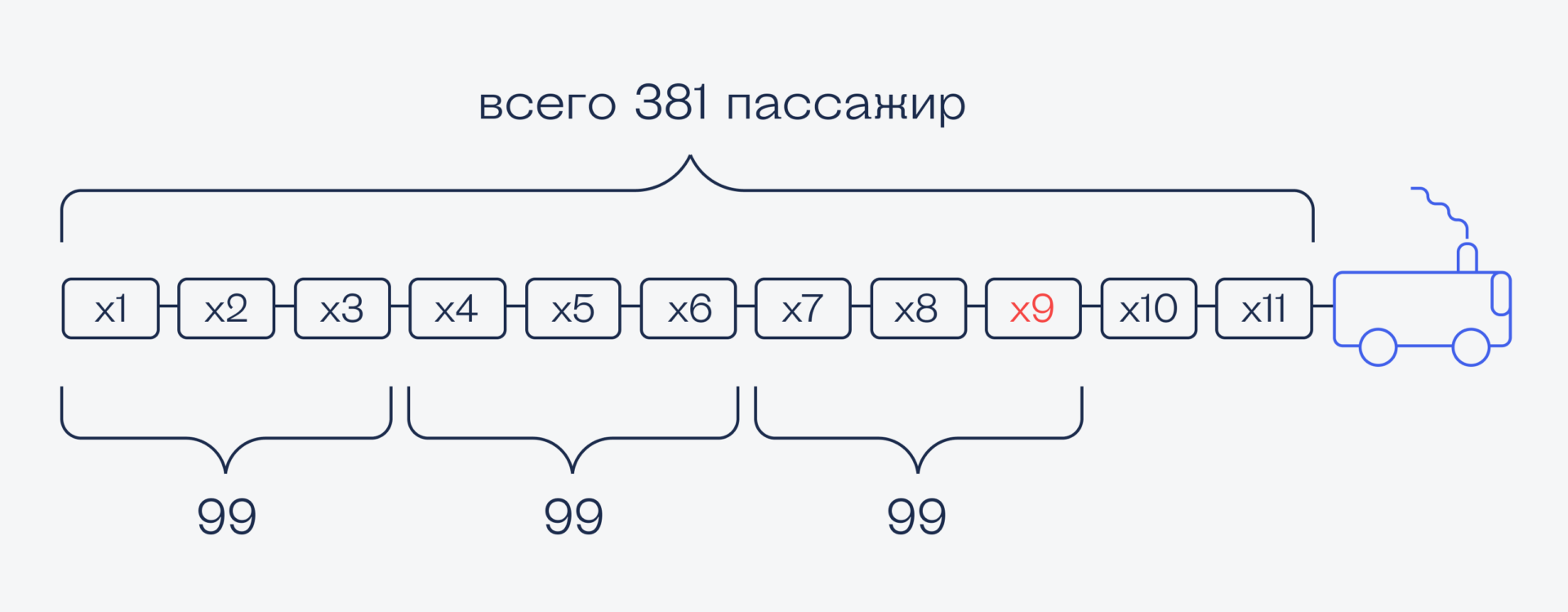
Заменим эти переменные на числа:
(x1 + x2 + x3) + (x4 + x5 + x6) + (x7 + x8 + x9) + x10 + x11 = 381
99 + 99 + 99 + x10 + x11 = 381
297 + x10 + x11 = 381
x10 + x11 = 84
С другой стороны, по условию в трёх последних вагонах тоже едет в сумме 99 пассажиров:
x9 + x10 + x11 = 99
Вычтем отсюда предыдущее уравнение:
(x9 + x10 + x11) − (x10 + x11) = 99 − 84
x9 + x10 − x10 + x11 −x11 = 15
x9 = 15
Получается, что в девятом вагоне едет 15 человек. Кстати, в третьем вагоне тоже 15 человек, потому что он девятый с конца.
Задача про номер дома
На обеденном перерыве, когда было совсем жарко, один программист решил поиздеваться над другим. Он сказал:
— Я загадал два разных числа от 1 до 9, сможешь угадать их сумму?
— Да ну, ты чего, там же куча вариантов.
— Окей, дам подсказку: последняя цифра в произведении моих чисел такая же, как номер моего дома.
— Так я же не знаю номер твоего дома. Хотя подожди, я понял!
И второй программист сразу же назвал сумму двух загаданных чисел. Как он это сделал?
Так как второй программист понял, как решить эту задачу только после информации о произведении чисел, сделаем то же самое: посмотрим, чему равно произведение всех чисел от 1 до 9:
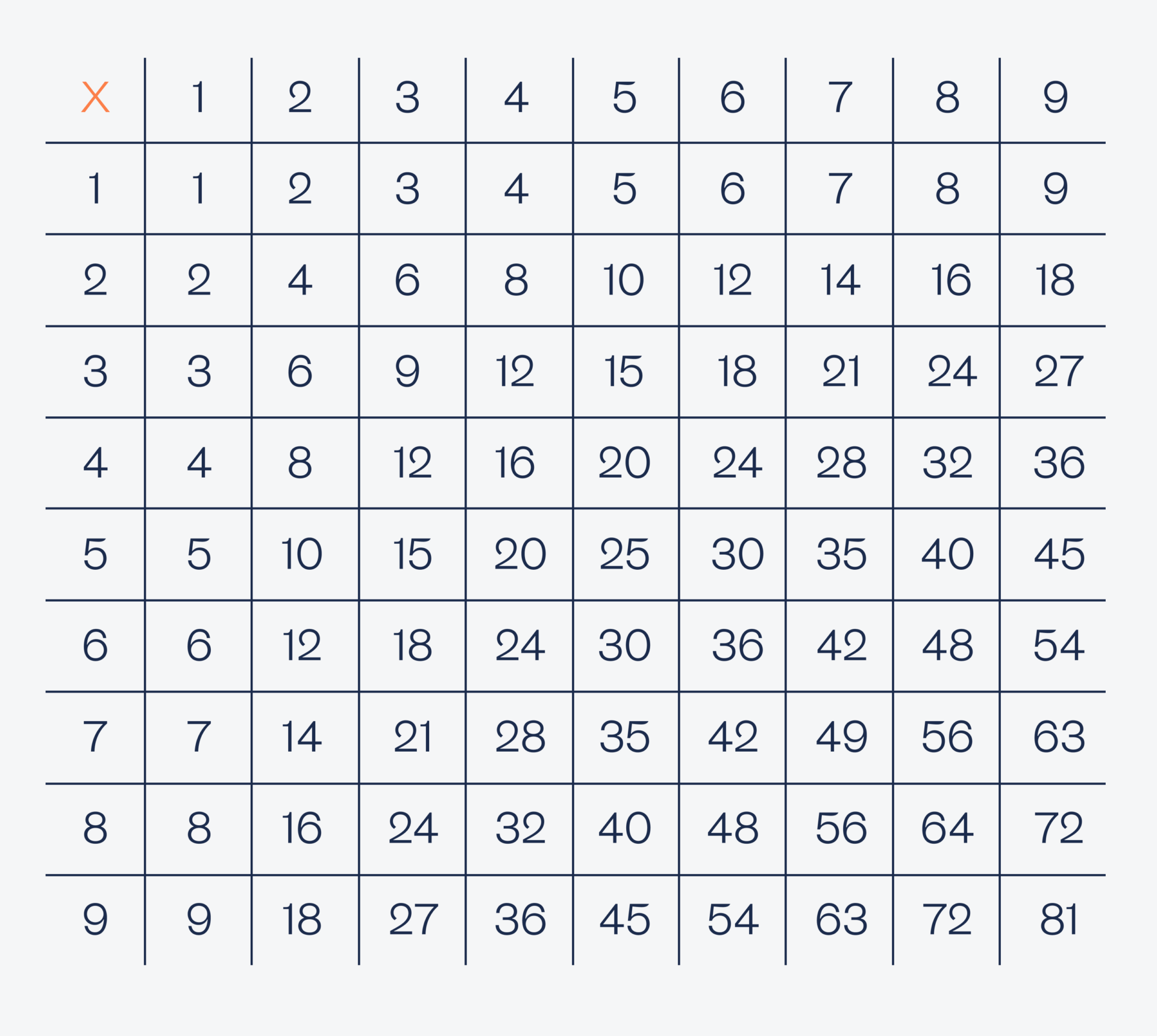
Раз нам всё равно, в каком порядке первый программист загадал свои числа, а важен только результат умножения, то мы отбросим половину значений — а всё потому, что 2 × 6 = 6 × 2. Поэтому убираем нижнюю половину таблицы — она дублирует верхние значения:
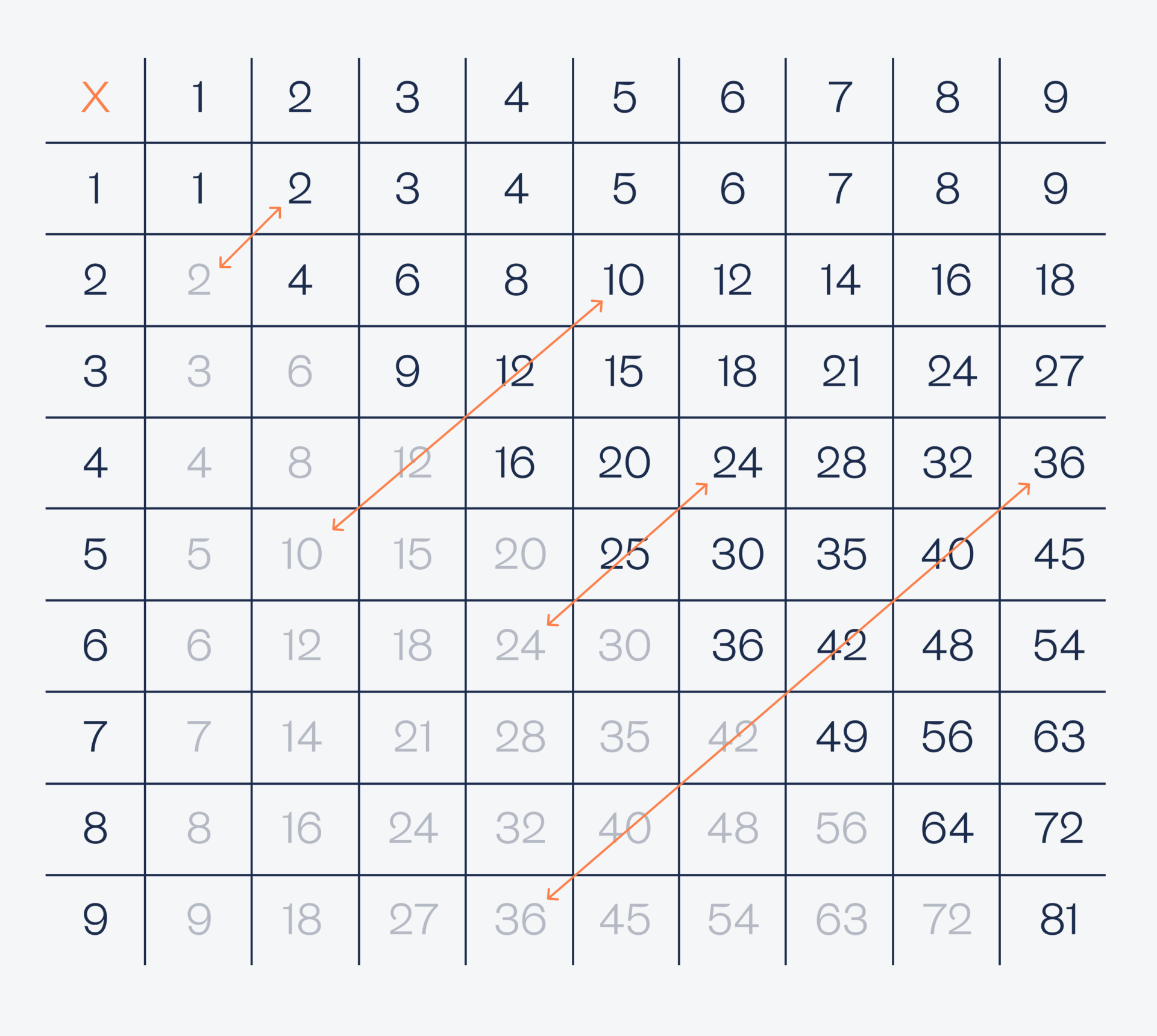
В условии сказано, что первый программист загадал разные числа, поэтому диагональ с результатами тоже можно отбросить — там результат умножения одинаковых чисел:
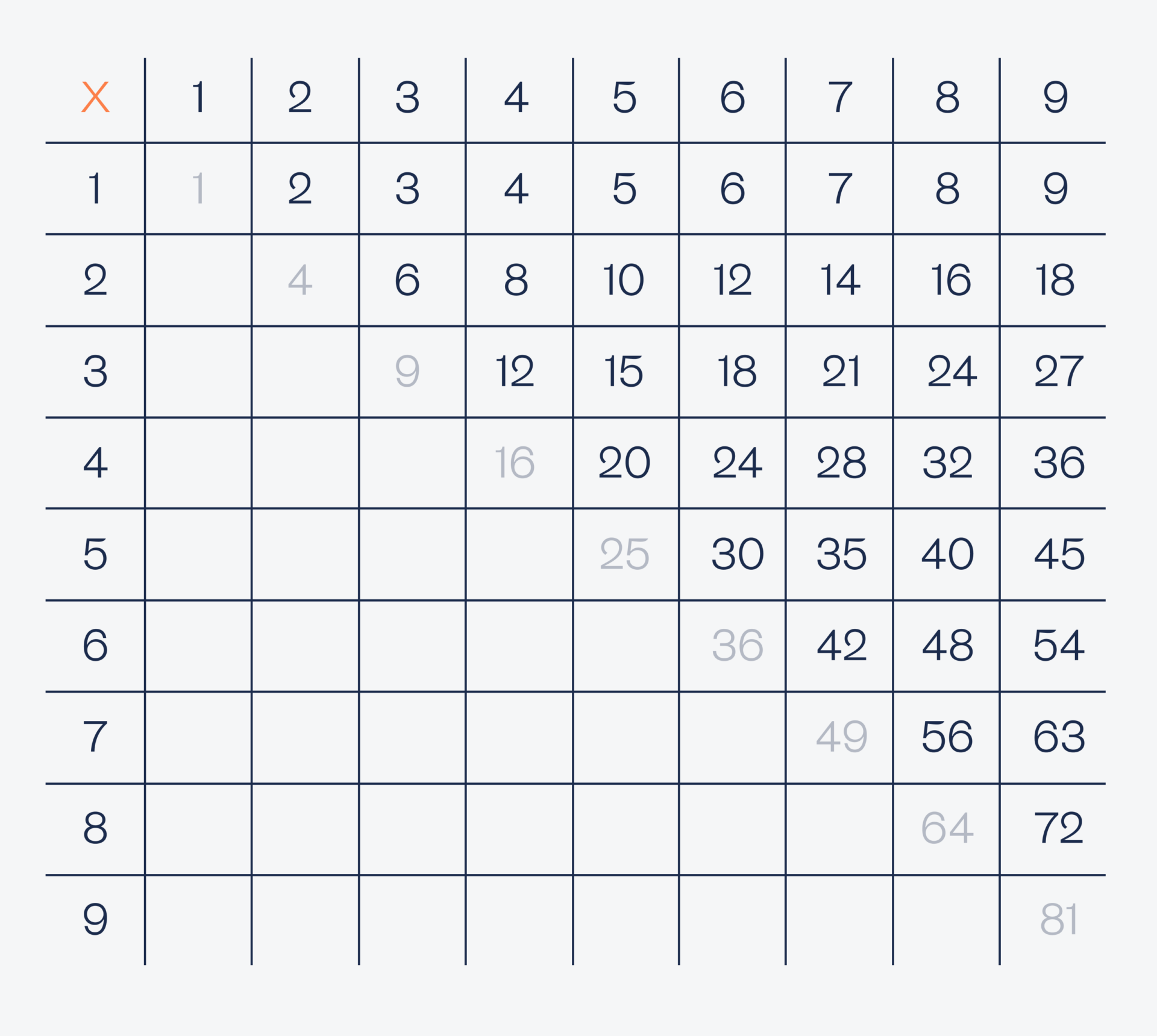
Так как последняя цифра в результате произведения совпадает с номером дома первого программиста, можно сделать вывод, что номер дома — однозначное число от 1 до 9 (потому что нумерация домов начинается с единицы, а не с нуля).
Теперь самая нудная часть решения: нам нужно по очереди сравнить все числа от 1 до 9 с последними цифрами произведений, и если таких результатов будет больше одного — отбросить их. Дело в том, что второй программист сразу понял ответ, а это можно сделать, только когда вариантов решения не больше одного.
Для примера подробно разберём число 1: находим все результаты произведений, которые заканчиваются на единицу:
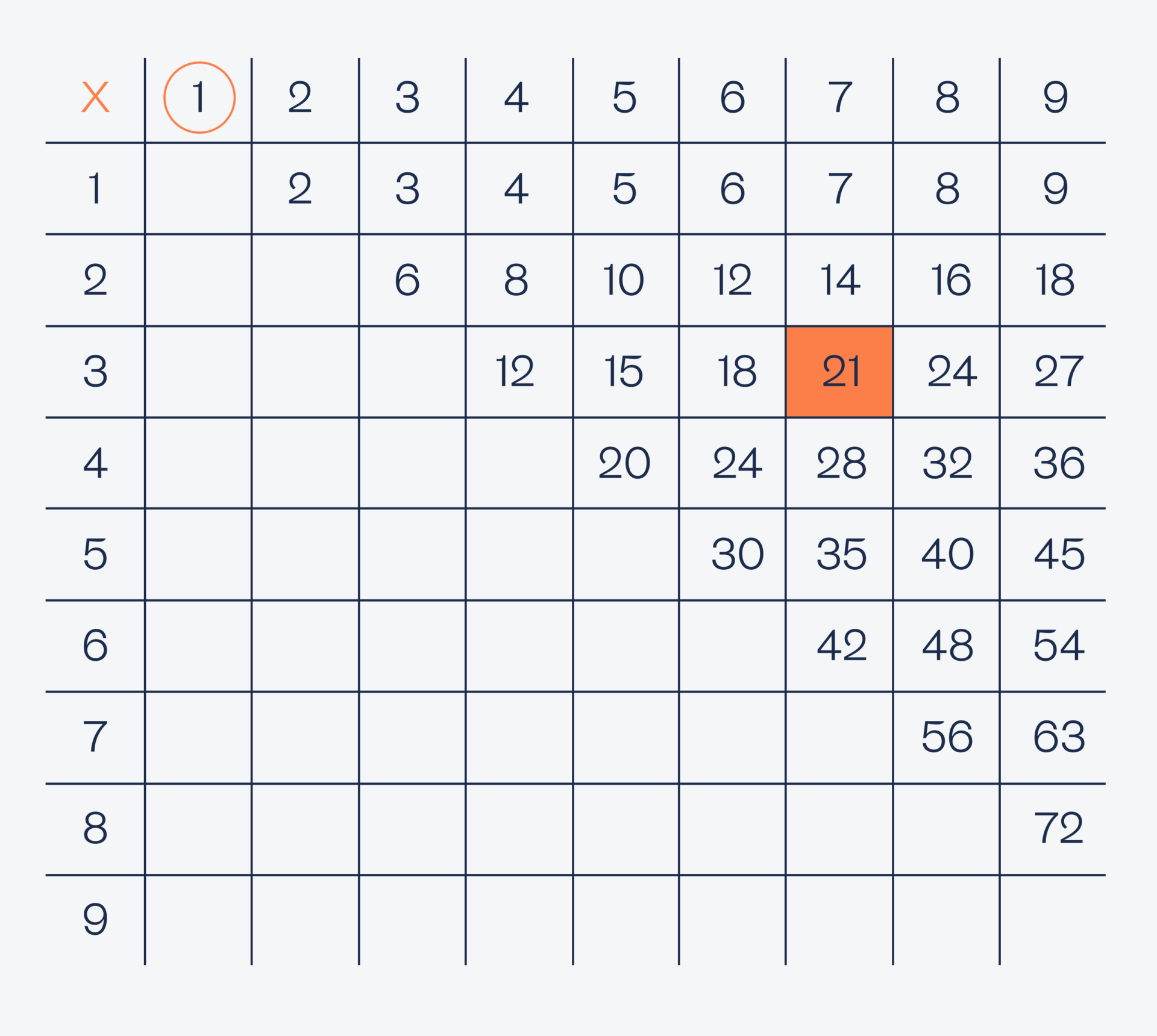
Такой результат у нас только один — это число 21. Кажется, что мы сразу нашли верный ответ, но вдруг нет? Нужно точно так же проверить все остальные числа — возможно, будет ещё такое уникальное произведение.
Проверяем двойку:
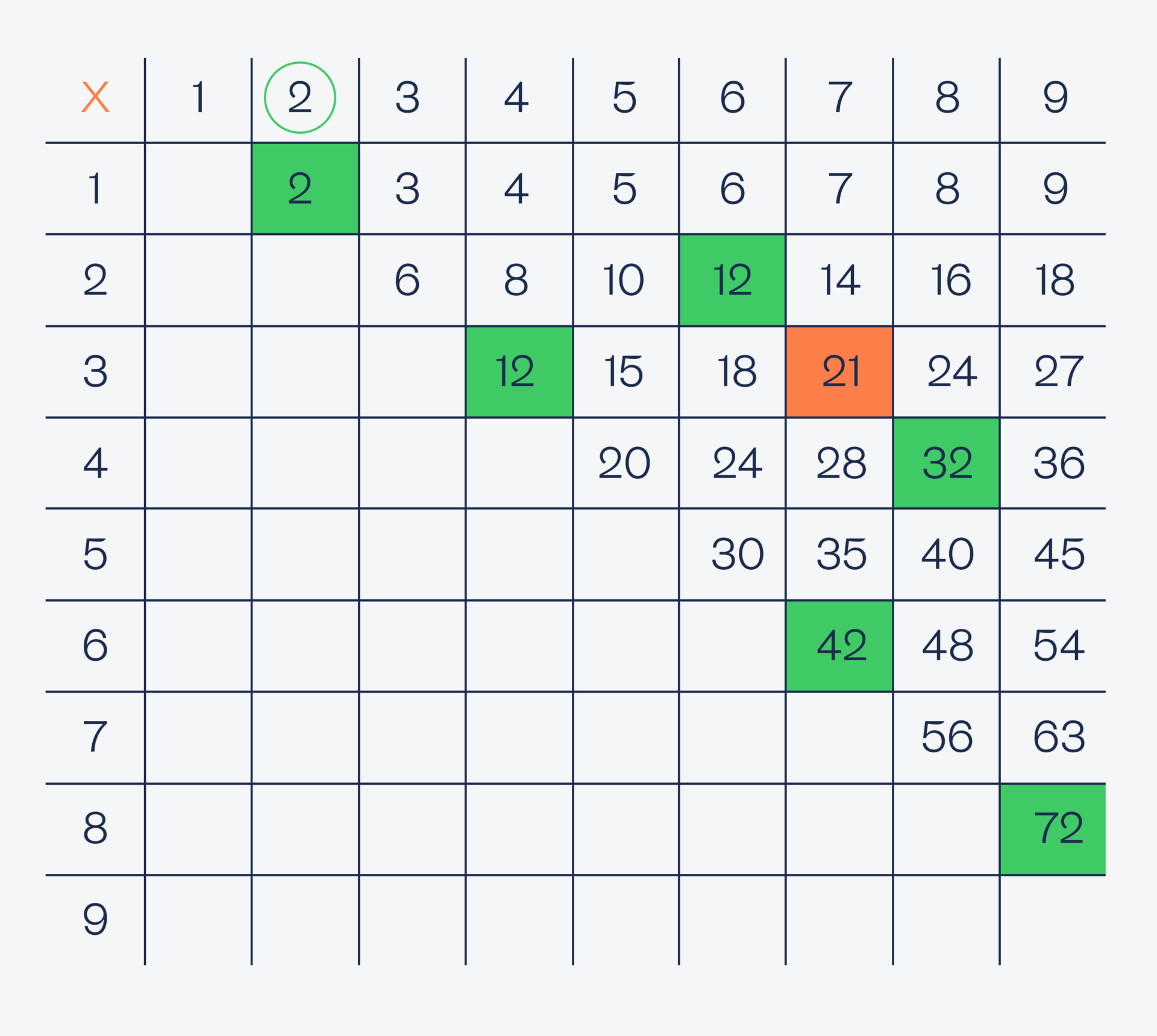
А здесь у нас получилось сразу много произведений с двойкой на конце, поэтому все эти результаты можно отбрасывать как неверные (они не дают однозначного ответа). Точно так же проверим всё остальное и вычеркнем неоднозначные результаты.
Проверяем тройку:
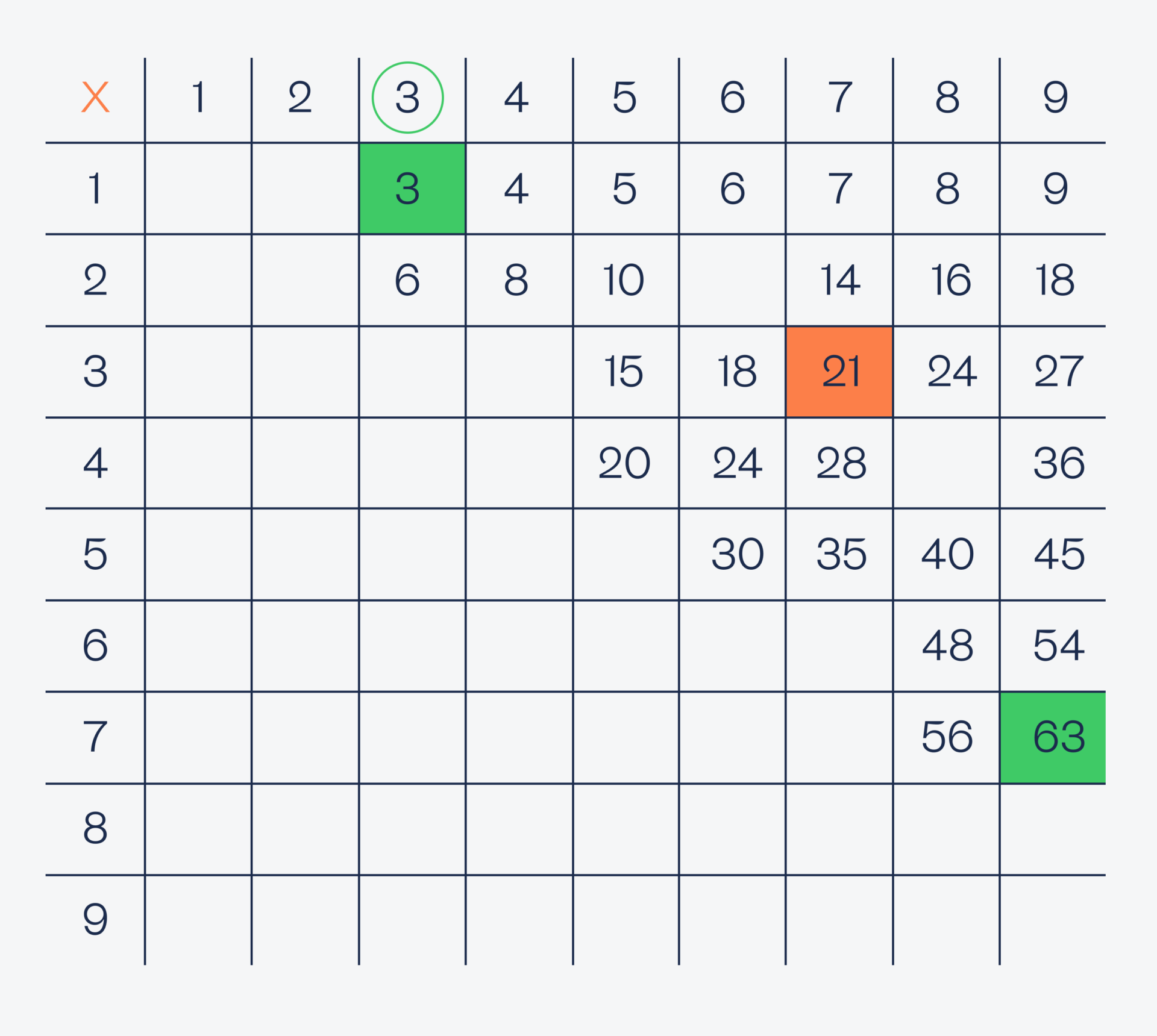
Проверяем четвёрку:
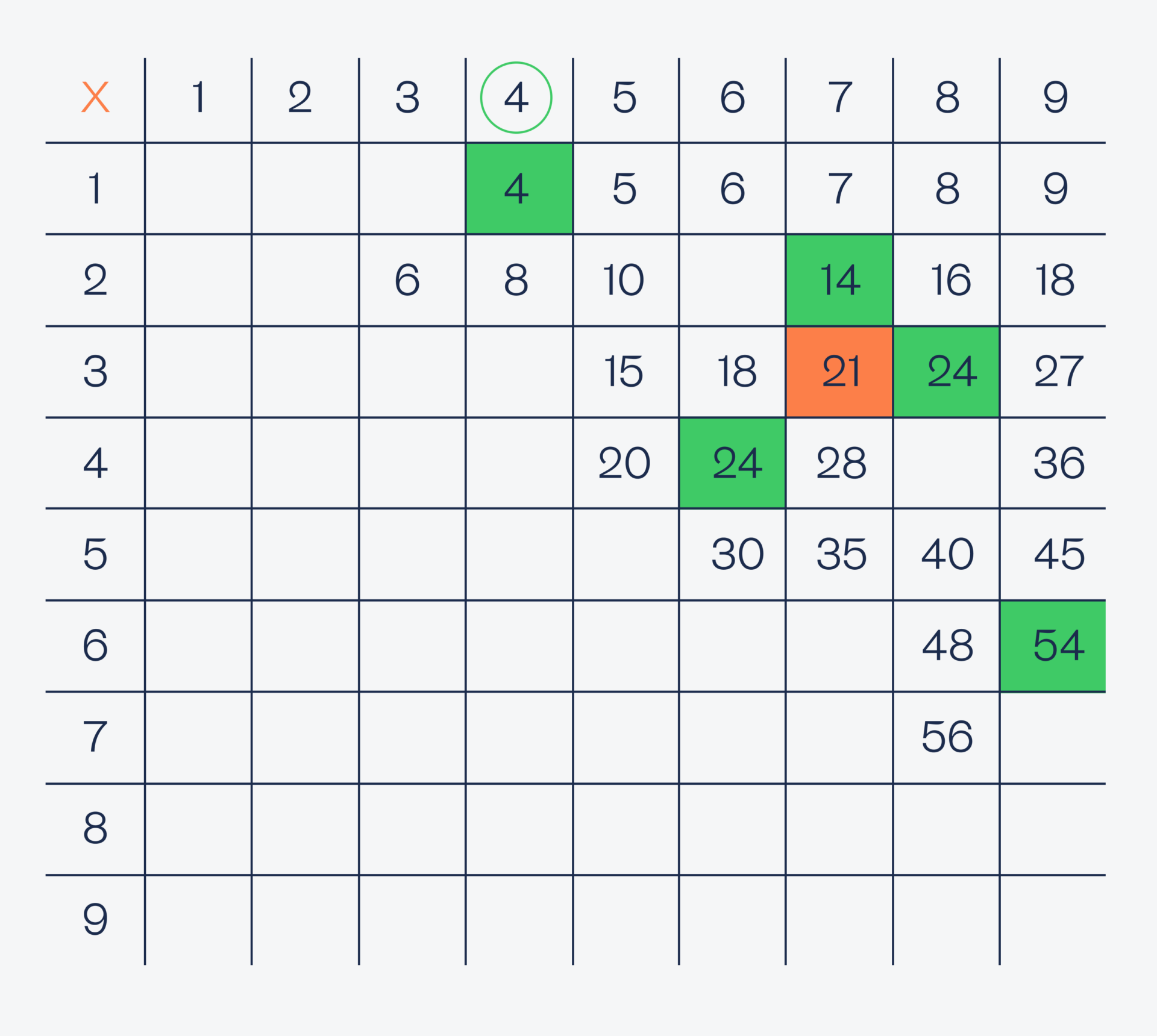
Проверяем пятёрку:
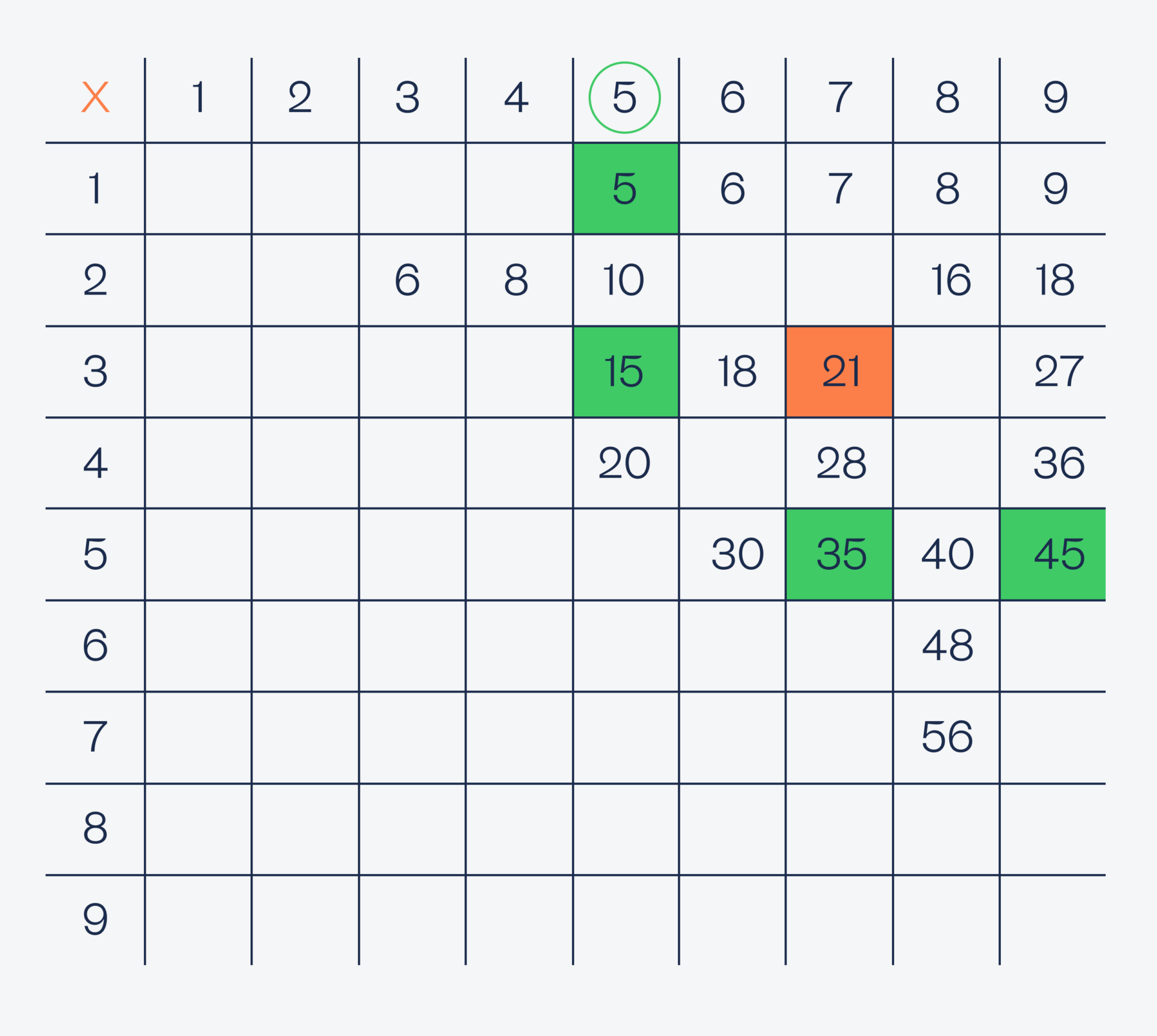
Проверяем шестёрку:
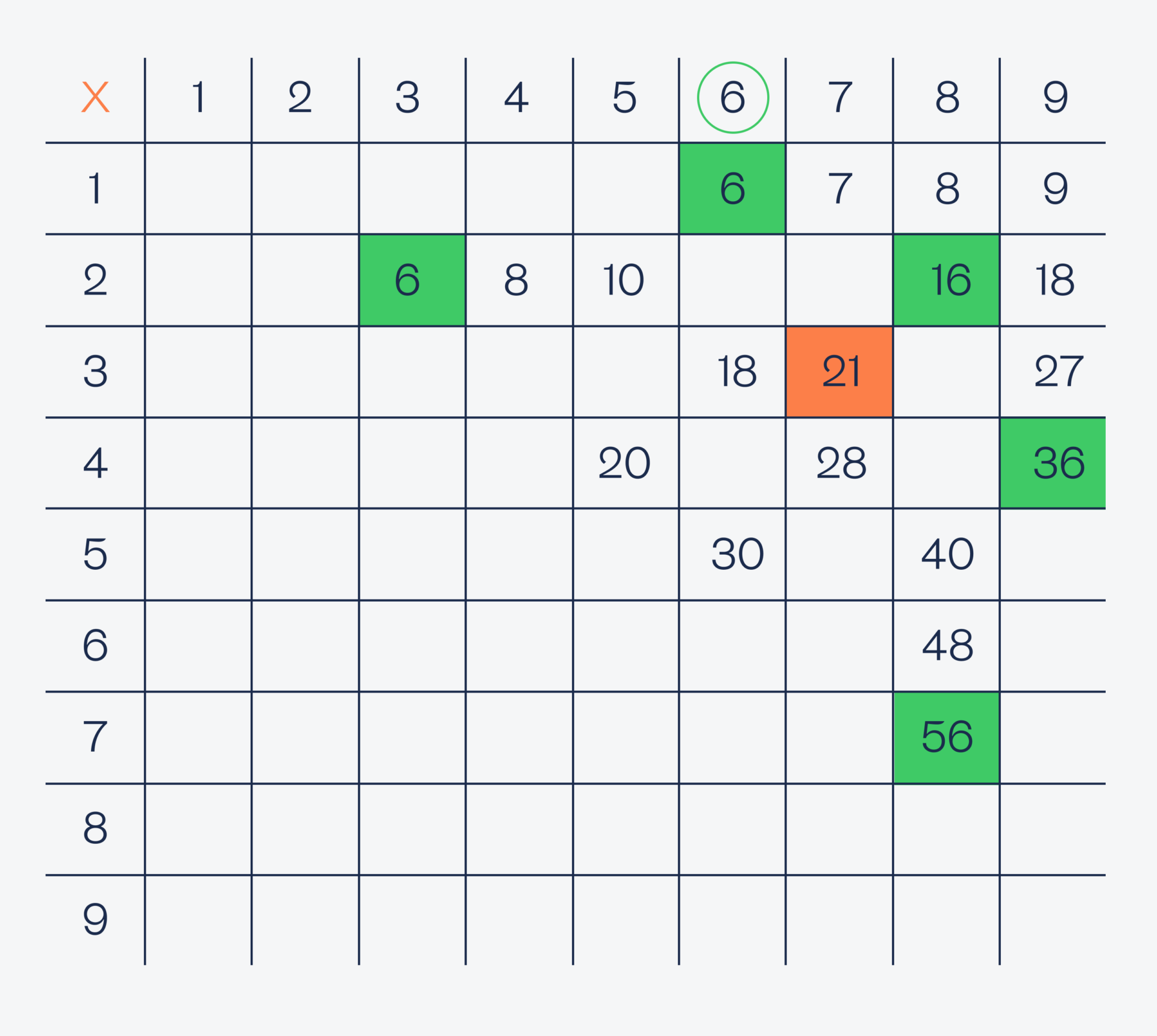
Проверяем семёрку:
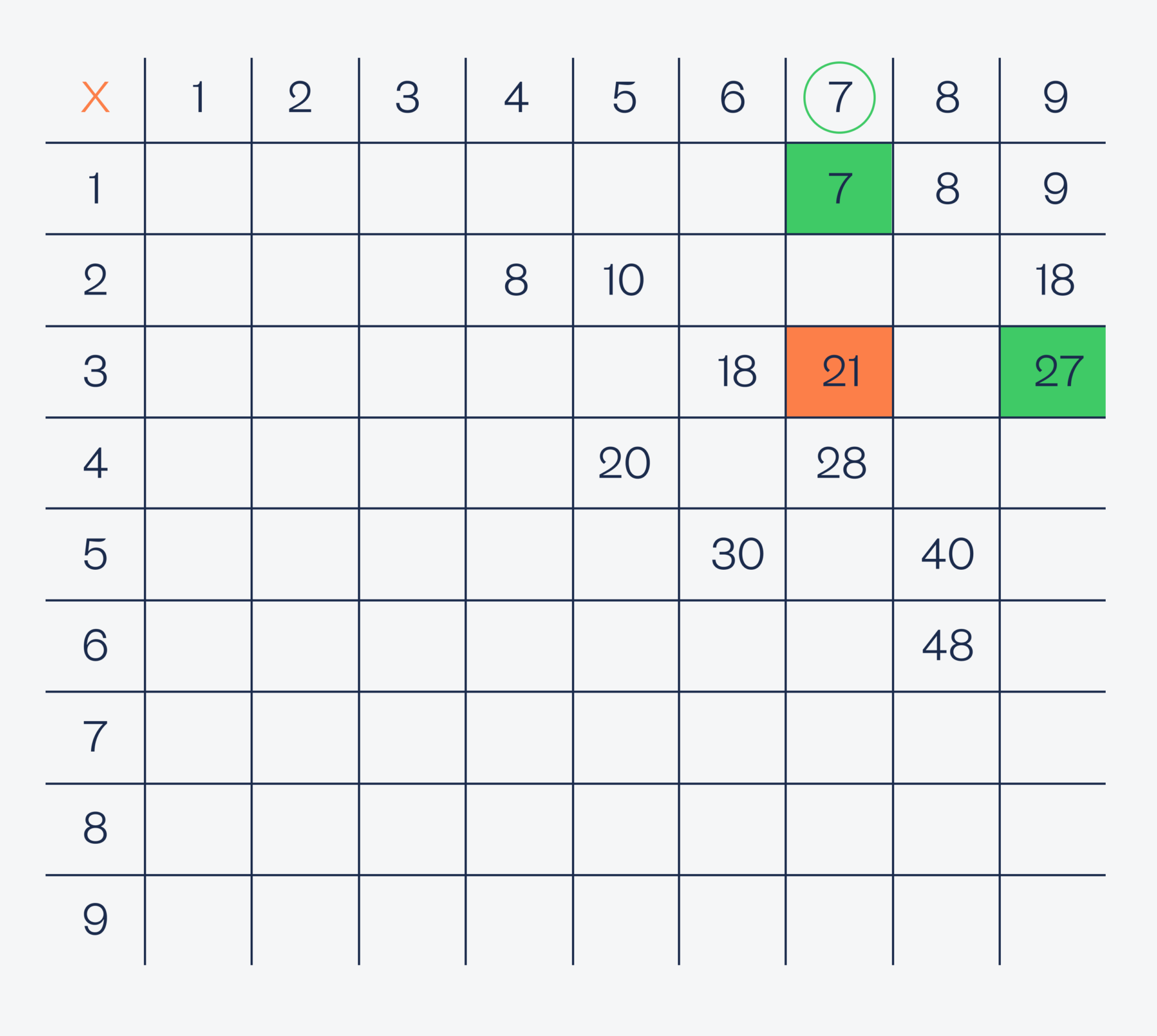
Проверяем восьмёрку:
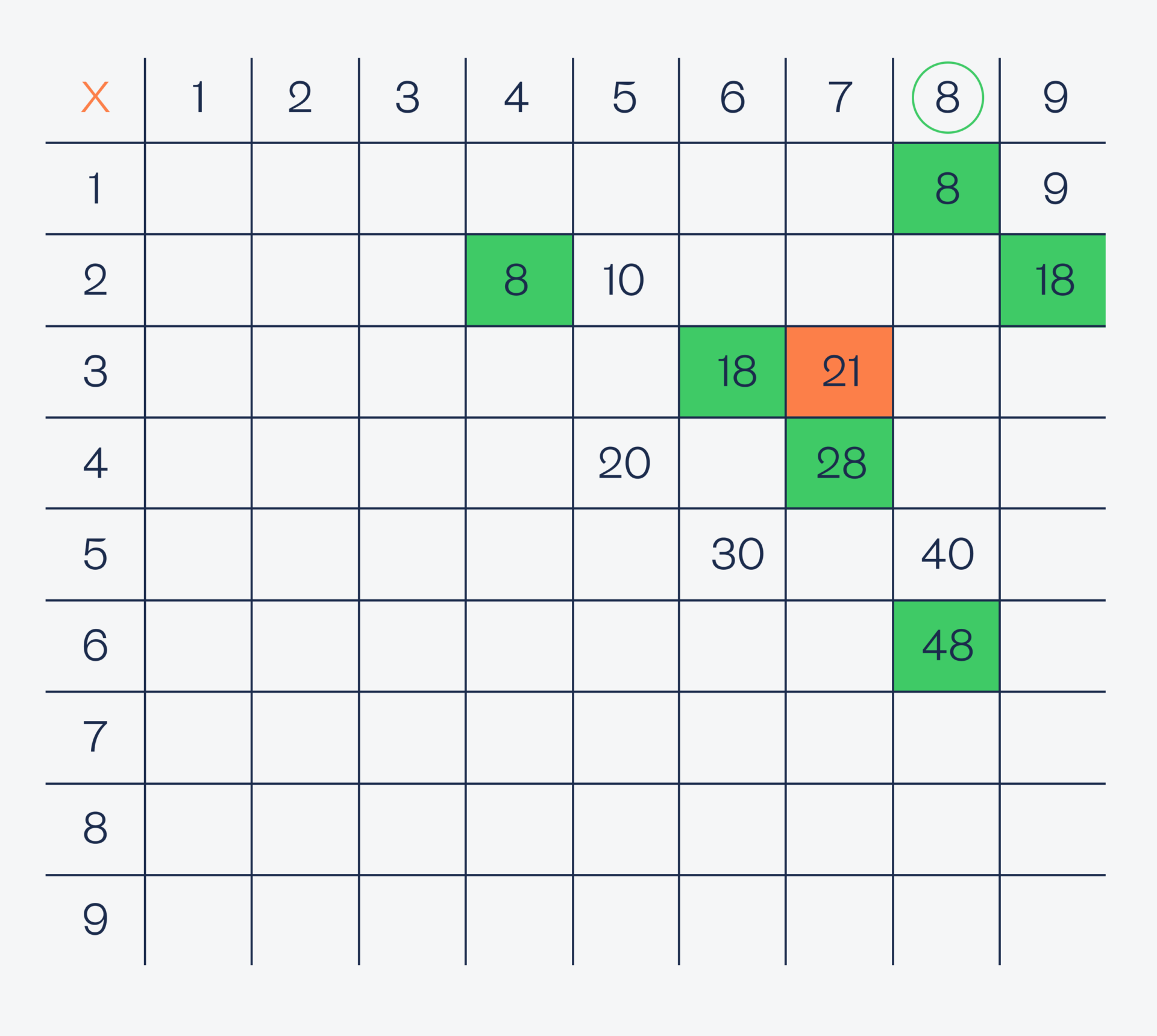
Проверяем девятку: у неё тоже один результат, поэтому тоже оставляем его как один возможных.
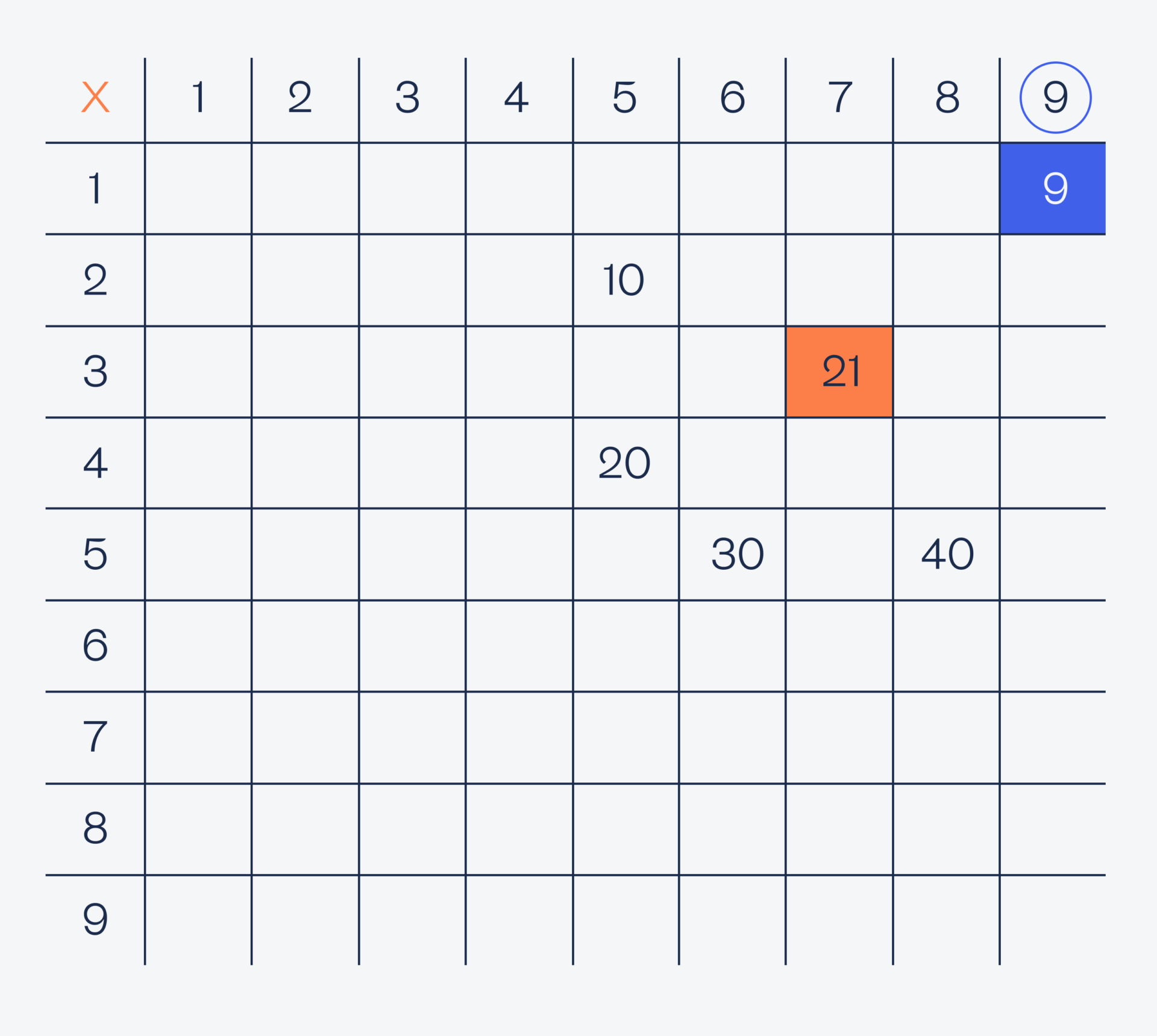
А всё, что заканчивается на ноль, тоже убираем — у нас нет ноля среди загаданных чисел:
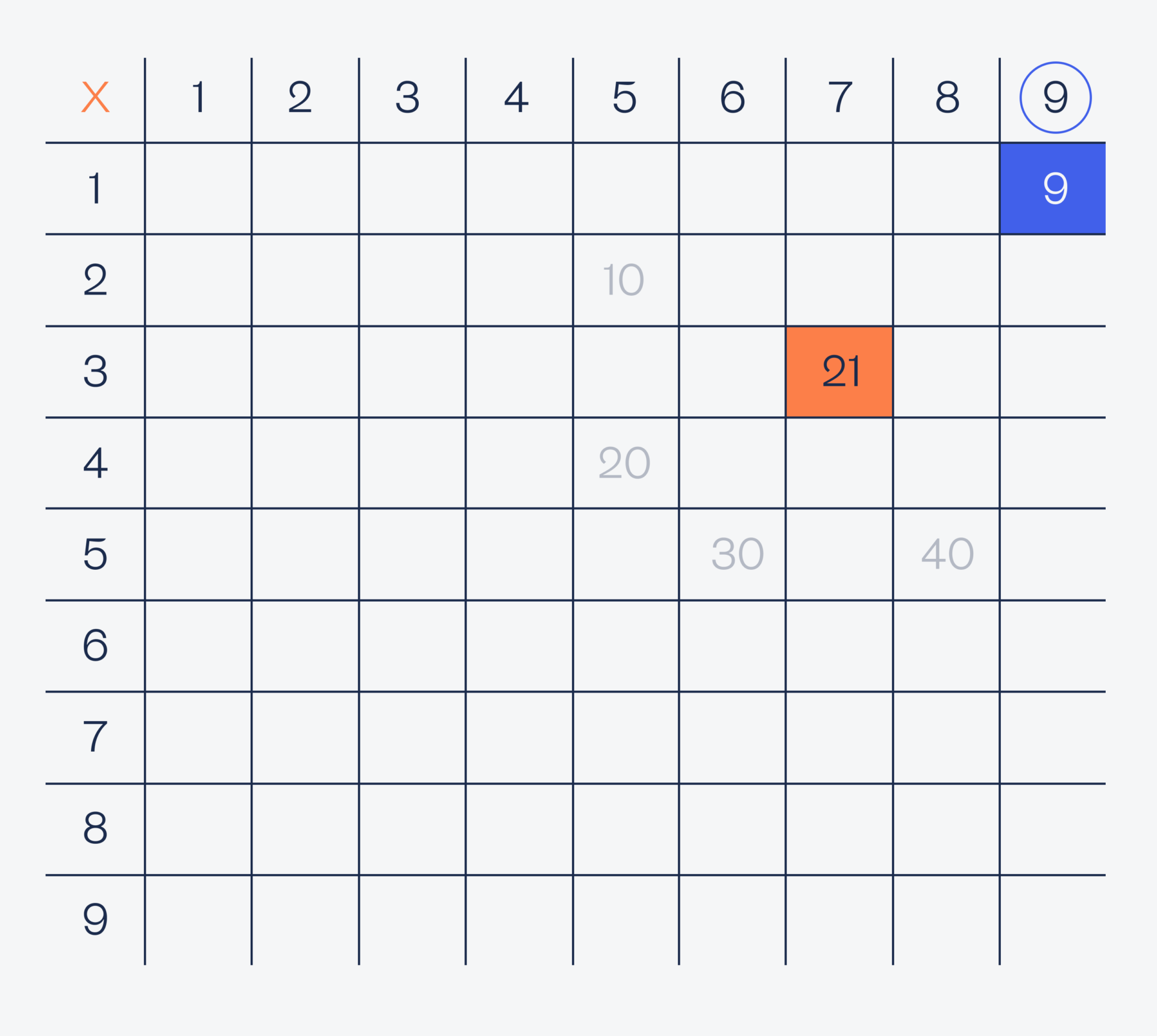
Итак, у нас остались всего два числа: 9 и 21, и по идее нам нужно как-то выбрать одно из них, чтобы найти исходную пару чисел и выяснить их сумму. Но давайте посмотрим на то, произведение каких чисел даёт эти результаты:
1 × 9 = 9
3 × 7 = 21
А теперь попробуем сложить эти числа:
1 + 9 = 10
3 + 7 = 10
И там и там сумма равна 10, а значит, мы можем дать правильный ответ в любом случае: сумма загаданных чисел равна 10.
Логическая задача про странные часы
Есть обычные настенные часы, но без цифр и без указания, где у них верх, а где низ. Все стрелки на часах одинаковые — секундная, минутная и часовая.
Задача — по одному изображению этих часов определить, какое время они показывают.
Подсказки:
- Все стрелки двигаются плавно.
- Циферблат не отзеркален.
- Крупные риски показывают часы или пятиминутные отрезки.
- Решение задачи опирается на то, как работают часы.
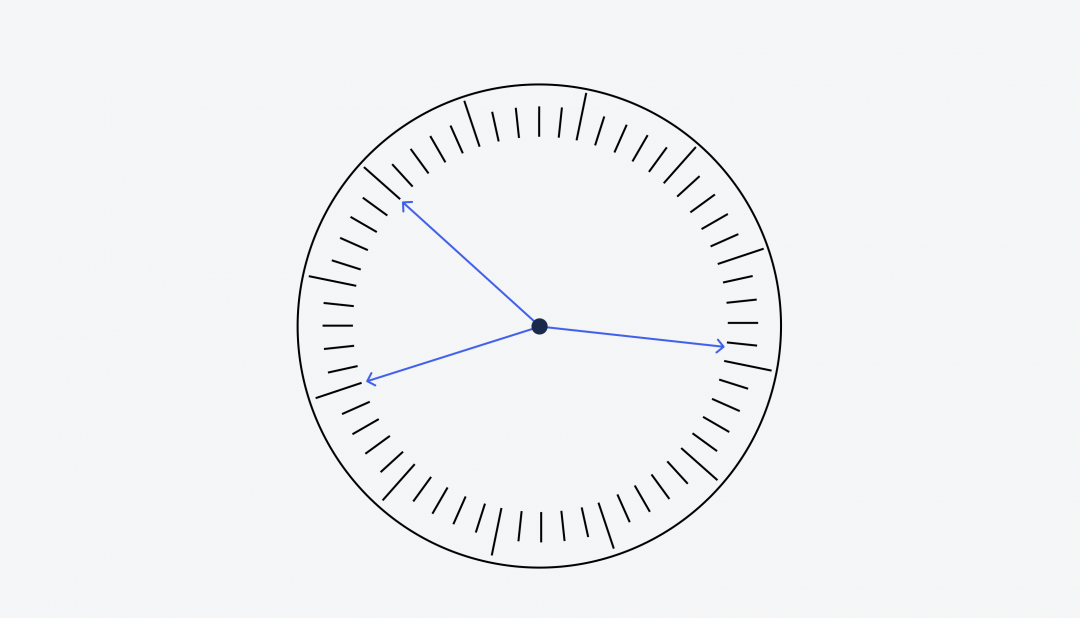
Чтобы как-то отличать стрелки друг от друга, мы их подпишем — A, B и C:
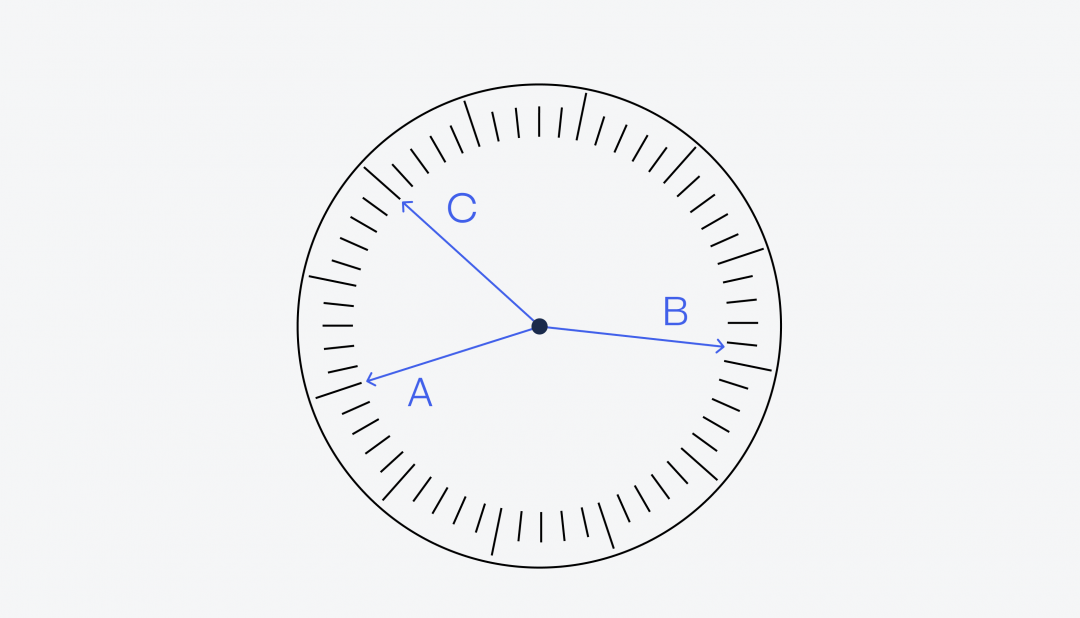
Теперь будем делать разные предположения, какая стрелка за что отвечает, а потом посмотрим, к чему это приведёт. Это, кстати, один из вариантов решения любых сложных задач: сформулировать какую-то гипотезу, принять её за правильный ответ и посмотреть, а бьётся ли задача с этим предположением.
Гипотеза: часовая стрелка — A или C. Стрелки A и C указывают точно на часовые (или пятиминутные) отметки. Если бы одна из этих стрелок была часовой (показывала часы), то обе оставшихся стрелки указывали бы ровно на отметку в 12 часов. А всё потому, что часовая стрелка указывает точно на свой час только в тот момент, когда минутная и секундная указывают на 12.
Раз у нас ни одна стрелка не совпадает по расположению с другой, значит наша гипотеза неверна и ни A, ни C — не часовые стрелки. А раз так, значит, остаётся единственная часовая стрелка — это B.
Вывод: B — часовая стрелка.
Раз обе эти стрелки указывают точно на часовые отметки, значит, секундная направлена точно на 12 часов, а минутная — на какую-то только что наступившую минуту.
Теперь получается два варианта:
- A — секундная, C — минутная стрелка.
- С — секундная, А — минутная стрелка.
Возьмём первый вариант как новую рабочую гипотезу (A — секундная, C — минутная). Раз A — секундная и показывает точно на 12, то мы можем оттолкнуться от этого и пронумеровать все остальные деления на часах:
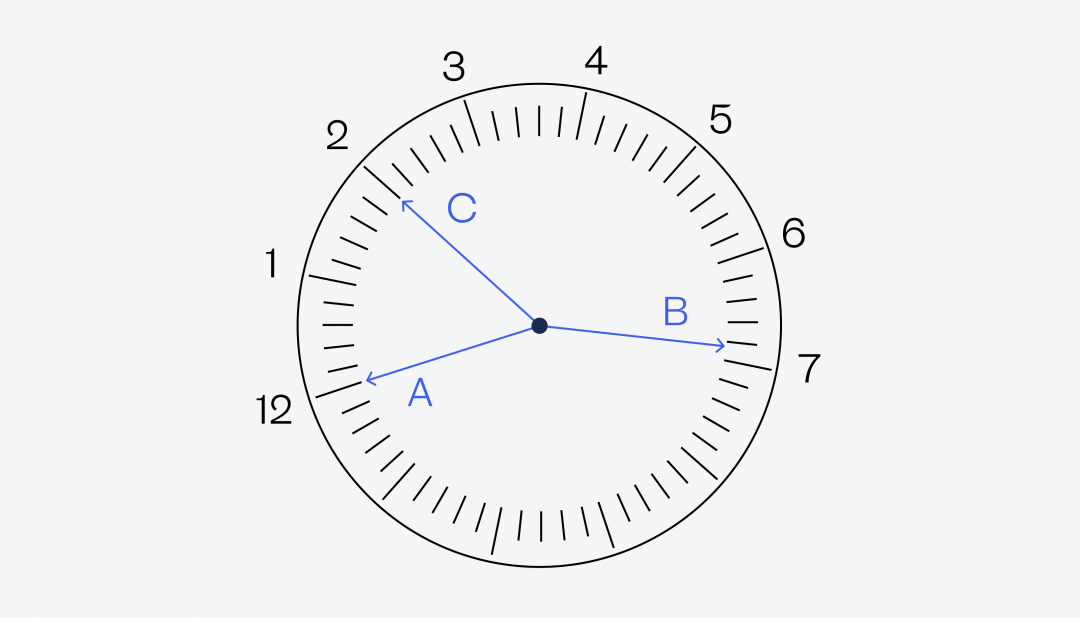
Но раз так, то минутная (C) показывает, что прошло 10 минут с начала часа, а часовая (B) — что час вот-вот закончится. Так не бывает в нормальных часах, поэтому этот вариант мы отбрасываем.
Новая гипотеза: С — секундная, А — минутная стрелка. Рассмотрим второй вариант, когда секундная стрелка — это С, и она указывает точно на 12. Отталкиваясь от этого, пронумеруем остальной циферблат и посмотрим, что получилось:
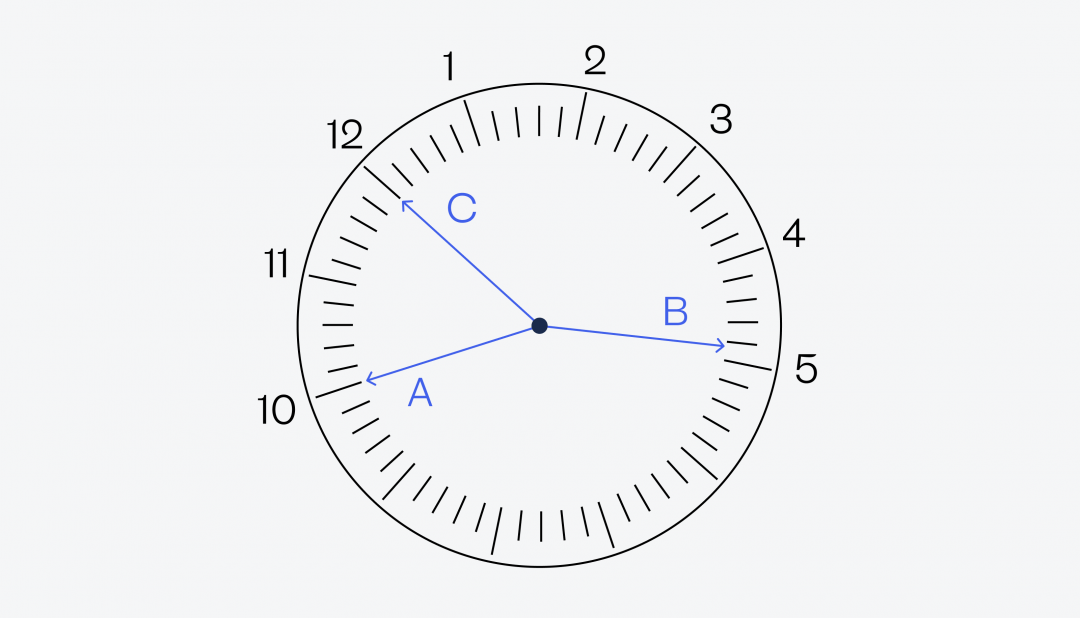
Минутная стрелка у нас указывает теперь на 10 — это значит, что до конца часа осталось 10 минут. Посмотрим на часовую стрелку: она почти дошла до пятёрки, а значит, до конца часа осталось совсем немного, например те же 10 минут. Кажется, мы нашли правильный ответ. Чтобы в этом убедиться, перевернём циферблат правильно:
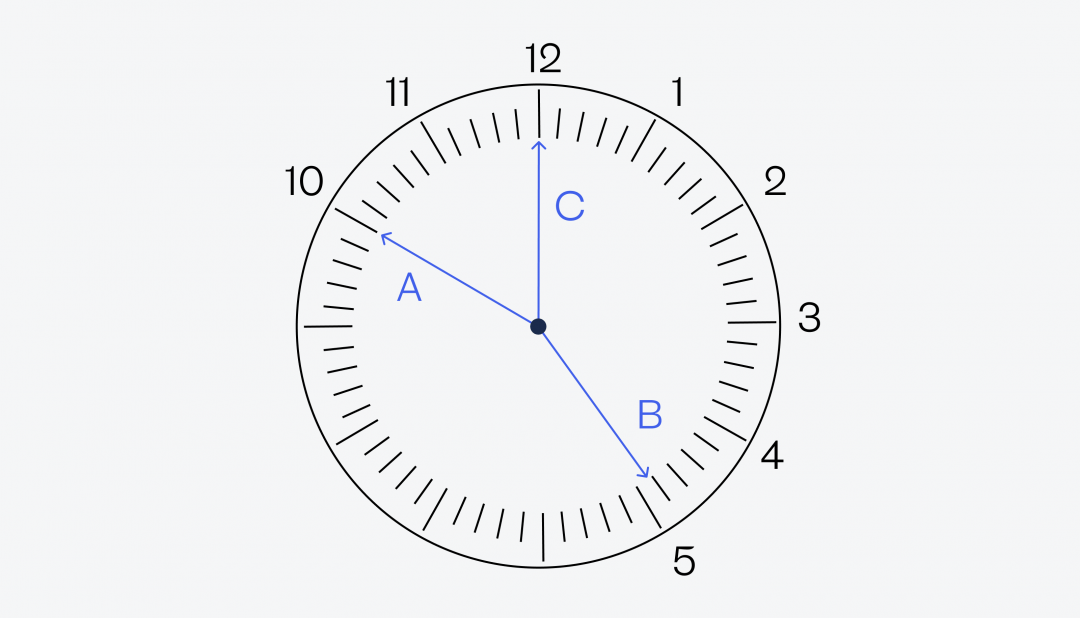
Получается, что часы показывают 4:50 или 16:50.