В давние времена, когда «Амазон» не увольнял, а набирал сотрудников, там давали такую задачку:
Есть пять цифр: 1, 2, 3, 4, 5. С помощью перестановок из них составили все возможные комбинации пятизначных чисел. Найдите сумму этих чисел как можно быстрее.
Решать можно как угодно, оценивается сам ход решения.
Самый простой способ решения выглядит так:
- Берём листочек и выписываем все варианты перестановок.
- Запускаем калькулятор и начинаем складывать по очереди все числа.
- Так делаем 120 раз.
- Profit!
Проблема в том, что нам нужно найти решение как можно быстрее, а выписывать и потом складывать 120 чисел — долго. Дело в том, что общее количество перестановок без повторений из пяти элементов — это 5!, то есть факториал пяти:
5! = 1 × 2 × 3 × 4 × 5
Ещё можно ошибиться в одной из комбинаций и из-за этого получить неправильный ответ. Так что это точно не самый быстрый способ решения задачи.
Если у нас есть под рукой браузер и пять свободных минут, можно написать код, который простым перебором найдёт все комбинации и посчитает их сумму. Логика кода будет такая:
- Пишем функцию, которая сгенерирует все перестановки.
- Запускаем её и все перестановки сохраняем в отдельную переменную.
- В этой переменной каждая перестановка хранится в виде отдельного мини-массива
- В первом цикле перебираем основной массив со всеми вариантами.
- Во вложенном цикле перебираем все 5 знаков числа, умножаем их на соответствующую степень десятки и прибавляем к результату.
- Когда все циклы закончились — выводим результат.
На всё это пяти минут хватит с запасом, если писать код без комментариев. Раз у нас под рукой только браузер, напишем код на JavaScript. Запускаем код и видим в консоли ответ:
3 999 960
Вручную такое мы бы точно считали очень долго.
👉 Спасательный круг для тех, кто начинает писать на JavaScript
// функция для получения всех перестановок
const permutator = (inputArr) => {
// итоговый массив
let result = [];
// создаём вложенную функцию
const permute = (arr, m = []) => {
// если в массиве не осталось элементов
if (arr.length === 0) {
// добавляем новый элемент в промежуточный массив
result.push(m)
// в ином случае
} else {
// перебираем все элементы массива
for (let i = 0; i < arr.length; i++) {
// получаем начало очередной комбинации
let curr = arr.slice();
// сдвигаем на единицу и формируем окончание
let next = curr.splice(i, 1);
// рекурсивно обрабатываем вторую часть массива
permute(curr.slice(), m.concat(next))
}
}
}
// переставляем элементы массива
permute(inputArr)
// возвращаем результат
return result;
}
// сумма всех чисел-перестановок
var sum = 0;
// получаем все перестановки из пяти чисел
var a = permutator([1,2,3,4,5]);
// перебираем все 120 комбинаций
for (let i = 0; i < 120; i++){
// в каждой перебираем все 5 внутренних цифр
for (let j = 0; j < 5; j++){
// добавляем к сумме текущее пятизначное число
sum += a[i][j]*Math.pow(10,j);
}
}
// выводим результат
console.log(sum);Это решение может оказаться быстрее предыдущего, потому что нам не нужно будет тестировать код и перепроверять логику его работы. Вместо кода мы сделаем такую хитрость:
- Поставим на первое место цифру 5.
- Раз 5 стоит на первом месте в пятизначном числе, значит, она отвечает за десятки тысяч, поэтому умножим её на 10⁴ — 5(10⁴)
- Теперь посмотрим, сколько комбинаций у нас получится с пятёркой на первом месте

Применим ту же формулу нахождения количества перестановок, что и в первом решении — для 4 цифр количество вариантов равно 4! Если мы учтём, что пятёрка стоит на первом месте в числе, получится такое:
5(10⁴) × 4! — это общая сумма пятёрок во всех комбинациях, если она стоит на первом месте.
Точно так же посчитаем сумму всех пятёрок, если они будут стоять на втором месте, то есть на месте тысяч:

Количество перестановок останется таким же, только поменяется степень десятки — теперь цифра 5 отвечает за тысячи:
5(10³) × 4! — это общая сумма пятёрок во всех комбинациях, если она стоит на втором месте.
Таким же способом находим общие суммы пятёрок на остальных местах:
5(10²) × 4! — общая сумма пятёрок на третьем месте (сотни)
5(10¹) × 4! — на четвёртом месте (десятки)
5(10⁰) × 4! — на пятом месте (единицы)
Итого, если найти сумму всех пятёрок во всех комбинациях на разных местах, у нас выйдет такое:
5(10⁴) × 4 + 5(10³) × 4! + 5(10²) × 4! + 5(10¹) × 4! + 5(10⁰) × 4!
Вынесем общие множители за скобки:
5 × (10⁴ + 10³ + 10² +10¹ + 10⁰) × 4!
Получается, единственное, что влияет на общую сумму в случае одного числа — это оно само в виде первого множителя. По аналогии найдём суммы остальных чисел на разных позициях:
4 × (10⁴ + 10³ + 10² +10¹ + 10⁰) × 4!
3 × (10⁴ + 10³ + 10² +10¹ + 10⁰) × 4!
2 × (10⁴ + 10³ + 10² +10¹ + 10⁰) × 4!
1× (10⁴ + 10³ + 10² +10¹ + 10⁰) × 4!
Наконец, чтобы найти общую сумму всех комбинаций и чисел в них, сложим все промежуточные варианты. Сразу вынесем за скобку общий множитель:
(5 + 4 + 3 + 2 + 1) × (10⁴ + 10³ + 10² +10¹ + 10⁰) × 4!
15 × (1000 + 1000 + 100 +10 + 1) × 4!
15 × 1111 × 4!
15 × 1111 × 24 ← такое можно легко посчитать на листочке или калькуляторе
Перемножив числа, получим тот же ответ, что и с кодом — 3 999 960
Внешне решение выглядит громоздко, но если вы попробуете выписать его на листочке, то удивитесь, насколько быстро получается готовый ответ.
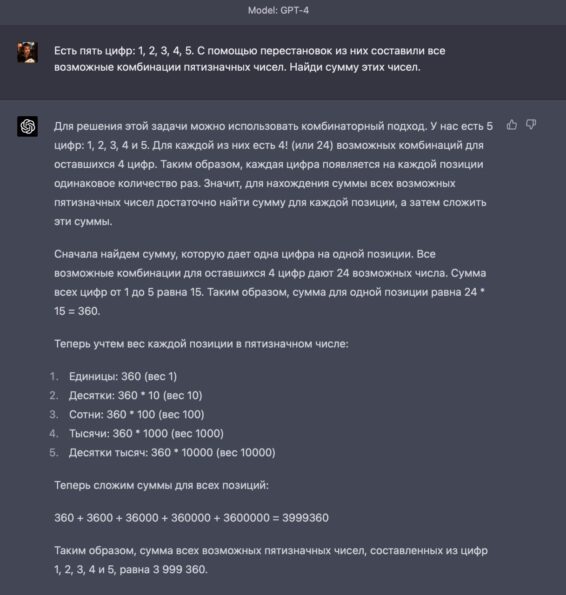
Запрос: Есть пять цифр: 1, 2, 3, 4, 5. С помощью перестановок из них составили все возможные комбинации пятизначных чисел. Найди сумму этих чисел. Прокомментируй решение.
Ответ модели ChatGPT 3.5:
Чтобы найти сумму всех возможных комбинаций пятизначных чисел из пяти данных цифр, нужно сначала определить, сколько раз каждая цифра может стоять на каждой позиции в числе. Так как мы имеем дело с пятизначными числами, каждая цифра может стоять на каждой из пяти позиций, т. е. по пять раз. Таким образом, каждая цифра будет встречаться 5! = 120 раз во всех возможных комбинациях.
Для нахождения суммы всех чисел можно использовать следующий алгоритм:
- Найдём сумму цифр, умноженных на 11111 (это число, составленное из пяти единиц).
- Умножим эту сумму на 120 (количество комбинаций).
- Результатом будет сумма всех возможных комбинаций.
Таким образом:
Сумма цифр, умноженных на 11111 = 1*11111 + 2*11111 + 3*11111 + 4*11111 + 5*11111 = 123455
Сумма всех возможных комбинаций = 123455 * 120 = 14,814,600
Ответ: 14,814,600.
Примечание редакции: пока что не смог.