Бабушка собрала большой урожай трёх сортов яблок — антоновки, белого налива и грушовки. В каждой корзине лежали яблоки только одного сорта:
- в первой корзине — 20 яблок;
- во второй — 24;
- в третьей — 28;
- в четвертой — 32;
- в пятой — 36;
- в шестой — 40;
- в седьмой — 44;
- в восьмой — 48.
После того как бабушка продала программисту целую корзину грушовки, она сказала, что грушовки осталось в два раза больше, чем антоновки, и в два раза меньше, чем белого налива. Программист услышал это, спросил, сколько яблок было в каждой корзине, и сразу сказал, в каких корзинах у бабушки лежала антоновка, а в каких — грушовка.
Как он это сделал?
Эту задачу можно решить двумя способами — логически и грубой силой на Python. Сначала попробуем логически.
Обозначим за Х количество антоновки, которое осталось после продажи одной корзины грушовки. Тогда грушовки осталось 2Х, а белого налива — 4Х, потому что его было в два раза больше, чем грушовки. Итого — Х + 2Х + 4Х = 7Х яблок.
Раз перед иксом стоит множитель 7, то это значит, что итоговая сумма должна быть кратна 7, то есть делиться на семь без остатка. Первоначальное количество яблок — 272 штуки, и если разделить 272 на 7, получим в остатке 6. Но оставшиеся яблоки делятся на 7 нацело, и это значит, что как раз проданная корзина даёт в остатке 6. Таких корзин у бабушки было две: та, где 20 яблок, и та, где 48. Проверим оба варианта.
Продали корзину с 20 яблоками
Если программист купил первую корзину грушовки с 20 яблоками, то всего яблок осталось 252, а значит, антоновки осталось 252 / 7 = 36 штук. Это значит, что она вся лежит сейчас в 5-й корзине.
Если грушовки осталось в 2 раза больше, значит её — 36 × 2 = 72 штуки. Раз у нас нет корзины, где лежит сразу 72 яблока, значит, это количество наберётся в двух или трёх корзинах. Попробуем их найти.
Вариант 1: корзина с 24 яблоками (вторая) + что-то ещё. Раз у нас 72 яблока, а в одной корзине их 24, то где-то ещё лежит 72 − 24 = 48 яблок — а это как раз восьмая корзина.
Вариант 2: корзина с 28 яблоками (третья) + что-то ещё. Раз у нас 72 яблока, а в одной корзине их 28, то где-то ещё лежит 72 − 24 = 44 яблок — а это как раз седьмая корзина.
Вариант 3: корзина с 32 яблоками (четвёртая) + что-то ещё. Раз у нас 72 яблока, а в одной корзине их 32, то где-то ещё лежит 72 − 32 = 40 яблок — а это как раз шестая корзина.
Вариант 4: корзина с 36 яблоками (пятая) + что-то ещё. Раз у нас 72 яблока, а в одной корзине их 36, то где-то ещё лежит 72 − 36 = 36 яблок — такой корзины у бабули нет, поэтому такой вариант нам не подходит.
Вариант 5: корзина с 40 яблоками (шестая) + что-то ещё. Раз у нас 72 яблока, а в одной корзине их 40, то где-то ещё лежит 72 − 40 = 32 яблока — а это как раз четвёртая корзина. Такое решение у нас уже было в варианте номер 3.
Вариант 6: корзина с 44 яблоками (седьмая) + что-то ещё. Раз у нас 72 яблока, а в одной корзине их 44, то где-то ещё лежит 72 − 44 = 28 яблок — а это как раз третья корзина. Такое решение у нас уже было в варианте номер 2.
Вариант 7: корзина с 48 яблоками (седьмая) + что-то ещё. Раз у нас 72 яблока, а в одной корзине их 48, то где-то ещё лежит 72 − 48 = 24 яблок — а это как раз вторая корзина. Такое решение у нас уже было в варианте номер 1.
Получается, что у нас есть три равнозначных варианта корзин с грушовкой:
- Антоновка — в 5-й корзине, грушовка — в 1, 2 и 8-й (вариант 1).
- Антоновка — в 5-й корзине, грушовка — в 1, 3 и 7-й (вариант 2).
- Антоновка — в 5-й корзине, грушовка — в 1, 4 и 6-й (вариант 3).
Продали корзину с 48 яблоками
Здесь логика будет точно такая же: находим корзины, которые в сумме дадут нужное нам количество яблок, просто перебрав все возможные варианты, как в первом случае. Мы сделали это за вас, и вот что у нас получилось:
- Антоновка — в 4-й корзине, грушовка — в 1, 7 и 8-й.
- Антоновка — в 4-й корзине, грушовка — в 2, 6 и 8-й.
- Антоновка — в 4-й корзине, грушовка — в 3, 5 и 8-й.
Как видите, программисту для решения пришлось быстро перебрать все возможные комбинации, которые могут быть, и отбросить те, что не дают верного ответа. На то он и умный программист.
Чтобы не заниматься сложными вычислениями, напишем скрипт, который сделает так:
- По очереди смоделирует покупку одной корзины.
- Проверит, выполняется ли условие, что одних яблок в 2 и 4 раза больше, чем других.
- Если выполняется — добавит это как решение.
- В конце выведет все найденные решения.
Это не так изящно, как решить задачу с учётом всех нюансов, но зато быстро. Читайте комментарии и смотрите на ответ:
# все корзины с яблоками
apple = [20, 24, 28, 32, 36, 40, 44, 48]
# библиотека для перестановок
import itertools
# тут будет результат
res = []
# перебираем все корзины
for i in range(8):
# делаем копию массива с яблоками
new_apple = apple.copy()
# покупаем очередную корзину
new_apple.pop(i)
# получаем все варианты перестановок из оставшихся корзин
l = list(itertools.permutations(new_apple))
# перебираем все перестановки
for j in range(len(l)):
# если условие выполняется, проверяем такую комбинацию количества корзин: 1 → 2 → 4
if 2 * l[j][0] == l[j][1] + l[j][2] and 4 * l[j][0] == l[j][3] + l[j][4] + l[j][5] + l[j][6] or 2 * l[j][0] == l[j][1] + l[j][2] + l[j][3] and 4 * l[j][0] == l[j][4] + l[j][5] + l[j][6]:
# формируем очередной ответ
text = 'Антоновка — в корзине где ' + str(l[j][0]) + ' яблок, грушовка — где в корзинах ' + str(l[j][1]) + ', ' + str(l[j][2]) + ' и ' + str(apple[i]) + ' яблок '
# если такого ответа ещё нет — добавляем в список
if text not in res:
res.append(text)
# то же самое для другой комбинации корзин (1 → 3 → 3)
for j in range(len(l)):
if 2 * l[j][0] == l[j][1] + l[j][2] + l[j][3] and 4 * l[j][0] == l[j][4] + l[j][5] + l[j][6] or 2 * l[j][0] == l[j][1] + l[j][2] + l[j][3] and 4 * l[j][0] == l[j][4] + l[j][5] + l[j][6]:
text = 'Антоновка — в корзине где ' + str(l[j][0]) + ' яблок, грушовка — где в корзинах ' + str(l[j][1]) + ', ' + str(l[j][2]) + str(l[j][3]) + ', ' + ' и ' + str(apple[i]) + ' яблок '
if text not in res:
res.append(text)
#
for a in res:
print(a)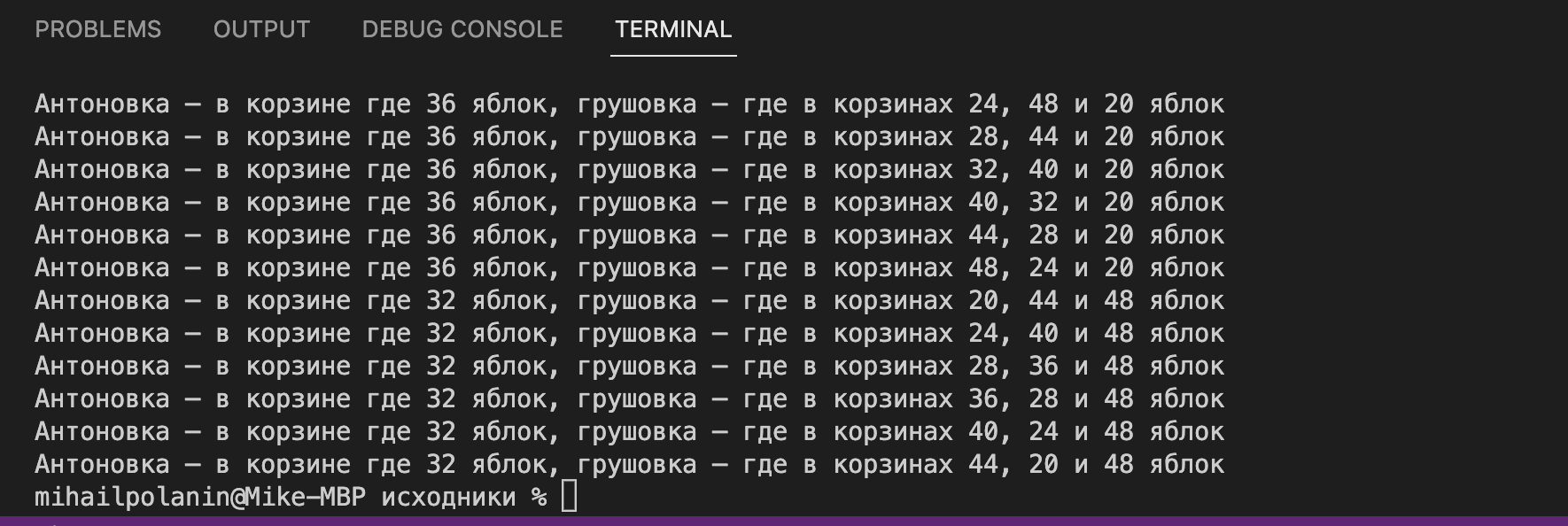
Видно, что у нас повторяются корзины в ответах, потому что они стоят в разном порядке, но по сути всё верно: мы нашли все варианты распределения разных сортов по корзинам. В этом и сила программирования — можно поручить машине отобрать для нас подходящие варианты, чтобы из них мы быстро собрали правильный ответ.