Ссылку на эту статью можете использовать, чтобы проверить базовые математические навыки любого человека. Кидаете ему ссылку и просите при вас (не читая решения) порешать какие угодно задачки. Все эти задачки уже у нас были в разное время в этом году. Поэтому если вы наш хардкорный читатель с самого марта, то можете спокойно медитировать следующие пять минут, это кайф.
Таракан на стене
В ваш подъезд двумя этажами ниже въехали новые жильцы, которые привезли с собой тараканов, но не привезли еды. Насекомые в поисках еды стали ползти вверх по вентиляционной шахте и скоро доберутся до вашей квартиры. Но карабкаться вверх им неудобно: за час они поднимаются на 1 м, но сразу после этого теряют равновесие и скатываются на ⅔ м вниз.
Вопрос: сколько часов у вас есть на покупку ловушек для тараканов, если расстояние от вас до соседей по вентиляционной шахте — 7 м?
За один полный час таракан проползает ⅓ м: поднимается на метр и опускается на ⅔:
1 — ⅔ = ⅓ м — проползает таракан за час.
С другой стороны, последний метр таракан проползёт тоже за 1 час: он доберётся до верха за 60 минут, но скатываться вниз ему уже не надо, потому что он достиг ровной поверхности. Значит, нужно узнать, сколько времени ему понадобится на оставшиеся 6 м:
7 м до вас — 1 м, который он проползёт за один заход = 6 м, которые таракан будет медленно ползти и скатываться.
Чтобы узнать оставшееся время, разделим расстояние на скорость:
6 м / ⅓ м в час = 18 часов.
Получается, что таракан проползёт 6 м за 18 часов, а оставшийся метр преодолеет за час, потому что скатываться уже не придётся. Получаем общее время:
18 + 1 = 19 часов.
Значит, у вас есть 19 часов на то, чтобы купить ловушки и гель от тараканов. Логика!
Долгий перелёт
Представьте, что вам нужно пару раз по работе слетать из Москвы во Владивосток и вернуться назад. Первый раз вы летите туда и обратно при полном штиле. Во второй раз при точно таком же перелёте в оба конца постоянно дует западный ветер одинаковой силы: туда попутный, а обратно — лобовой. Как изменится общее время полёта во втором случае: уменьшится, увеличится или останется таким же, как в первом случае?
Самая первая реакция на такую задачу — сказать, что время не изменится. Всё кажется логичным: когда летишь туда, ветер чуть ускоряет самолёт, а когда обратно — точно так же замедляет. Но это верно только наполовину.
В рамках задачи примем скорость самолёта за 800 километров в час. А ветер пусть дует со скоростью 100 километров в час. Мы знаем, что в реальных условиях всё намного сложнее и скорости нельзя складывать напрямую, но для упрощения допустим, что это возможно. Расстояние от Москвы до Владивостока по воздуху — 6 400 километров.
Первая командировка — без ветра
Если ветра нет, то у нас есть только скорость самолёта, которая не меняется в обоих случаях. Расстояние тоже одинаковое, значит время полёта будет неизменным в путешествии туда и обратно. Найдём его:
6 400 / 800 = 8 часов.
Это значит, что в безветренную погоду наш самолёт будет лететь из Москвы во Владивосток 8 часов, и столько же лететь обратно. В сумме — 16 часов.
Вторая командировка — дует постоянный ветер
Когда летишь во Владивосток и дует попутный ветер, самолёт и в самом деле летит быстрее: скорость последнего складывается со скоростью ветра.
800 + 100 = 900 (км/ч).
Тогда самолёт наше расстояние пройдёт за 7 часов 7 минут:
6 400 / 900 = 7,11 часа.
Когда летишь обратно и дует встречный ветер, то скорость самолёта падает:
800 - 100 = 700 (км/ч).
И путь обратно он с этой скоростью проделает уже за 9 часов 8 минут:
6 400 / 700 = 9,14 часа.
Получается, что общее время туда и обратно при таком ветре будет равно:
7 часов 7 минут + 9 часов 8 минут = 16 часов 15 минут.
Постоянный ветер увеличивает общее время полёта, и чем сильнее ветер — тем больше времени займёт полёт.
Если ветер будет дуть в 3 раза сильнее — 300 километров в час, то до Владивостока самолёт долетит за 5 часов 48 минут, а обратно ему потребуется уже 12 часов 48 минут, что в сумме даст 18 часов 36 минут.
Но почему?
Потому что математика:
6 400 / 800 + 6 400 / 800 = 16.
6 400 / 900 + 6 400 / 700 = 16,25.
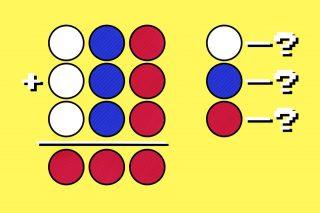 Задача на 60 секунд: что должно стоять вместо цветных шаров?
Задача на 60 секунд: что должно стоять вместо цветных шаров? Быстрая задача про время
Быстрая задача про время Логическая задача про странные часы
Логическая задача про странные часы Задача про время на сервере
Задача про время на сервере Вы не сможете решить эту задачу про повышение и пароль
Вы не сможете решить эту задачу про повышение и пароль Логическая задача про джуна, мидла и их дни рождения
Логическая задача про джуна, мидла и их дни рождения Нереальная задача про программистов и их логическое мышление
Нереальная задача про программистов и их логическое мышлениеПолторы белки
Полторы белки за полторы минуты съедают полтора ореха. Сколько орехов съедят 9 белок за 9 минут?
Первое, что хочется сразу ответить — 9 орехов. Но это было бы слишком просто.
Самое безумное в этой задаче — полторы белки. Давайте от них избавимся и будем дальше работать уже с целыми животными.
Дальше в решении будем исходить из того, что белки всё едят одновременно друг с другом, независимо от их количества. В обычной жизни так и происходит, и мы тоже будем придерживаться того же.
Узнаем, на что способна одна белка за полторы минуты:
1,5 белки за 1,5 минуты съедают 1,5 ореха → 1 белка за те же 1,5 минуты съест 1 орех.
Теперь выясним, сколько орехов она съест за 9 минут. Для этого нам нужно полторы минуты умножить на 6, а значит и количество съеденного тоже нужно умножить на 6:
1 белка за (1,5 * 6) минут съест (1 * 6) орехов
↓
1 белка за 9 минут съест 6 орехов.
Осталось запустить 9 белок одновременно и посчитать, сколько орехов они осилят за те же 9 минут:
(1 * 9) белок за 9 минут съедят (6 * 9) орехов
↓
9 белок за 9 минут съедят 54 ореха!
Почему? Потому что математика!
Рекрутер и бесконечный офис
В одной крупной компании появился безумный рекрутер, который нанимал на работу только джуниоров. У него был хитрый план — заполнить ими весь офис и получить за это премию от начальства. Чтобы это сделать, он каждый день нанимал столько же людей, сколько уже работает в офисе. Грубо говоря, удваивал число джуниоров.
Когда он только начинал, в старом офисе работал только один джуниор, но 30 дней спустя все рабочие места в офисе были полностью заняты напуганными, ничего не понимающими джуниорами.
В новом, точно таком же по размеру офисе с первого дня работает в 2 раза больше людей, чем на старте в старом — целых 2 джуниора вместо одного. Сколько времени уйдёт у безумного рекрутера на то, чтобы заполнить новый офис и получить свою квартальную премию?
Казалось бы, что если на старте в 2 раза больше людей, то и новый офис заполнится быстрее в 2 раза — за 15 дней вместо 30, но это не так.
Смысл в том, что, по условию задачи, рекрутер удваивает число людей каждый день. Это значит, что в новом офисе это удвоение произошло фактически на день раньше, чем в старом, а значит, и джуниоры его полностью займут только на день раньше — за 29 дней вместо 30.
Если вы любите точные математические решения вместо рассуждений — вот решение. Сначала посчитаем, сколько людей всего вмещает каждый офис. Для этого запишем каждые удвоения начиная с одного джуниора:
день 1: 1 джуниор
день 2: 2 джуниора
день 3: 4 джуниора
день 4: 8 джуниоров . . .
Если вывести общую формулу, получим:
день 1: 2 в нулевой степени джуниоров
день 2: 2¹ джуниоров
день 3: 2² джуниоров
день 4: 2³ джуниоров
. . .
день 30: 2 в 29-й степени джуниоров
Получается, что наш офис вмещает 2 в 29-й степени джуниоров. Если удвоение происходит каждый день и на старте у нас 2 джуниора, то для нового офиса получим такое уравнение, где х — количество дней:
2 в 29-й степени = 2 в степени х
Очевидно, что х = 29, а, значит, на заполнение всего нового офиса понадобится 29 дней, как мы и говорили в начале.
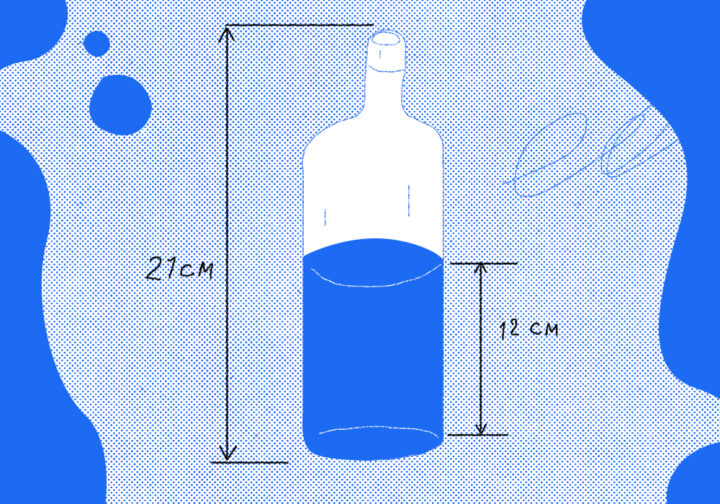
Задача про бармена и гурмана
У бармена эксклюзивного лофт-хипста-бара на улице Рубинштейна есть только два одинаковых стакана по 150 мл. Один стакан — полный, и в нём простая вода, а в другом 40-градусная водка, и он наполовину пуст. Утро-с.
В бар зашёл посетитель и попросил сделать ему 15-градусный раствор спирта. Находчивый бармен не растерялся и смог приготовить его, используя только эти два стакана. Как он это сделал и какой объём получился в итоге?
Вряд ли эта задача когда-нибудь попадётся на собеседовании в ИТ-компанию, но она может пригодиться в реальной жизни — например, завтра.
Это вариант классической задачи на переливания, только надо считать ещё крепость раствора и его объём.
Берём полупустой стакан с водкой и доливаем в него воды до полного. Получаем целый стакан 20-градусного спирта ((40 + 0) / 2 = 20). Во втором стакане осталась половина чистой воды, она нам сейчас пригодится.
В стакан с оставшейся водой наливаем наш раствор спирта — снова до краёв. В нём теперь 10 градусов ((20 + 0) / 2 = 10). В другом осталось полстакана 20-градусного спирта.
Финальным этапом бармен берёт и разбавляет эти полстакана 10-градусным раствором из полного стакана так, чтобы жидкость снова дошла до края. В итоге получается 15-градусный раствор ((20 + 10) / 2 = 15) объёмом в 150 мл!
Популярная школьная задача
Вот вам очень простой математический пример:
8 / 2(2 + 2)
Вы удивитесь, но большинство людей не смогут правильно это посчитать. Посчитайте сами и потом смотрите правильный ответ:
В интернете много споров про такие примеры, поэтому мы решили разобраться, какие ошибки совершают чаще всего и почему многие считают неправильно. Для решения нам понадобятся три математических правила:
- То, что в скобках, выполняется в первую очередь. Если скобок несколько, они выполняются слева направо.
- При отсутствии скобок математические действия выполняются слева направо, сначала умножение и деление, потом — сложение и вычитание.
- Между множителем и скобкой (или двумя скобками) может опускаться знак умножения.
Разберём подробнее, что это значит в нашем случае.
1. То, что в скобках, выполняется в первую очередь. То есть в нашем примере, вне зависимости от чего угодно, сначала схлопнутся скобки:
8 / 2(2 + 2) → 8 / 2(4)
2. Между числом и скобкой можно опустить знак умножения. У нас перед скобкой двойка, то есть можно сделать такую замену:
8 / 2(4) → 8 / 2 × 4
3. Математические действия при отсутствии скобок выполняются слева направо: как при чтении, сначала умножение и деление, потом — сложение и вычитание. Умножение и деление имеют одинаковый приоритет. Нет такого, что сначала всегда делается умножение, затем деление, или наоборот. Со сложением и вычитанием то же самое.
Некоторые считают, что раз множители были написаны близко друг к другу (когда там стояли скобки), то оно выполняется в первую очередь, ссылаясь при этом на разные методические пособия. На самом деле это не так, и нет такого скрытого умножения, которое имеет приоритет над другим умножением или делением. Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.
Получается, что нам сначала надо сложить 2 + 2 в скобках, потом 8 разделить на 2, и полученный результат умножить на то, что в скобках:
8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16
Кстати, если на айфоне записать это выражение точно так же, как в условии, телефон тоже даст правильный ответ.
А инженерный калькулятор на Windows 10 так записывать не умеет и пропускает первую двойку-множитель. Попробуйте сами :)
Тут в тред врываются математики и с воплями «Шустеф!» поясняют криком:
«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c)».
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
Раз в спорном примере знак умножения опущен, то спорный пример алгебраический, а значит, сначала умножаем 2 на 4, а потом 8 делим на 8!

А вот как на это отвечают те, кто действительно в теме и не ленится полностью посмотреть первоисточник:
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87]. П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20×2=80:40=2 вместо обычного: 80:20×2=4×2=8. Однако это предложение не нашло поддержки».
Если апеллировать к Фриде Максовне Шустеф, то выходит, что:
- В. Л. Гончаров говорит так: «Ребята, используйте черту и ставьте скобки, чтобы ни у кого не было вопросов про приоритет».
- Если у нас всё же битва арифметики и алгебры, то, по П. С. Александрову и А. Н. Колмогорову, пример нужно решать слева направо, как обычно. Они, конечно, предложили решать такое по-другому, но научное сообщество их не поддержало.
Самое интересное, что дальше в примерах Фрида Максовна пользуется как раз правильным порядком действий, объясняя решение. Даже там, где есть умножение на скобку с опущенным знаком, она выполняет действия слева направо.

Что не так с отчётом?
Один требовательный HR-директор дал задание менеджеру: провести опрос среди веб-программистов и выяснить, на каком языке они пишут чаще всего — на JavaScript или на PHP. Через неделю менеджер принёс такой отчёт:
- количество опрошенных — 300;
- умеет писать на JavaScript — 234;
- умеет писать на PHP — 213;
- умеют писать на обоих языках — 144;
- вообще не пишут код — 0.
HR-директор посмотрел на отчёт и сказал менеджеру «У тебя ошибка в отчёте. Данные фальсифицированы. Ты уволен в связи с утратой доверия». За какую ошибку уволили менеджера?
Чтобы найти ошибку, давайте проверим цифры из отчёта и сравним их с исходными. Для начала выясним, кто умеет писать ТОЛЬКО на JavaScript. Чтобы это сделать, возьмём тех, кто умеет на нём писать, и вычтем оттуда тех, кто пишет на обоих языках:
234 − 144 = 90 (чистых JavaScript-программистов)
Точно так же посчитаем тех, кто пишет ТОЛЬКО на PHP: возьмём общее количество PHP-программистов и вычтем из них тех, кто умеет писать на обоих языках.
213 − 144 = 69 (чистых PHP-программистов)
А теперь сложим три группы: тех, кто пишет только на JavaScript (90 человек), кто пишет только на PHP (69 человек) и тех, кто пишет на двух языках сразу (144 человека).
90 + 69 + 144 = 303
Получилось 303 человека, а в опросе заявлено 300.
Понятно, что расхождение в 3 человека не влияет на общую статистику, но для требовательного HR-директора этого было достаточно.
Программисты и часы
— Доброе утро. Который сейчас час?
— Сложи 1/4 времени, прошедшего с полуночи до сейчас, с 1/2 от сейчас до полуночи.
— Спасибо, я понял.
— Не сомневался.
Вопрос: который час?
На самом деле это очень простая задача, если помнить, что в сутках 24 часа.
Пусть от полуночи до сейчас прошло Х времени. Тогда от сейчас до полуночи осталось 24 – Х времени.
С другой стороны, если мы сложим четверть времени от полуночи до сейчас и половину времени от сейчас до полуночи, то как раз получим Х — время, которое сейчас:
(¼ × Х) + (½ × (24 − Х)) = Х
Раскрываем скобки:
Х/4 + 12 − Х/2 = Х
Перенесём все Х в одну сторону, а 12 — в другую:
Х − Х/4 + Х/2 = 12
Х + Х/4 = 12
5Х/4 = 12
5Х = 48
Х = 9,6
Получается, что с полуночи прошло 9,6 часа, или 9 часов 36 минут.
Ответ: на часах 9:36.
Необычный автосалон
Один автосалон купил подержанную машину за 450 тысяч и через неделю продал её за 525 тысяч. Директор салона решил, что такая модель пользуется спросом, так что он дал менеджерам задание — найти ещё одну подобную машину. Они нашли такую же за 550 тысяч, купили её, но директор повёл себя странно. Он снова поставил на неё ценник в 525 тысяч, и машина ушла за два дня. Помогите бухгалтерии понять, заработал в итоге салон или потерял часть денег?
У этой задачи три решения: интуитивное, пошаговое и бухгалтерское. Сравните подходы.
Многие решают эту задачу так:
- Было 450 тысяч.
- Купили машину и продали за 525 тысяч.
- После продажи заработали 75.
- Взяли в долг 25.
- Купили вторую машину и продали снова за 525.
- Изначально было 450, стало 525, значит, прибыль снова составила 75 тысяч, а общая — 150 тысяч.
- Отдаём 25 долга, получаем прибыль 125 тысяч.
Но это неправильно. Правильно — ниже.
Давайте разберём эту сделку по шагам, чтобы понять, сколько денег было у салона на каждом этапе.
В самом начале у них было 450 тысяч — запомним это. Эти деньги пошли на покупку первой машины, поэтому на втором шаге у салона стало 0 рублей, но появился автомобиль.
На третьем шаге его продали за 525 тысяч, которые и ушли в кассу. Пока прибыль салона равна: 525 − 450 = 75 тысяч.
Вторая машина стоила на 25 тысяч дороже, чем у них было — 550, поэтому салон взял в долг 25 тысяч и купил её (шаг номер четыре). Здесь прибыль салона исчезла и появился убыток в 25 тысяч.
Пятым шагом они продали вторую машину за 525 тысяч, положили деньги в кассу и стали разбираться с долгами. После того как они вернули сумму, которую были должны, у салона осталось 500 тысяч, а начинали они с суммы в 450 тысяч. Получается, что они заработали 500 − 450 = 50 тысяч.
Бухгалтеры работают так: считают все доходы и расходы, а потом находят сальдо — разницу между ними. Сделаем то же самое.
Доходы: 525 с первой продажи и столько же со второй. Получается 525 + 525 = 1050 тысяч.
Расходы: 450 за первую машину и 550 за вторую. Получается 450 + 550 = 1000 тысяч.
Сальдо: доходы минус расходы. Это 1050 − 1000 = 50 тысяч.