У нас иногда выходят задачки. Сегодня — большая жирная подборка задач о математике и числах. Для решения достаточно школьной программы И ВАШЕГО НЕВЕРОЯТНОГО УМА.
Как выбрать банки
Сельское хозяйство на подъёме, и власти решили поддержать фермера из Вологды, который торгует молоком. Они сказали ему: «Мы знаем, что тебе нужно продавать до 40 л молока за раз, поэтому вот тебе деньги, купи любые четыре банки, чтобы ты мог ими точно отмерять 40 л или меньше, смотря сколько нужно покупателю».
Фермер обрадовался, но тут пришёл Роспотребнадзор и сказал: «Больше одного раза молоко в банку наливать и переливать нельзя, это негигиенично. Учитывай это при выборе тары». То есть при каждой продаже одному покупателю каждую банку допустимо использовать только один раз. Потом ёмкости можно мыть и применять заново с новым покупателем.
Вопрос. Какого объёма банки нужно купить фермеру, чтобы иметь возможность отмерить ими от 1 до 40 л, используя любую из них только по одному разу?
Первая банка
Самый маленький объём, который нам нужен — 1 л. Сразу купим эту банку и посмотрим, приведёт ли это нас к верному решению.
Вторая банка
Теперь мы с первой ёмкостью можем отмерять 1 л, но не более. Надо добавить вторую банку и использовать её по максимуму. Это значит, что разница в объёме между первой и второй ёмкостями должна быть как можно больше. Проверим банки на 2, 3 и 4 л.
- Двухлитровая. С её помощью мы можем отмерить 1 л (первой банкой), 2 л (второй банкой) и 3 л (сумма первой и второй, обозначим как 1 + 2). Негусто.
- Трёхлитровая. Теперь мы отмеряем 1 л (первая банка), 2 л (наливаем 3 л в большую банку, сливаем литр в маленькую), 3 л (вторая банка) и 4 л (3 + 1). Уже лучше.
- Четырёхлитровая. С ней мы не сможем отмерить 2 л. Значит, эта банка нам не подходит и вторая ёмкость будет на 3 л.
Вывод: второй мы покупаем трёхлитровую банку.
Третья банка
Мы уже умеем отмерять 4 л двумя банками, а 5 л будем наливать уже тремя.
Раз нам нужна тара как можно больше, нужно сделать так, чтобы 5 л у нас получилось, когда мы из третьей банки заберём 4 л. Это максимальный объём, который мы можем из неё взять первыми двумя ёмкостями. Найдём объём третьей банки:
4 + 5 = 9 (литров)
Проверим, сколько литров можем отмерить этими тремя банками:
5 л = 9 − 3 − 1 (отливаем всё из третьей в первые две)
6 л = 9 − 3
7 л = 9 − 3 + 1
8 л = 9 − 1
9 л = 9 (третья банка)
10 = 9 + 1
11 = 9 + 3 − 1
12 = 9 + 3
13 = 9 + 3 + 1 (наполняем все три банки)
Отлично, значит, третья банка на 9 л нам подходит.
Четвёртая банка
Мы остановились на 13 л, и нужно перейти к 14 л. Снова применим ту же тактику и поищем наибольшую банку, из которой можно забрать 13 л, чтобы осталось 14:
13 + 14 = 27 (литров)
Проверим эту банку:
14 = 27 − 9 − 3 − 1 (отливаем всё в первые три)
15 = 27 − 9 − 3
16 = 27 − 9 − 3 + 1
17 = 27 − 9 − 1
18 = 27 − 9 (отливаем в третью)
19 = 27 − 9 + 1
20 = 27 − 9 + 3 − 1
21 = 27 − 9 + 3
22 = 27 − 9 + 3 + 1
23 = 27 − 3 − 1
24 = 27 − 3 (отливаем во вторую)
25 = 27 − 3 + 1
26 = 27 − 1 (отливаем в первую)
27 = 27 (четвёртая банка)
28 = 27 + 1 (четвёртая и первая)
29 = 27 + 3 − 1
30 = 27 + 3 (четвёртая и вторая)
31 = 27 + 3 + 1
32 = 27 + 9 − 3 − 1
33 = 27 + 9 − 3
34 = 27 + 9 − 3 + 1
35 = 27 + 9 − 1
36 = 27 + 9 (четвёртая и третья)
37 = 27 + 9 + 1
38 = 27 + 9 + 3 − 1
39 = 27 + 9 + 3
40 = 27 + 9 + 3 + 1 (заполняем все четыре банки)
Всё сошлось, и нам подходит четвёртая ёмкость на 27 л.
Ответ
Нам нужно купить банки на 1, 3, 9 и 27 л.
Захватят ли наноботы мир?
Нашу планету ровным слоем покрывает большая колония бактерий, которые находятся буквально везде. Внезапно в Сколкове изобретают высокотехнологичных наноботов, которые имеют способность самовоспроизводиться при съедании этих бактерий. Каждую секунду сколковский нанобот пожирает одну бактерию и сразу делится на два таких же нанобота. Бактерии просто питаются подножным кормом и тоже каждую секунду делятся пополам, но просто так, сами по себе.
Захватят ли сколковские наноботы всю планету, если вырвутся из не очень хорошо охраняемых сколковских лабораторий и начнут размножаться в дикой природе?
Эта задача красиво решается через обычные школьные уравнения, но для этого нужно будет добавить два неизвестных.
Каждый нанобот съедает по одной бактерии и тут же делится пополам, то есть на каждом шаге количество наноботов удваивается. А раз так, то удваивается и количество съедаемых бактерий. Запишем, сколько бактерий съедает нанобот на каждой секунде:
секунда 0: 1 — потому что в самом начале у нас один нанобот
секунда 1: 2 × 1 — после первой секунды наноботов стало два, значит, они съели две бактерии, каждый по одной
секунда 2: 2 × 2 × 1 — наноботы снова удвоились и съели по бактерии
Мы видим постоянное произведение двоек, а значит, их можно представить в виде степени:
секунда 0: 1 = 2 в нулевой степени
секунда 1: 2 = 2¹
секунда 2: 4 = 2²
* * *
T секунда: 2 в степени Т
Мы выяснили, как быстро размножаются наноботы и сколько на каждой секунде они съедят бактерий. Теперь допустим, что когда на планете появился один нанобот, этих бактерий уже было N штук. Тогда снова обозначим время в секундах как Т и попробуем выяснить, сколько бы получалось бактерий на каждой секунде с учётом наноботов:
секунда 0: N — начальные условия
секунда 1: 2 × (N − 1) — перед удвоением наноботы съели одну бактерию
секунда 2: 2 × [ 2 × (N − 1) − 2] — удваиваем то, что было до этого, и перед этим вычитаем две съеденных бактерии
секунда 3: 2 × { 2 × [ 2 × (N − 1) − 2] − 4} — снова удваиваем предыдущее, не забывая вычитать съеденных бактерий.
Раскроем скобки и продолжим логический ряд:
секунда 0: N
секунда 1: 2 × N − 2
секунда 2: 2² × N − 8
секунда 3: 2³ × N − 24
* * *
секунда Т: (2 в степени Т) × N − (2 в степени T) × Т
Когда наноботы съедят всех бактерий и захватят мир, наше последнее уравнение станет равно нулю. Запишем это:
(2 в степени Т) × N − (2 в степени T) × Т = 0
Перенесём одну часть уравнения вправо:
(2 в степени Т) × N = (2 в степени T) × Т
Видим, что в каждой части есть общий множитель: (2 в степени Т). Сократим его:
N = Т
Получается, что наноботам, чтобы съесть всех бактерий, понадобится столько секунд, сколько бактерий было на планете в момент старта. А раз время у нас не ограничено, то в конце концов наноботы дожуют всех бактерий и ЗАХВАТЯТ ВЕСЬ МИР!
Проверим это для колонии из четырёх бактерий:
секунда 0: 4 бактерии и 1 нанобот
секунда 1: 6 бактерий и 2 нанобота
секунда 2: 8 бактерий и 4 нанобота
секунда 3: 8 бактерий и 8 наноботов
секунда 4: 0 бактерий и 16 наноботов
Решение работает, наноботы победили!
Делим неделимое
У старика было три сына. Перед смертью он оставил им завещание:
половину всего имущества — старшему сыну,
треть — среднему,
одну девятую — младшему.
Всё имущество старика — 17 лошадей. Как поделить лошадей между братьями, чтобы выполнить завещание отца?
Эту задачу можно решить несколькими способами, но есть одно классическое решение и несколько современных. Если вы нашли решение, которое здесь не описано, поздравляем — вы гораздо умнее, чем автор!
Классическое решение
Проблема здесь в том, что отец или не знал правила деления, или был очень хитрым, потому что, если подходить к решению прямо, то 17 лошадей не делятся поровну на 2, 3 и 9. Ближайшее число, которое это умеет делать — 18, но нам тогда не хватает одной лошади. Но допустим, что правила он всё-таки знал, и решил просто проверить братьев, как они выйдут из этой ситуации.
Мы тоже пойдём на хитрость — для ровной делёжки между братьями мы одолжим одну лошадь в соседнем табуне, а потом вернём её обратно. Это поможет нам выполнить условия завещания, не изменяя общего числа лошадей у братьев.
Теперь у нас 18 лошадей, и мы можем делить наследство:
старший — 18 : 2 = 9 лошадей
средний — 18 : 3 = 6 лошадей
младший — 18 : 9 = 2 лошади.
Получается, что всего у братьев 9 + 6 + 2 = 17 лошадей, как раз столько и завещал им отец! Восемнадцатую лошадь, которую мы одалживали, и которая не принимала участия в расчётах, мы просто возвращаем хозяевам и благодарим их за помощь.
Хитрость и смекалка!
Правда, тут надо сказать, что в момент добавления лошади к отцовскому имуществу его общий объем изменился, и мы, получается, нарушили условия задачи. Зато кони целы.
Логическое решение
Для начала давайте посчитаем доли, которые должны достаться каждому брату:
старший — 1/2 = 9/18
средний — 1/3 = 6/18
младший — 1/9 = 2/18
Если сложить все доли, получим 17/18. И как только мы в числителе видим 17 — ровно столько, сколько у нас лошадей — понимаем, что этим можно воспользоваться.
17/18 — это 17 лошадей, а это значит, что:
9/18 — это 9 лошадей для старшего
6/18 — это 6 лошадей для среднего
2/18 — это 2 лошади для младшего
В итоге мы поделили все 17 лошадей точно по долям отца из завещания.
Логика!
Математическое решение
Подойдём к процессу формально и разделим 17 лошадей так:
старшему — 17 / 2 = 8,5 лошадей
среднему — 17 / 3 = 5,6 лошадей
младшему — 1,88 лошадей
Если мы округлим все числа до целого вверх, то получим верные 9, 6 и 2, как и в предыдущем решении.
Если же отбросим дробные части, то у братьев будет 8, 5 и 1 лошадь, что в сумме даст 14. Остальные три лошади мы поровну поделим между братьями, и у них снова будет 9, 6 и 2 лошади соответственно.
Математика!
Рыночное решение
Есть ещё один способ поделить наследство — продать всех лошадей, а выручку поделить между братьями. Единственное, что нужно учесть — чтобы сумма продажи делилась одновременно на 2, 3 и 9 частей, иначе будет так же, как с лошадьми.
Экономика!
Бинарные мыши
В задаче про мышей и испорченную партию лекарства у нас было 10 мышей и 1000 пробирок. В одной из пробирок яд. Нужно было проверить, в какой пробирке яд, за минимальное количество дней.
Классическое решение — начать делить пробирки по количеству мышей. Например, сначала разделить пробирки на 10 групп по 100; взять из каждой по капле; скормить мышам. Одна мышь умрёт — тогда эту группу пробирок делим снова на оставшихся мышей. Так за три-четыре деления мы найдём пробирку с ядом.
Но что если отравленную пробирку надо найти за одно измерение? Возможно ли это?
Чтобы найти пробирку с ядом за один день, нам надо призвать на помощь двоичную систему счисления. Но для начала разберёмся с привычной — десятичной.
Десятичная система счисления
Она самая знакомая из всех, и мы ей пользуемся каждый день. В её основе — 10 цифр, от 0 до 9, поэтому она и называется десятичной.
Мы пользуемся десятичной системой, особо не рефлексируя. Например, мы видим число 436 — мы автоматически его раскладываем: четыре сотни + три десятка + шесть.
Только что мы разложили число на разряды: 4 — это разряд сотен, 3 — разряд десятков, 6 — разряд единиц. Получается, что:
436 = (4 × 100) + (3 × 10) + (6 × 1)
436 = (4 × 10²) + (3 × 10¹) + (6 × 10 в нулевой степени)
Получается, что наша десятичная запись числа — это просто краткая форма записи длинного выражения, где какие-то числа умножаются на десятки в разных степенях.
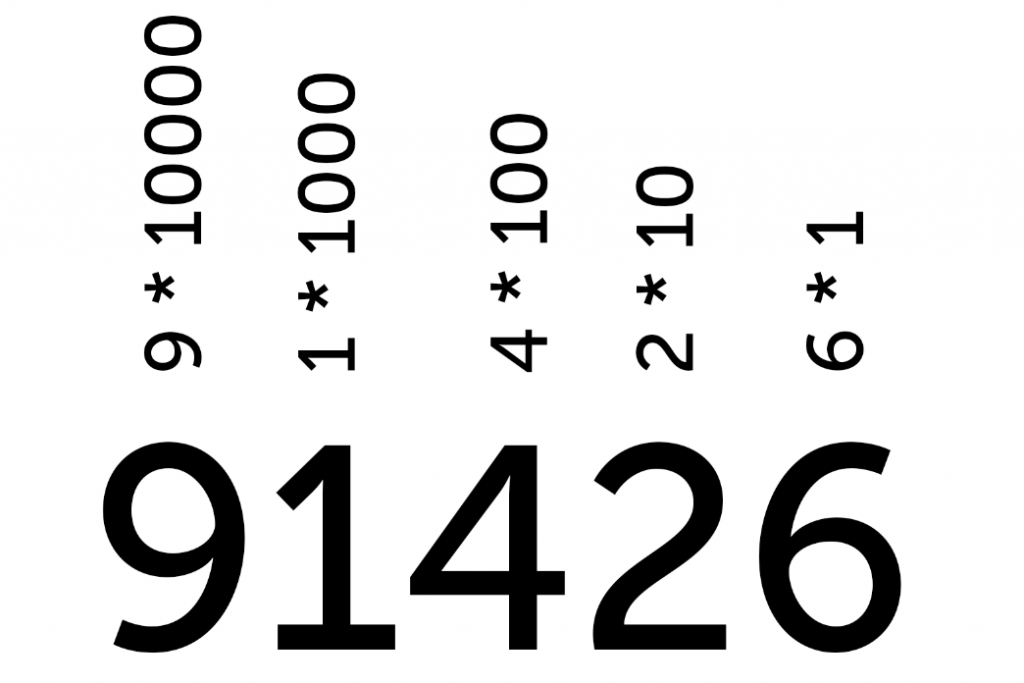
Двоичная система
Двоичная система — это то же самое, только вместо десятки — двойка. Вместо степеней десятки мы используем степени двойки. Вместо десяти цифр от 0 до 9 мы используем две: 0 и 1.
Чтобы перевести числа из двоичной системы счисления в десятичную, нужно то же самое, что и раньше: возводить двойку в степень разряда и умножать на 0 или 1. Рассмотрим на примере:
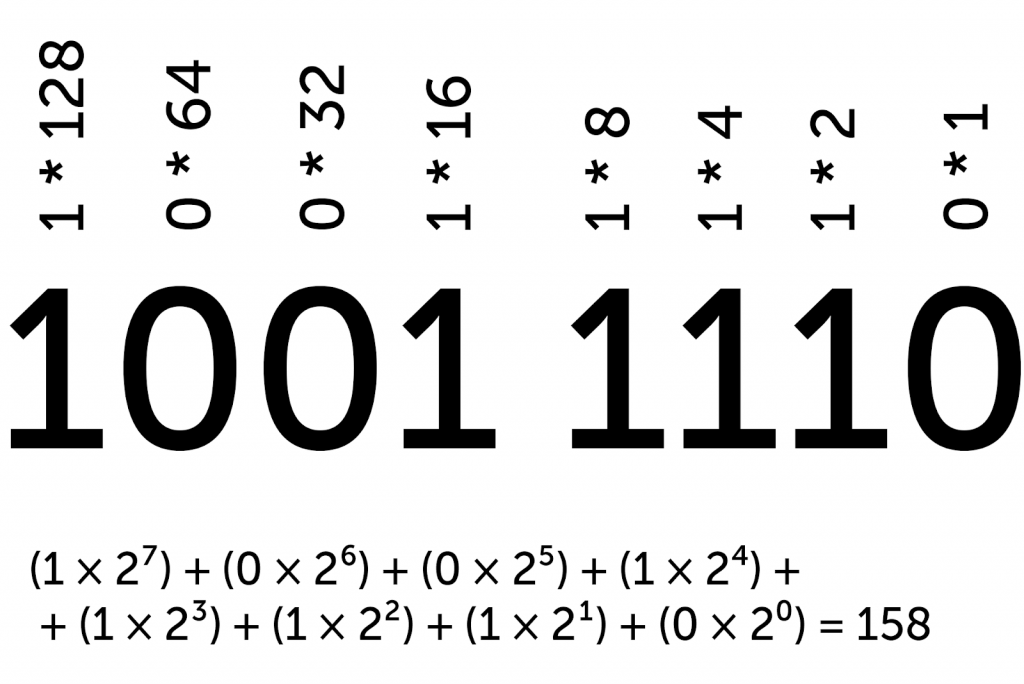
Любое десятичное число можно представить в виде двоичного, и наоборот. Теперь попробуем использовать это знание в решении задачи.
Битовая глубина
У нас 1000 пробирок. Запишем это число в двоичной системе счисления:
1000 в десятичной = 1111101000 в двоичной
Это максимальное число, которое нам понадобится при нумерации, и оно состоит из 10 нолей и единиц. Получается, что битовая глубина решения этой задачи — 10. А у нас как раз 10 мышей. Это и будем использовать при расчётах.
Немного магии
Зная, что у нас 10 бит на число, пронумеруем каждую пробирку таким образом:
1 — 0000000001
2 — 0000000010
3 — 0000000011
4 — 0000000100
...
999 — 1111100111
1000 — 1111101000
Затем расставляем мышей в клетки по порядку, чтобы они никуда не бегали и всегда оставались на своих местах. Пусть клетки стоят слева направо.
А теперь начинается магия. Берём каждую пробирку и смотрим, на каких местах стоят единицы. Мышам в этих клетках даём каплю вещества:
первая пробирка: 0000000001 — даём каплю мыши в самой правой клетке
вторая пробирка: 0000000010 — даём каплю мыши во второй клетке справа
третья пробирка: 0000000011 — даём по капле двум мышам из первой и второй клеток справа
четвёртая пробирка: 0000000100 — даём каплю мыши третьей клетке справа
...
999 пробирка: 1111100111 — даём по капле мышам из первых пяти клеток слева, пропускаем две клетки, дальше капаем трём оставшимся
Таким образом, каждая пробирка получила свою уникальную комбинацию из мышей. И на следующий день, когда часть мышей умрёт, мы сразу узнаем номер пробирки с ядом: оставшихся в живых мышей запишем как 0, а погибших — как 1.
Например, наутро мы заметили, что шесть мышей слева и одна справа живы, остальные три мертвы. Запишем это в двоичной системе:
0000001110
Переведём вручную или на калькуляторе это в десятичную систему и получим число 14. Это и есть номер нашей пробирки с ядом.
В чём секрет
Секрет в том, что комбинация нолей и единиц уникальна для каждой пробирки. И раз мы даём по капле тем мышам, которые соответствуют единице, то если в них будет яд, помечать их тоже надо единицами, чтобы восстановить картину. Комбинация погибших мышей из-за своей уникальности и укажет нам на номер пробирки с ядом.
Хрустящая задача про наггетсы
Два школьника, Женя и Костя, обедали в кафе. У Жени было с собой 4 наггетса, а у Кости — 7. К ним подошёл одноклассник Антон и предложил пообедать вместе, а в конце он бы расплатился за угощение. Ребята согласились и разделили 11 наггетсов поровну на троих.
После обеда Антон сказал «Ребята, у меня с собой как раз 110 рублей — сможете разделить их между собой?». «Конечно» — ответили друзья, после чего одноклассник отдал им деньги и ушёл.
Женя сказал, что раз делили всё поровну, то и деньги надо поделить поровну, то есть пополам — по 55 рублей каждому.
Костя в ответ сказал, что так нечестно, и раз у Жени было 4 наггетса, то он и получит 40 рублей, а Костя за свои 7 должен получить 70 рублей.
Кто из ребят прав и почему?
Оба школьника неправы.
Раз 11 наггетсов разделили поровну на троих, то каждому досталось по 11/3 от всех наггетсов.
У Жени было 4 наггетса: 4 = 12/3. Раз каждый съел по 11/3, то Антону от Жени досталось всего ⅓ наггетса.
У Кости наггетсов было 7: 7 = 21/3. Он съел 11/3, а значит 10/3 из своих запасов он отдал Антону:
21/3 − 11/3 = 10/3
Раз Антон тоже, как и все, съел 11/3 всего обеда и заплатил за это 110 рублей, то получается, что за каждую ⅓ он заплатил по 10 рублей. Поэтому нужно умножить вклад каждого по ⅓ на 10, чтобы понять, сколько денег ему причитается:
Жене — ( ⅓ / ⅓ ) × 10 = 1 × 10 = 10 рублей
Косте — (10 / 3 / ⅓ ) × 10 = 10 × 10 = 100 рублей