Вот логическая задачка на вероятности. Есть четыре шестигранных кубика, на каждом нанесены числа в такой комбинации:
на одном стоят числа 3, 3, 3, 3, 3, 3 (получается, на каждой стороне по тройке);
на втором — 0, 0, 4, 4, 4, 4 (две стороны с нулями, на остальных по четвёрке);
на третьем — 1, 1, 1, 5, 5, 5 (три стороны с единицами, три с пятёрками);
на четвёртом — 2, 2, 2, 2, 6, 6 (четыре с двойками, две с шестёрками).
Есть два игрока. Каждый выбирает кубик на всю игру. В каждом раунде участники кидают кубик и смотрят, у кого больше.
Всего в игре тысяча раундов. У кого больше побед за всю игру — тот и выиграл. Вы можете выбрать кубик первым. Какой кубик нужно выбрать, чтобы с наибольшей вероятностью выиграть?
Если вы не знаете, как подступиться к этой задаче, — почитайте нашу подборку лучших задач на вероятности и случайности. После этого разобраться с этой станет намного проще.
Раз игроки бросают кубик не один, а тысячу раз подряд, то победит тот, у кого будет выше вероятность получить за один бросок больше очков, чем у соперника. Вероятность — это насколько возможно, что произойдёт то, что нам нужно. Например, в обычном кубике 6 разных чисел, поэтому вероятность выпадения любого числа — ⅙.
Чтобы решить эту задачу, посчитаем вероятности выигрыша или проигрыша при выборе каждого из четырёх кубиков.
Тройки. Допустим, мы выбрали кубик с тройками, а соперник — кубик с четвёрками. Если у него выпадет 0, то он проиграет, потому что у нас всегда выпадает 3. Ноль у него выпадет 2 раза из 6, поэтому у него вероятность проиграть равна 2/6, или ⅓. При этом если у него выпадет 4, то он выиграет, а случится это 4 раза из 6 (потому что из 6 граней на 4 из них нарисована четвёрка).
Получается, что в этом случае соперник выиграет в 4/6, или ⅔ случаев. Это значит, что на дистанции в 1000 бросков мы в среднем выиграем 333 раза и проиграем 667 раз. Этот вариант не очень.
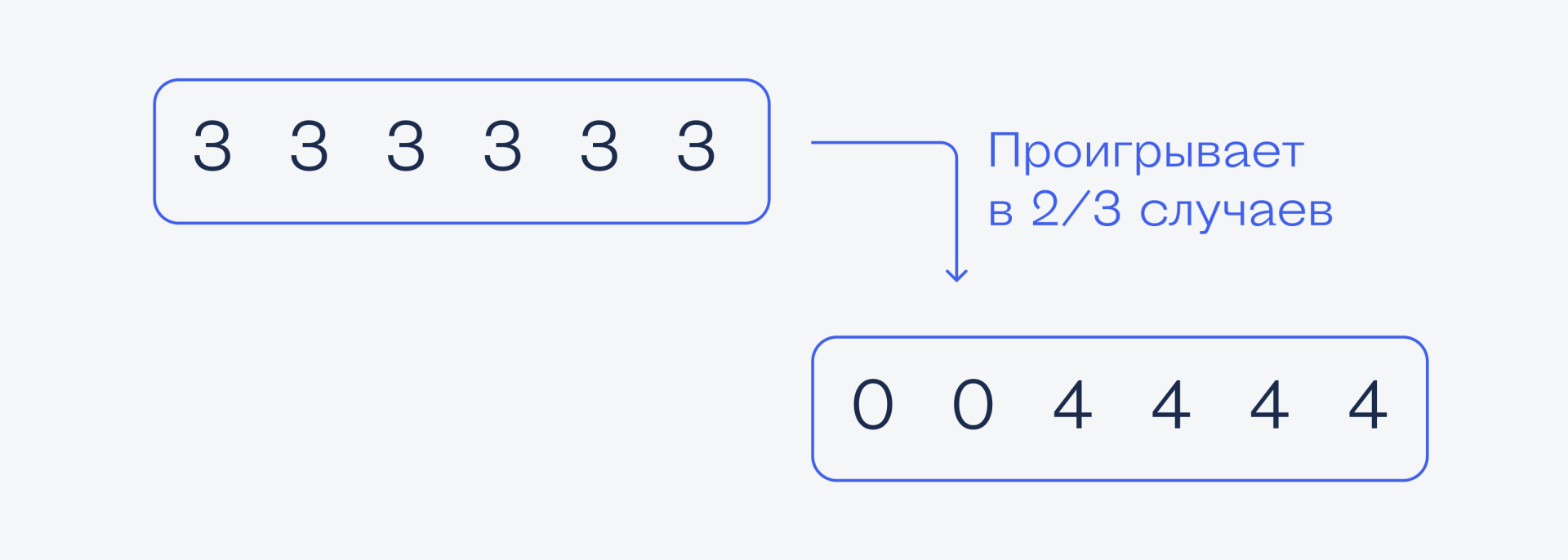
Четвёрки. Допустим, мы взяли кубик с четвёрками, а соперник — с пятёрками. В этом случае соперник точно выиграет, если у него выпадет 5 — потому что у нас только 0 и 4 (это значит, что вероятность выкинуть 0 или 4 у нас равна единице, то есть будет всегда). Пятёрка может выпасть в 3 случаях из 6, поэтому вероятность такого события равна 3/6, или ½. В остальной половине случаев, когда у него выпадает единица, мы всё равно можем проиграть, если у нас выпадет ноль. Ноль у нас выпадает 2 раза из 6, то есть с вероятностью ⅓.
Чтобы посчитать общую вероятность победы соперника, надо сложить все вероятности отдельных побед:
½ (у него выпало 5) × 1 (вероятность того, что у нас будет 0 или 4);
+
½ (у него выпало 1) × ⅓ (у нас выпал ноль);
=
½ + ⅙ = ⅔.
Получается, что если мы выберем кубик с четвёрками, а соперник — с пятёрками, то мы проиграем в ⅔ случаев. Так может, надо выбрать кубик с пятёрками?
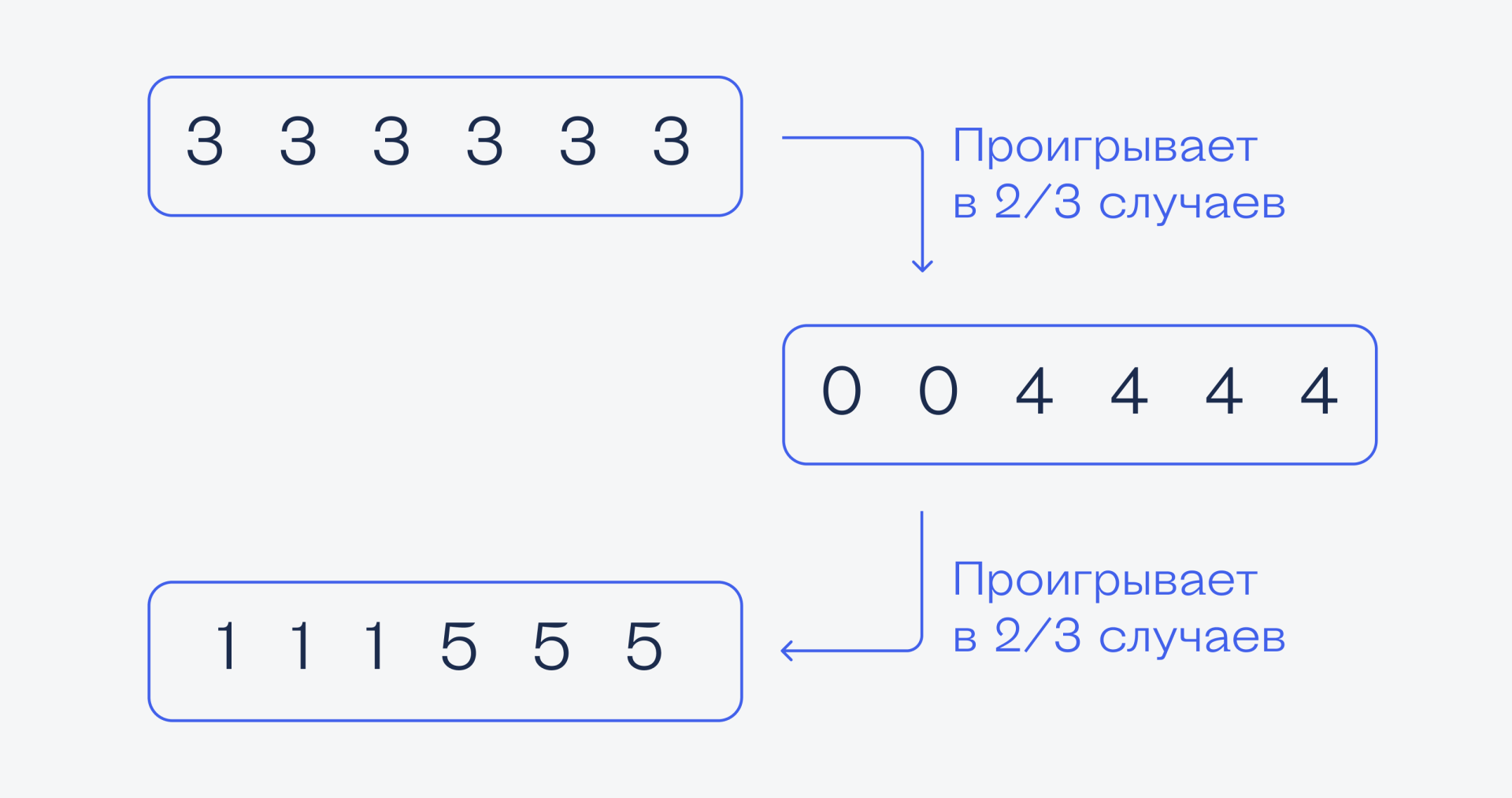
Пятерки. Допустим, мы выбрали кубик с пятёрками, а соперник — с шестёрками. В этом случае соперник точно выиграет, если у него выпадет 6 — потому что у нас только 1 и 5 (и вероятность проигрыша при этом равна единице). Шестёрка может выпасть в 2 случаях из 6, поэтому вероятность такого события равна 2/6, или ⅓. В остальных случаях, когда у него выпадает двойка (4 раза из 6, то есть с вероятностью 4/6, или ⅔), мы всё равно можем проиграть, если у нас выпадет единица. Она у нас выпадает 3 раза из 6, то есть с вероятностью ½.
Чтобы посчитать общую вероятность победы соперника, надо сложить все вероятности отдельных побед:
⅓ (у него выпало 6) × 1 (вероятность того, что у нас будет 1 или 5);
+
⅔ (у него выпало 2) × ½ (у нас выпала единица);
=
⅓ + ⅓ = ⅔.
Получается, что если мы выберем кубик с пятёрками, а соперник — с шестёрками, то мы проиграем в ⅔ случаев. Тогда выбираем кубик с шестёрками?
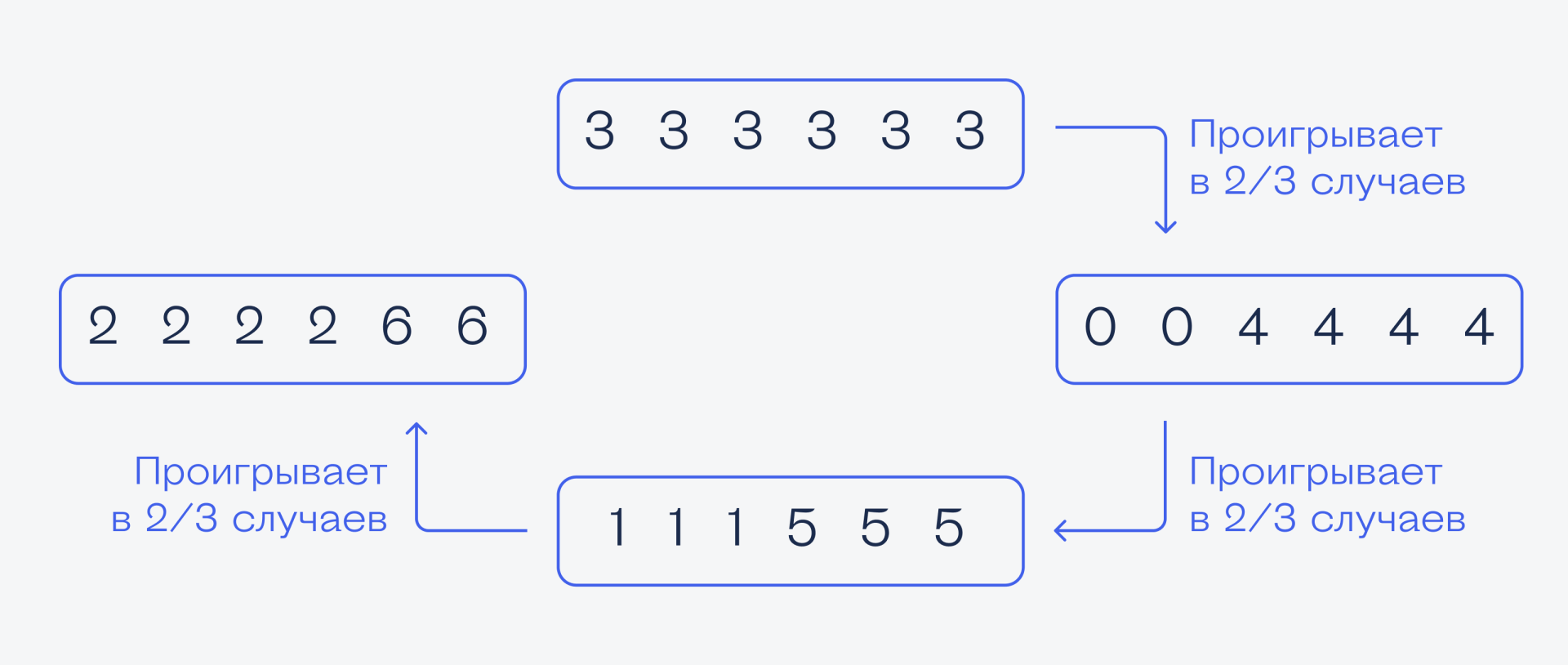
Шестёрки. Допустим, мы решили брать кубик с шестёрками. В этом случае соперник выберет кубик с тройками, и вот почему.
Соперник выиграет, только если у него выпадет 3 (а это будет всегда), если у нас будет двойка — а она выпадет с вероятностью 4/6 или ⅔. Получается, что если мы выберем кубик с шестёрками, а соперник — с тройками, то мы проиграем в ⅔ случаев. Тогда что нам выбрать?
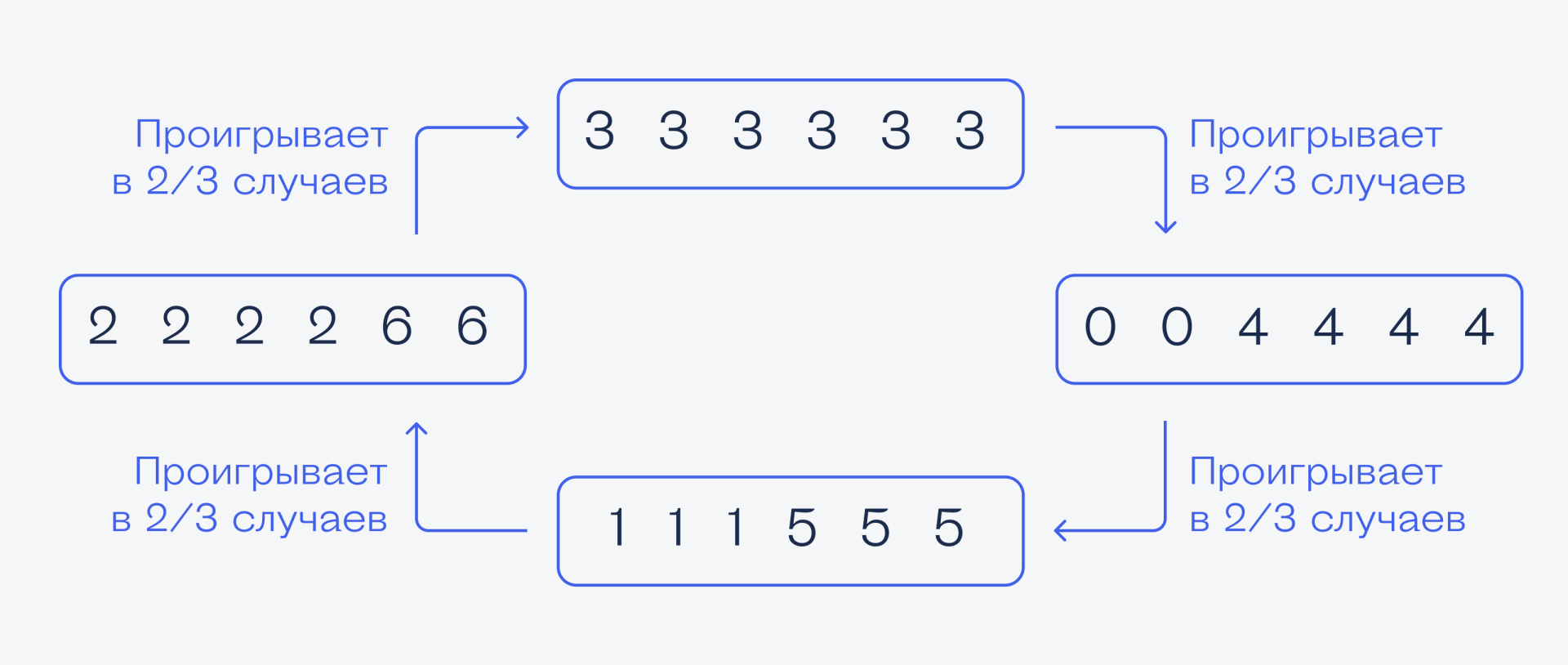
Какой вывод? Тот, кто выбирает кубик первым, всегда будет проигрывать после 1000 бросков, если соперник выберет тот кубик, который принесёт ему выигрыш в ⅔ случаев. Поэтому, какой бы кубик мы ни выбрали, если соперник не дурак, он нас обыграет.