Для многих логарифм — это самая странная часть в математике: непонятно, как их считать, где применять и как они могут пригодиться в жизни. Сегодня ответим на все эти вопросы.
Если интересно, как в математике работают остальные функции и символы, вот что у нас уже есть:
Что такое логарифм
Задача логарифма — ответить на такой вопрос:
В какую степень нужно возвести одно число, чтобы получилось другое?
На языке математики это будет выглядеть вот так:

Теперь сделаем то же самое, но уже с числами. Например, нам нужно узнать, в какую степень нужно возвести число 2, чтобы получить 8. Если вспомнить степени двойки, то будет ясно, что 2³ = 8, а значит, ответ будет «в третью степень». Мы только что нашли логарифм числа 8 по основанию 2.

Десятичный, натуральный и другие логарифмы
Число A, которое возводят в какую-то степень, называется основанием логарифма. Самые популярные у математиков логарифмы — десятичный и натуральный.
Десятичный логарифм — это когда в основании логарифма стоит число 10. Наша задача в этом случае — найти, в какую степень нужно возвести 10, чтобы получить желаемое число. Обозначается так — lg:

Натуральный логарифм устроен похоже, только вместо десятки в основании логарифма стоит число e, которое примерно равно 2,71828 и называется числом Эйлера. В математике число e играет такую же важную роль, как в геометрии — число пи, поэтому логарифм по основанию e часто встречается во многих математических выкладках и доказательствах.
Обозначается натуральный логарифм так — ln:
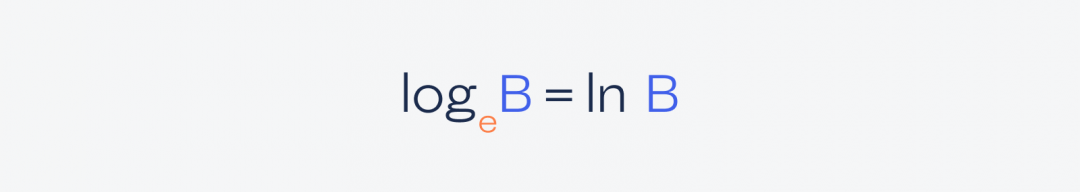
Логарифмическая шкала
Если мы возьмём линию и отметим на ней точки через каждый сантиметр, то мы получим арифметическую шкалу. Арифметическую — потому что каждая новая отметка считается арифметическим действием — сложением шага и предыдущего значения:
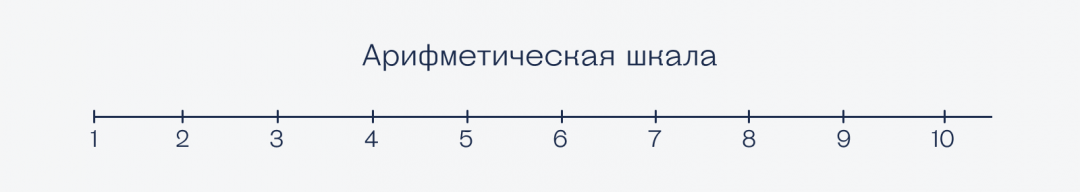
Но если мы вместо сложения возьмём логарифм, например, по основанию 10, то каждая новая отметка будет зависеть от значения десятичного логарифма:

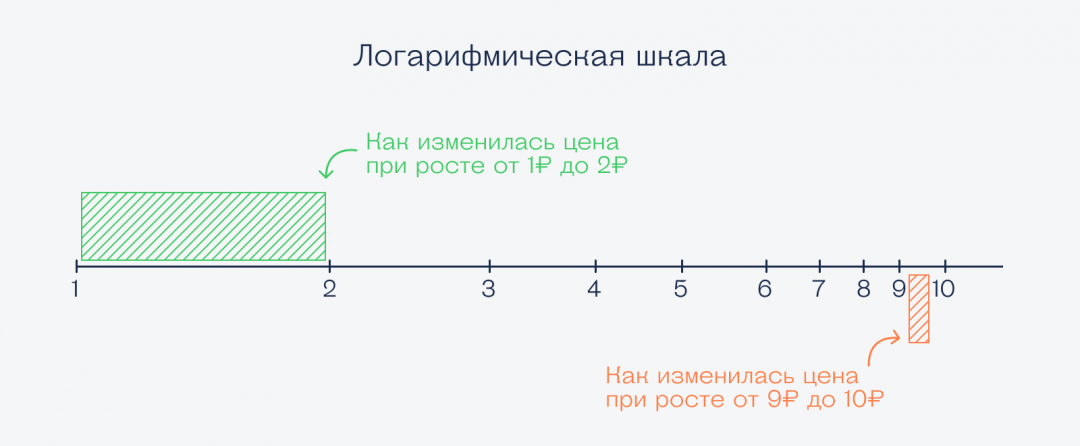
Это выглядит странно, но логарифмическая шкала постоянно применяется в экономике и маркетинге, когда нужно оценить рост или падение стоимости товара. Если взять обычную арифметическую шкалу, то разница между парами (1, 2) и (9, 10) будет одной и той же — 1 пункт.

Но при этом в первом случае цена выросла в 2 раза, с 1 до 2, а во втором случае — всего лишь на 10%. С логарифмической шкалой рост цены будет выглядеть логичнее:
Зачем нужны логарифмы в жизни
Вокруг нас и в быту мы встречаем гораздо больше логарифмов, чем кажется. Вот несколько примеров.
Децибелы, в которых измеряется относительная громкость любых звуков, считаются по десятичному логарифму. Относительная — потому что она считается от минимального порога громкости, которую только может расслышать человек. Например, если громкость звука равна 20 децибел, то это значит, что это громче самого тихого в 100 раз, а если 30 децибел — то в 1000 раз.
В химии активность водородных ионов тоже считается по логарифмической шкале.
Выдержки и диафрагмы в фотографии тоже меняются логарифмически — каждое новое значение больше или меньше предыдущего в определённое число раз.
В ракетостроении для вычисления скорости ракеты используется уравнение Циолковского. В основе этого уравнения — логарифмическая зависимость от массы ракеты с топливом и без него.
Логарифмы в природе
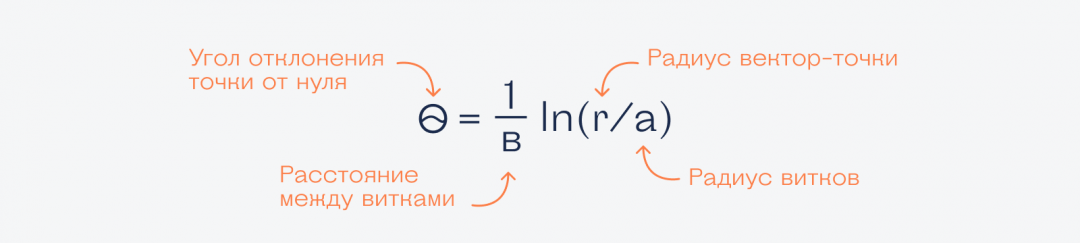
Больше всего логарифмов можно встретить в природе в виде логарифмической спирали. Математическая формула спирали выглядит так:
Если мы захотим построить график этого уравнения, то он будет выглядеть так:
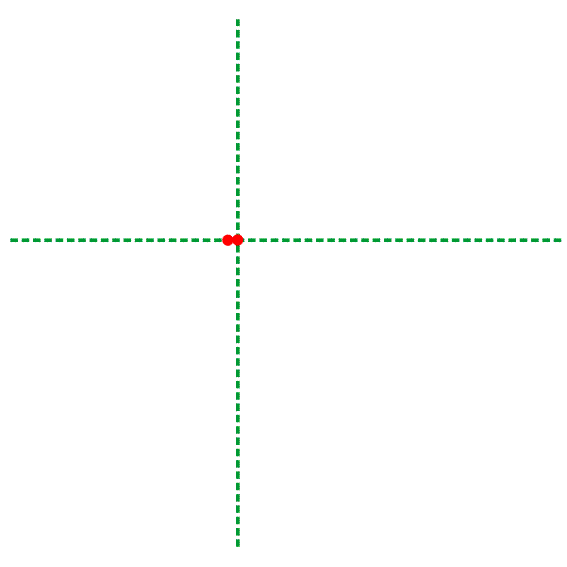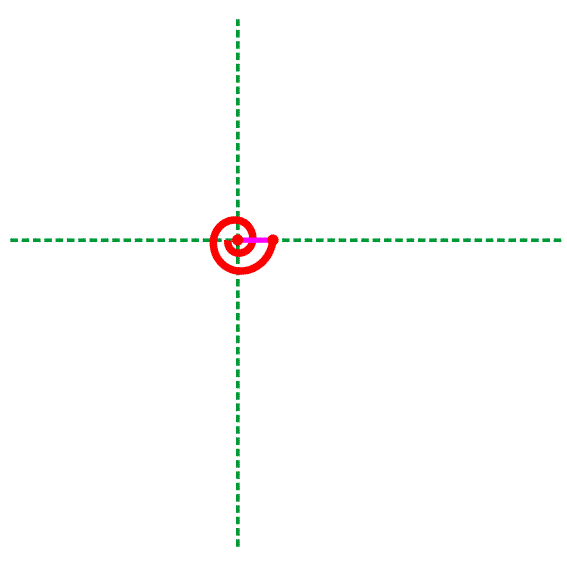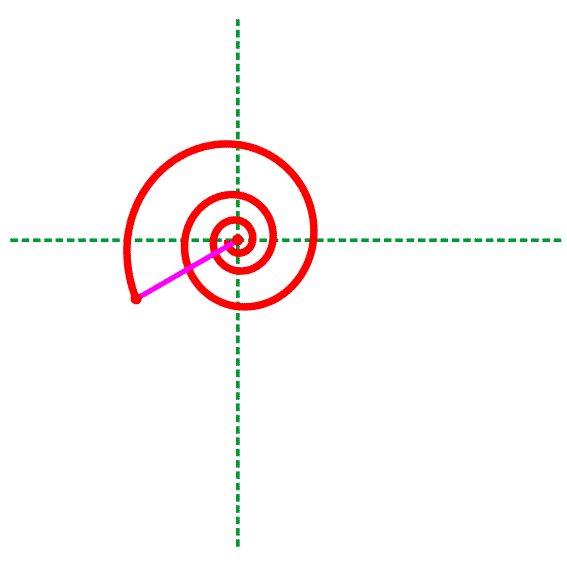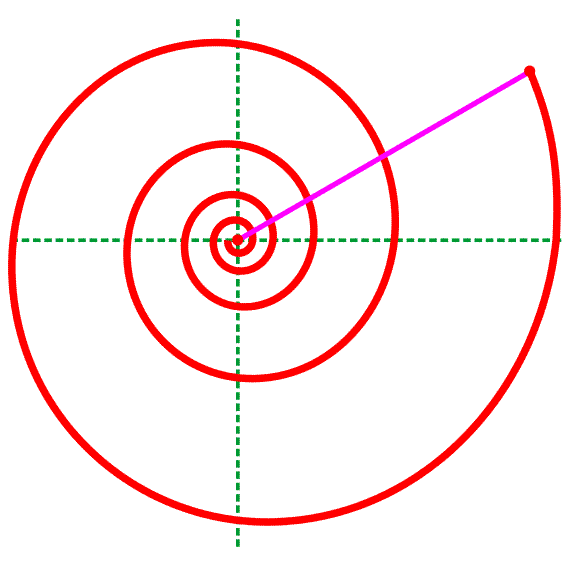
А вот логарифмическая спираль в природе — в ракушках, подсолнечнике и капусте. С капустой ещё связана другая интересная тема — фракталы, но про них поговорим в другой раз.



Даже рога у горных козлов закручиваются по логарифмической спирали:

Что дальше
Теперь мы знаем про логарифмы достаточно, чтобы понять, как они работают. В следующей статье напишем простую программу из двух циклов, которая посчитает нам практически любой логарифм по любому основанию.