Перед вами простой тест на то, нужен ли вам сейчас отдых. Если вы достаточно отдохнули, вы сможете решить эти задачи. А если не сможете, значит, вам нужно отдохнуть ещё — имеете полное право.
Который час
На шашлыках кто-то из компании спросил программиста, который час. Программист ответил: «Если бы сейчас было на два часа позже, то до полуночи оставалось бы в два раза меньше времени, чем если бы сейчас было на час позже. Который сейчас час?»
Если у вас не получится сразу решить эту задачу в уме, попробуйте письменно.
Раз наша задача — выяснить, который сейчас час, то обозначим текущее время за X, а всё остальное будем привязывать к этому иксу. Теперь переведём все данные, которые у нас есть из условия, на язык математики:
- Сейчас время X.
- Через два часа будет X + 2.
- До полуночи оставалось бы 24 − (X + 2).
- Через час будет X + 1.
- До полуночи в этом случае останется 24 − (X + 1).
- Число из п. 3 вдвое меньше, чем число из п. 5.
Запишем выражение из п. 6 в виде уравнения
24 − (X + 1) = (24 − (X + 2)) × 2
Нам осталось решить это уравнение и найти X — текущее время по условию задачи.
24 − (X + 1) = (24 − (X + 2)) × 2
👉 Поменяем местами для удобства
2 × (24 − (X + 2)) = 24 − (X + 1)
👉 Раскроем скобки справа и слева
48 − (2X + 4) = 24 − X − 1
48 − 2X − 4 = 23 − X
👉 Перекинем иксы налево, а числа направо
X − 2X = 23 + 4 — 48
👉 Ну теперь совсем легко
−X = −21
X = 21
Получается, что на часах сейчас 21:00.
Проверим это, подставив 21 в условие: если бы сейчас было на два часа позже, то было бы 23 часа и до полуночи остался бы час. Если бы было на час позже, было бы 22 часа и до полуночи остаётся ещё два часа — как раз в 2 раза больше времени. Всё сходится.
Странные часы
Многим понравилось отгадывать загадку программиста о том, который сейчас час, и его попросили загадать ещё одну.
Программист загадал: «Есть обычные настенные часы, но без цифр и без указания, где у них верх, а где низ. Все стрелки на часах одинаковые — секундная, минутная и часовая. Определите, какое время показывают эти часы, по их картинке».
После этого он взял салфетку и нарисовал на ней часы угольком из мангала. Мы покажем вам более аккуратный рисунок:
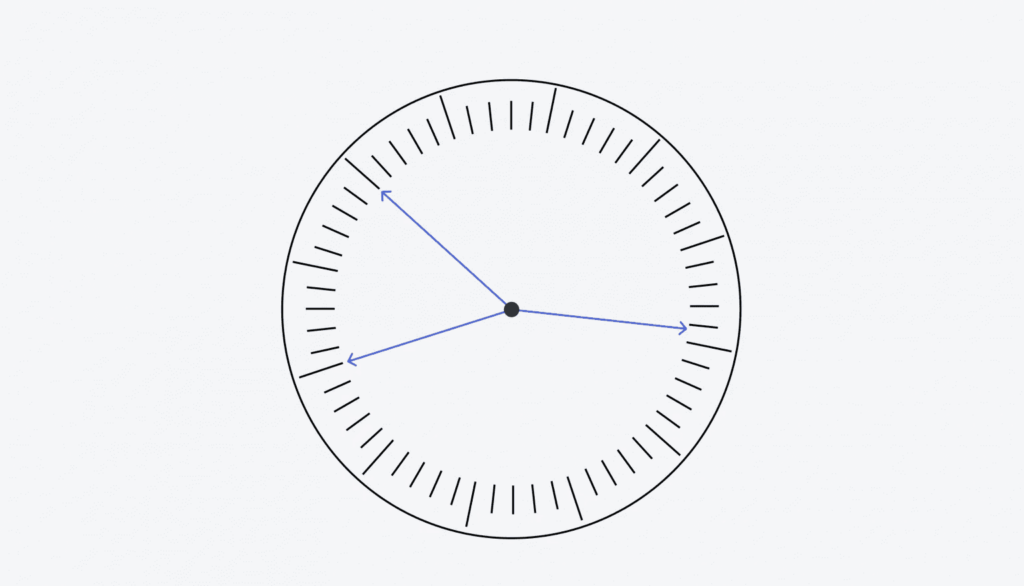
Компания задумалась, и тогда программист дал подсказки:
- Все стрелки двигаются плавно.
- Циферблат не отзеркален.
- Крупные риски показывают часы или пятиминутные отрезки.
- Решение опирается на то, как работают часы.
Сможете определить, какое время показывают часы?
Чтобы как-то отличать стрелки друг от друга, мы их подпишем — A, B и C:
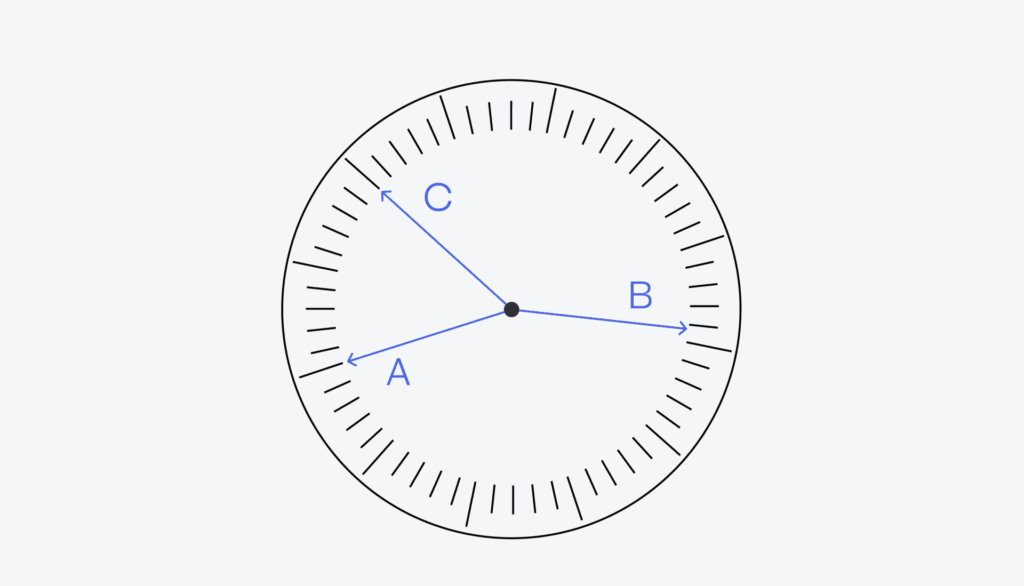
Теперь будем делать разные предположения, какая стрелка за что отвечает, а потом посмотрим, к чему это приведёт. Это, кстати, один из вариантов решения любых сложных задач: сформулировать какую-то гипотезу, принять её за правильный ответ и посмотреть, а бьётся ли задача с этим предположением.
Гипотеза: часовая стрелка — A или C. Стрелки A и C указывают точно на часовые (или пятиминутные) отметки. Если бы одна из этих стрелок была часовой (показывала часы), то обе оставшихся стрелки указывали бы ровно на отметку в 12 часов. А всё потому, что часовая стрелка указывает точно на свой час только в тот момент, когда минутная и секундная указывают на 12.
Раз у нас ни одна стрелка не совпадает по расположению с другой, значит, наша гипотеза неверна и ни A, ни C — не часовые стрелки. А раз так, значит, остаётся единственная часовая стрелка — это B.
Вывод: B — часовая стрелка.
Раз обе эти стрелки указывают точно на часовые отметки, значит, секундная направлена точно на 12 часов, а минутная — на какую-то только что наступившую минуту.
Теперь получается два варианта:
- A — секундная, C — минутная стрелка.
- С — секундная, А — минутная стрелка.
Возьмём первый вариант как новую рабочую гипотезу (A — секундная, C — минутная). Раз A — секундная и показывает точно на 12, то мы можем оттолкнуться от этого и пронумеровать все остальные деления на часах:
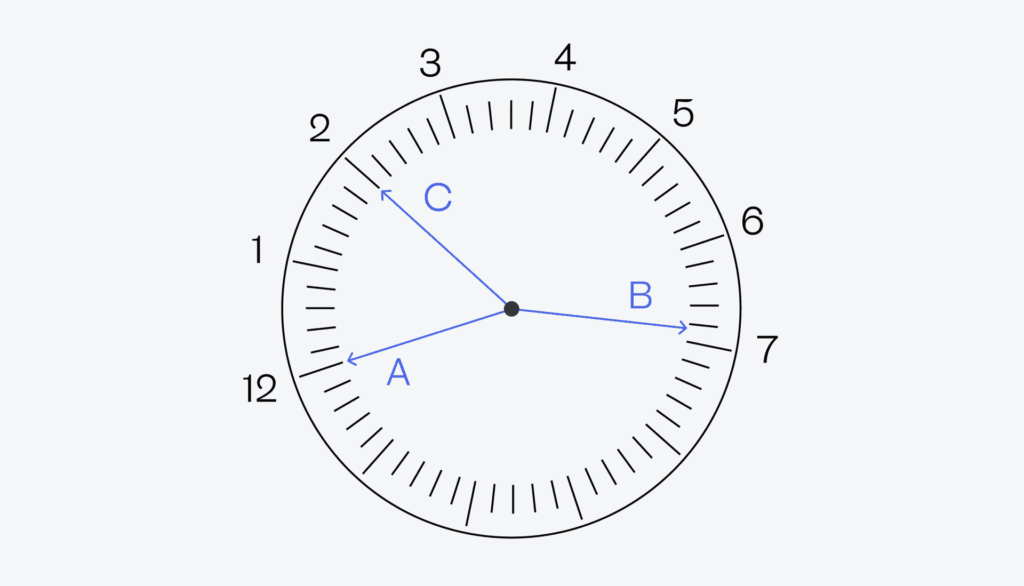
Но раз так, то минутная © показывает, что прошло 10 минут с начала часа, а часовая (B) — что час вот-вот закончится. Так не бывает в нормальных часах, поэтому этот вариант мы отбрасываем.
Новая гипотеза: С — секундная, А — минутная стрелка. Рассмотрим второй вариант, когда секундная стрелка — это С, и она указывает точно на 12. Отталкиваясь от этого, пронумеруем остальной циферблат и посмотрим, что получилось:
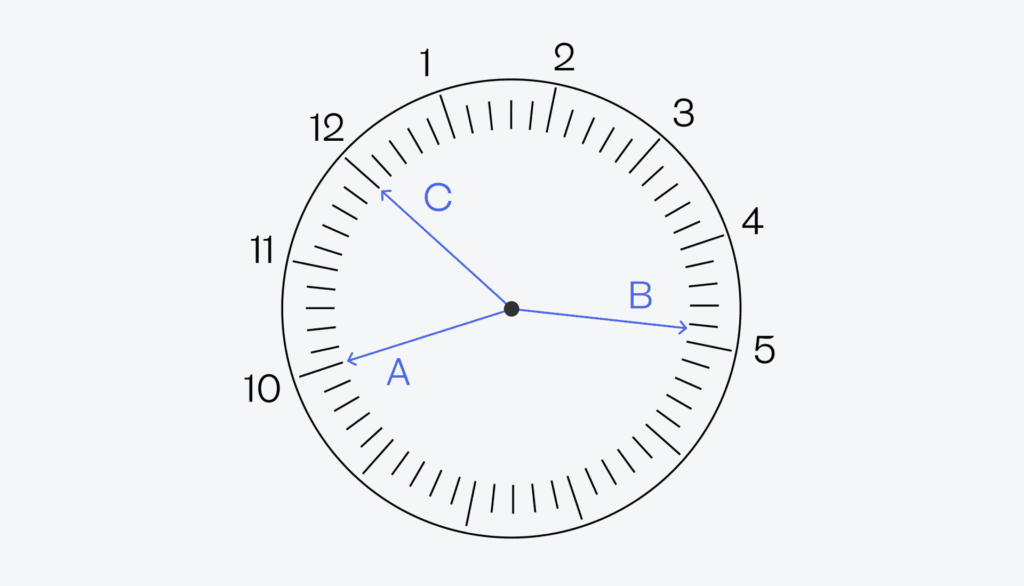
Минутная стрелка у нас указывает теперь на 10 — это значит, что до конца часа осталось 10 минут. Посмотрим на часовую стрелку: она почти дошла до пятёрки, а значит, до конца часа осталось совсем немного, например те же 10 минут. Кажется, мы нашли правильный ответ. Чтобы в этом убедиться, перевернём циферблат правильно:
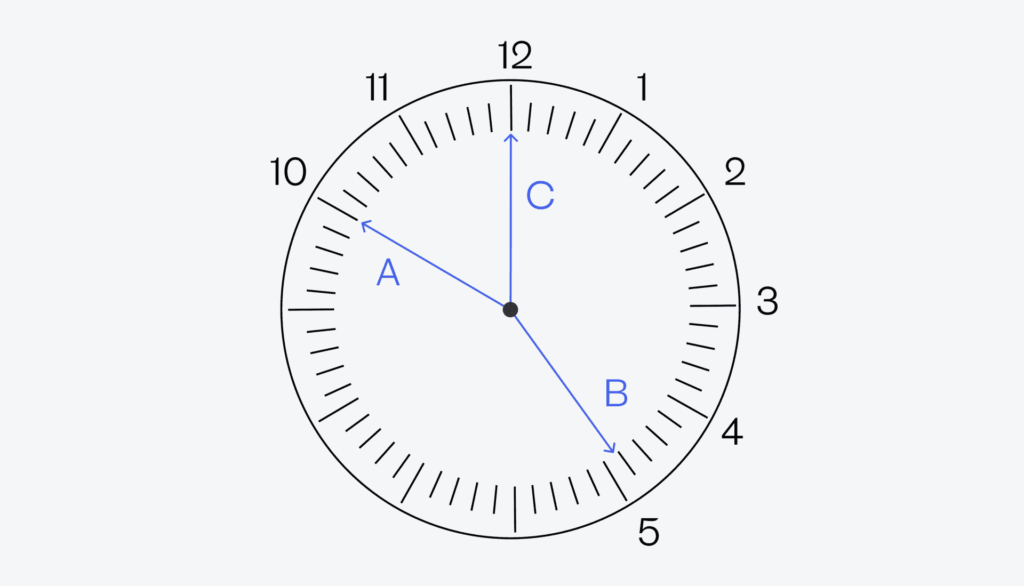
Получается, что часы показывают 4:50 или 16:50.
 Коктейльная задача про доли и крепость
Коктейльная задача про доли и крепость Задача про программистов и угощение в баре
Задача про программистов и угощение в баре Задача про гору и альпинистов-программистов
Задача про гору и альпинистов-программистов Задача про тренера и каратиста
Задача про тренера и каратиста Задача про шаблонное мышление
Задача про шаблонное мышление Лучшие задачи, где потребуется нестандартное мышление
Лучшие задачи, где потребуется нестандартное мышление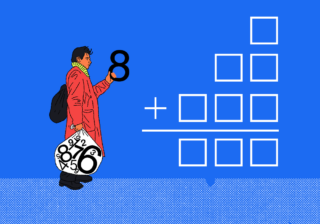 Простая школьная задача про числа, с которой иногда не могут справиться взрослые
Простая школьная задача про числа, с которой иногда не могут справиться взрослыеВода в бутылке
Среди собравшихся был ещё один программист, и он решил загадать свою загадку:
— Есть стеклянная бутылка на 900 миллилитров, в ней сколько-то воды. У нас есть линейка. Как понять, сколько в бутылке воды?
— Дай мне больше данных.
— Предположим, что при измерении мы получаем вот такие параметры:
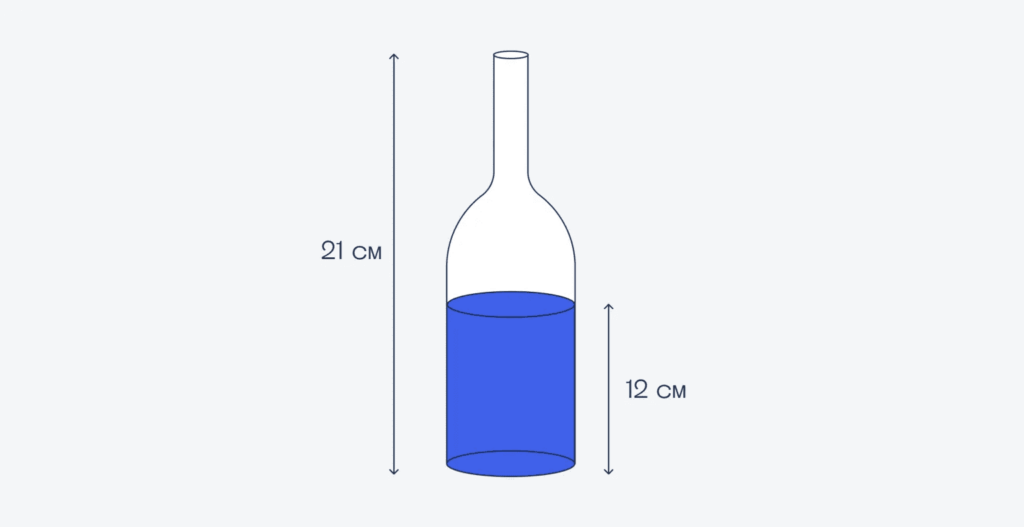
— Мне нужны ещё данные.
— Если перевернуть бутылку, то получатся такие измерения:
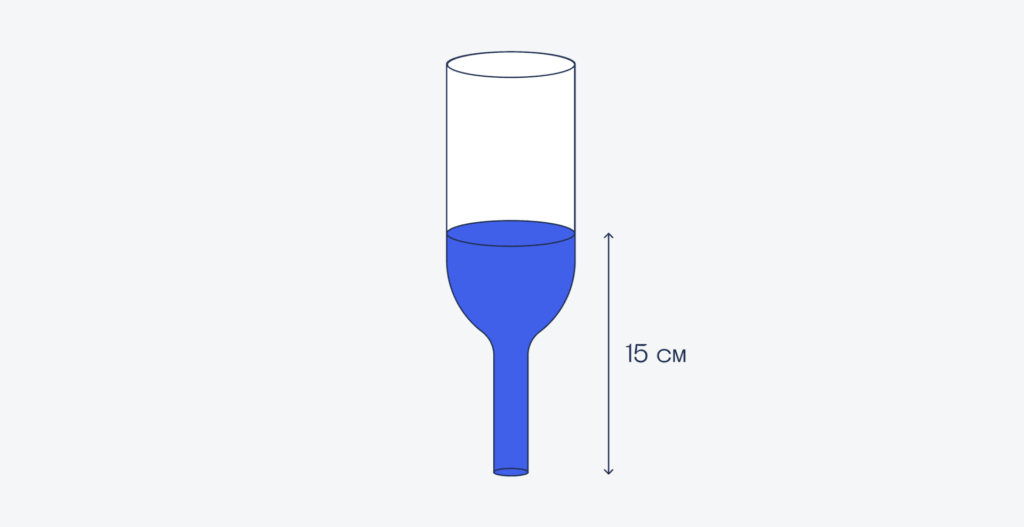
И тут, к удивлению всей компании, первый программист определил, сколько воды в бутылке. Как он это сделал?
Ключ к решению — пустое пространство в бутылке, которое в ней есть при любом положении. Объём воздуха в бутылке одинаковый при обычном и перевёрнутом положении:
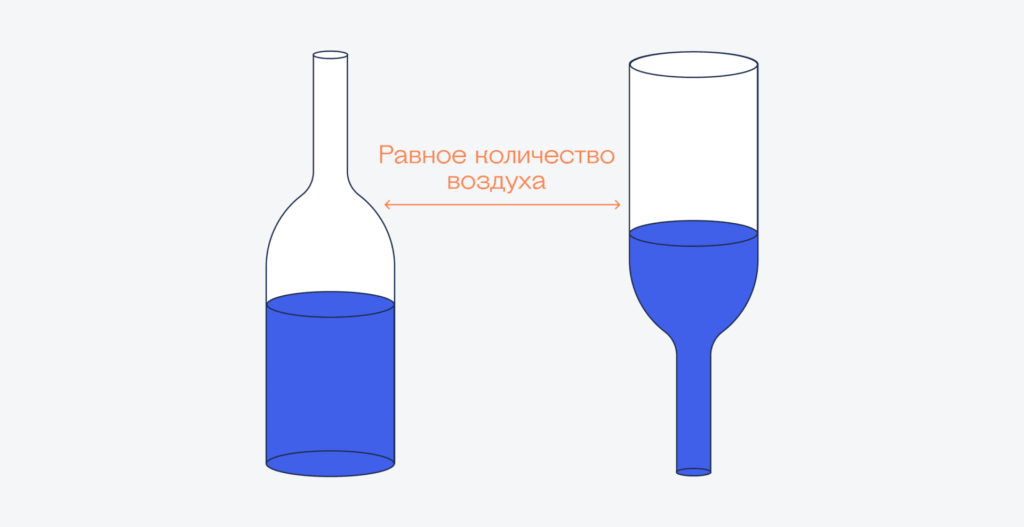
Это значит, что мы можем измерить высоту воздушного пространства, чтобы потом сравнить с высотой воды в обычном положении бутылки. Дело в том, что радиус ёмкости в этом случае будет одинаковый, а значит, единственная характеристика, которая влияет на объём, — это высота:
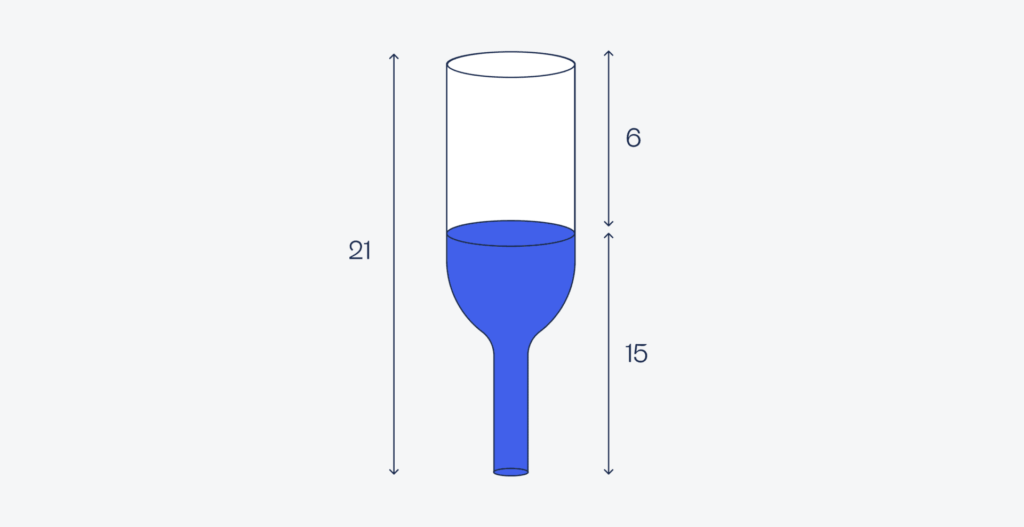
В итоге получается, что у нас есть цилиндр воды с высотой 12 сантиметров (на первой картинке) и цилиндр воздуха с высотой 6 сантиметров. Площадь круга в основании у них одинаковая и равна πR², где R — это радиус.
Получается, что бутылка заполнена водой на 12 × πR², а общий объём бутылки — это (12 + 6) × πR². Разделим одно на другое, чтобы понять, сколько там частей воды:
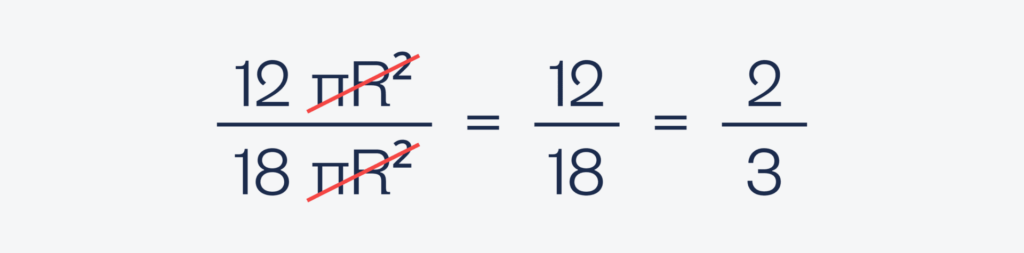
Выходит, что воды в бутылке — ровно ⅔. Но по условию весь объём бутылки — это 900 миллилитров, а значит, воды в ней — 900 × ⅔ = 600 миллилитров.
Спор двух программистов
Первый программист сказал второму:
— Загадай любое натуральное число X!
— Ну загадал.
— А теперь придумай три любых числа от 6 до 8 включительно.
— Придумал, и что дальше?
— А теперь умножь своё начальное число X на первое из них, прибавь второе и отними третье. Сколько у тебя получилось?
— Минутку… 164.
— Ха, а я знаю, какие ты числа загадал!
— Что, все четыре числа вычислил?!
— Ага!
— НО КАК?!
Действительно, как первому программисту удалось узнать все числа, которые загадал второй?
Обозначим три загаданных числа от 6 до 8 как A, B и C. Если мы сделаем всё, как написано в задаче, то получим равенство: A × X + B − C = 164.
Из этого получим X:
X = (164 − B + C) / A
Исключаем число 7
Если A = 7, то числитель нашей дроби должен нацело делиться на 7, потому что X не может быть дробным (по условию X — натуральное число). Числа, близкие к 164, которые делятся на 7 — это 161 и 168.
Чтобы получить 161 в числителе, числа B и C должны отличаться друг от друга на 3, а это невозможно, потому что максимальная разница равна 8 − 6 = 2.
Чтобы получить 168 в числителе, числа B и C должны отличаться друг от друга на 4, а это тоже невозможно, потому что максимальная разница равна 8 − 6 = 2.
Значит, A точно не равно 7. Запомним это.
Если число A точно не 7, то оно чётное — 6 или 8. Это значит, что числитель (164 − B + C) тоже чётный, чтобы в результате деления получилось целое число. А это возможно, если числа B и C оба чётные или оба нечётные.
Если числа B и C оба нечётные, то это возможно только в случае, если они оба равны 7. В этом случае −B + C = 0, и в числителе остаётся только 164, которое нам предстоит разделить на 6 или 8. Но 164 не делится нацело ни на 6, ни на 8, значит, они тоже не равны 7.
Исключаем одинаковые B и C
Из последнего примера мы видели, что B и С не могут быть одинаковыми в принципе, неважно, чётными или нечётными, поэтому остаются только два варианта:
B = 6, C = 8 или B = 8, C = 6.
Проверяем оставшиеся варианты
Если B = 6 и C = 8, то в числителе получается так: (164 — 6 + 8) = 166. Но 166 не делится нацело ни на 6, ни на 8 (возможные значения A), значит, этот вариант можно исключить.
Получается, что остаётся только пара B = 8 и C = 6: (164 — 8 + 6) = 162. Число 162 нацело делится только на 6: 162 / 6 = 27, значит, A = 6, а второй программист загадал число 27:
X = 27
A = 6
B = 8
C = 6
Проверяем: 6 × 27 + 8 − 6 = 164. Всё сходится.
Киоск с пончиками, брецелями, пиццей и мороженым
Рядом с местом, где отдыхала компания, был киоск, в котором продавали пончики, брецели, пиццу и мороженое. В компании отдыхающих был начинающий маркетолог, который на протяжении дня с интересом наблюдал за посетителями киоска и к вечеру собрал такую статистику:
- пончики покупают 65% посетителей;
- брецели — 80%;
- пиццу — 80%;
- мороженое — 90%.
Начинающий маркетолог понял, что как минимум 65% посетителей покупают все эти продукты, и сказал, что киоск мог бы увеличить выручку, если бы продавал набор из всех четырёх компонентов. Но программист сказал, что на самом деле таких покупателей меньше, и доказал это за 5 минут.
Так сколько людей покупают все 4 перекуса?
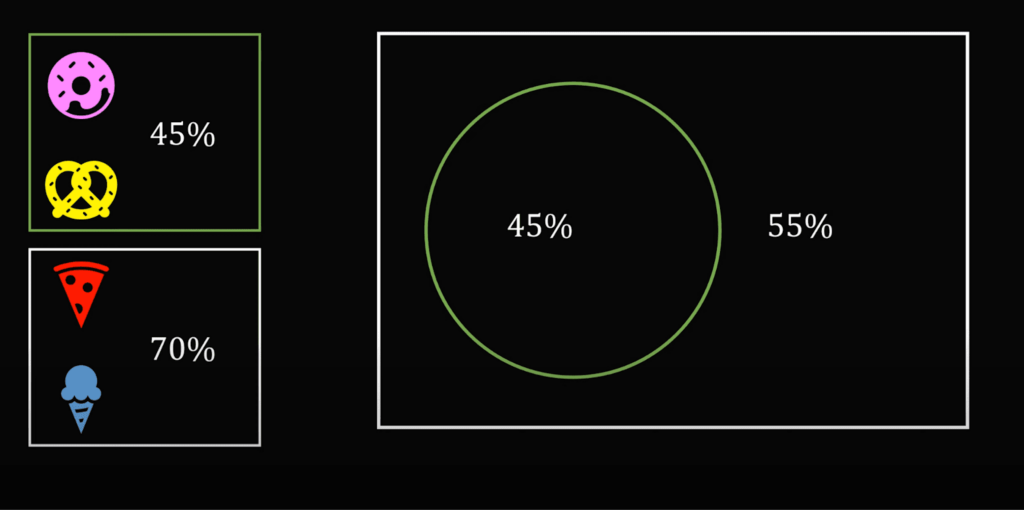
Чтобы было проще, нарисуем кружочками процентное соотношение всех, кто покупал перекусы. Один кружочек — 5%:

Начинающий маркетолог думал так: раз 65% покупателей — это минимальное количество среди всех покупателей, то это значит, что эти же 65% точно покупают все 4 перекуса:

Но на самом деле это не так. Чтобы выяснить реальное количество таких покупателей, нам нужно рассмотреть самый негативный сценарий — когда покупатели максимально не пересекаются по продуктам.
Начнём с брецелей: возьмём 20% тех, кто их не покупает, и сдвинем влево так, чтобы они закончились ровно под теми кружочками, которые не покупают пончики. Для этого берём этих покупателей…

…и сдвигаем их левее, чтобы они заканчивались там, где заканчиваются покупатели пончиков:

То же самое сделаем с пиццей — передвинем серые кружки левее, чтобы они закончились там, где начинаются серые у брецелей:

И, наконец, проделаем это с мороженым:

Теперь посмотрим на процент тех, кто гарантированно покупает все 4 продукта — это всего первые три кружка, то есть 15%:

Второй способ решения — использовать круги Эйлера (осторожно, Википедия). С их помощью мы сможем найти пересечения между разными группами покупателей и найти тех, кто берёт все продукты.
Начнём с пары «пончик — брецель». Мы знаем, что пончики покупают 65% посетителей — это значит, что 35% их не берут:
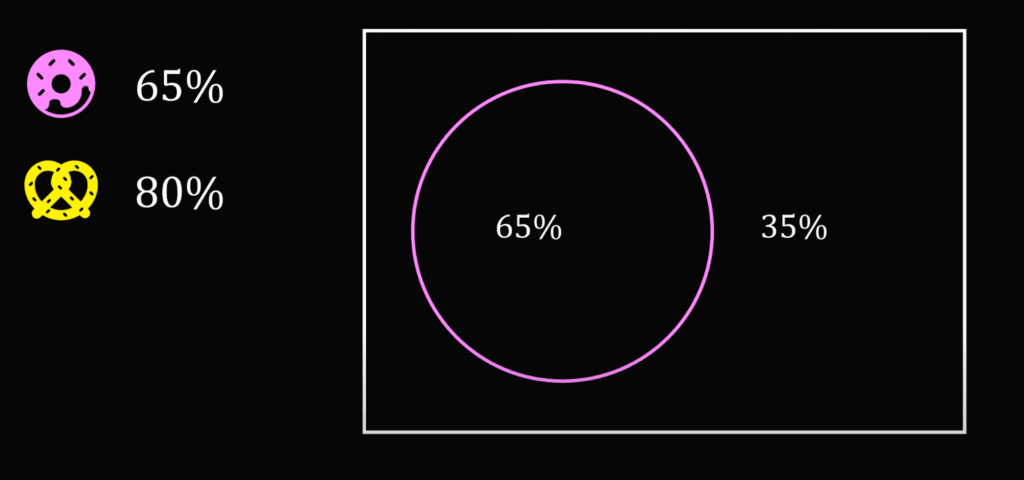
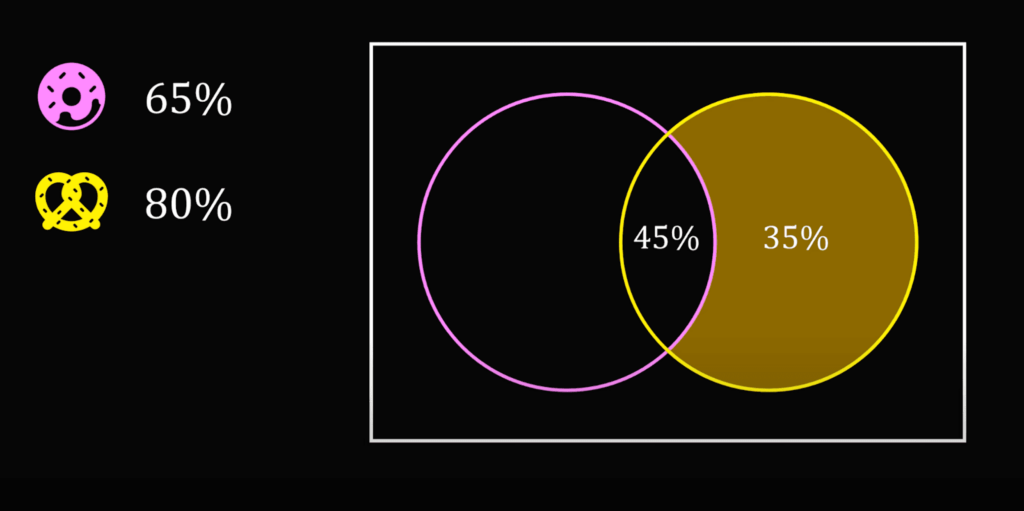
Эти 35% могут также не входить в число тех, кто берёт брецели, — исходим из этого, чтобы найти минимально возможное пересечение. Получается, что раз 80% посетителей берут брецели и 35% из них не берут пончики, то в этой паре только 45% посетителей берут и то и другое:
Теперь сделаем то же самое с парой «пицца — мороженое». Если 80% берут пиццу, то 20% её не покупают:
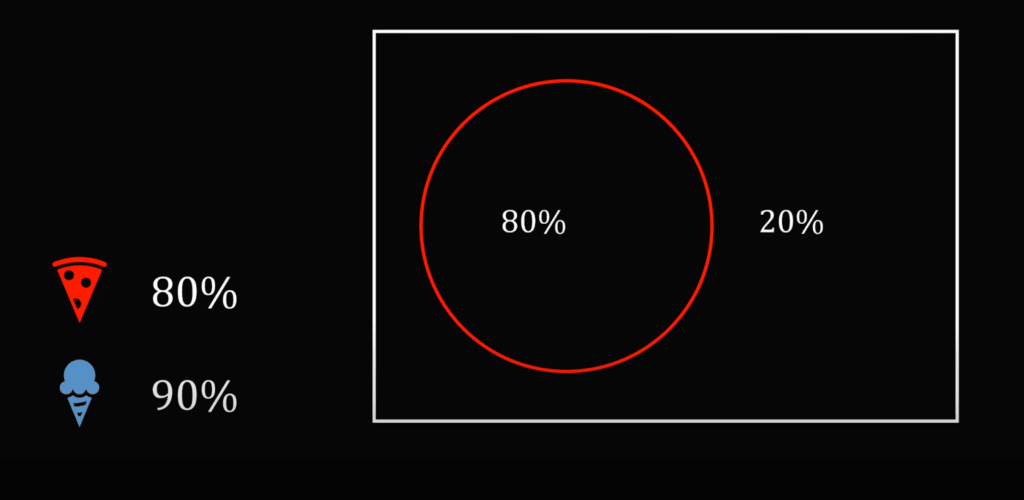
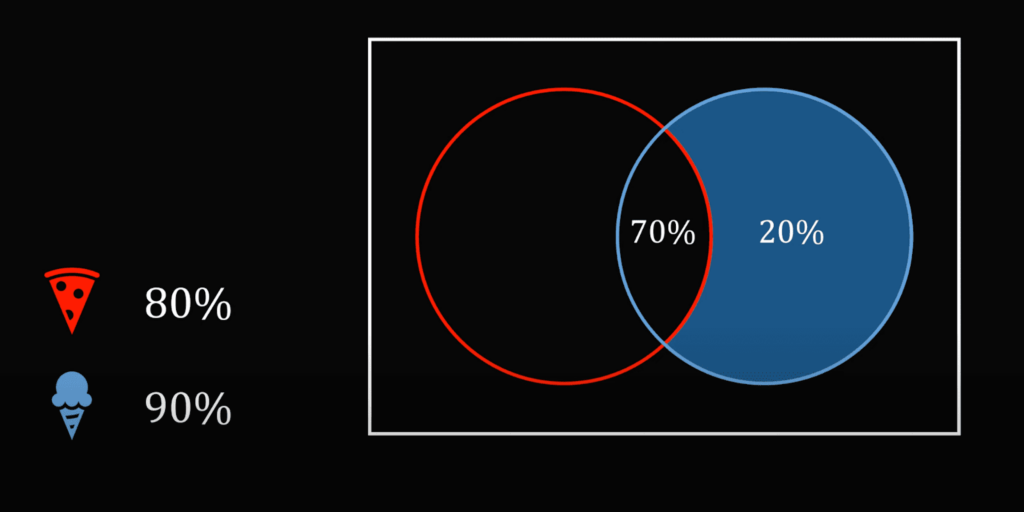
Соответственно, из 90% тех, кто берёт мороженое, 20% не берут пиццу. Значит, тех, кто покупает и пиццу, и мороженое, — 90% − 20% = 70%:
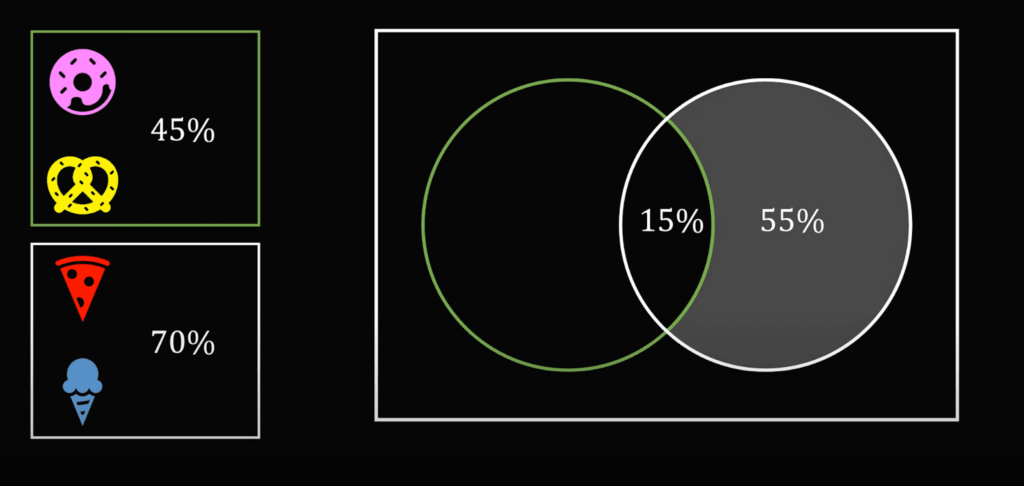
Наконец, объединим эти две группы в одну, чтобы найти общее пересечение — тех, кто покупает все четыре продукта. Для этого сделаем то же самое: если пончик и брецели берут 45%, то 55% покупателей их не берут:
Добавим сюда тех, кто берёт пиццу и мороженое, — их 70%. А раз 55% не берут пончик и брецель, получается, что тех, кто берёт все четыре продукта, — 70% − 55% = 15%:
Используем матлогику для решения. Чтобы найти размер пересечения двух множеств, используется такая формула:
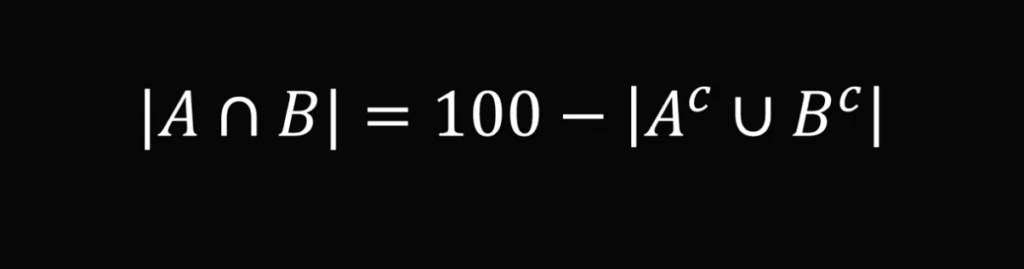
В переводе на русский это значит: чтобы найти процентное пересечение двух множеств, нужно от ста отнять объединение дополнений этих множеств. Дополнение — это то количество, которое не хватает множеству до 100%.
Например, для пересечения пончиков и брецелей это работает так:
100% − (35% [не хватает пончикам до сотни] + 20% [не хватает брецелям до сотни]);
100% − 55% = 45% — именно такой результат мы получили в решении с кругами.
Обозначим буквами все продукты:

Теперь используем ту же формулу, чтобы посчитать общее пересечение четырёх множеств:
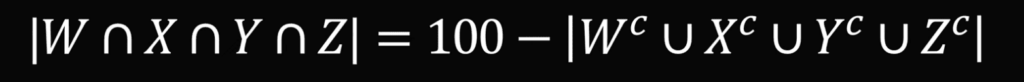
Подставим цифры вместо дополнений и раскроем скобки:
100 − 35 − 20 − 20 − 10 = 15
Получается, что эти множества пересекаются как минимум на 15%, а это значит, что реальных покупателей, которые берут все четыре продукта, — 15%.
Поиски потерянного мангала
После отдыха все начали разъезжаться. Кто-то из компании обнаружил, что его мангал увезли. Разработчика, который был с самого начала, попросили выяснить, в какой машине могли увезти мангал. Программист опросил тех, кто помогал собирать мангал, в какую машину его положили, но все говорили разные вещи:
- Первый утверждал, что это были синие «Жигули».
- Второй — что это чёрная «Тойота».
- Третий вообще сказал, что это был «Опель», но точно не синий.
Программисту показалось странным такое несоответствие, и он опросил народ ещё раз. Выяснилось, что каждый из помогавших собирать потерянный мангал сомневается в марке или цвете. Все думали, что найти машину не получится, но программист смог вычислить, на какой машине увезли мангал.
Как он это сделал?
Эта задача решается простым алгоритмом с элементами перебора: берём высказывание первого свидетеля, предполагаем, что первая часть верная, а вторая — нет. После этого проверяем, насколько это совпадает с остальными условиями задачи и высказываниями остальных свидетелей.
1-й вариант: допустим, первый «свидетель» был уверен в цвете, но сомневался в марке автомобиля. Получается, что цвет машины — синий, и это точно не «Жигули».
Тогда второй «свидетель», который сказал про чёрную тойоту, сомневается в цвете, а это значит, что он уверен в марке. Получается, что машина была — синяя «Тойота».
Теперь проверим показания третьего «свидетеля». Он тоже сомневается в своих наблюдениях, но его ответ был — «точно не синий „Опель“». Выходит, что он сомневается и в цвете, и в марке.
Получается, что первый «свидетель» ошибся в цвете, а значит, про марку он сказал правду. Проверим это.
2-й вариант: допустим, первый «свидетель» не ошибается про марку — «Жигули», но сомневается в цвете. Получается, что у нас есть «Жигули» точно не синего цвета.
Второй «свидетель» сказал, что это была чёрная «Тойота», но мы уже поняли, что это были «Жигули», а значит, второй ошибается в марке и говорит правду про цвет. А цвет у второго «свидетеля» — чёрный. Получились чёрные «Жигули». Проверим показания третьего.
Третий «свидетель» сказал, что это был «точно не синий „Опель“», но мы-то уже знаем про «Жигули», поэтому третий с маркой тоже ошибается. А про цвет он как раз сказал правду: не синий — это тоже может быть чёрный.
Всё сходится — потерянный мангал увезли на чёрных «Жигулях».











