Задача про бабушку и домашний изюм
В самом начале работы журнала «Код» у нас вышла задача про бабушку и домашние помидоры. Прошло два года, бабушка расширила фермерское хозяйство и решила делать изюм из домашнего винограда.
В бабушкином винограде 92% воды, а в изюме после сушки на печке — 6% воды.
Вопрос: сколько килограммов винограда нужно вырастить бабушке, чтобы продать 100 килограммов изюма?
В этой задаче решение простое, но в нём всё равно можно запутаться. Следите за мыслью.
Если в изюме всего 6% воды, то в 100 килограммах изюма воды будет 6 килограмм (100 × 0,06 = 6), а сухого вещества — 94 килограмма (100 − 6 = 94).
Так как в винограде воды 92%, то сухого вещества в нём будет всего 8%, потому что в сумме должно получиться 100% (это виноград и с водой, и с мякотью).
Раз в винограде сухого вещества 8%, а бабушке нужно получить изюм с массой сухого вещества 94 килограмма, то и в винограде сухого вещества должно быть столько же. Это значит, что 8% составляют 94 килограмма, а 100% будет считаться так:
(94 / 8) × 100 = 11,75 × 100 = 1175 килограмм
Получается, что бабушке нужно будет вырастить и собрать больше тонны винограда, чтобы получить 100 кило изюма. Зная современных бабушек, мы ничего не исключаем.
Задача про математику и гендерное равенство
У нас была подобная задача про мальчика и двух девочек. Настало время исправить гендерный дисбаланс и дать всем равные права.
У одной девушки было два друга, они жили в противоположных концах города — на севере и юге. Девушка жила в центре. Каждый вечер она спускалась в метро и садилась на первый приходящий поезд. В какую сторону поедет поезд — к тому парню она и ехала.
Количество поездов в каждую сторону одинаковое, но девушка стала замечать, что в какое бы время она ни выходила из дома, к северному парню она приезжала в три раза чаще, чем к тому, что жил на юге. Она поняла, что это её судьба.
А действительно ли это судьба или она тут ни при чём? Почему так произошло?
Допустим, поезд отходит каждые две минуты с каждой платформы без перерывов — для чистоты эксперимента допустим также, что у нас круглосуточное метро. А дальше всё дело в интервалах между отправлениями с разных платформ.
Первый поезд на север у нас будет отходить в начале каждого целого двухминутного отрезка: в 0 минут, 2 минуты, 4 минуты и так далее. Запишем время отправления в минутах и секундах:
0:00
2:00
4:00…
А вот поезд на юг пусть отходит со смещением в 30 секунд относительно северного:
0:30
2:30
4:30…
И там и там интервал между поездами в одном направлении одинаковый — 2 минуты. Но получается, что после того, как ушёл поезд на север, у девушки есть всего 30 секунд, чтобы дождаться поезда на юг, если она не успела на первый. А вот потом у неё будет целых полторы минуты после отправления южного, чтобы уехать на север!
Это значит, что если девушка каждый раз случайно приходит на станцию, то она должна попасть в 30-секундный интервал, чтобы уехать на юг, или попасть в 90-секундный интервал, чтобы уехать на север. А раз второй интервал в 3 раза больше первого, то и попадать в него и уезжать на север девушка будет в 3 раза чаще.
Иногда судьба — это простая математика. И математике плевать, с каким гендером ты себя идентифицируешь сегодня.
Задача про девопсов и обед
👉 Предисловие к задаче: девопс — это такой айтишник, который следит за тем, чтобы у программистов и других разработчиков на компьютере работало всё, что нужно для работы. Если нужны подробности — читайте нашу статью про девопсов.
Теперь сама задача.
Один девопс пришёл к 9 утра на работу и стал настраивать компьютеры и софт в новом большом отделе. На эту задачу у девопса было запланировано 8 часов. В 11:00 к нему пришёл напарник:
— Пошли в 13:00 на обед в новое кафе, у них сегодня открытие и большие скидки, тут недалеко!
— Не смогу — занят работой.
— А давай я тебе помогу! Будем работать одновременно, сделаем всё быстрее и успеем на обед.
— Ну давай попробуем, кажется, тогда должны успеть.
Получится у них попасть на открытие нового кафе с большими скидками или ребята не успеют закончить работу к 13:00? Если сможете решить эту задачу в уме, без листочка — напишите в комментариях. Мы не смогли.
Чтобы узнать, успеют они или нет, нужно посчитать время, которое им понадобится, чтобы закончить работу.
На эту задачу у девопса уходит 8 часов, значит, за один час он делает 1/8 часть задачи. Получается, что первый девопс за 2 часа, пока работал один, успел выполнить 2 × 1/8 = 2/8 = 1/4 задачи. Запомним это.
Когда к нему присоединился коллега-девопс, то в час каждый из них выполнял по ⅛ задачи, а вместе они выполняли в час 2 × 1/8 = 2/8 = 1/4 задачи.
Обозначим за X то время, когда оба девопса работали над задачей одновременно. Получается, за X часов они выполнили (X × 1/4 ) часть задачи.
Получается:
первый девопс за 2 часа сделал 1/4 задачи;
потом вместе со вторым они доделали (X × 1/4 ) частей задачи за X часов.
Так как все части задачи вместе дадут единицу — полностью выполненную задачу, — то получаем такое уравнение:
¼ + X × ¼ = 1
Умножаем обе части на 4 и решаем уравнение до конца:
1 + X = 4 → X = 3
Это значит, что, чтобы справиться с работой вдвоем, им потребуется 3 часа. Сейчас 11:00. Значит, они управятся к 14:00 и к 13:00 не успеют.
Но с другой стороны — что им мешает сделать перерыв в 12:30, спокойно сходить на обед, вернуться и доделать?
Два аналитика, два неизвестных, две минуты
Нерадивый эйчар получил задание прособеседовать двоих кандидатов на должность аналитика. Он случайно назначил две встречи на одно время, кандидаты пришли. Ну и глупо: не будешь же ты их собеседовать одновременно.
Эйчар сделал вид, что всё так и задумано, и предложил кандидатам интеллектуальный поединок. Он быстро на бумажке что-то посчитал, а потом сказал:
- Предлагаю вам решить вот это уравнение с двумя неизвестными.
- Неизвестные m и n — целые положительные числа.
- Кто даст правильный ответ первым, тот проходит на следующий этап собеседования.
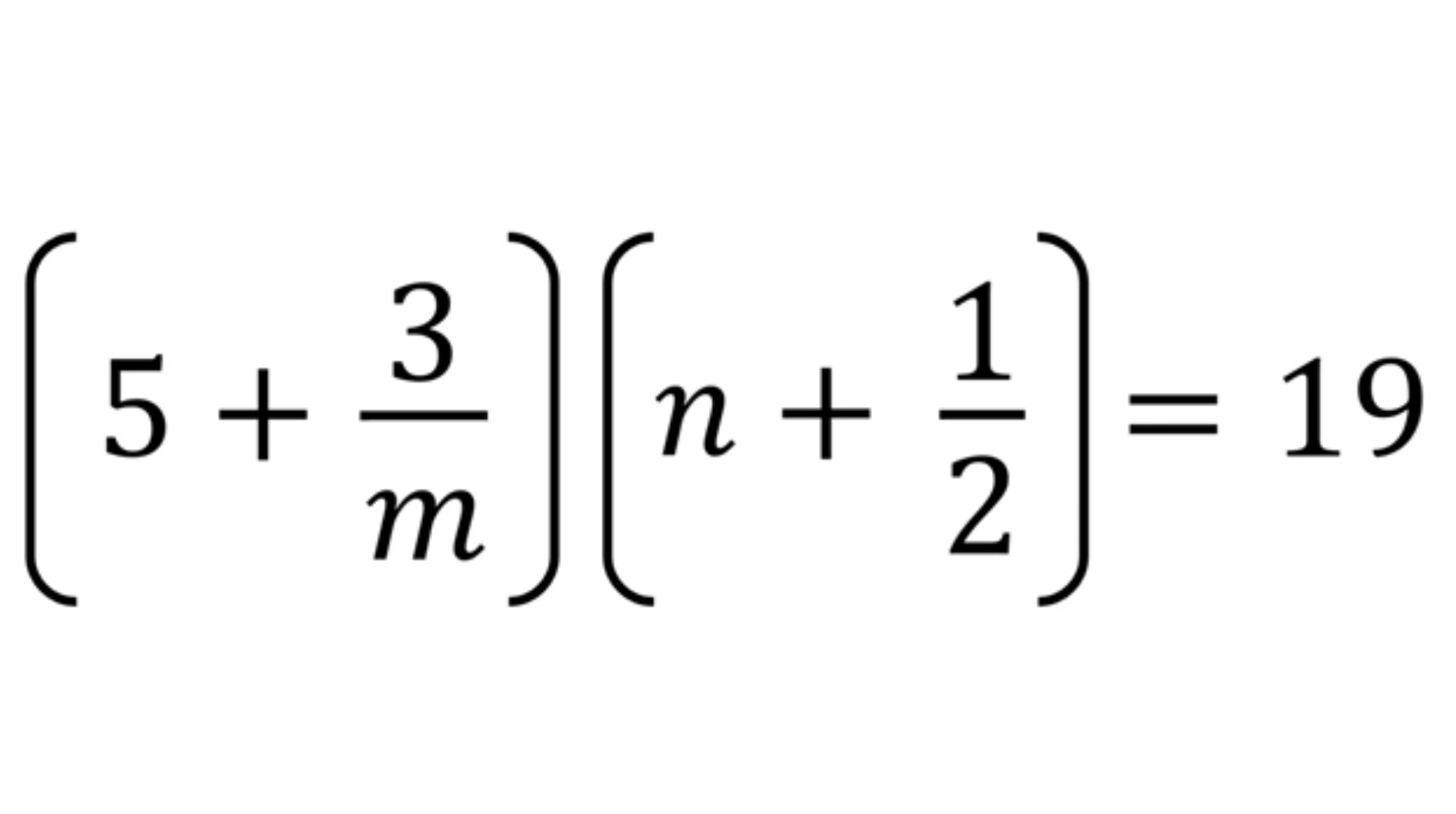
Один аналитик решил блеснуть своими навыками автоматизации. Он открыл ноутбук и стал писать программу, которая мгновенно нашла бы нужные корни.
А второй закатил глаза, написал на листке ответ, отдал его эйчару и красиво ушёл. И вот эйчар сидит и не понимает, как второму это удалось. А правда, как?
Есть два стандартных подхода к решению этого уравнения: алгебраическое и через сравнения соотношений. Оба требуют обстоятельных разъяснений каждого действия.
Но есть и третье решение, которое намного проще — нужно лишь внимательно посмотреть на формулу и подключить здравый смысл. Так и сделаем.
- У нас есть два выражения в скобках, произведение которых даёт 19.
- В первых скобках число точно больше 5, потому что там сумма пяти с чем-то другим.
Если мы разделим 19 просто на 5, то получим 3,8 — это самое большое, что может быть во вторых скобках, потому что чем больше значение в первых скобках, то тем меньше значение во вторых.
Самое большое значение, которое может быть в первых скобках — 8, когда m = 1. Это значит, что самое маленькое значение во вторых скобках — 19 / 8 = 2,375.
🤔 Получается, что значение вторых скобок лежит в диапазоне от 2,375 до 3,8.
Так как в скобках прибавляется 1/2, то отнимем её и от вторых скобок, и от диапазона. Получается так:
1,875 > n > 3,3
Единственные два целых числа, которые сюда подходят — это 2 и 3. Проверим их по очереди, подставив в исходное уравнение.
Если n = 2, то вторые скобки равны 2,5, и получается, что:
(5 + 3/m) × 2,5 = 19
5 + 3/m = 7,6
3/m = 2,6 → m = 1,15. Но так быть не может — по условию числа должны быть целыми.
Значит, остаётся только n = 3. Давайте проверим:
(5 + 3/m) × (3 + ½) = 19
(5 + 3/m) × 3,5 = 19, но 3,5 — это 7/2, поэтому (5 + 3/m) × (7/2) = 19
5 × 3/m = 19 / (7/2) = (19 × 2) / 7 = 38/7
3/m = 38/7 − 5 = 38/7 - 35/5 (потому что 5 = 35/7)
3/m = 3/7 → m = 7
Вот мы и нашли ответ без второго уравнения: m = 7, n = 3.
Короче: секрет был в том, чтобы обратить внимание на число 5 и условия задачи.
Программист и бизнес-план
К программисту пришёл друг и говорит:
— Слушай, у меня есть классный бизнес-план! Есть проект на 4 года, и на старте в него нужно вложить 10 миллионов. Я прикинул, что каждый год у нас будет прибыль 15% от всех вложенных средств, поэтому все проценты мы сразу вкладываем обратно в проект. Круто же?
— Круто, но денег не дам.
— Да я к тебе не за этим, деньги я нашёл. Ты лучше как программист мне помоги с такой штукой: я хочу каждый год в бизнес вкидывать сверху ещё денег, чтобы за 2 года мои 10 миллионов удвоились, а за 4 года — утроились. Сможешь мне написать программу, которая скажет, сколько миллионов надо вкладывать первые два года, а сколько — вторые два? Ну и округлить всё до миллионов, чтобы считать удобнее было.
Но программист не стал писать программу и строить финмодель, а посчитал всё за 5 минут на листочке. Это настолько впечатлило друга, что он взял товарища к себе главным разработчиком.
Но как вообще возможно посчитать такое за 5 минут?
Обозначим за X количество миллионов, которые нужно вкладывать в первый и второй год, а за Y — сколько миллионов нужно вкладывать в третий и четвёртый год.
Так как каждый год бизнес даёт прибыль 15%, то к началу второго года в нём будет 1,15 × 10 = 11,5 миллиона. Сразу после этого мы вкидываем в него X миллионов и получаем 11,5 + X.
Тогда к началу второго года мы получим снова 15% от денег в бизнесе:
1,15 × (11,5 + X) — и вкладываем сверху ещё X миллионов:
1,15 × (11,5 + X) + X — получается в бизнесе к началу третьего года
Но нам нужно, чтобы за первые два года бизнес удвоился, то есть к началу третьего года в нём было не 10 миллионов, а 20. Получаем такое неравенство:
1,15 × (11,5 + X) + X ⩾ 20
13,225 + 1,15X + X ⩾ 20
13,225 + 2,15X ⩾ 20 → 2,15X ⩾ 20 − 13,225 → 2,15X ⩾ 6,775
X ⩾ 3,15 — но так как у нас X должно быть целым, то ближайшее целое для этого неравенства X = 4.
Зная X, найдём сумму денег в бизнесе к началу третьего года:
13,225 + 8,6 = 21,825 миллиона
Сделаем то же самое для Y. К началу четвёртого года в бизнесе будет 1,15 × 21,825 + Y, а в самом конце четвёртого года мы снова получаем 15% прибыли:
1,15 × (1,15 × 21,825 + Y) + Y
1,3225 × 21,825 + 1,15Y + Y
28,8635625 + 2,15Y — будет в проекте через 4 года.
Но за 4 года первоначальные вложения должны утроиться, поэтому
28,8635625 + 2,15Y ⩾ 30
2,15Y ⩾ 1,1364375
Y ⩾ 0,52857 — но так как Y тоже должно быть целым, то ближайшее целое для этого неравенства будет Y = 1
Получается, что первые два года в бизнес нужно будет вкладывать по 4 миллиона, а вторые два — по одному.
Убойная задача из американского ЕГЭ про монеты
В США тоже есть ЕГЭ — причём он был задолго до нас. Вот одна задачка оттуда. Мы перевели её на русский и заменили центы на привычные рубли. Сама задача звучит так:
- Существуют Елена, Иван.
- Существуют монеты двух номиналов: рублёвые и пятирублёвые.
- У Елены и Ивана одинаковое число монет.
- У Елены 64 рублёвых монетки и сколько-то пятирублёвых монет. Все её монеты вместе весят 1,134 килограмма.
- У Ивана 104 рублёвые монетки и сколько-то пятирублёвых монет.
- Каждая пятирублёвая монета на 2,7 грамма тяжелей рублёвой.
Вопросы:
- У кого больше денег и на сколько больше?
- Сколько весят монеты Ивана?
Эту задачку можно решить на листочке за несколько минут. Попробуйте сами, а если не получится — кат в помощь ↓
Находим, у кого больше денег
Это звучит удивительно, но для решения нам не нужно считать точное количество монет обоих видов у каждого (хотя никто не мешает вам попробовать это сделать). Вместо этого мы применим хитрость и смекалку.
Нам неважно, сколько у кого монет, главное, что их одинаковое количество и у Елены, и у Ивана, а вот количество рублёвых монет разное. Зная это, достаточно нарисовать простую картинку, по которой легко найти ответ на этот вопрос:
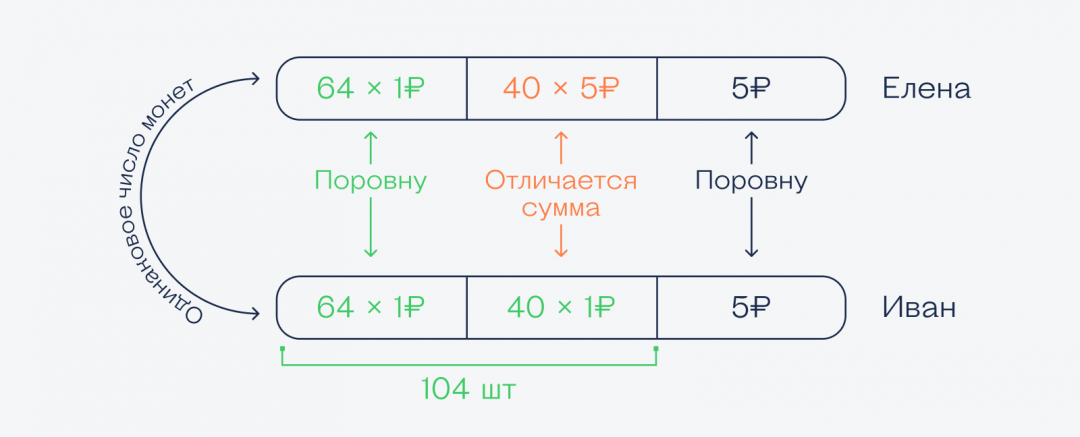
Глядя на неё, понимаем, что общую часть из 64 рублёвых монет можно выкинуть у обоих, потому что и там и там одинаковая сумма. А то, что осталось, и даст нужную разницу.
👉 Так как количество монет у каждого одинаковое, то у Ивана вместо 40 пятирублёвок лежит 40 рублёвых монет, а остальные пятирублёвки снова у обоих в одинаковом количестве, и их тоже можно отбросить. Получается, разница в деньгах такая:
- у Елены — 40 × 5 ₽ = 200 ₽;
- у Ивана — 40 × 1 ₽ = 40 ₽.
Значит, у Елены на 200 − 40 = 160 ₽ больше.
Находим вес монет Ивана
На этом этапе спотыкается большинство решающих, потому что они пытаются найти точное количество монет Ивана. Но мы-то с вами уже знаем, что это необязательно — достаточно найти разницу в весе и по ней посчитать вес монет.
Используем тот же рисунок, но уже в разрезе веса монет:
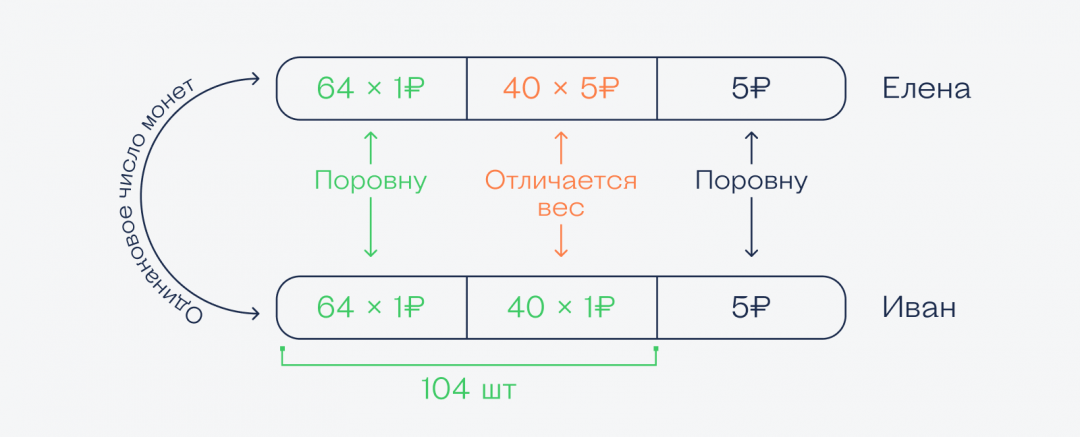
Получается, что разница в весе зависит от тех же монет, что мы считали в первой части.
Так как одна рублёвая монета легче одной пятирублёвой на 2,7 грамма, то у 40 монет разница в весе будет 40 × 2,7 = 108 грамм. А раз у Ивана пятирублёвок меньше, чем у Елены, то и монеты будут весить как раз на эти 108 грамм легче: 1,134 − 0,108 = 1,026 килограмма.
Задача про тест на собеседовании
Один джуниор пришёл на собеседование в крупную ИТ-компанию, и ему дали тест из 50 вопросов. За каждый правильный ответ он получал 9 баллов, а за каждый неправильный отнимали 17 баллов. Если же просто пропустить вопрос, то за него ничего не давали и не списывали.
Чтобы устроиться на работу, нужно или набрать 170 баллов в тесте, или дать больше 30 правильных ответов. Джуниор набрал 153 балла, при этом он точно знал, что как минимум в одном вопросе он ошибся.
Взяли ли его на работу?
Мы не знаем, как отвечал джуниор, поэтому обозначим всё так:
x — количество правильных ответов;
y — количество неправильных ответов;
z — сколько вопросов осталось без ответа.
При этом мы помним, что джуниор точно ошибся как минимум в одном вопросе, поэтому игрек у нас будет больше либо равен единице.
Зная, что всего вопросов было 50, можем составить уравнение: x + y + z = 50.
Так как за каждый правильный ответ джуниор получал 9 баллов, а за неправильный снималось 17, составим второе уравнение: 9x − 17y + 0z = 153.
Получаем систему из двух уравнений:
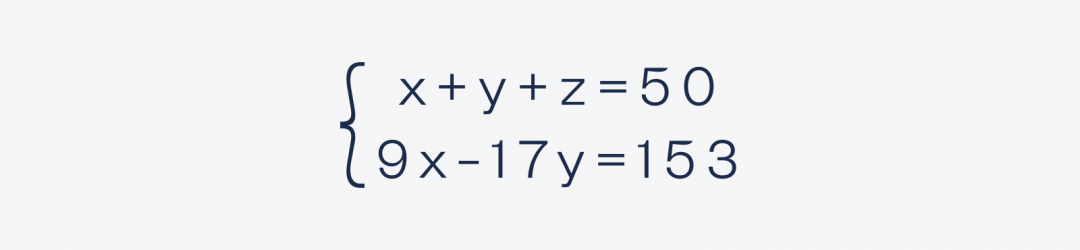
Второе уравнение выглядит проще, поэтому займёмся им.
9x − 17y = 153
9x − 153 = 17y ← вынесем здесь 9 за скобки, как множитель в левой стороне
9(x − 17) = 17y
В последнем уравнении видно, что левая часть делится на 9 без остатка (потому что там есть множитель 9). Это значит, что 17y тоже должно делиться на 9 без остатка, а раз 17 на 9 не делится, то делится игрек. Получается, что он может быть равен 9, 18, 27, 36 или 45 (больше быть не может, потому что общее число вопросов у нас 50).
Проверим все эти числа по очереди.
✅ Если y = 9, то (x − 17) = 17 (мы используем последний вид второго уравнения), а значит, x = 34. Если x = 34, то z = 50 − 34 − 9 = 7. Вроде сходится, но надо проверить остальное.
❌ Если y = 18 = 9 × 2, то (x − 17) = 17 × 2, а значит, x = 51. Но число вопросов у нас 50, поэтому y = 18 не подходит.
❌ Если y = 27 = 9 × 3, то (x − 17) = 17 × 3, а значит, x = 68. Но число вопросов у нас 50, поэтому y = 27 не подходит.
❌ Видно, что с ростом игрека у нас начинает сильно расти x, который давно выбился за допустимые 50 вопросов, поэтому остальные варианты (36 и 45) тоже не подходят.
А раз так, то остаётся только один, самый первый вариант, где x = 34. Этого достаточно, чтобы джуниора взяли на работу.
Сложная задача про длину кабеля
Воскресенье, утро, Стамбул. Сетевой инженер из России пьёт кофе в кафе с видом на Босфор. Вдруг звонок:
— Васян, выручай, нужно срочно продиагностировать кусок сети, без тебя никак.
— В чём дело?
— У нас два компьютера соединены через два шлюза. Нам нужно понять скорость сигнала между этими шлюзами.
— В смысле? Ну зайдите на шлюз и сделайте пинг. Он вам скажет точное время прохождения сигнала.
— Мы не можем, у нас нет пароля, а у кого он — никто не знает.
— Ладно, что вы ещё знаете?
Дальше он узнал вот что:
- Есть два компьютера.
- Между ними два шлюза: красный и синий.
- Между двумя шлюзами ещё какие-то устройства: серверы, передатчики, шлюзы и т. д. — мы не знаем какие. Они замедляют сигнал.
- Мы не знаем точный пинг (то есть время прохождения сигнала) между всеми этими точками.
- Но если прогнать пинг от первого компьютера до красного шлюза и сравнить с пингом от красного шлюза до второго компьютера, то разница в пинге будет 35 миллисекунд.
- А если сравнить пинг до и от синего шлюза, то разница будет уже 25 миллисекунд.
- Скорость пинга одинаковая в обе стороны всё время.
Задача — узнать пинг (то есть скорость прохождения сигнала) между красным и синим шлюзом. Предположительно там стоит какое-то оборудование, которое замедляет наш сигнал слишком сильно, и в зависимости от показателей замедлений нужно дать кому-то по шапке.

Василий поспорил, что сможет решить эту задачу, даже не открывая компьютера. В выпадайке — как ему это удалось.
Нарисуем схематично наше соединение с двумя шлюзами, красным и синим. Условно будем считать, что длина каждого отрезка соответствует скорости обработки сигнала:

Теперь обозначим за x, y и z три отрезка сигнала, которые нам неизвестны, и подпишем разницу в пинге — это то, что мы знаем:
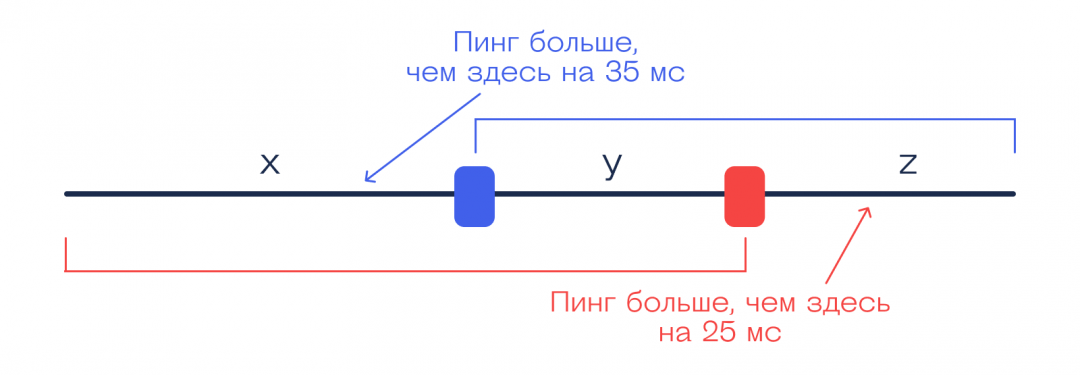
По рисунку можно составить два уравнения:
x + y − z = 25 ← когда пингуем красный шлюз
y + z − x = 35 ← когда пингуем синий шлюз
Сложим эти уравнения друг с другом:
x + y − z + y + z − x = 25 + 35
Сгруппируем неизвестные друг с другом:
(x − x) + (y + y) + (z − z) = 60
2y = 60 → y = 30
Получается, пинг между шлюзами, которое мы обозначили за y, равен 30 миллисекунд.
Задача про скорость тестирования
Несложная математическая задача, чтобы размять мозги.
Один тестировщик заметил, что его коллега всё время уходит с работы на 2 часа раньше него. Как-то перед очередным таким уходом он спросил:
— Слушай, а почему ты всё время уходишь раньше меня?
— Потому что я ухожу сразу, как делаю норму в 80 тестов в день, а ты хочешь премию, поэтому делаешь 90 тестов.
— Да, всё так. Но если я захочу уходить раньше на пару часов, как ты, и при этом делать норму в 80 тестов, что мне нужно для этого?
— Просто делай на один тест в час больше, чем сейчас, — ответил продуктивный коллега и ушёл домой.
👉 Сколько тестов в час нужно делать второму тестировщику, чтобы тоже уходить домой пораньше, как первый?
Мы не знаем, сколько часов в день работает первый тестировщик, поэтому обозначим это время за X. Тогда второй тестировщик, который уходит на 2 часа позже, работает X+2 часов в день.
Получается, что первый делает 80 / X тестов в час, а второй — 90 / (X + 2) тестов в час.
Мы знаем, что если он будет делать на 1 тест в час больше, то сравняется по скорости с первым тестировщиком. Запишем это в виде равенства:
80 / X = (90 / (X + 2)) + 1
В правой части у нас есть дробь с делителем (X + 2). Чтобы прибавить единицу к этой дроби, применим математический трюк — сделаем её тоже в виде дроби с таким же знаменателем:
1 = (X + 2) / (X + 2)
Возникает вопрос, насколько правомерна эта замена — например, есть ли условия, при которых в знаменателе будет ноль? Смотрим: у нас рабочие часы всегда будут положительным числом. Чтобы в знаменателе был ноль, X должен быть равен минус двум, а такого рабочего времени быть не может. Значит, мы ничего не ломаем, такая подстановка возможна:
80 / X = (90 / (X + 2)) + 1
↓
80 / X = (90 / (X + 2)) + (X + 2) / (X + 2)
Для наглядности нарисуем это в более традиционном формульном виде:
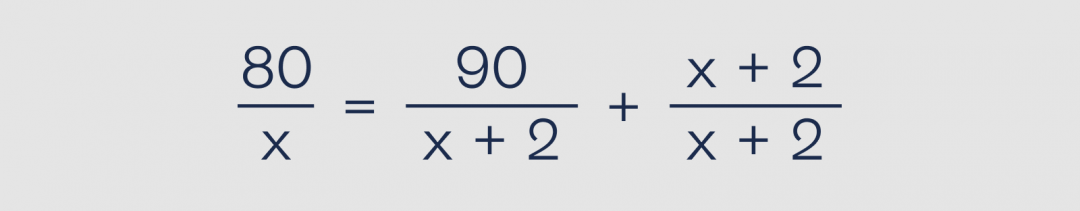
Складываем дроби справа:
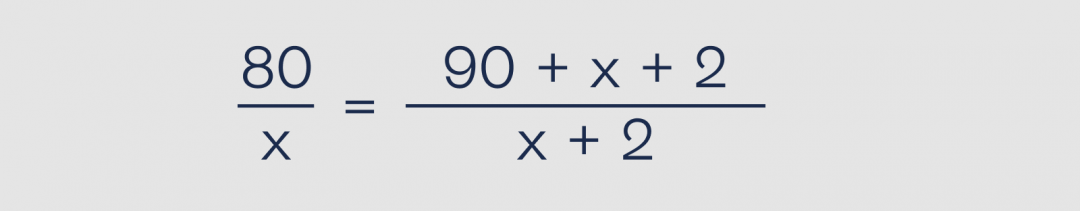
Чтобы избавиться от дроби, нам нужно перемножить левую и правую часть на произведение делителей, то есть на X × (X + 2):
80 × (X + 2) = (92 + X) × X
Ну а дальше изи:
80X + 160 = 92X + X²
Переносим всё в правую часть и получаем квадратное уравнение:
X² +92X – 80X – 160 = 0
X² + 12X – 160 = 0
Решаем его через любой онлайн-калькулятор квадратных уравнений и получаем два ответа: X = 8 и X = –20. Так как у нас количество рабочих часов не может быть отрицательным, то остаётся только один ответ — 8 часов работает первый тестировщик и делает 80 / 8 = 10 тестов в час.
Получается, что второму тестировщику тоже нужно делать 10 тестов в час.
Простая и сложная задачи с собеседования
Две задачи с собеседований на позиции в бигдате, машинном обучении и нейросетях. Для работы там нужно знать математику и находить хитрые пути решения. Обе задачи как раз из таких.
Очень простая задача. Найти, чему равен X в этом уравнении:
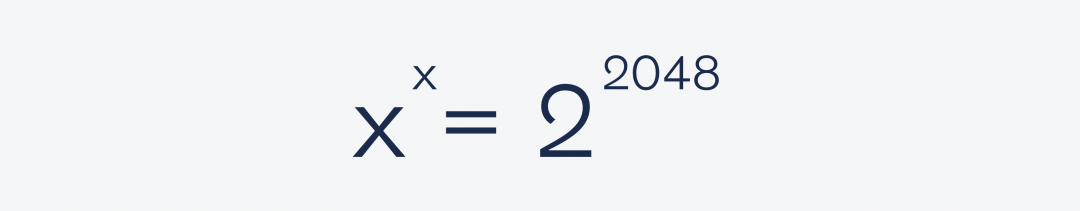
Несмотря на мнимую сложность и степени, эта задача решается за минуту. Всё, что нам понадобится, — это известное ещё со школы свойство перемножения степеней, которое работает так:
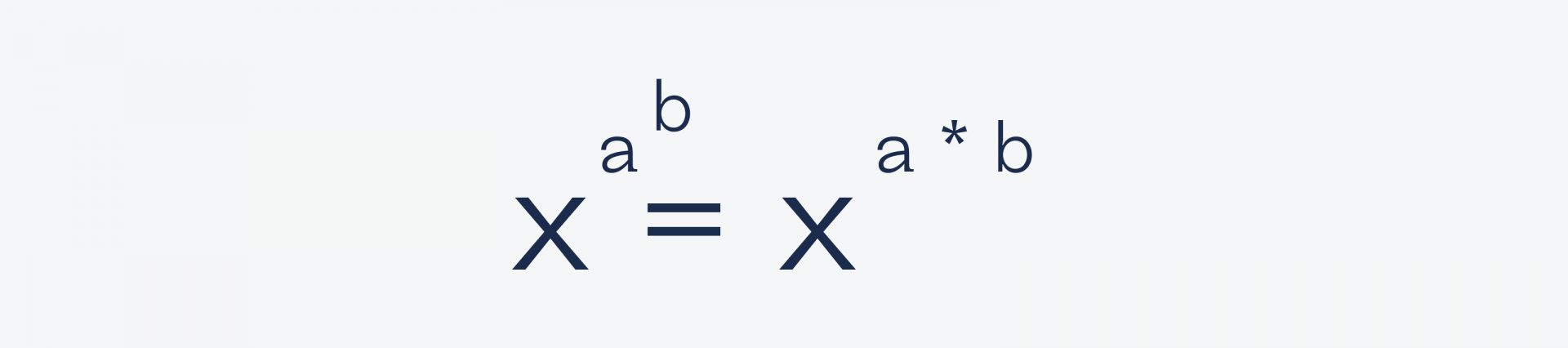
Теперь используем это, чтобы сравнять основание и степень в левой части:
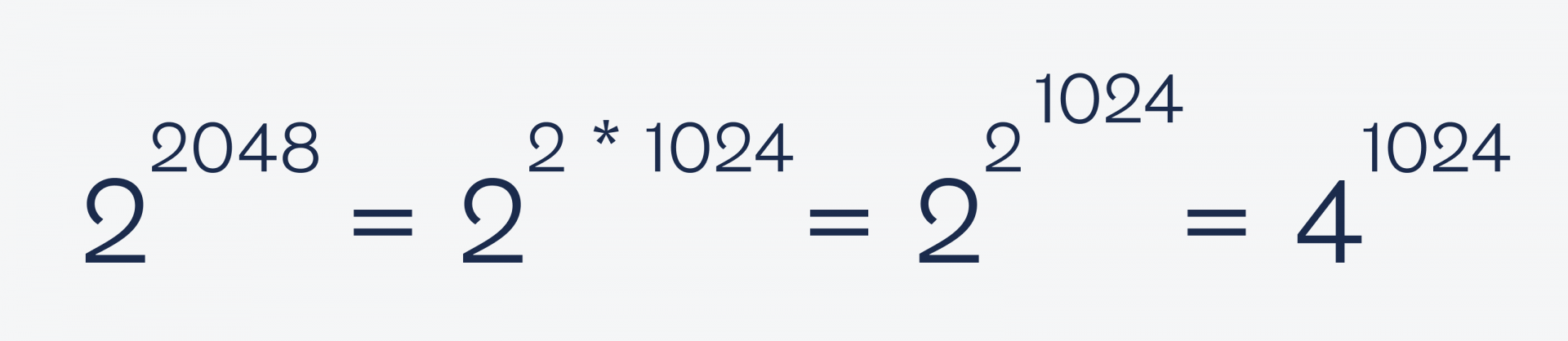
Дальше так же выносим двойку из каждой степени и возводим в неё основание, пока числа не станут равны:
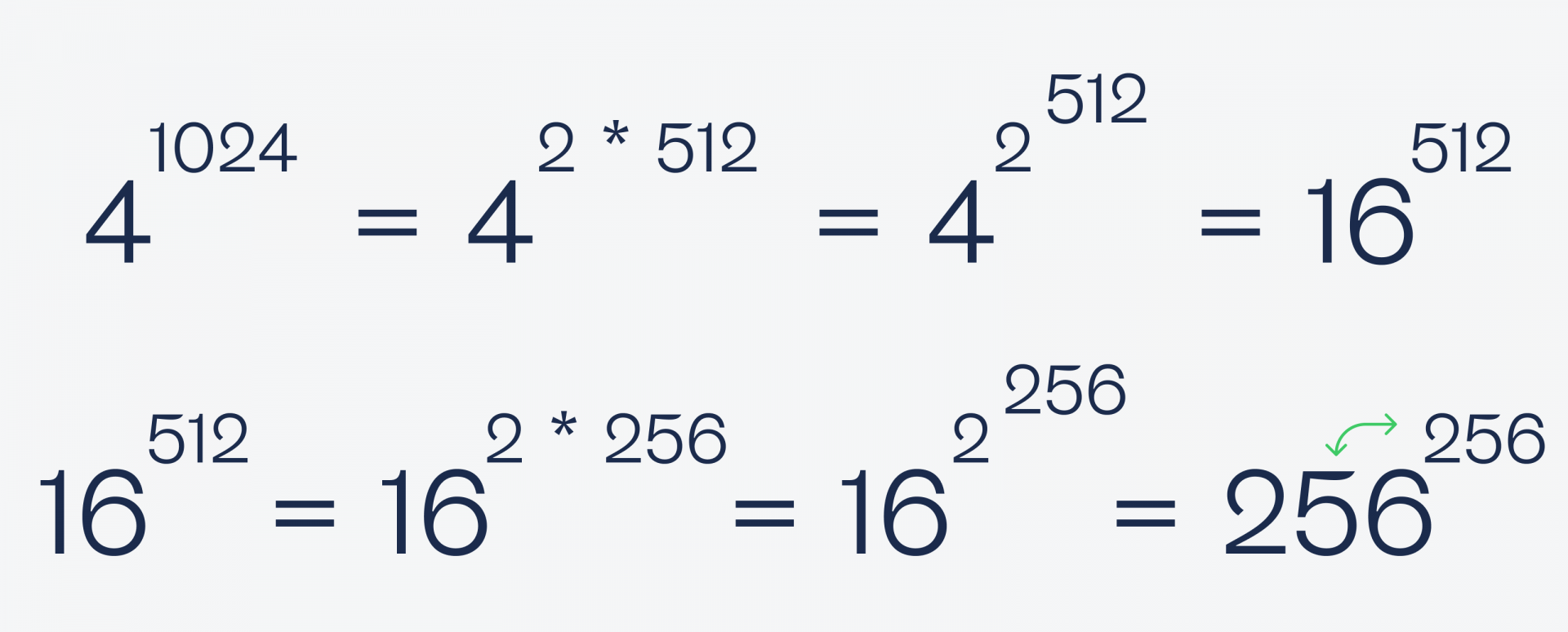
Очень сложная задача. Без калькулятора найти, чему это равно:
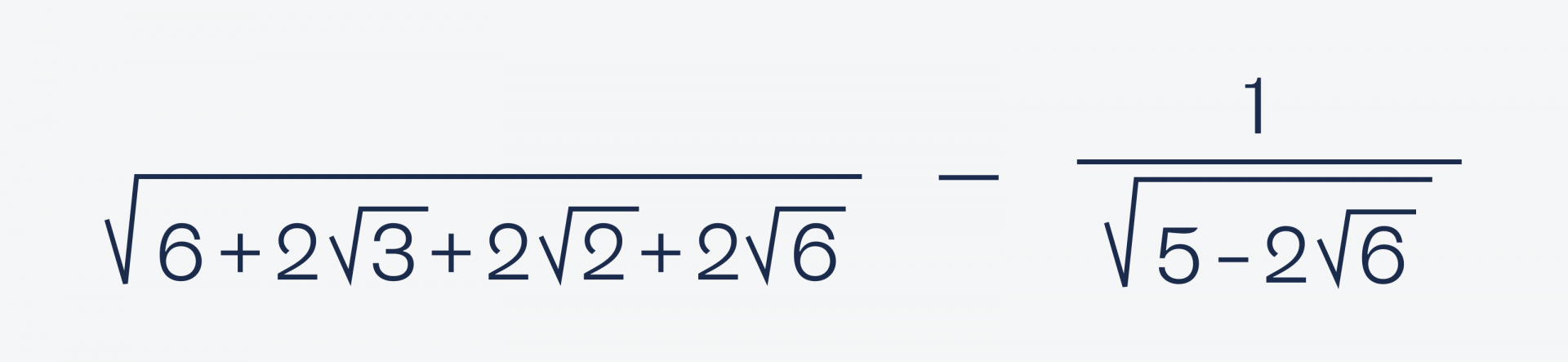
Это одна из тех задач, где в итоге всё получается просто и красиво. Сейчас убедимся в этом.
Сначала поработаем с левой частью: в ней есть √6. Чтобы его получить, нужно √2 умножить на √3.
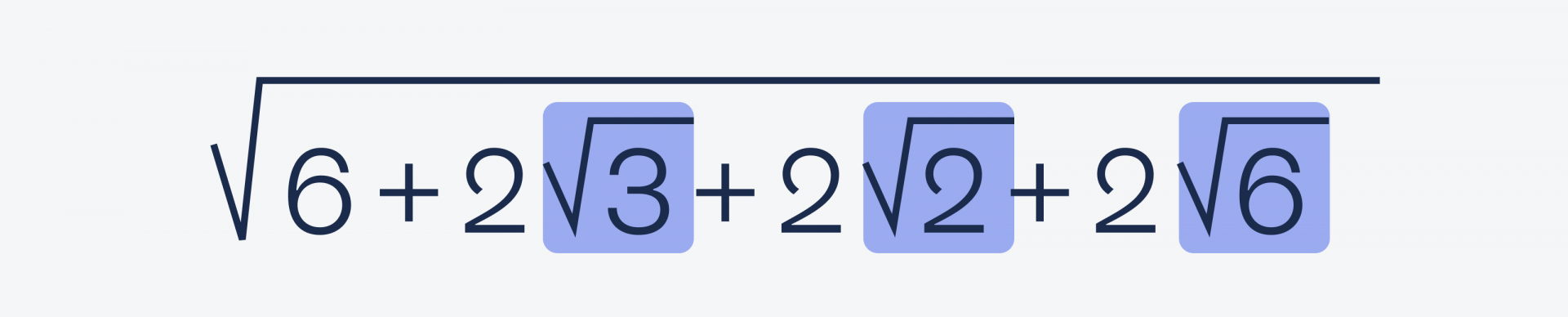
Но 2√6 — это удвоенное произведение, которое встречается в формуле квадрата суммы: (a + b)² = a² + 2ab + b².
Попробуем подставить сюда вместо a — √3 и вместо b — √2, чтобы получить удвоенное произведение, и посмотрим, что получится:
(√3 + √2)² = (√3)² + 2√2√3 + (√2)² = 3 + 2√6 + 2 = 5 + 2√6
Мы только что выяснили, что (√3 + √2)² = 5 + 2√6 — запомним это на будущее. А теперь посмотрим на левую часть под корнем ещё раз: в ней есть не 5 + 2√6, а 6 + √6, то есть на единицу больше:
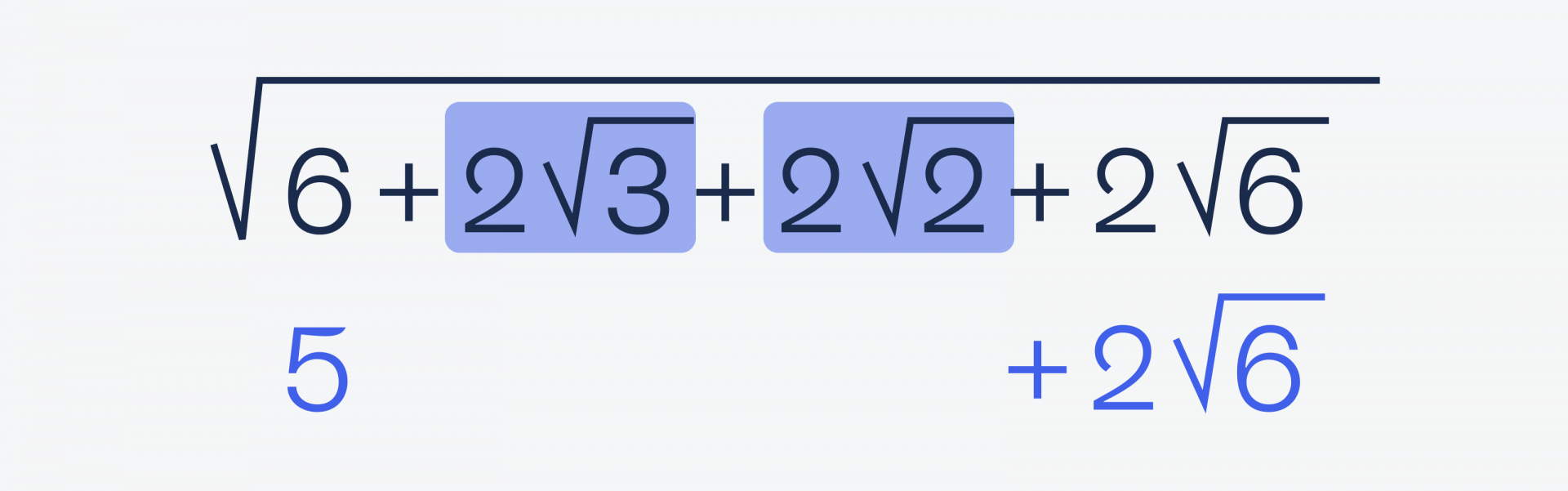
И там же есть удвоенные числа √2 и √3 — это значит, что мы можем проверить снова, вдруг из этого тоже можно сделать квадрат суммы.
Теперь самая сложная часть решения: раз 6 − 5 = 1, то пусть первым слагаемым будет единица, а вторым — (√3 + √2), чтобы мы получили 5 + 2√6 после возведения второго в квадрат. Проверим эту теорию:
(1 + (√3 + √2))² = 1² + 2(√3 + √2) + (√3 + √2)² = 1 + 2√3 + 2√2 + (√3 + √2)²
Но мы помним, что (√3 + √2)² = 5 + 2√6, поэтому вот что у нас получается:
1 + 2√3 + 2√2 + 5 + 2√6 = 6 + 2√3 + 2√2 + 2√6
Это именно то, что стоит у нас под корнем, значит, в левой части мы извлекаем корень из квадрата — а это будет равно как раз тому, что стоит в скобках:
√(1 + (√3 + √2))² = 1 + √3 + √2
Мы расправились с левой частью, теперь перейдём к правой:
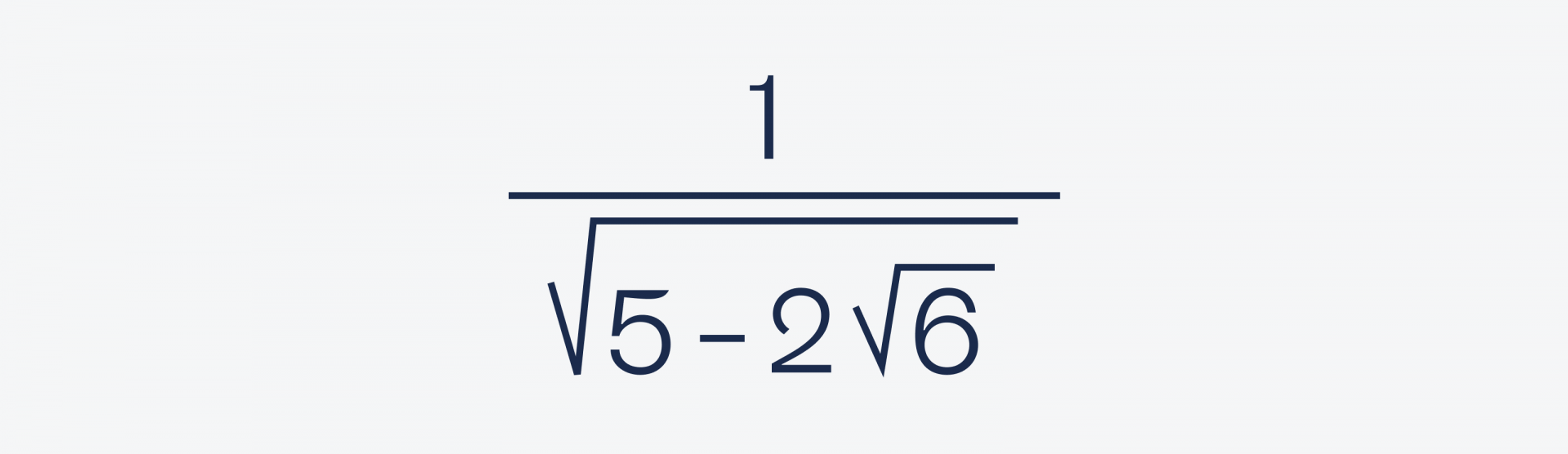
Чтобы избавиться от корня в знаменателе, умножим обе части на одно и то же число — √(5 + 2√6). Благодаря этому мы сможем возвести в квадрат оба слагаемых, потому что есть такое правило: (a + b) × (a − b) = a² − b².
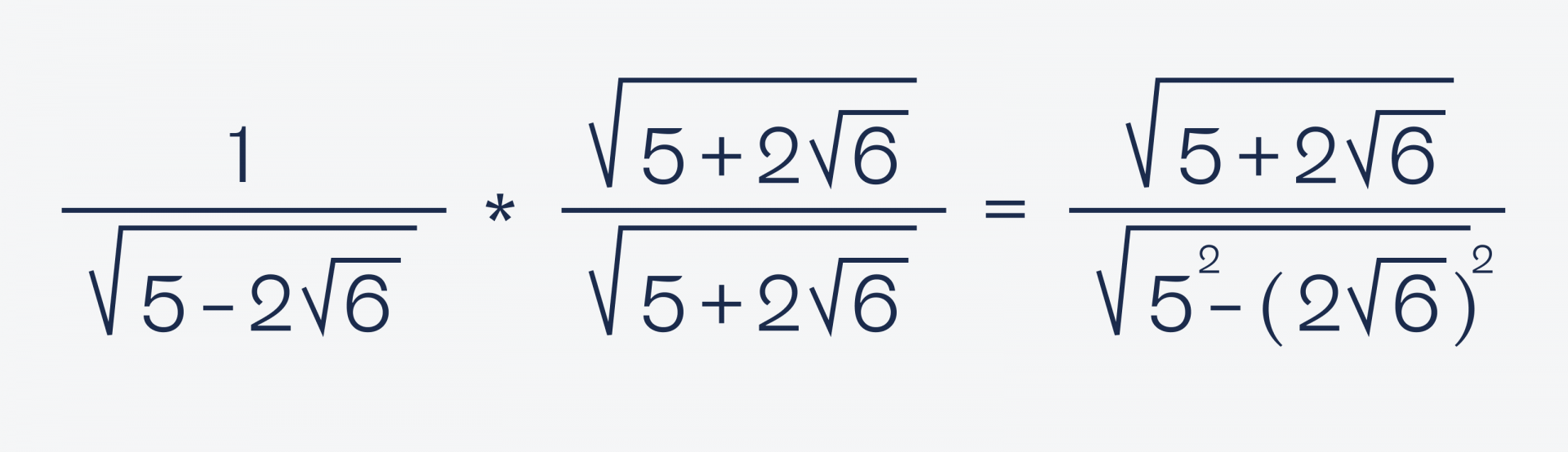
Посчитаем знаменатель:

Выходит, что вся наша дробь равна √(5 + 2√6). Но мы помним из первой части, что:
√(5 + 2√6) = (√3 + √2)²
Подставим это под знак корня:
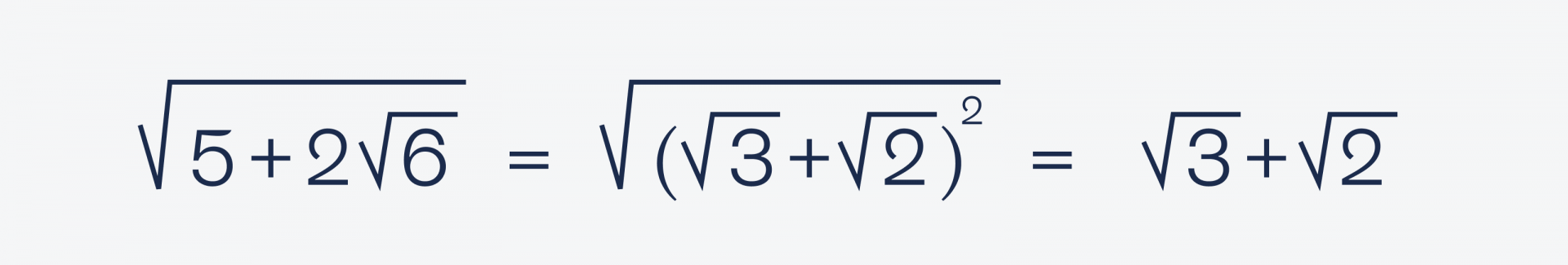
Значит, наша правая часть равна √3 + √2. Теперь отнимем это от левой части:
1 + √3 + √2 − (√3 + √2) = 1 + √3 − √3 + √2 − √2 = 1
Получилась единица — простая и красивая, как мы и ожидали.
Школьная задача, которую дети решают без калькулятора, а взрослые — нет
Такую задачу дают в седьмом классе на проверку усвоения материала, а ещё — на собеседованиях в ИТ-компании, чтобы проверить находчивость соискателей. Её обычно или решают за пару минут без калькулятора, или тратят на это полчаса, или пишут код, который всё посчитает сам.
Теперь задача — найти значение суммы и разности квадратов от 1 до 100:
1² − 2² + 3³ − 4² + 5² − 6² + … + 99² − 100² = ?
Очевидно, что можно посчитать значение каждого квадрата, а потом вычитать и складывать все значения по очереди. Но это долго и так собеседование мы точно не пройдём.
Используем математическую хитрость и посмотрим на пример с точки зрения разности квадратов. Для начала расставим скобки:
(1² − 2²) + (3³ − 4²) + (5² − 6²) + … + (99² − 100²)
Мы никак не изменили значение выражения, но у нас появилась сгруппированная разность квадратов. Вспомним формулу разности квадратов:
x² − y² = (x − y)(x + y)
Применим её к каждому выражению в скобках:
(1 − 2)(1 + 2) + (3 − 4)(3 + 4) + … + (99 − 100)(99 + 100)
В каждой скобке, где есть минус, значение разности равно −1, потому что числа идут по порядку и в каждой паре второе число больше первого на единицу. Получается, что первая скобка в каждом произведении равна −1:
−1(1 + 2) +(−1)(3 + 4) + … + (−1)(99 + 100)
Вынесем общий минус за скобки:
−1 (1 + 2 + 3 + 4 + … + 99 + 100)
Получается, нам нужно найти сумму от 1 до 100 и умножить её на −1. Для этого вспомним такую формулу:
сумма чисел от 1 до N равна произведению N на N+1, поделённого пополам.
В нашем случае сумма от 1 до 100 считается так:
(100 × 101) / 2 = 10100 / 2 = 5050
Умножаем это значение на −1 и получаем общий ответ: −5050
Хитрые программисты могут потратить эту пару минут не на математику, а на организацию простого цикла:
// тут будет результат
var res = 0;
// с помощью этой переменной мы будем чередовать плюс и минус в выражении
var index = 1;
// перебираем числа от 1 до 100 включительно
for (let i = 1; i <= 100; i++) {
// возводим число в квадрат, ставим нужный знак из индекса и добавляем всё к результату
res = res + index * i * i;
// меняем знак для следующего действия
// если индекс был положительный, то после умножения он становится отрицательный — так мы меняем плюс на минус и наоборот
index = index * (-1);
}
// выводим результат
console.log(res)Запустите код в консоли браузера, чтобы посмотреть результат. А если вы успели напечатать это за 2 минуты и понять, что означает каждая строчка, — приходите в Практикум прокачивать свои знания и получать новую профессию.