Долгие выходные подошли к концу, впереди трудовая неделя, а вы чувствуете, что не готовы? Потренируйтесь на этих задачках, они помогут вернуть мозг в рабочее состояние.
Хитрый электрик и немаркированные провода
Компания друзей собралась перед окончанием праздников. Делились историями с работы, и кто-то рассказал, как его организация проводила интернет на остров — от левого берега реки до правого.
Под водой проложили 49 проводов, но они оказались одного цвета, а подрядчик забыл их промаркировать. Позвали электрика, чтобы он пронумеровал все провода на левом и правом берегах так, чтобы числа совпадали. Ему дали катер, чтобы пересечь реку сколько угодно раз, линию с током на левом берегу и мультиметр, который показывает напряжение в проводе. И электрик справился.
— Ну, он, наверное, пересёк реку минимум 49 раз.
— Нет, ему хватило двух — туда и обратно. А потом он просто долго сидел на правом берегу и смотрел на воду.
— Но как?
На исходном берегу электрик подал напряжение на случайный провод и пометил его как №1. Все остальные 48 проводов он попарно соединил между собой так, чтобы на левой стороне получился один провод под напряжением и 24 пары. После этого электрик отправился на правый берег (первая поездка).
Приплыв на место, он с помощью мультиметра нашёл провод под напряжением — это провод № 1, и он его так и пометил. А дальше начинается электрическая магия.
Электрик взял провод № 1 под напряжением, соединил его с любым другим проводом и подписал его как № 2. Мы помним, что на левом берегу провода соединены попарно, значит, провод № 2 с той стороны с чем-то соединён, а, значит, ток вернулся обратно и появился в новом проводе, который электрик подписал как № 3.
Дальше всё то же самое: электрик взял провод с током № 3, соединил его с любым оставшимся проводом и подписал новый провод как № 4. Электрик помнил про пары на том берегу, поэтому нашёл провод, в котором снова появился ток, и подписал его как № 5. Таким же образом он соединил оставшиеся провода и нумеровал все жилы на правой стороне от 1 до 49. Сделав это, электрик вернулся на левый берег (вторая поездка).
Осталось самое интересное — как на этом берегу проставить те же самые числа на проводах. Электрик знал, как выглядит провод № 1, потому что он его подписал, но не знал, как выглядит провод № 2.
Но он помнил, что провод № 1 соединён на том берегу с проводом № 2, который на этом берегу соединён с проводом № 3. Значит, задача электрика в том, чтобы найти это соединение на левом берегу. Для этого он разъединял по очереди все соединения и смотрел, пропал ли ток во всех остальных проводах. Если не пропал во всех остальных — значит, разъединил не ту пару и её надо вернуть на место. А если пропал — значит, электрик нашёл соединение проводов № 2 и № 3. При этом неизвестный провод, который остался под напряжением, будет провод № 2, а тот, с которым он соединялся, будет № 3.
После этого электрик соединил подписанную пару обратно и начал искать следующую точку, которая отключает все остальные жилы, — это будут провода № 4 и № 5. Действуя по этой схеме, хитрый электрик подписал все оставшиеся провода. Провайдеру осталось только разъединить пары на каждом берегу.
Айтишники, учёные и поездка на остров
Все оценили находчивость электрика, и кто-то спросил, были ли ещё забавные истории с тем островом.
— Были. Нужно было переправить на остров шесть сотрудников: трёх айтишников и трёх учёных. В катере помещалось всего двое, причём айтишники умели им управлять, а учёные — нет. И было важно не оставлять на одном берегу больше учёных, чем айтишников, иначе они взорвали бы мозг айтишникам разговорами о предстоящих проектах, а тем нужно думать над своей работой.
— И как, переправили без происшествий?
— Конечно! А потом купили катер побольше, чтобы больше так не заморачиваться.
— А как переправили?
Для первой поездки есть четыре варианта:
- один айтишник — не подходит, потому что на берегу учёных становится больше и они взорвут мозг;
- два айтишника — не подходит по той же причине;
- один или два учёных — тоже нет, потому что они не умеют управлять катером;
- айтишник и учёный — единственный вариант, который остаётся.
Значит, первым рейсом пара на остров отправляется пара «учёный-айтишник». Теперь катер надо как-то отправить назад. Но так как учёный не умеет им управлять, он остаётся на берегу, а айтишник — возвращается. Учёных на исходном берегу получается меньше, они не взрывают никому мозг.
Теперь прикинем варианты следующего рейса. Мы не можем отправить двух айтишников, иначе учёные останутся в большинстве, и конфликта на левом берегу не миновать.
Поэтому снова на тот берег уплывают учёный с айтишником. Причём айтишник высаживает учёного, но сам из катера не вылезает — если так не сделать, то он окажется с двумя учёными на острове и они увлекут его разговорами о своих исследованиях.
Айтишник возвращается. Таким образом, у нас на острове два учёных, а на левом берегу — один учёный и три айтишника, которые могут спокойно думать о своей работе.
Теперь нужно сделать выбор, кто поедет на этот раз. Можно отправить снова учёного и айтишника, но тогда на левом берегу окажутся три учёных. И безопасно перевезти остальных айтишников поодиночке уже не получится — учёные всегда будут в большинстве. Значит, остаётся только один вариант: отправить в путь двух айтишников. В итоге на том берегу всех поровну и всё проходит спокойно.
Но катер надо как-то отправить обратно с острова. Нельзя разместить на ней одного айтишника, потому что второй останется в меньшинстве среди учёных. Двум айтишникам ехать обратно тоже не вариант, потому что они только что прибыли. Поэтому назад отправляются учёный и айтишник. Теперь единственный безопасный вариант — отправить на остров двух айтишников.
Назад отправим одного айтишника. Чтобы не выходить из катера, он позовёт в него учёного (например, вопросом «Над какой вакциной вы сейчас работаете?») и вернётся с ним обратно на остров.
Точно так же забираем оставшегося на левом берегу учёного. И в итоге вся компания оказывается на острове, и никто никому не взорвал мозг.
Находчивый айтишник и тысяча пробирок
— Ох уж эти учёные…
— И не говори! Была у нас ещё история…
Учёным прислали тысячу пробирок с лекарством, которое нужно было опробовать на людях, и почти сразу оказалось, что в одной из пробирок ядовитый реактив. Внешне его было никак не отличить от лекарства, поэтому вся партия оказалась опасной для людей.
У учёных были лабораторные мыши, но из них можно было использовать только 10, остальные были нужны для других исследований. Но пробирок тысяча, а времени мало. Тогда учёные обратились к программистам за советом, и те придумали способ, как найти пробирку с ядовитым реактивом всего за день.
— А что за способ?
Чтобы найти пробирку с ядом за один день, нам надо призвать на помощь двоичную систему счисления. Но для начала разберёмся с привычной — десятичной.
Десятичная система счисления
Она самая знакомая из всех, и мы ей пользуемся каждый день. В её основе — 10 цифр, от 0 до 9, поэтому она и называется десятичной.
Мы пользуемся десятичной системой, особо не рефлексируя. Например, мы видим число 436 — мы автоматически его раскладываем: четыре сотни + три десятка + шесть.
Только что мы разложили число на разряды: 4 — это разряд сотен, 3 — разряд десятков, 6 — разряд единиц. Получается, что:
436 = (4 × 100) + (3 × 10) + (6 × 1)
436 = (4 × 10²) + (3 × 10¹) + (6 × 10 в нулевой степени)
Получается, что наша десятичная запись числа — это просто краткая форма записи длинного выражения, где какие-то числа умножаются на десятки в разных степенях.
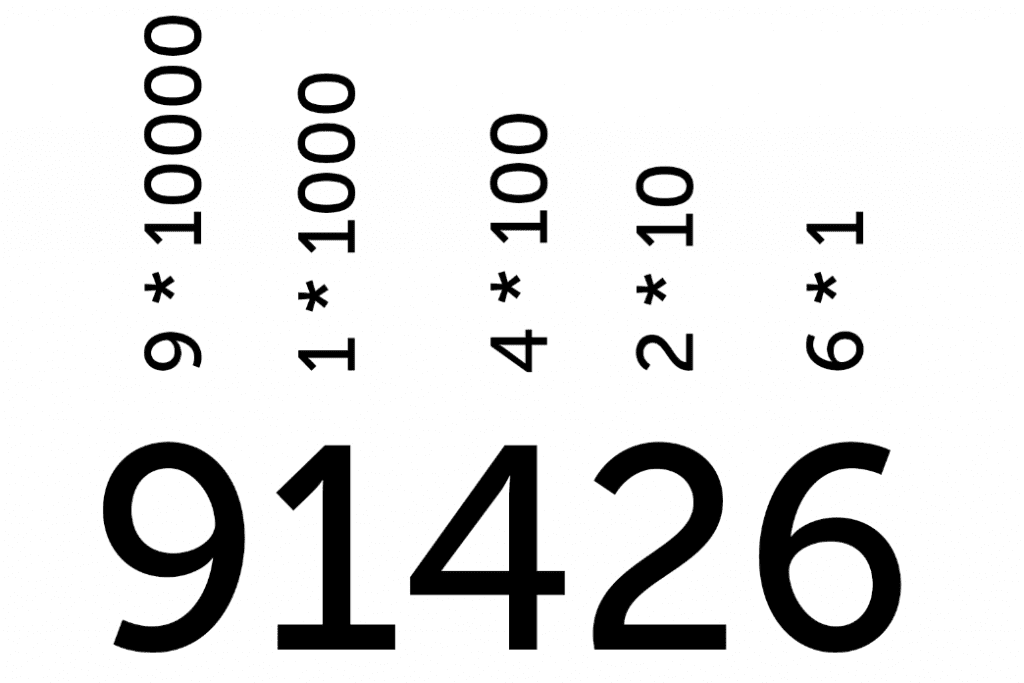
Двоичная система
Двоичная система — это то же самое, только вместо десятки — двойка. Вместо степеней десятки мы используем степени двойки. Вместо десяти цифр от 0 до 9 мы используем две: 0 и 1.
Чтобы перевести числа из двоичной системы счисления в десятичную, нужно то же самое, что и раньше: возводить двойку в степень разряда и умножать на 0 или 1. Рассмотрим на примере:
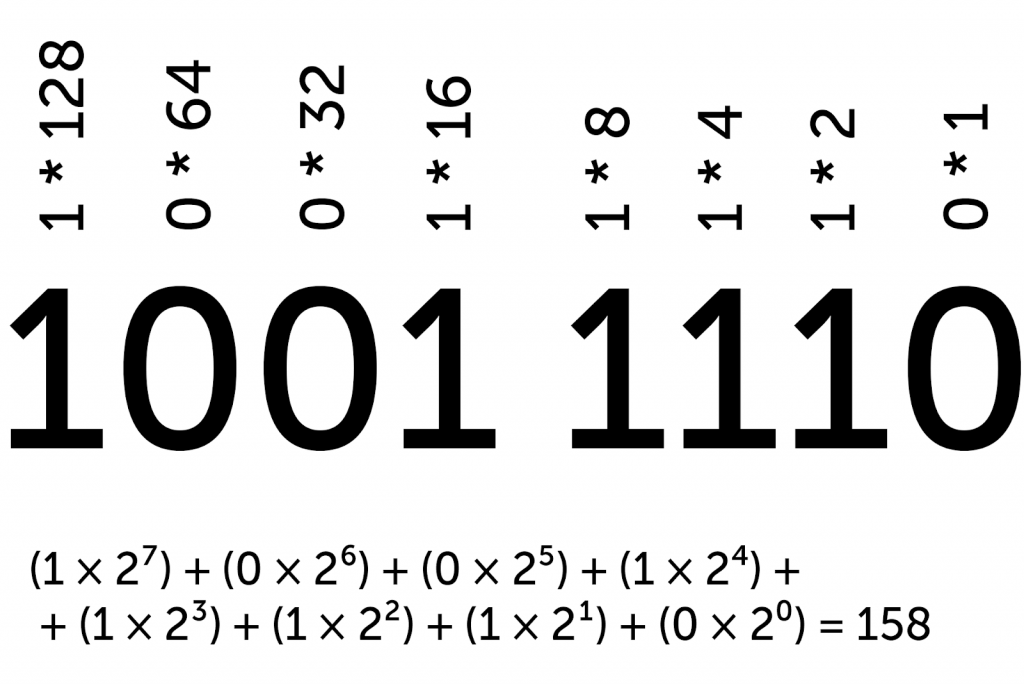
Любое десятичное число можно представить в виде двоичного, и наоборот. Теперь попробуем использовать это знание в решении задачи.
Битовая глубина
У нас 1000 пробирок. Запишем это число в двоичной системе счисления:
1000 в десятичной = 1111101000 в двоичной
Это максимальное число, которое нам понадобится при нумерации, и оно состоит из 10 нолей и единиц. Получается, что битовая глубина решения этой задачи — 10. А у нас как раз 10 мышей. Это и будем использовать при расчётах.
Немного магии
Зная, что у нас 10 бит на число, пронумеруем каждую пробирку таким образом:
1 — 0000000001
2 — 0000000010
3 — 0000000011
4 — 0000000100
…
999 — 1111100111
1000 — 1111101000
Затем расставляем мышей в клетки по порядку, чтобы они никуда не бегали и всегда оставались на своих местах. Пусть клетки стоят слева направо.
А теперь начинается магия. Берём каждую пробирку и смотрим, на каких местах стоят единицы. Мышам в этих клетках даём каплю вещества:
первая пробирка: 0000000001 — даём каплю мыши в самой правой клетке
вторая пробирка: 0000000010 — даём каплю мыши во второй клетке справа
третья пробирка: 0000000011 — даём по капле двум мышам из первой и второй клеток справа
четвёртая пробирка: 0000000100 — даём каплю мыши в третьей клетке справа
…
999 пробирка: 1111100111 — даём по капле мышам из первых пяти клеток слева, пропускаем две клетки, дальше капаем трём оставшимся
Таким образом, каждая пробирка получила свою уникальную комбинацию из мышей. И на следующий день, когда часть мышей умрёт, мы сразу узнаем номер пробирки с ядом: оставшихся в живых мышей запишем как 0, а погибших — как 1.
Например, наутро мы заметили, что шесть мышей слева и одна справа живы, остальные три мертвы. Запишем это в двоичной системе:
0000001110
Переведём вручную или на калькуляторе это в десятичную систему и получим число 14. Это и есть номер нашей пробирки с ядом.
В чём секрет
Секрет в том, что комбинация нолей и единиц уникальна для каждой пробирки. И раз мы даём по капле тем мышам, которые соответствуют единице, то, если в них будет яд, помечать их тоже надо единицами, чтобы восстановить картину. Комбинация погибших мышей из-за своей уникальности и укажет нам на номер пробирки с ядом.
Программисты и средняя оценка
— Да таким программистам надо премии выдавать!
— Им и выдают, только как-то странно. Смотрите сами.
Первый программист выполнил в марте 8 задач из 10, а второй — 5 из 6. Понятно, что 5/6 > 8/10. В апреле первый программист закрыл 4 задачи из 10, а второй — 6 из 14. Здесь тоже понятно, что 6/14 > 4/10. Но получается, что за два месяца у каждого из них было по 20 задач, и первый сделал 12, а второй 11. И второму начислили премию больше, чем первому. Как такое возможно: сделать больше задач за весь период, но проигрывать каждый месяц?
— Так ведь всё очень просто!
— Почему?
Всё противоречие здесь возникает оттого, что мы складываем задачи в одно целое и не учитываем степень нагрузки по ним.
Вместо этого нужно было складывать не отдельно общие задачи каждого программиста и количество выполненных из них, а дроби.
Если бы каждый из программистов выполнял норму в каждом месяце, то процент выполнения за 2 месяца был бы 200% — 100% за прошлый месяц и 100% за этот. Запомним это.
За март первый программист выполнил норму по задачам из трекера на 8/10, а за апрель — на 4/10. Теоретически он должен был сделать 20 задач, но сделал меньше. Получается, что всего за два месяца первый программист выполнил такую норму:
8/10 + 4/10 = 12/10 = 1,2
Умножим это на 100%, чтобы получить процент выполнения за 2 месяца у первого программиста:
1,2 × 100% = 120% из 200%.
Теперь посчитаем, как поработал второй программист. Для этого приведём дроби к общему знаменателю перед сложением:
5/6 + 6/14 = 70/84 + 36/84 = 106/84 = 1,26 из 2.
Умножим это на 100%, чтобы получить процент выполнения за 2 месяца у второго программиста:
1,2 × 100% = 126% из 200%
Это больше, чем тот же показатель у первого программиста. Поэтому у второго программиста премия больше.
Старые мониторы и лишняя тысяча
— О, у меня тоже была история с неправильным подсчётом, зацените.
Недавно решил перейти с двух мониторов на три и купить новые одинаковые, а старые продать. Прикинул, что они стоят 50 тысяч, и попросил знакомого помочь с продажей — у самого времени не было. А он продал их не за 50, а за 55 тысяч: каждый покупатель заплатил по 27 500 ₽ — на 2 500 ₽ больше, чем нужно.
И вот приходит ко мне этот знакомый и рассказывает о такой удачной продаже. Я попросил его вернуть по 2 500 ₽ каждому покупателю, но он снова схитрил — отдал им по тысяче, а три оставил себе. И вот знакомый считает: «26 500 + 26 500 = 53 000 — заплатили за мониторы, и ещё 3000 у меня осталось. Итого 53 000 + 3000 = 56 000. А продал я за 55 000. Любопытно».
— Ну и откуда взялась лишняя тысяча?
Ошибка в том, что знакомый складывал суммы от разных сделок. Правильные вычисления будут выглядеть так:
27 500 + 27 500 = 55 000 — получено после продажи мониторов
5000 — прежний владелец попросил вернуть покупателям, из них знакомый:
2000 — отдал
3000 — забрал себе
Как видим, лишней тысячи нигде нет.
Есть и другой способ: найти ошибку в вычислениях знакомого.
26 500 + 26 500 = 53 000 ₽ — заплатили покупатели за мониторы, хотя должны были заплатить 50 000 ₽, как хотел прежний владелец.
53 000 − 50 000 = 3000 ₽ — лишние деньги, которые знакомый и взял себе.
Ошибка в вычислениях в том, что нужно эти три тысячи не прибавлять, а отнимать, тогда получится нужная сумма в 50 000 ₽, которую получил прежний владелец мониторов.
Сложный выбор и гнутая монетка
— Хорошо посидели! Как же не хочется на работу… Может, взять выходной за свой счёт?
— Держи монетку, подбрось, и пусть рассудит случай.
— Но монетка погнута!
— И что?
— Из-за этого при подкидывании орёл с решкой будут выпадать не с одинаковой вероятностью: орёл выпадет в 2 раза чаще, чем решка. Если поставить выходной на орла, у него будет больше шансов.
— Ну тогда подкинь монетку больше одного раза, и вот тебе гарантированный способ получить равные шансы.
— Какой?
Из-за того, что одна сторона выпадает чаще другой, мы не можем использовать одно подкидывание для определения, идти на работу или взять выходной. Но что, если подбросить монету не один, а два раза подряд? Смысл в том, чтобы найти такие комбинации, которые дают равные шансы на победу.
Если подкинуть монетку два раза, то у нас получатся такие варианты:
- Орёл — Орёл (ОО)
- Орёл — Решка (ОР)
- РО
- РР
Первый вариант мы отбрасываем сразу — у него самый высокий шанс выпадения. Вариант с двумя решками тоже не подходит — он выпадет реже всего.
Теперь посмотрим, что с шансами выпадения сначала орла, а потом решки и наоборот. Для этого перемножим вероятности выпадения орла (2/3) и решки (1/3) в разной очерёдности:
ОР: ⅔ × ⅓ = 2/9
РО: ⅓ × ⅔ = 2/9
Получается, что у обеих этих последовательностей одинаковый шанс выпасть при двойном броске монеты. Это значит, что выход на работу можно поставить на последовательность ОР, а выходной — на РО. Если же выпадет ОО или РР, то мы просто перебросим монетку ещё два раза.
