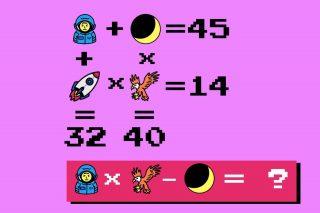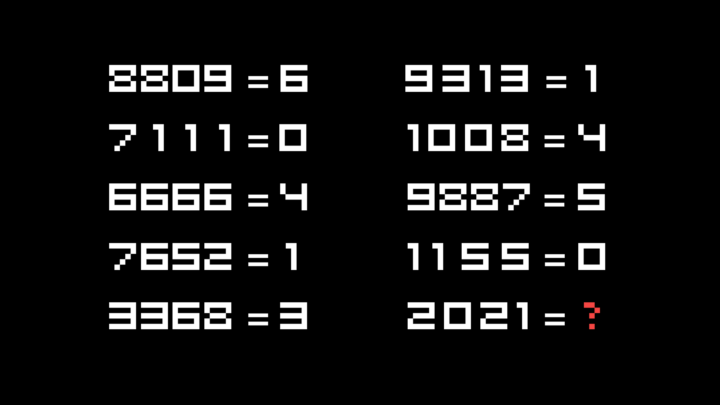Космическая задача из NASA
Картинки — это целые положительные числа. Нужно найти эти числа:
👩🚀 + 🌒 = 45
+ ×
🚀 × 🦅 = 14
= =
32 40
👩🚀 × 🦅 − 🌒 = ?
Так как за красивыми иконками скрываются какие-то неизвестные числа, то и относиться к этим иконкам мы будем как к простым неизвестным.
Для начала возьмём два умножения:
🌒 × 🦅 = 40
🚀 × 🦅 = 14
Вычтем одно из другого и вынесем орла за скобки:
🌒 × 🦅 − 🚀 × 🦅 = 40 − 14
🦅(🌒 − 🚀) = 26
Запомним это и теперь возьмём два сложения:
👩🚀 + 🌒 = 45
👩🚀 + 🚀 = 32
Тоже вычтем из первого второе и посмотрим, что получится:
👩🚀 + 🌒 − (👩🚀 + 🚀) = 45 − 32
👩🚀 + 🌒 − 👩🚀 − 🚀 = 13
🌒 − 🚀 = 13
Теперь подставим это значение в наш первый результат с умножением:
🌒 − 🚀 = 13
🦅(🌒 − 🚀) = 26
🦅 × 13 = 26 → 🦅 = 2
Зная это, подставим орла в первые два умножения:
🌒 × 2 = 40 → 🌒 = 20
🚀 × 2 = 14 → 🚀 = 7
А теперь подставим луну в первую сумму, чтобы найти, чему равен астронавт:
👩🚀 + 🌒 = 45
👩🚀 + 20 = 45 → 👩🚀 = 25
Итак, когда мы знаем все значения, то легко сможем найти итоговый результат:
👩🚀 × 🦅 − 🌒 = 25 × 2 − 20 = 30
Задача про умножение с нестандартным решением
У этой задачи есть два решения — одно рассчитано на детей, второе — на взрослых. Какое сможете найти вы?
Сама задача выглядит так. Надо найти, чему равны A и B:
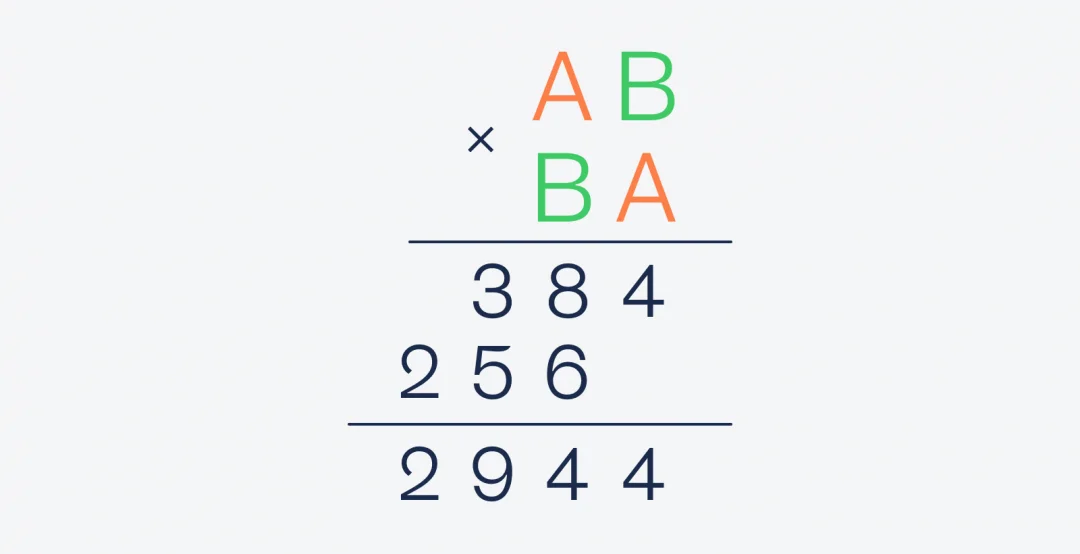
Представим, что мы знаем только самое простое умножение, максимум — с двузначными числами. Начнём с самого первого действия умножения в столбик:
AB × A = 384
Так как AB — это A × 10 + B, то если разделить AB на 10, то получим число A,B. Получается, что A,B × A = 38,4 (потому что первую строку мы тоже делим на 10.
А теперь следите за логикой. Это число — 38,4 — близко к квадрату числа A (A × A), и погрешность вносит только дробная часть. Представим, что её нет и посмотрим, квадрат какого числа максимально близко к 38,4:
5 × 5 = 25 → нет, слишком мало
6 × 6 = 36 → похоже на правду
7 × 7 = 49 → не, уже перебор
Получается, что число A — это 6. Зная это, подставим пока ноль вместо числа B и посмотрим, что получится:
60 × 6 = 360
Но у нас на второй строке стоит 384. Это значит, что B × 6 = 384 − 360 = 24. Получается, что B = 4.
Проверяем: 64 × 46 = 2944. Всё сходится, а значит, мы решили всё правильно.
Если мы будем решать эту задачу как программисты, то сразу заметим число 256 и вспомним, что 256 = 2 в восьмой степени. Это значит, что все его множители будут кратны двойке:
128 × 2
64 × 4
32 × 8
16 × 16
Число 256 получилось из умножения AB × B, то есть двузначного числа на однозначное. Из всех наших пар 128 × 2 не подходит, потому что 128 — трёхзначное число. И 16 × 16 тоже не подходит, потому что в этом случае мы умножаем не на однозначное, а на двузначное число.
Остаются пары 64 × 4 и 32 × 8. Но шаблону AB × B соответствует только пара 64 × 4, а значит, A = 6, а B = 4.
Для нетерпеливых есть решение, которое можно запустить и протестировать прямо в консоли:
- Создаём цикл для переменной a, где мы перебираем значения a от 0 до 9.
- Внутри него такой же вложенный цикл для переменной b.
- Внутри этого вложенного цикла собираем два числа и перемножаем их. Чтобы собрать число ab, нужно a умножить на 10 и прибавить b. Аналогично для числа ba. Перемножаем их и сравниваем с искомым 2944.
- Если сравнение случилось, выводим результат в консоль.
Итоговый код на JavaScript:
for (var a = 0; a <= 9; a++) {
for (var b = 0; b <= 9; b++) {
if ((a*10+b)*(b*10+a)==2944) {console.log(""+a+b+" * "+b+a+" = 2944")};
}
}Можете скопировать, вставить в консоль браузера и проверить. Результат будет таким:
46 * 64 = 2944
64 * 46 = 2944
Что должно стоять вместо цветных шаров?
Эта задача входит в некоторые сборники тестов, которые показывают уровень IQ и умение быстро принимать верные решения. Эти качества пригодятся любому программисту, поэтому вот вам задача:
За 60 секунд найти цифры, которые должны стоять вместо шаров. Одинаковые цвета означают, что на этих местах стоят одинаковые цифры:
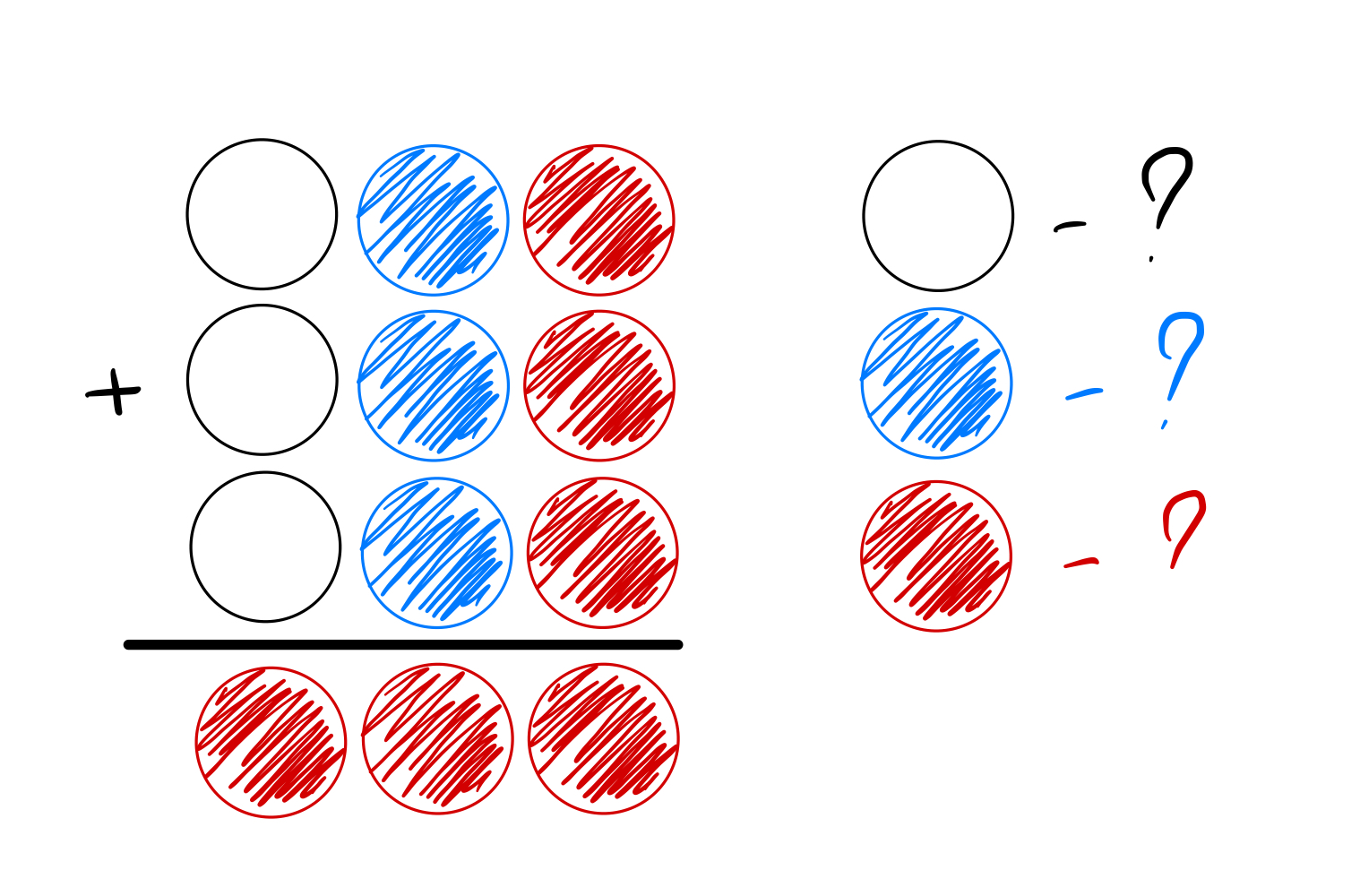
Чтобы решить эту задачу действительно за 60 секунд, сразу обращаем внимание на красный столбик:
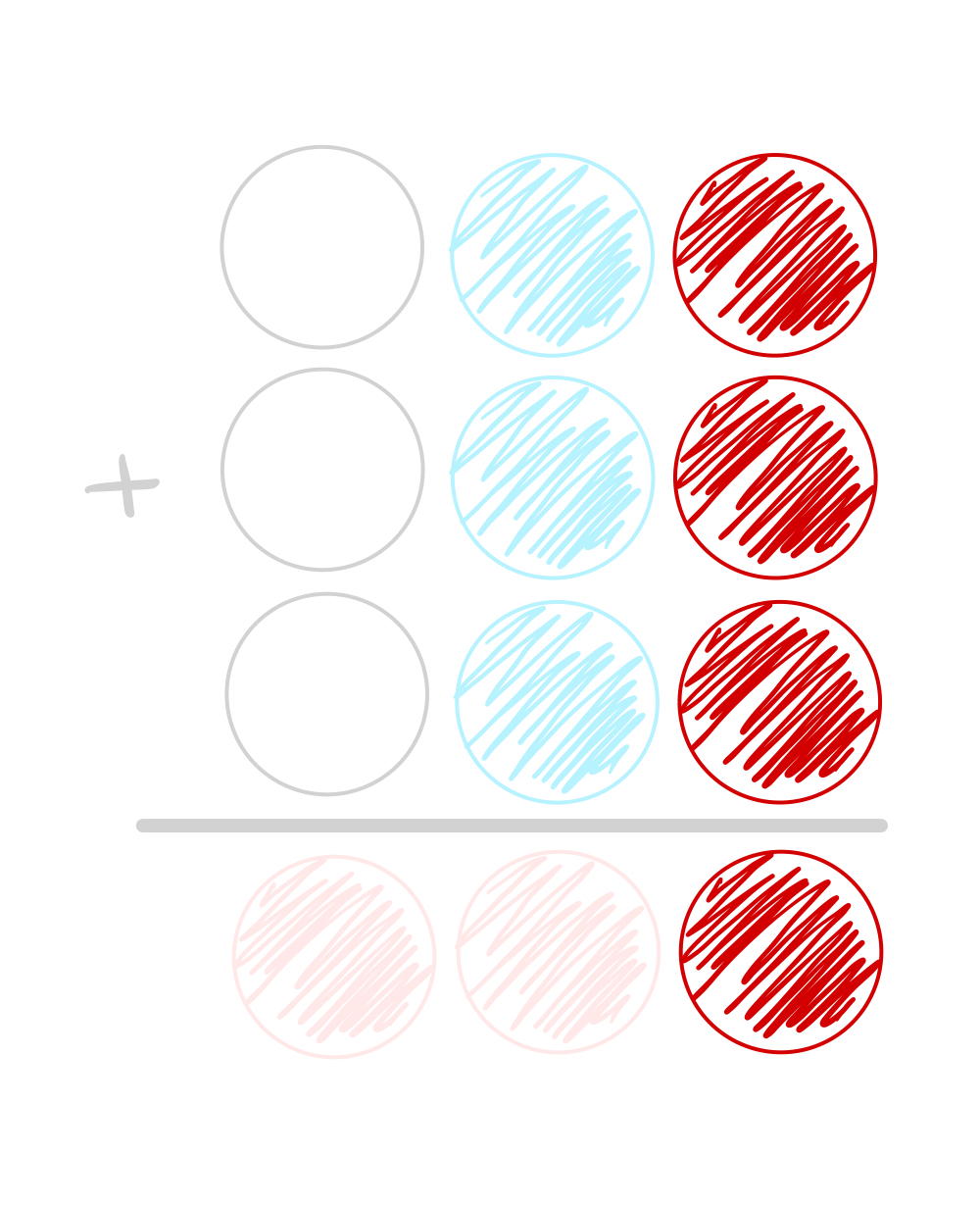
Глядя на рисунок, мы понимаем, что при сложении трёх одинаковых чисел мы получим какое-то число, которое также заканчивается на эту же цифру. Можно построить несложные математические выкладки для решения этой части, а можно решить «в лоб» и просто посмотреть, какие числа от 0 до 9 дают такой эффект:
3 × 0 = 0
3 × 1 = 3
3 × 2 = 6
3 × 3 = 9
3 × 4 = 12
3 × 5 = 15
3 × 6 = 18
3 × 7 = 21
3 × 8 = 24
3 × 9 = 27
У нас получились числа 0 и 5, которые при сложении три раза подряд дают в конце результата тоже 0 или 5. Но 0 не подходит, потому что тогда у нас ответ тоже станет 000, а это значит, что белый и синий шары тоже равны нулю, а по условию разные цвета — это разные цифры:
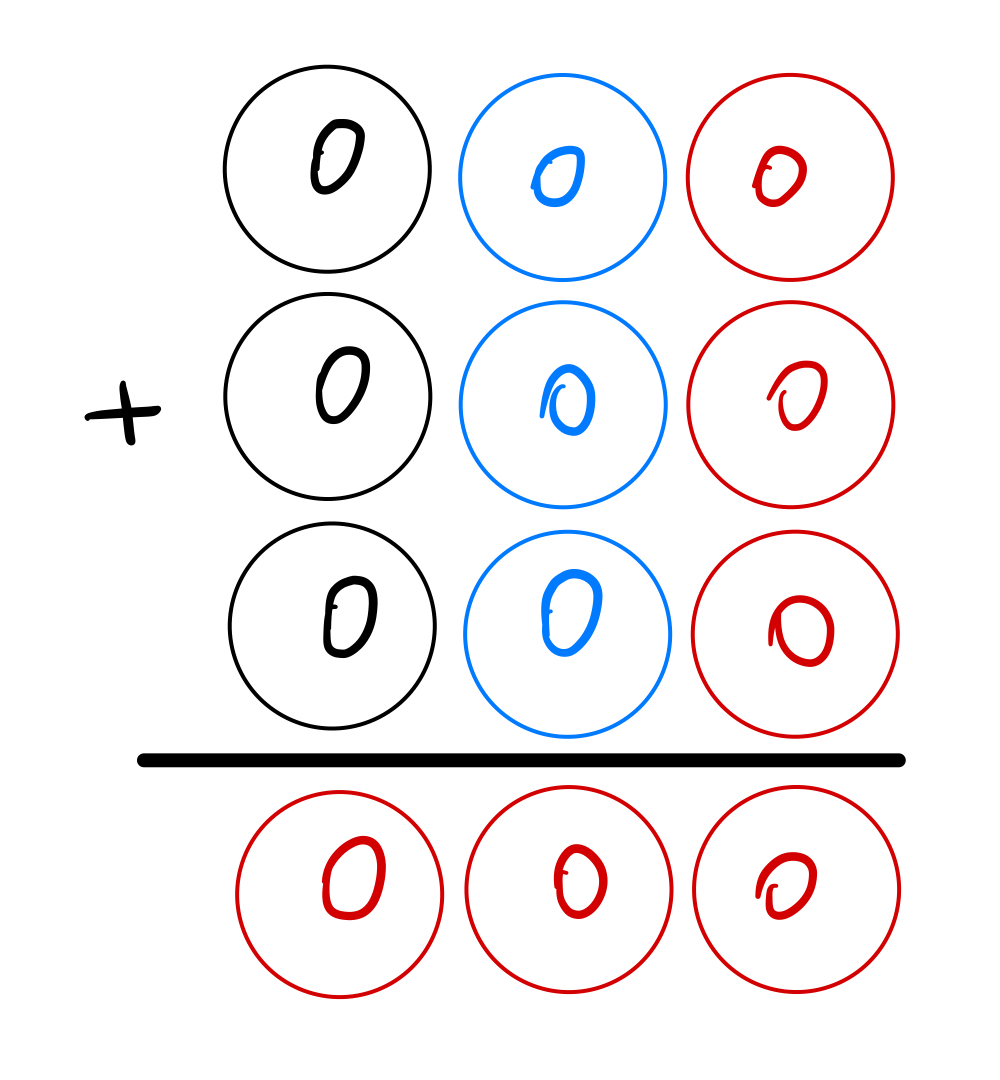
Получается, что вместо красного шара должна стоять цифра 5:
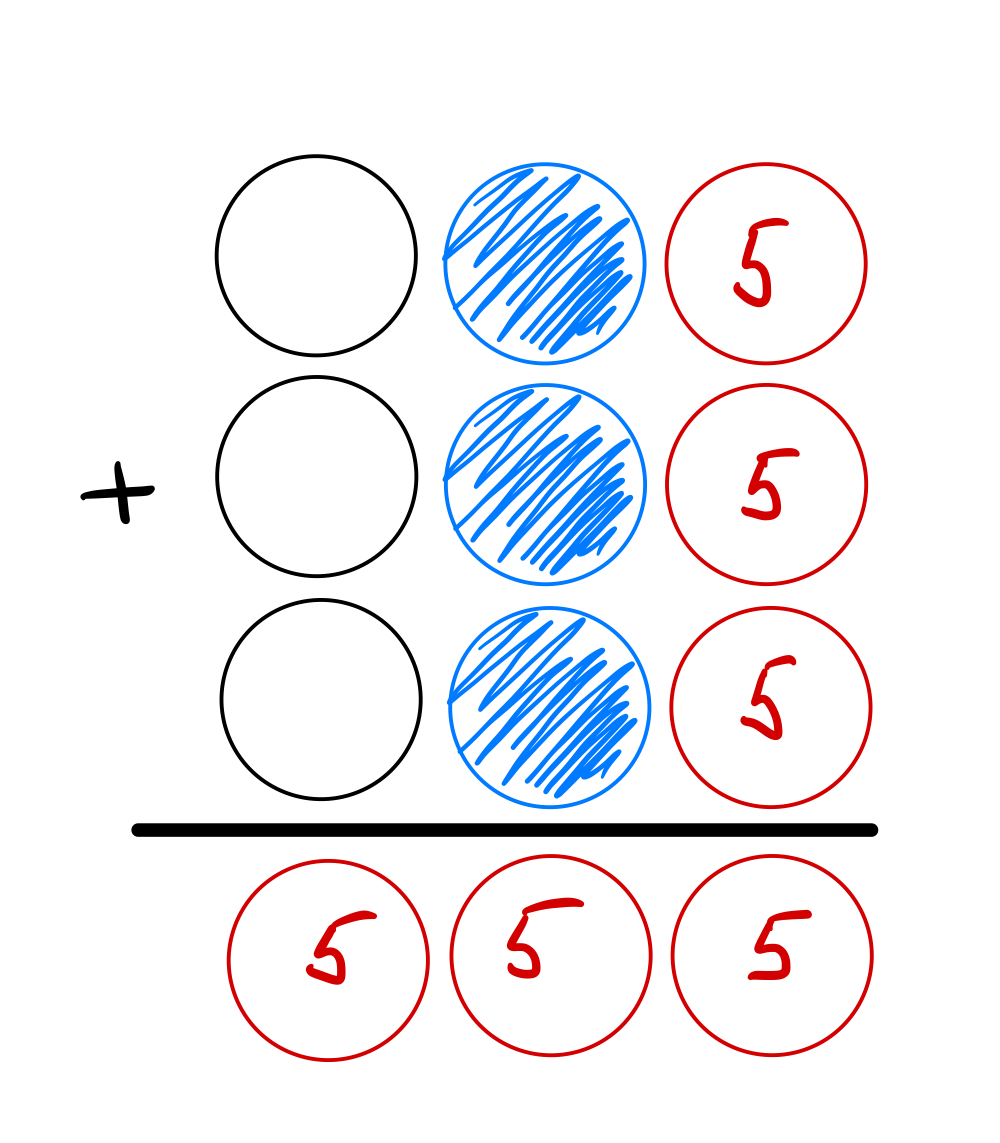
Но раз у нас складываются три одинаковых числа, а в ответе 555, то логично разделить 555 на 3, чтобы найти это число: 555 / 3 = 185:
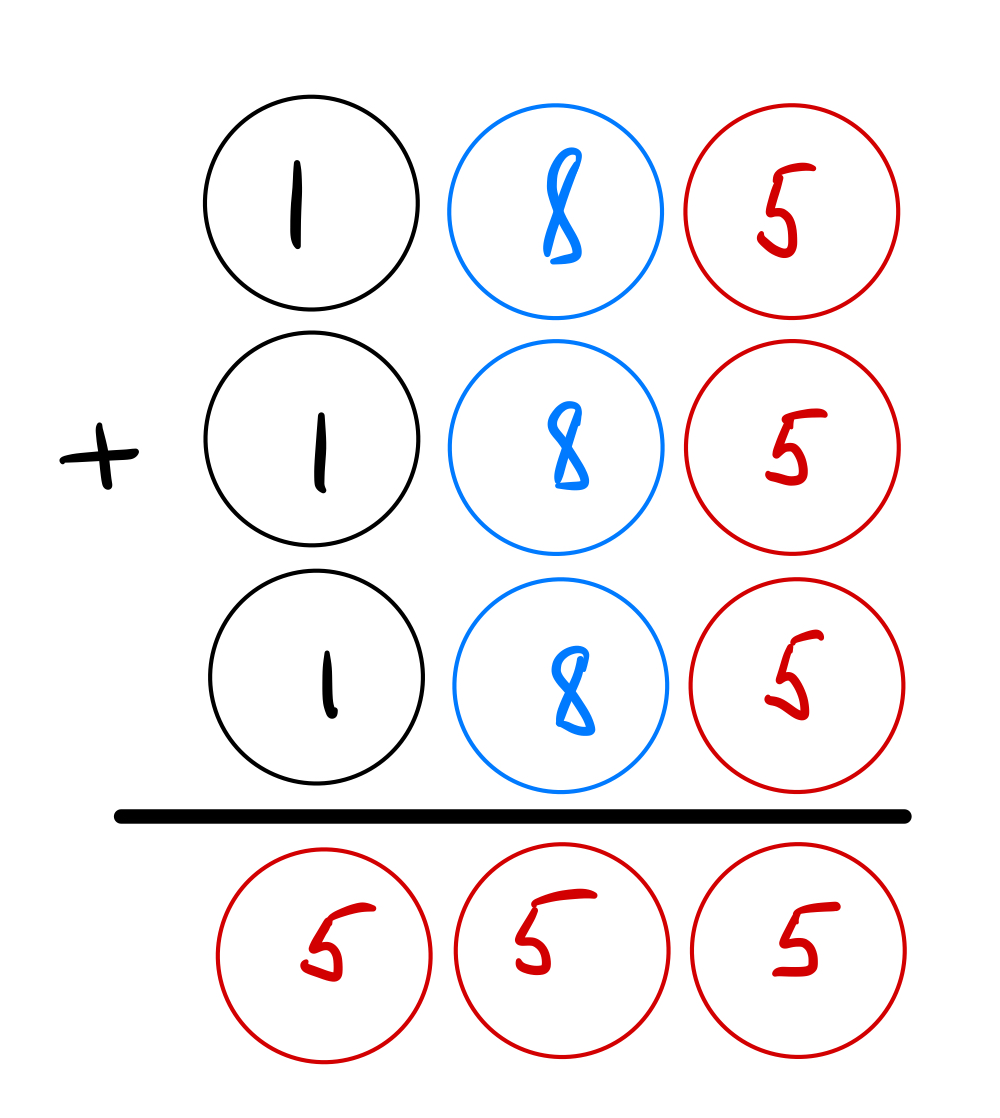
Если вы смогли решить эту задачу так же быстро — поздравляем, можно смело приходить в Практикум и выбирать новую профессию в ИТ!
Сколько стоит флешка?
Одна предприимчивая бабушка после продажи домашних помидоров и изюма решила открыть магазин электроники, и у неё состоялся с покупателем такой диалог:
— Здравствуйте, мне нужна флешка, блок питания для зарядки телефона и мышка.
— С вас 216 рублей.
— А сколько стоит блок питания?
— Три блока питания стоят столько же, сколько мышка и флешка вместе.
— Хм, а флешка тогда сколько стоит?
— Как в сумме два блока и две мышки.
— Отлично, — сказал покупатель, — тогда мне просто две флешки, — и протянул бабуле 300 рублей.
Сколько сдачи должна дать бабуля за две флешки?
Несмотря на то что единственное число, которое нам известно, — это общая сумма за флешку, блок питания и мышку, эту задачу можно решить за пару минут. Всё, что нам нужно сделать, — записать в виде уравнений все условия, которые нам известны.
Обозначим наши переменные с помощью эмодзи, чтобы быстрее всё двигать:
Флешка → 💾
Блок питания для зарядки → 🔌
Мышка → 🐭
Запишем всё, что нам известно. Все три предмета в сумме стоят 216 рублей:
💾 + 🔌 + 🐭 = 216
Три блока для зарядки стоят столько же, сколько мышка и флешка вместе:
💾 + 🐭 = 🔌🔌🔌
А флешка стоит как две зарядки и две мышки:
🔌🔌 + 🐭🐭 = 💾
Теперь мы можем работать с этими тремя уравнениями по стандартным математическим правилам. Если посмотреть на первое и второе уравнение, то и там и там в левой части есть флешка и мышка. Получается, что мы можем в первое уравнение (💾 + 🔌 + 🐭 = 216) подставить три зарядки вместо флешки с мышкой (💾 + 🐭 = 🔌🔌🔌):
🔌🔌🔌 + 🔌 = 216
4 × 🔌 = 216
🔌 = 216 / 4 = 54
Мы выяснили, сколько стоит одна зарядка. Подставим это значение во все остальные уравнения:
💾 + 🐭 = 🔌🔌🔌 → 💾 + 🐭 = 162
🔌🔌 + 🐭🐭 = 💾 → 108 + 🐭🐭 = 💾
У нас по одной флешке в каждом уравнении — используем это:
💾 + 🐭 = 162 → 💾 = 162 − 🐭 ← подставим это вместо флешки в последнее уравнение:
108 + 🐭🐭 = 162 − 🐭
🐭🐭🐭 = 162 − 108 = 54
🐭 = 18
Мы знаем, сколько стоит блок и мышка, — подставим эти значения в самое первое уравнение, чтобы найти, сколько стоит флешка:
💾 + 54 + 18 = 216
💾 = 216 − 54 − 18
💾 = 144
А раз одна флешка стоит 144 рубля, то две будут стоить 288 рублей. Это значит, что бабушка должна дать 300 − 288 = 12 рублей сдачи.
Какой сегодня день недели? Когда выходной?
Сисадмин спросил у начальника, когда тот сможет дать ему выходной, на что получил такой ответ:
🤔 Когда послезавтрашний день станет вчерашним, то выходной будет так же далеко от субботы, как тот день, который был сегодня, когда позавчера было завтра.
Сисадмин сначала задумался, а потом пошёл за пивом. Что он понял?
Начальник специально запутал все дни недели, чтобы сисадмину было над чем подумать. Всё, что нам нужно сделать, — это последовательно разобраться в днях и посчитать, сколько дней нужно прибавить или отнять от субботы.
Сначала решим первую часть: «Когда послезавтрашний день станет вчерашним». Обозначим сегодняшний день за X, тогда завтрашний день становится X+1, а послезавтрашний — X+2. Чтобы день X+2 стал вчерашним, должен наступить новый день — X+3.
Теперь разберёмся со второй частью: «как тот день, который был сегодня, когда позавчера было завтра». Раз X — это сегодня, то вчера был день X−1, а позавчера — X−2. Чтобы какой-то день стал «завтра», нам нужно вернуться ещё на один день назад, поэтому, когда «позавчера было завтра» — это X−3.
Объединим первую часть (X+3) и вторую (X−3). Получается, что через 3 дня «выходной будет так же далеко от субботы», как и 3 дня назад. Тогда, в какую бы сторону мы ни двигались от изначального дня (субботы), мы уйдём на одно и то же количество дней. А это значит, что суббота и есть наш искомый день недели и что выходной у сисадмина будет в субботу.
Как пел классик авторской песни Гуф, «Ведь сегодня завтра будет вчера; а ещё вчера сегодня было завтра».
Как вычислить день рождения
👉 Чтобы закрыть тему с математическими фокусами, мы приготовили напоследок трюк с датой рождения. Примерно по таким алгоритмам работают все фокусы с числами: сколько бы действий ни пришлось выполнить, результат давно просчитан и не требует от фокусника никакой магии. Поэтому просто почитайте, как это работает.
Этот несложный математический трюк поможет узнать вам дату рождения кого угодно, даже если это ваше первое свидание. Если вы в кафе заказали поесть, а заказ ещё не принесли — самое время откинуться на спинку стула и сказать такое:
— Давай покажу тебе одну хитрую штуку! Для этого умножь число своего рождения на 2, но мне не говори. Как умножишь — прибавь туда 5, а потом результат умножь на 50. Ну и напоследок, чтобы было ещё хитрее, прибавь к этому номер месяца из своей даты рождения.
— 1555.
— У тебя день рождения 13 мая!
— Как ты это сделал ? О_о
Так как в любом фокусе с числами всё основано на чистой математике и формулах, мы пойдём тем же путём: обозначим день рождения за X, а месяц — за Y.
Выполним все действия по очереди:
- Умножаем день на 2: X × 2.
- Прибавляем 5: X × 2 + 5.
- Умножаем на 50: (X × 2 + 5) × 50 = 100X + 250
- Прибавляем номер месяца: 100X + 250 + Y.
Если выкинуть отсюда 250, то у нас получится 100X + Y — только те числа, которые связаны с датой рождения. А теперь смотрите, что получается дальше.
Независимо от того, чему у нас равен икс, если мы его умножим на 100, то в конце числа у нас будет два ноля, а в начале — сам день рождения (день, без месяца). Это значит, что если мы отбросим последние два числа, то получим снова день рождения.
Например, если день рождения 13 мая, то 13 × 100 = 1300 → отбрасываем последние два числа и снова получаем 13.
Но раз у нас в конце стоят два ноля, то что бы к ним двузначного ни прибавили, получим то же самое число. Количество месяцев у нас всегда двузначное, поэтому они не смогут повлиять на третий разряд в итоговом числе.
Получается, что в формуле 100X + Y последние два числа — это номер месяца в дате рождения, а остальное, что в начале — это день.
Проверим на дате 13 мая: 13 × 100 + 5 = 1305. Последние два числа — это месяц (05), а что осталось спереди — это день (13).
Но всё это у нас получается, если откинуть от итогового результата 250. Значит, когда вам называют итоговое число, то от него нужно отнять 250, а потом разложить ответ на составляющие: месяц (2 последние цифры) и день (всё остальное спереди).