Нерадивый эйчар получил задание прособеседовать двоих кандидатов на должность аналитика. Он случайно назначил две встречи на одно время, кандидаты пришли. Ну и глупо: не будешь же ты их собеседовать одновременно.
Эйчар сделал вид, что всё так и задумано, и предложил кандидатам интеллектуальный поединок. Он быстро на бумажке что-то посчитал, а потом сказал:
- Предлагаю вам решить вот это уравнение с двумя неизвестными.
- Неизвестные m и n — целые положительные числа.
- Кто даст правильный ответ первым, тот проходит на следующий этап собеседования.
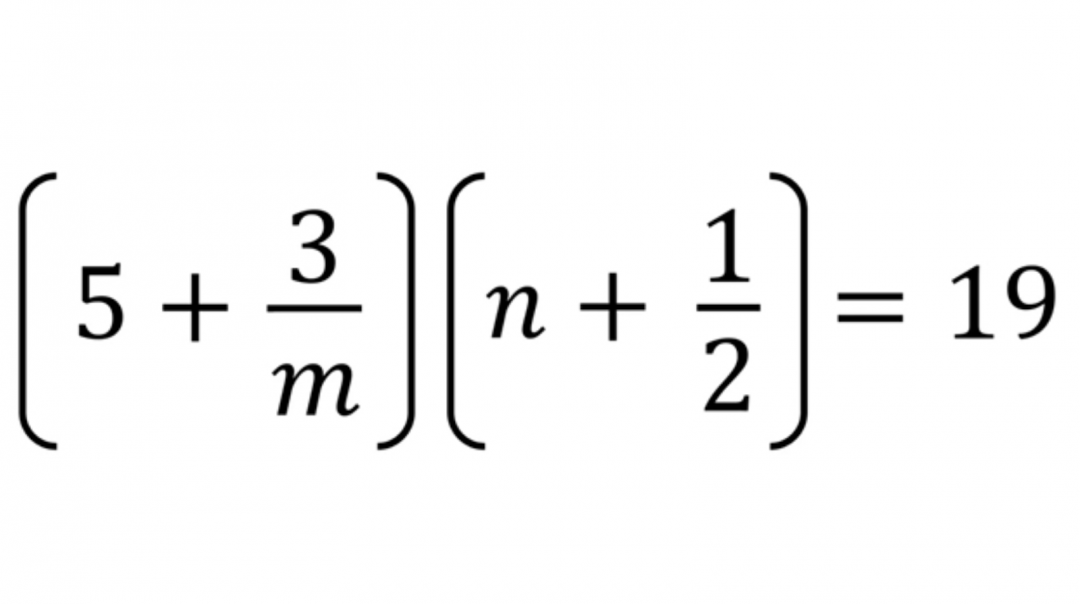
Один аналитик решил блеснуть своими навыками автоматизации. Он открыл ноутбук и стал писать программу, которая мгновенно нашла бы нужные корни.
А второй закатил глаза, написал на листке ответ, отдал его эйчару и красиво ушёл. И вот эйчар сидит и не понимает, как второму это удалось. А правда, как?
Есть два стандартных подхода к решению этого уравнения: алгебраическое и через сравнения соотношений. Оба требуют обстоятельных разъяснений каждого действия.
Но есть и третье решение, которое намного проще — нужно лишь внимательно посмотреть на формулу и подключить здравый смысл. Так и сделаем.
- У нас есть два выражения в скобках, произведение которых даёт 19.
- В первых скобках число точно больше 5, потому что там сумма пяти с чем-то другим.
Если мы разделим 19 просто на 5, то получим 3,8 — это самое большое, что может быть во вторых скобках, потому что чем больше значение в первых скобках, то тем меньше значение во вторых.
Самое большое значение, которое может быть в первых скобках — 8, когда m = 1. Это значит, что самое маленькое значение во вторых скобках — 19 / 8 = 2,375.
🤔 Получается, что значение вторых скобок лежит в диапазоне от 2,375 до 3,8.
Так как в скобках прибавляется 1/2, то отнимем её и от вторых скобок, и от диапазона. Получается так:
1,875 > n > 3,3
Единственные два целых числа, которые сюда подходят — это 2 и 3. Проверим их по очереди, подставив в исходное уравнение.
Если n = 2, то вторые скобки равны 2,5, и получается, что:
(5 + 3/m) × 2,5 = 19
5 + 3/m = 7,6
3/m = 2,6 → m = 1,15. Но так быть не может — по условию числа должны быть целыми.
Значит, остаётся только n = 3. Давайте проверим:
(5 + 3/m) × (3 + ½) = 19
(5 + 3/m) × 3,5 = 19, но 3,5 — это 7/2, поэтому (5 + 3/m) × (7/2) = 19
5 × 3/m = 19 / (7/2) = (19 × 2) / 7 = 38/7
3/m = 38/7 - 5 = 38/7 - 35/5 (потому что 5 = 35/7)
3/m = 3/7 → m = 7
Вот мы и нашли ответ без второго уравнения: m = 7, n = 3.
Короче: секрет был в том, чтобы обратить внимание на число 5 и условия задачи.