Интеграл в математике: что это и как его понять

Недавно мы разобрали, что такое знаки Σ и П в математике — это операции, которые, по сути, похожи на циклы в программировании. В одном случае мы складывали много чисел по определённому принципу, а в другом — умножали. 

Сегодня посмотрим на интеграл ∫ — что это такое и какой цикл можно сделать из него. 

Но сначала: что такое функция

Интегралы в математике всегда связаны с функциями, поэтому сначала поговорим про них. 

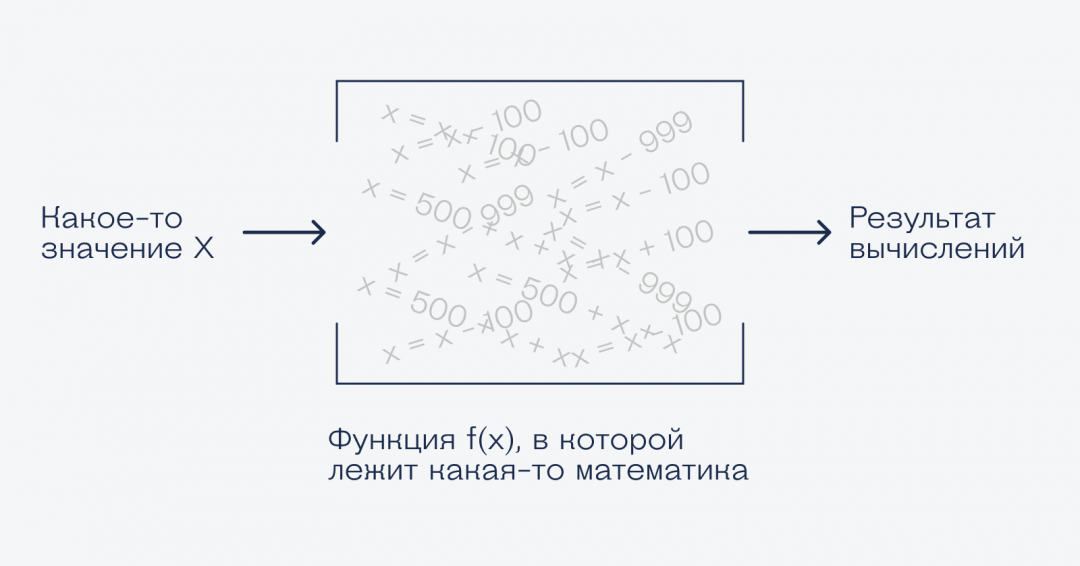
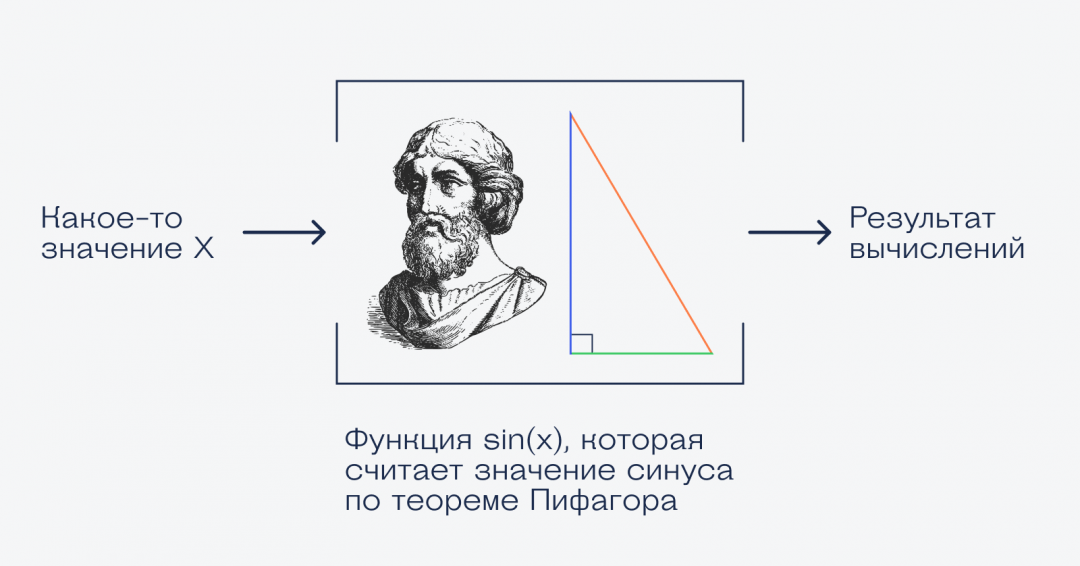
Функцию можно представить как «коробку с математикой». У тебя есть какая-то масса математических операций, ты их «запаковываешь» в функцию. Теперь ты можешь эту массу операций вызывать в своих математических выражениях одним действием. 

У функции есть один или несколько аргументов — это те числа, к которым нужно применить массу математических операций. Можно представим, что мы засунули это число в коробку с математикой, потрясли и получили на выходе другое число. 

Из школы вы наверняка помните функции sin() и cos() — синус и косинус. На вход им подаётся какое-то число, это число насилуют по теореме Пифагора, а на выходе получается дробное число от –1 до 1. 

Функции можно засовывать в другие функции. Например, возьмём новую функцию f(x) и положим в неё выражение sin(x) + cos(x). Это будет работать так: 

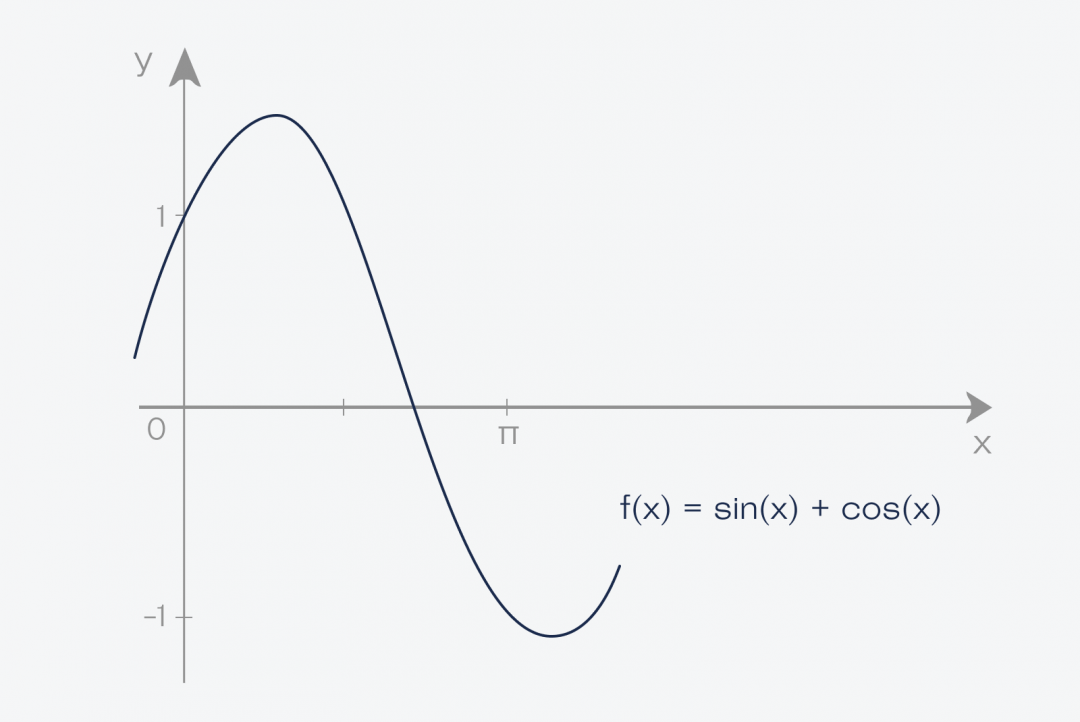
Если посчитать f(x) для одного числа, получится другое число. Если посчитать f(x) от 100 чисел, получится 100 других чисел. А если непрерывно считать f(x) для бесконечного количества чисел, то получится бесконечное количество других чисел. 

Если поставить эти числа по возрастанию x, то можно построить график функции y = f(x). Это означает, что по горизонтали мы имеем все возможные значения x, а по вертикали — результат вычисления функции f(x). Если каждый результат отметить точкой, получится линия: 

Что такое интеграл

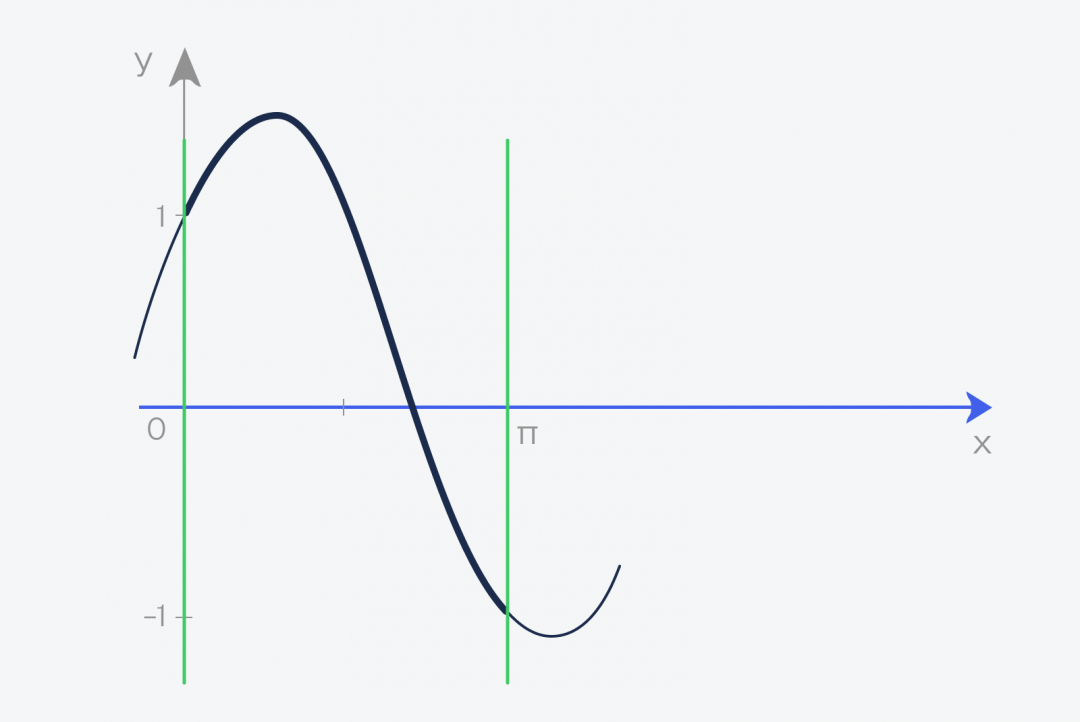
Итак, у нас есть некая функция, у неё есть числа на входе и числа на выходе. Эти пары чисел можно использовать для построения графика функции. 

Теперь берём этот график функции и проводим две линии, которые ограничивают график. Получается фигура, которая сверху зависит от нашей функции, а с остальных сторон ограничена прямыми линиями и осью:

А теперь то, ради чего всё это затевалось:

В нашем случае мы считаем интеграл от нуля до числа пи — 3,1415926...

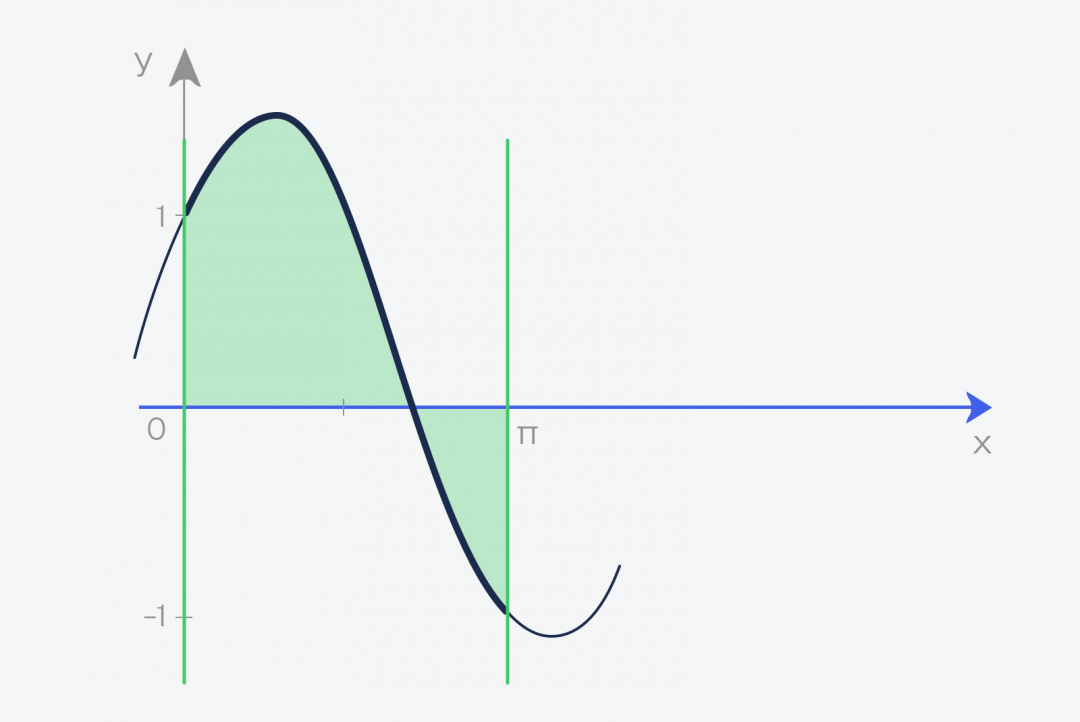
Это называется определённый интеграл. Определённый — это когда у нас определены начало и конец фигуры — в математике это называют пределами интегрирования. Записывается этот интеграл так:

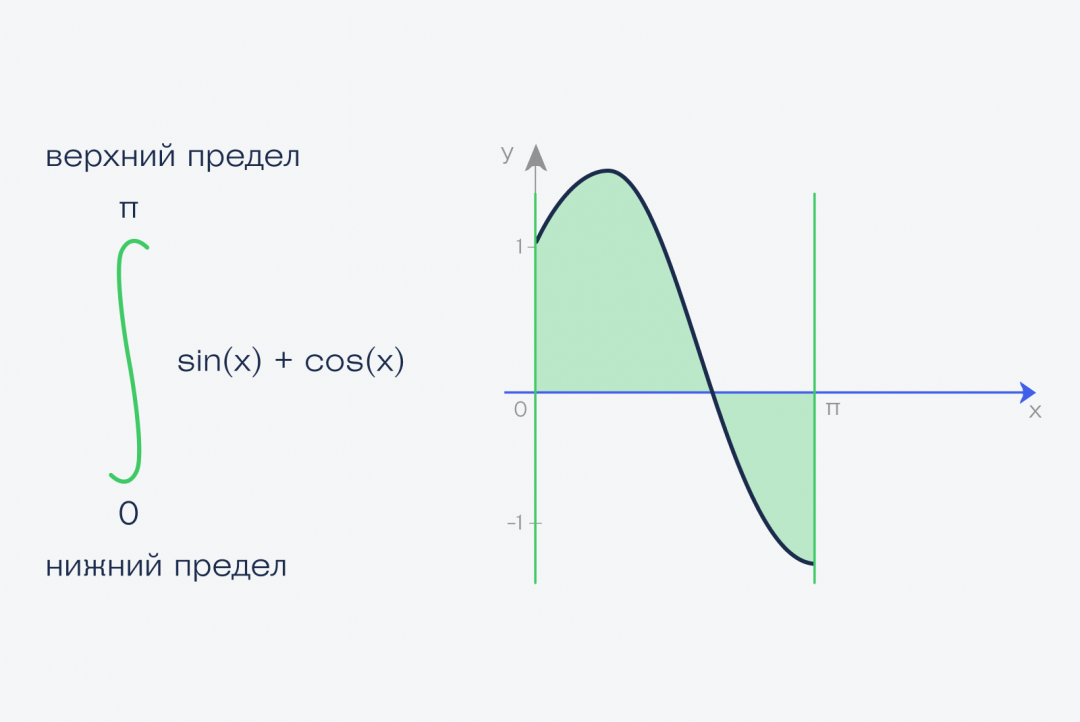
В математике есть ещё неопределённые интегралы, у которых нет пределов интегрирования. Ими мы заниматься не будем, потому что ответом к неопределённому интегралу будет не конкретное число, а формула.

Зачем нужны интегралы в народном хозяйстве

Вы удивитесь, но в первую очередь интегралы нужны, чтобы находить площади и объёмы. В буквальном смысле: вот фигура, вот её описание в виде функции, проинтегрировали — узнали площадь. Будете, например, заливать бетоном красивую кривую дорожку — узнаете, сколько вам нужно бетона. 

Интегралы нужны в математике и физике, это один из инструментов вычислений.

Если вы астрофизик, интеграл поможет вам рассчитать какие-нибудь свойства звёзд с течением времени. А математики говорят, что в интегралах не нужно искать практический смысл; их нужно любить, как мать, и почитать, как отца. 

Как посчитать интеграл (то есть найти площадь)

Если бы у нас был прямоугольник, то всё просто: перемножаем высоту на ширину. Если бы была трапеция, тоже ещё как-то что-то можно. Но сверху у нас кривая, поэтому так сделать не получится. Решение придумали такое:

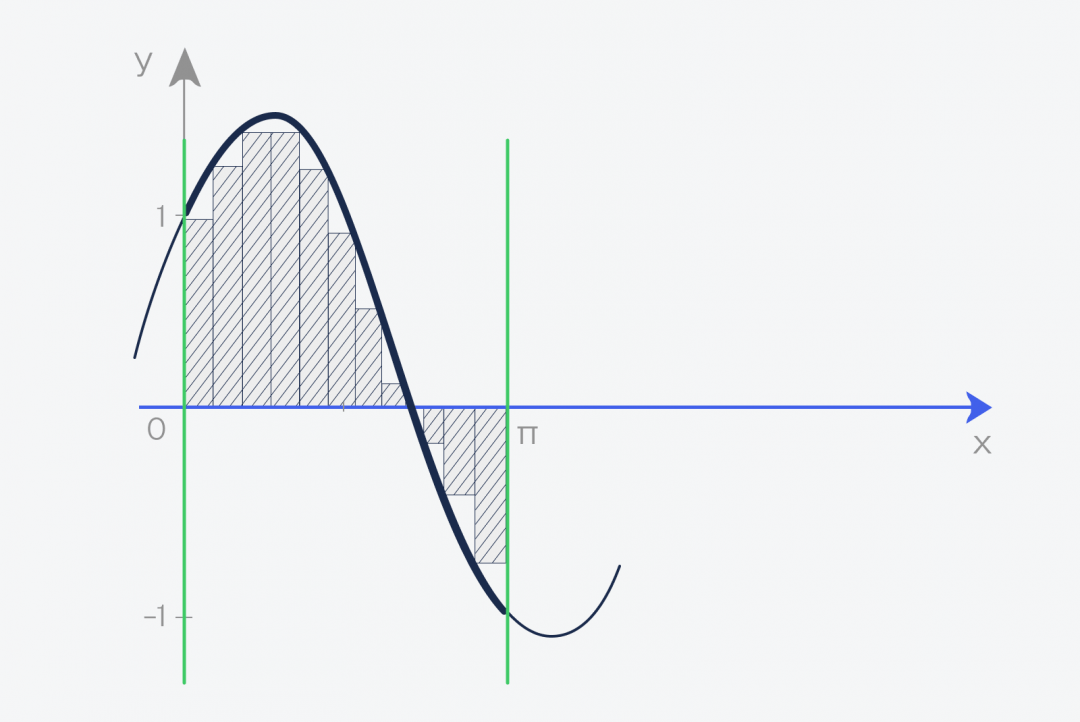
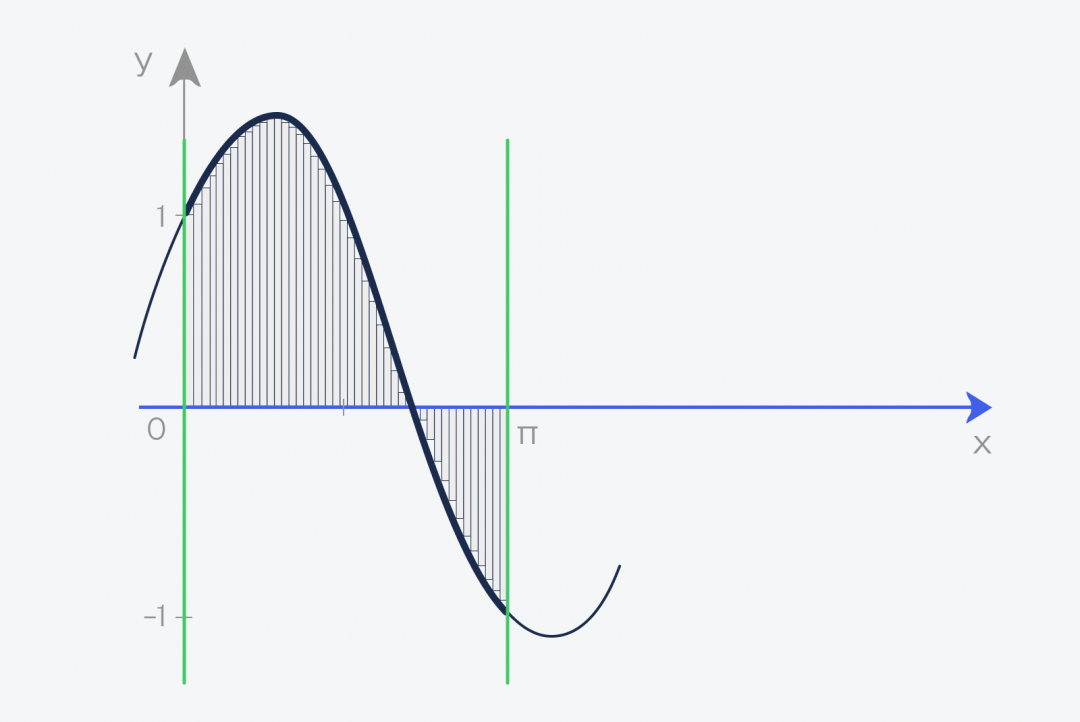
Минус такого подхода в том, что, как бы мы ни старались, прямоугольники не могут повторить все изгибы, и появится погрешность. С другой стороны, чем тоньше будут эти прямоугольники, тем точнее будет ответ. Получается, что наша задача — нарезать фигуру как можно тоньше.

Теперь задача становится намного проще: мы просто считаем площадь каждого прямоугольника и складываем их вместе. В таком виде задачу уже можно решить простым алгоритмом.

Пишем код

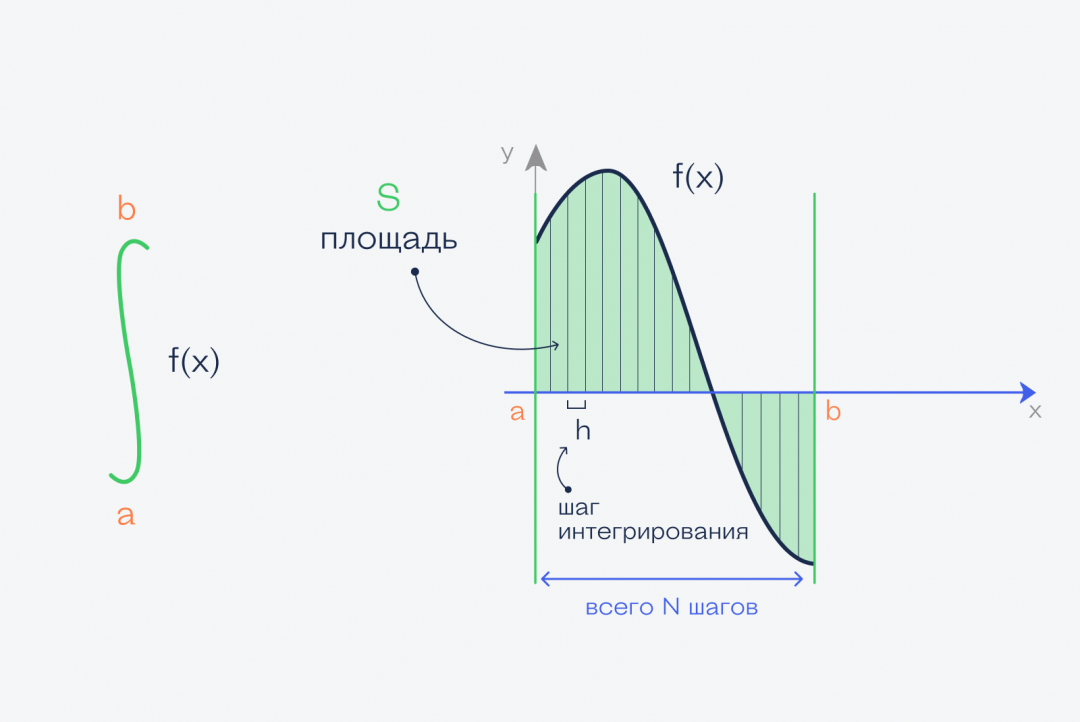
Раз нам нужно разбить интервал на много частей а потом с каждой из них сделать одно и то же, то это точно задача для цикла. Для этого нам понадобится шаг цикла — какой ширины будут наши прямоугольники, чтобы бы могли их одинаково перебирать.

Чтобы посчитать шаг, находим расстояние между конечной и начальной точкой и делим на желаемое количество прямоугольников (это будет нашей точностью интегрирования).

 Общая логика работы будет такая:

На картинке — все исходные данные, а ниже — код, который считает интеграл. Смотрите на картинку и читайте комментарии: так будет ещё проще разобраться в коде:

// задаём границы интегрирования
// считать будем от нуля до пи
var a = 0;
var b = 3.1415926;

// задаём точность вычислений, на сколько частей будем делить интервал
n = 10000;

// шаг интегрирования (оно же — ширина мини-прямоугольника. Пока что пустая переменная, мы её посчитаем.)
var h;

// текущее значение переменной для функции
// на старте оно совпадает с первой границей
var current = a;

// здесь будем хранить значение получившегося интеграла
var s = 0;

// функция, которую нужно проингтегрировать
function f(x) {
	return (Math.sin(x) + Math.cos(x));
}

// считаем шаг интегрирования
h = (b - a)/n;

// пока не дошли до другой границы — цикл работает
while (current <= b){
	// находим значение функции в текущей точке и умножаем его на значение шага
	// так мы получим площадь очень маленького прямоугольника, который можно нарисовать в этой точке
	// общая площадь фигуры — это сумма всех таких маленьких прямоугольников
	s = s + (f(current) * h );
	// сдвигаемся к следующей точке
	current += h;
}

// должно получиться число 2 или что-то очень близкое к нему
console.log('Значение интеграла: ' + s);

Что дальше

Теперь этот код можно изменить так, чтобы он считал интеграл в любых пределах у любой функции. С точки зрения математики это не самый точный результат, но всё зависит от того, сколько точных знаков после запятой нам нужно. 

В следующей серии продолжим разбираться со страшной математикой. Если есть пожелания для разбора — напишите в комментариях.

Любите данные? Посмотрите вот это

Возможно, у вас получится построить карьеру в мире дата-сайенса. Это новое направление, в котором очень нужны люди. Изучите эту сферу и начните карьеру в ИТ: старт — бесплатно, а после обучения — помощь с трудоустройством.

Начать бесплатно