По пятницам у нас иногда задачки на логику, математику и геометрию. Кто решит в уме или на листочке, тот, считай, прошёл первый этап собеседования в ИТ-компанию.
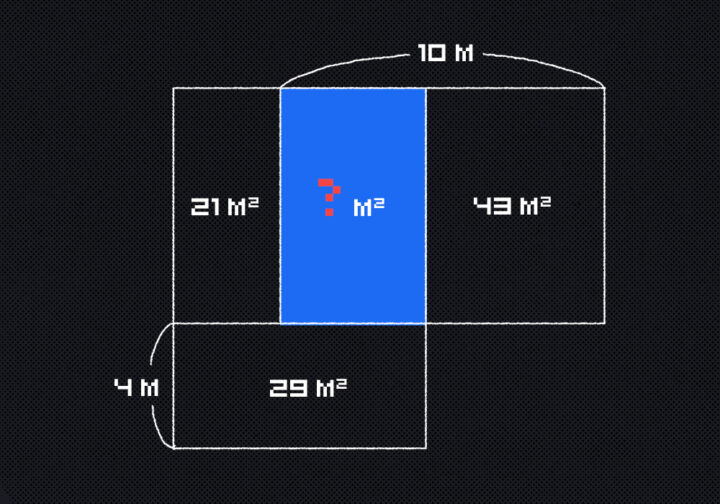
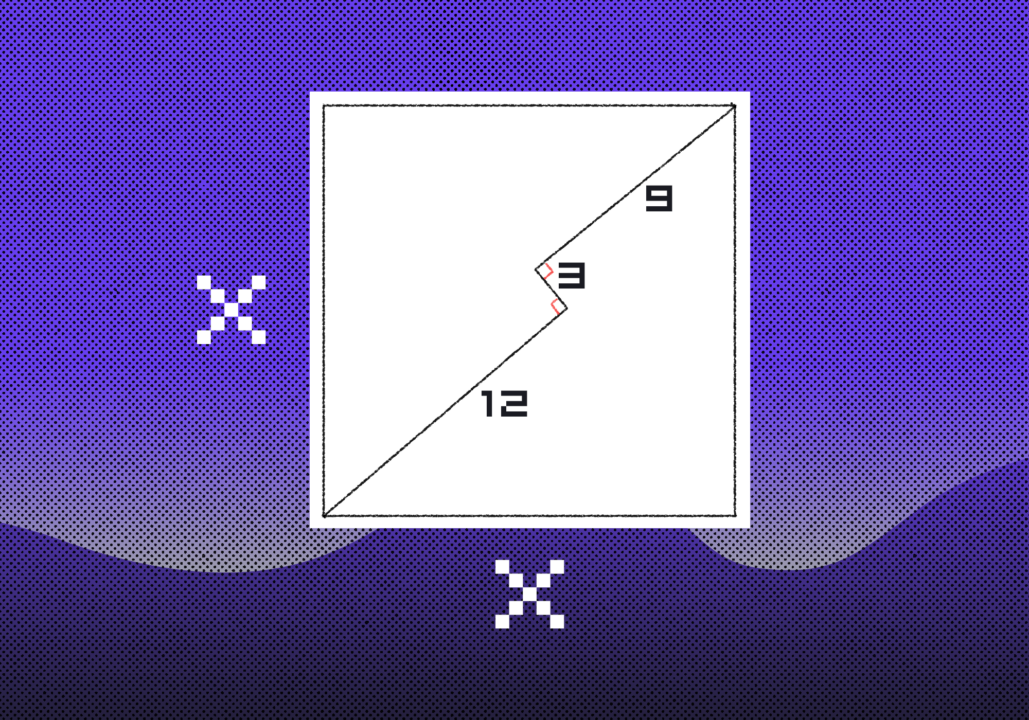
Программист решил постелить ламинат у себя дома. Для этого он посчитал размеры и площади комнат, но, приехав в магазин, понял, что не записал площадь своего кабинета. Помогите программисту найти площадь синей комнаты:
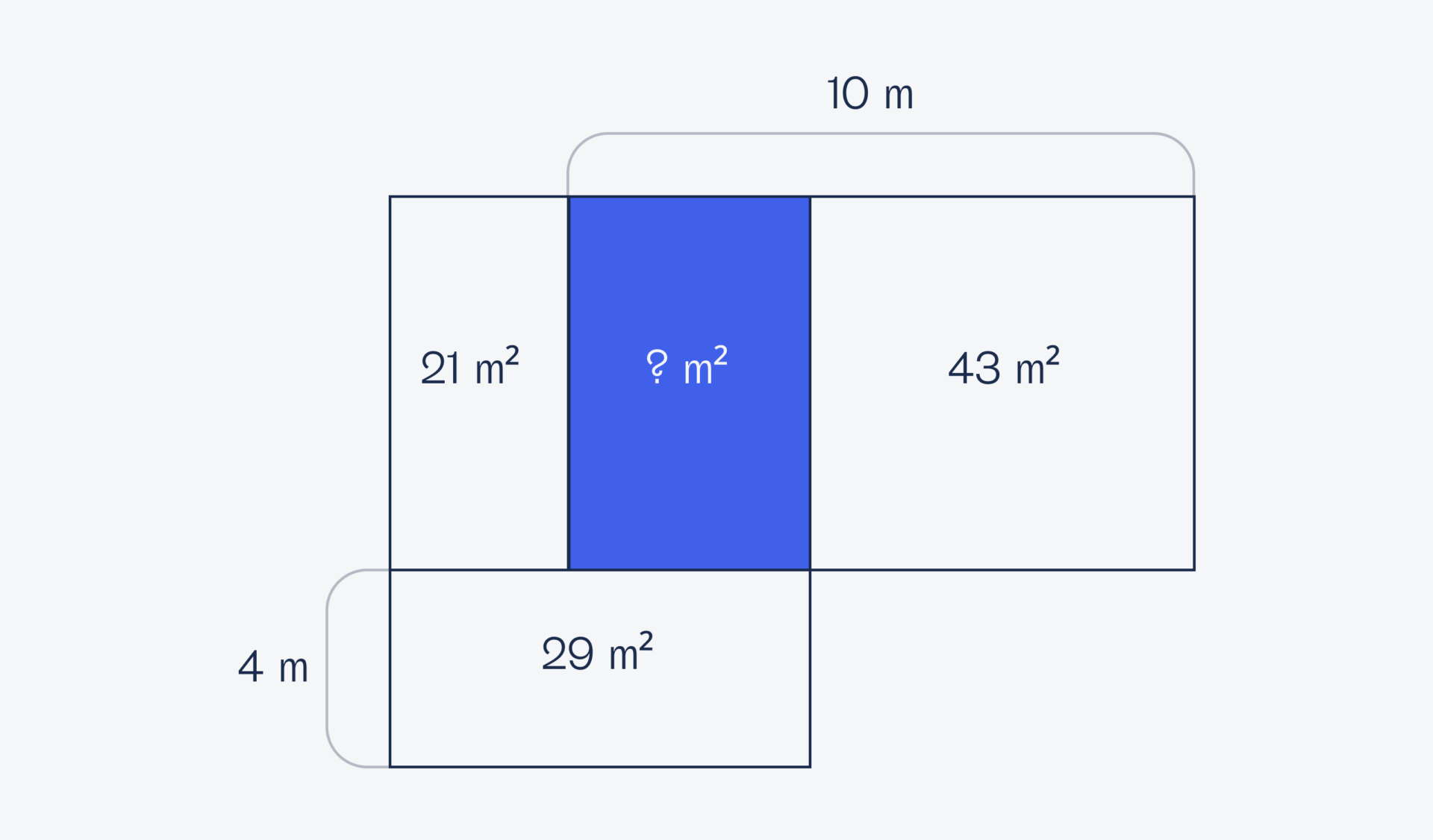
Обозначим ширину синей комнаты за X, а высоту за Y, а площадь, соответственно, будет XY:
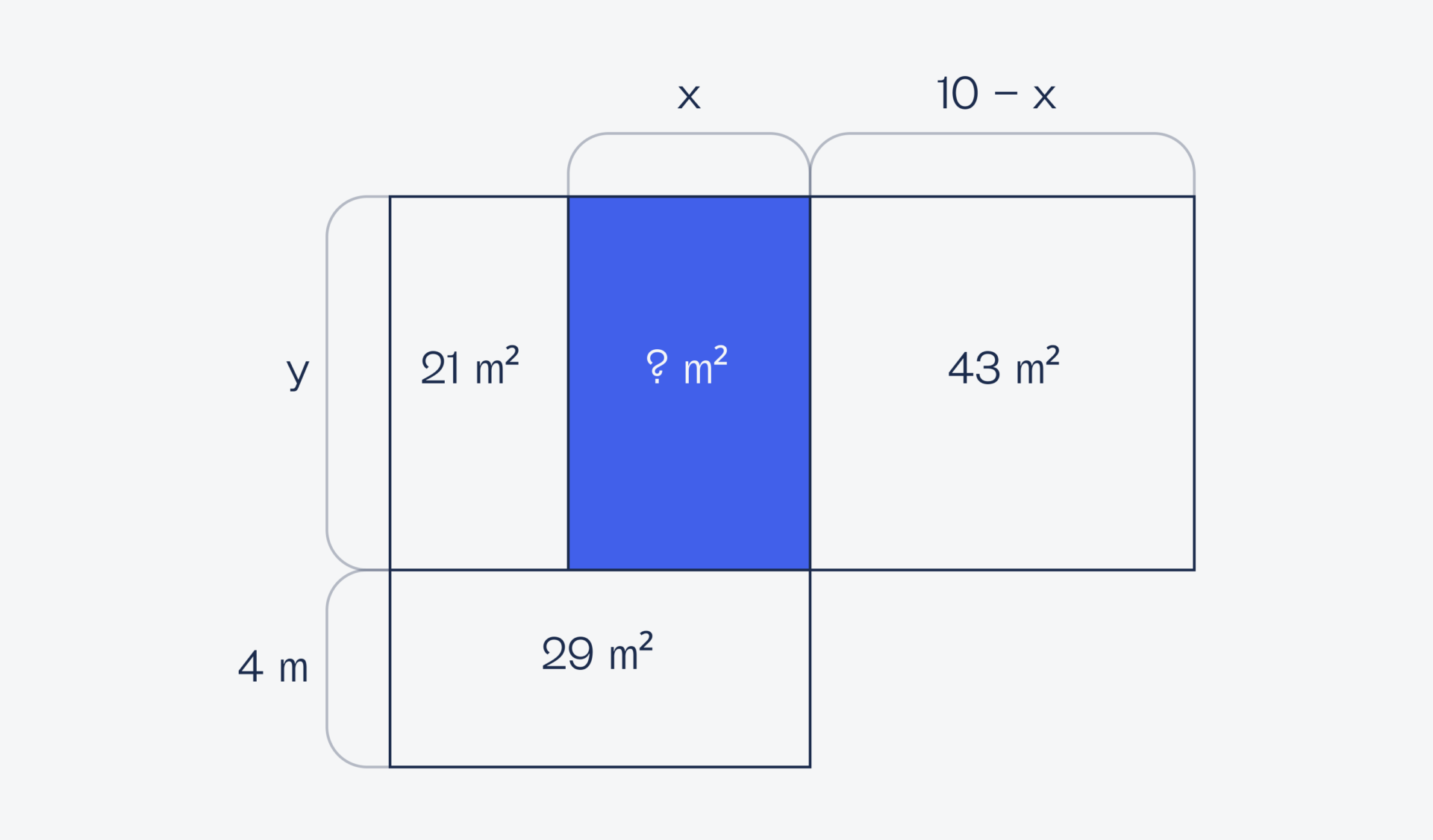
Это значит, что ширина комнаты справа будет 10 − X, а площадь — (10 − X) × Y:
(10 − X) × Y = 43
10Y − XY = 43
Теперь посмотрим на нижнюю комнату: мы знаем её площадь и высоту, поэтому можем найти её ширину: 29 / 4 = 7,25 метра.
Получается, что ширина комнаты слева равна 7,25 − X:
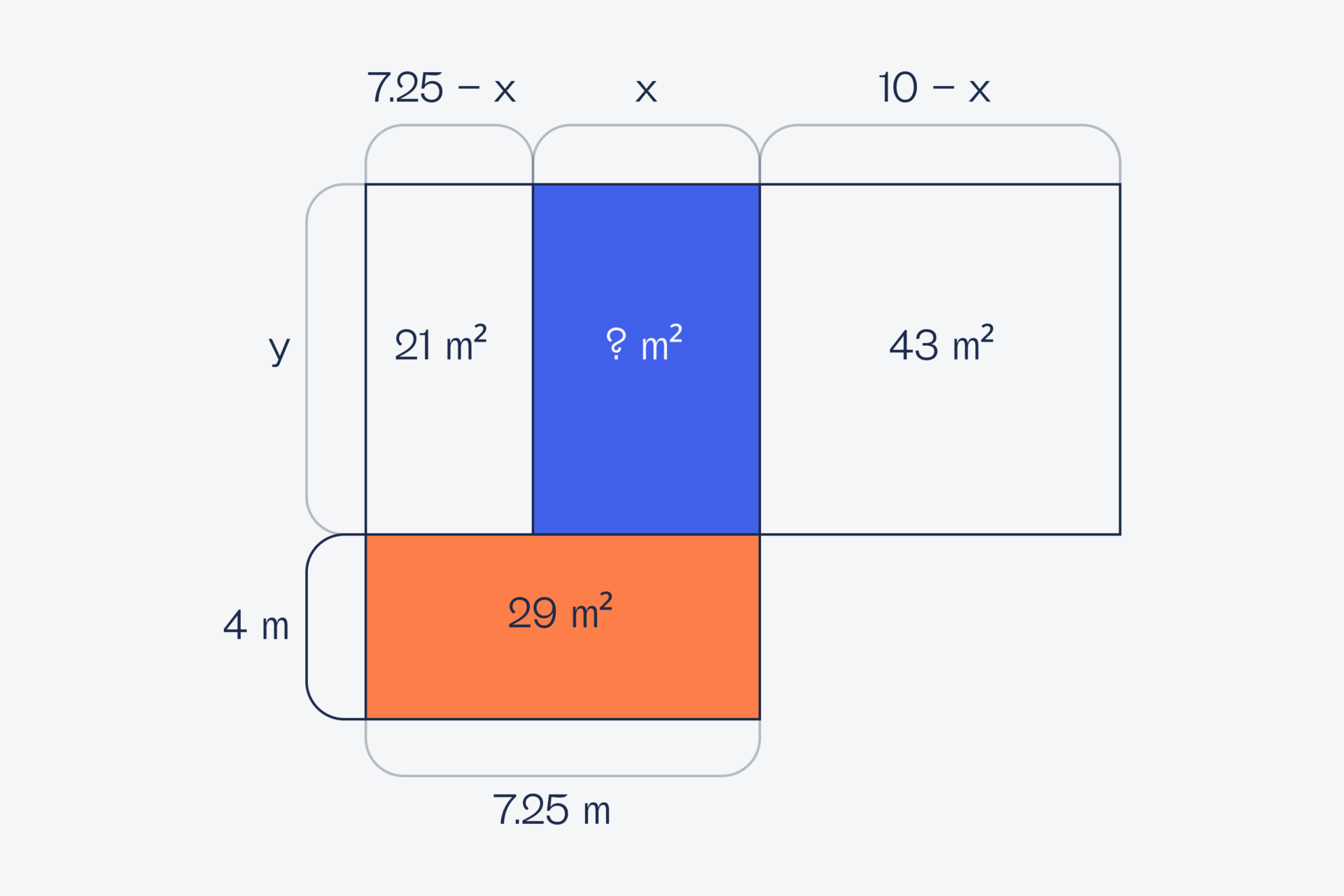
Но раз мы знаем площадь левой комнаты и её размеры, то можем легко составить такое выражение:
(7,25 − X) × Y = 21
7,25Y − XY = 21
Теперь вычтем это из первого выражения, которое мы получили для правой комнаты (10Y − XY = 43):
10Y − XY − (7,25Y − XY) = 43 − 21
2,75Y = 22
Y = 8
Подставим восьмёрку в первое выражение, которое отвечает за площадь правой комнаты:
10Y − XY = 43
80 − XY = 43
XY = 37
Но XY — это как раз площадь средней комнаты! Поздравляем, вы нашли решение.
Мысленно передвинем левую комнату вправо:
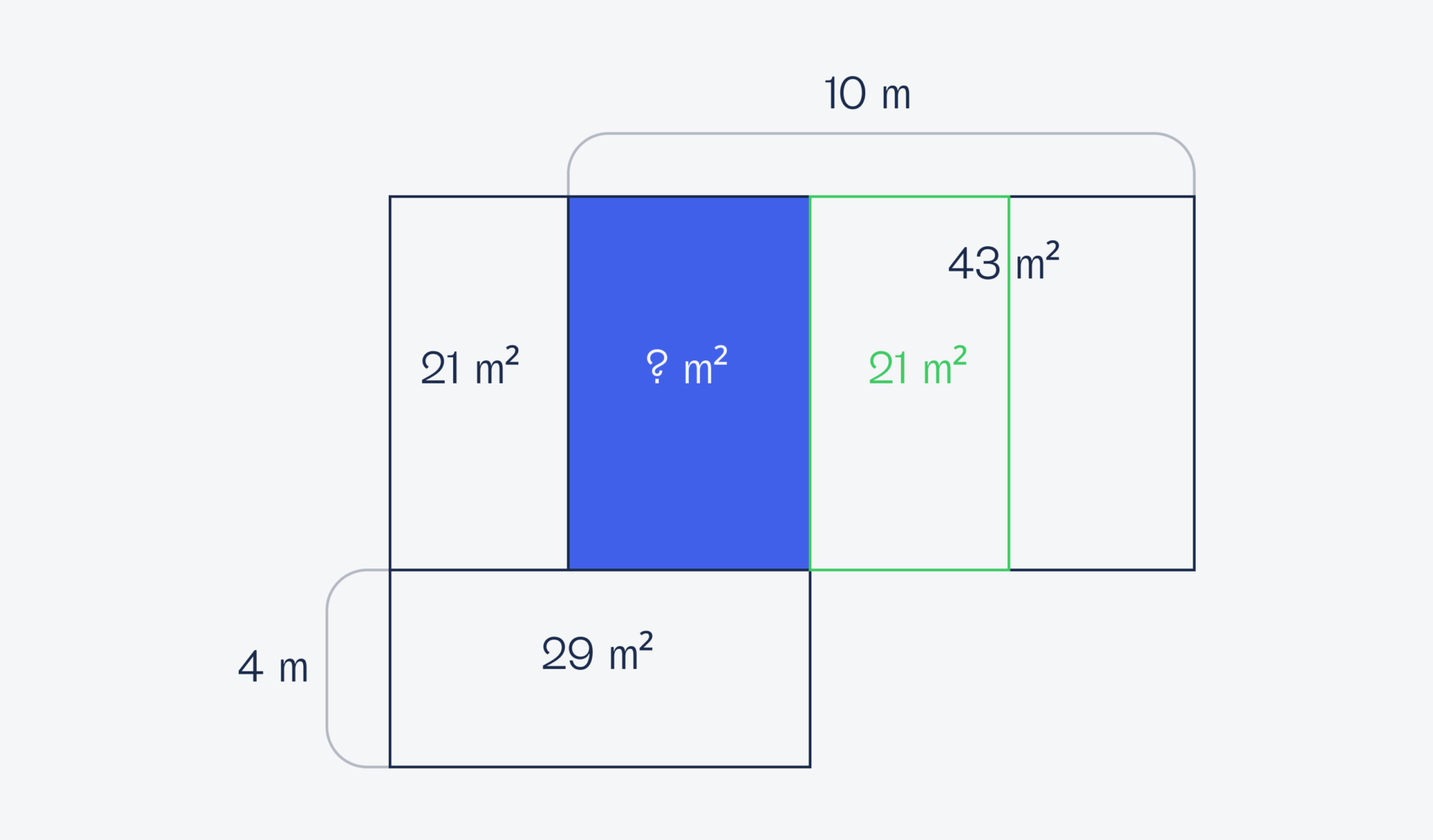
Так как площадь правой комнаты 43 квадратных метра, а левой — 21 квадратный метр, то можно найти площадь оставшегося прямоугольника: 43 − 21 = 22 м².
Теперь так же мысленно уберём нижнюю комнату и сосредоточимся на новом прямоугольнике, с той же высотой 4 метра:
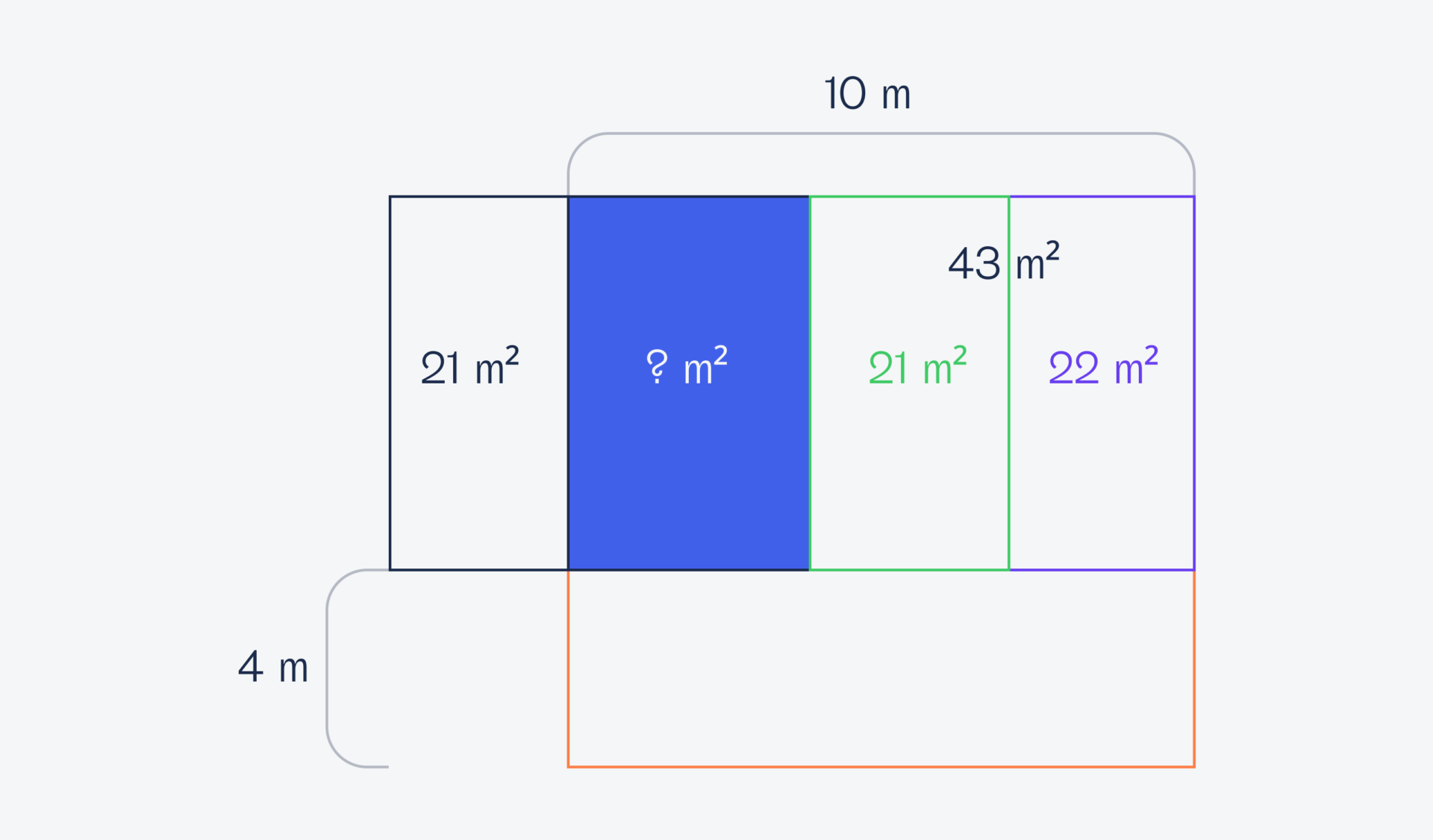
Раз мы знаем высоту (4 метра) и ширину (10 метров), то можем найти площадь этого прямоугольника: 4 × 10 = 40 м².
Теперь виртуально подвинем нижнюю комнату правее — так как слева и справа площадь прямоугольников по 21 м², то она расположится ровно по границе новой виртуальной комнаты. Точно так же найдём площадь узкого прямоугольника справа: 40 − 29 = 11 м².
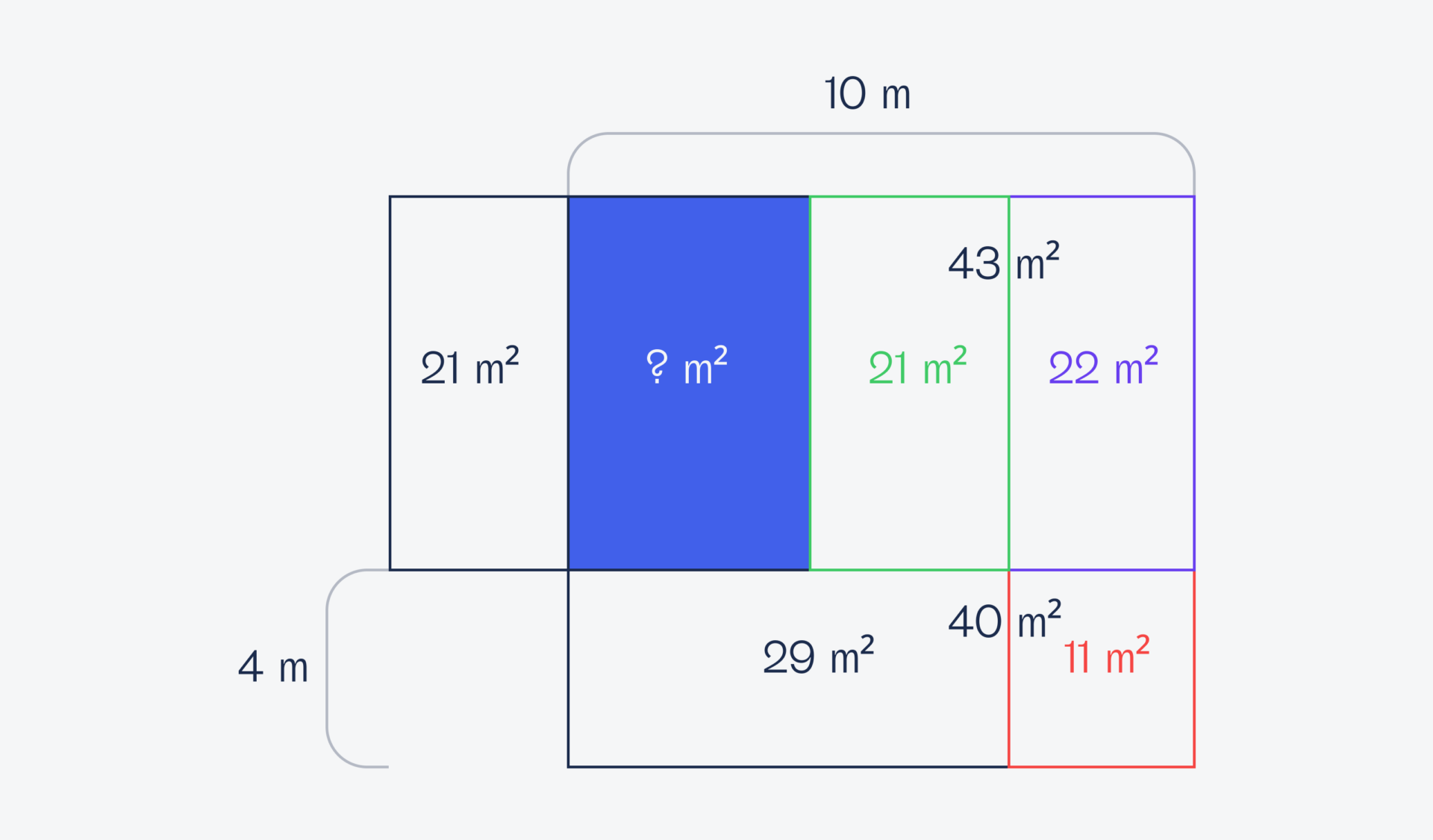
Площадь нижнего прямоугольника в два раза меньше верхнего, при этом у них одинаковая ширина. Это значит, что высота верхнего прямоугольника ровно в два раза больше высоты нижнего. Теперь вернём нижнюю комнату на место и получим, что площадь верхних двух комнат в два раза больше площади нижней и равна 29 × 2 = 58 м²:
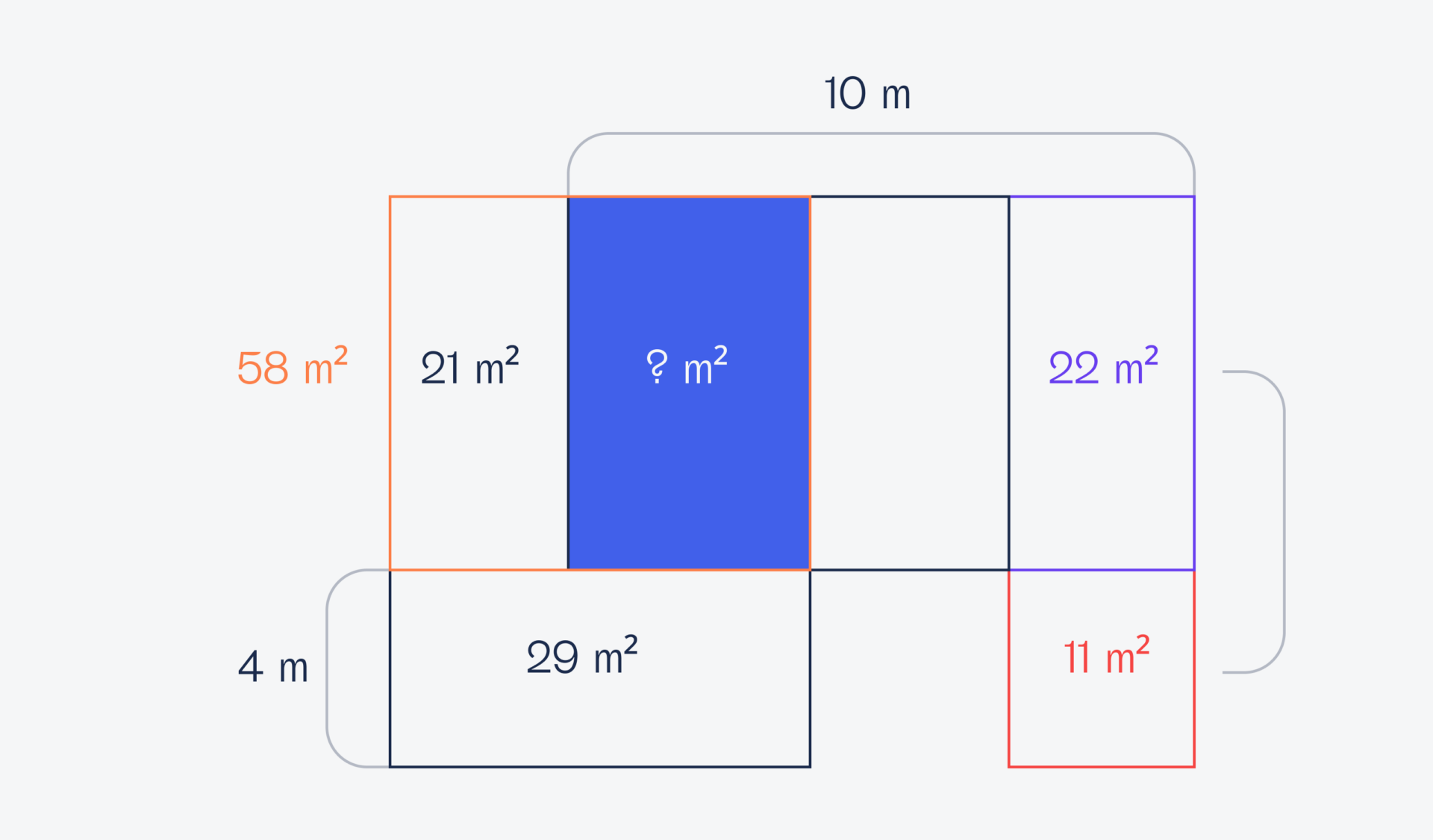
Но мы знаем площадь левой комнаты и через неё получим площадь кабинета: 58 − 21 = 37 м².