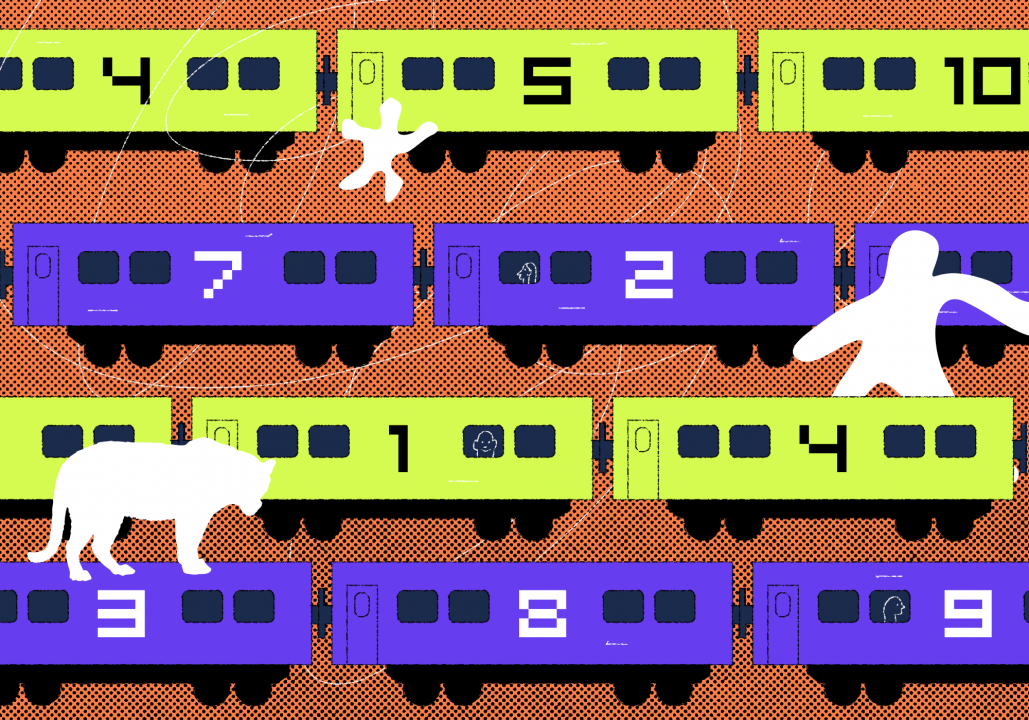Чтобы поддержать внутренний туризм, команда программистов купила билеты на поезд по Золотому кольцу и заняла все места. Всего в поезде было 11 вагонов и 381 место.
В разных вагонах ввиду конструкционных особенностей разное количество мест и, соответственно, разное количество пассажиров. Но в каждых любых трёх вагонах подряд в сумме едет ровно 99 человек. Какие бы три вагона подряд ни взяли — всё равно 99.
Сколько человек едет в девятом вагоне?
Пронумеруем вагоны и обозначим каждый вагон своей переменной. Когда мы их сложим, то получим 381:
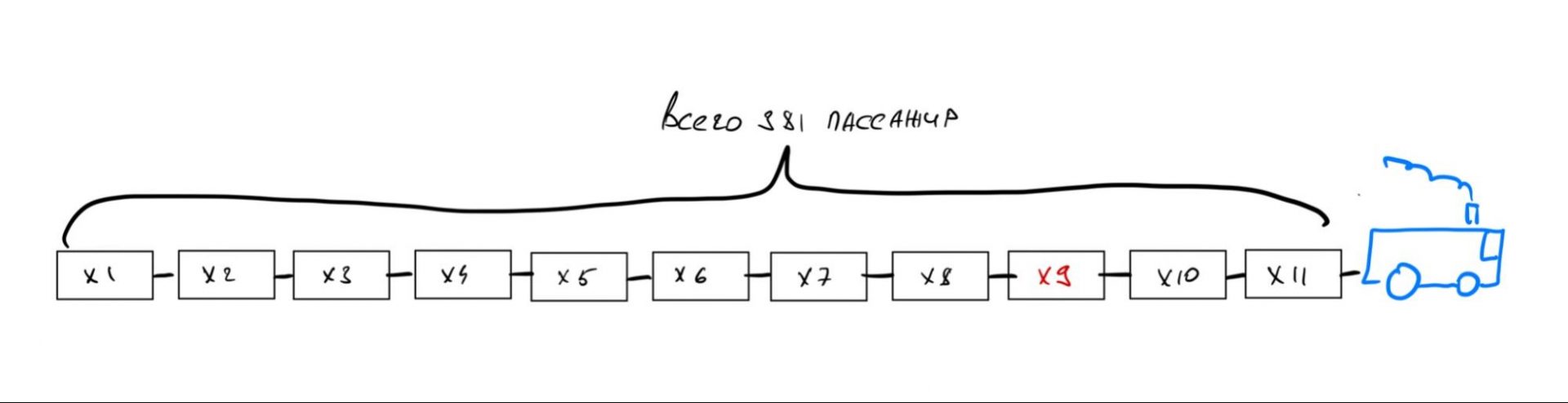
x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10 + x11 = 381
По условию три любых вагона подряд дают в сумме 99. Это значит, что:
x1 + x2 + x3 = 99
x4 + x5 + x6 = 99
x7 + x8 + x9 = 99
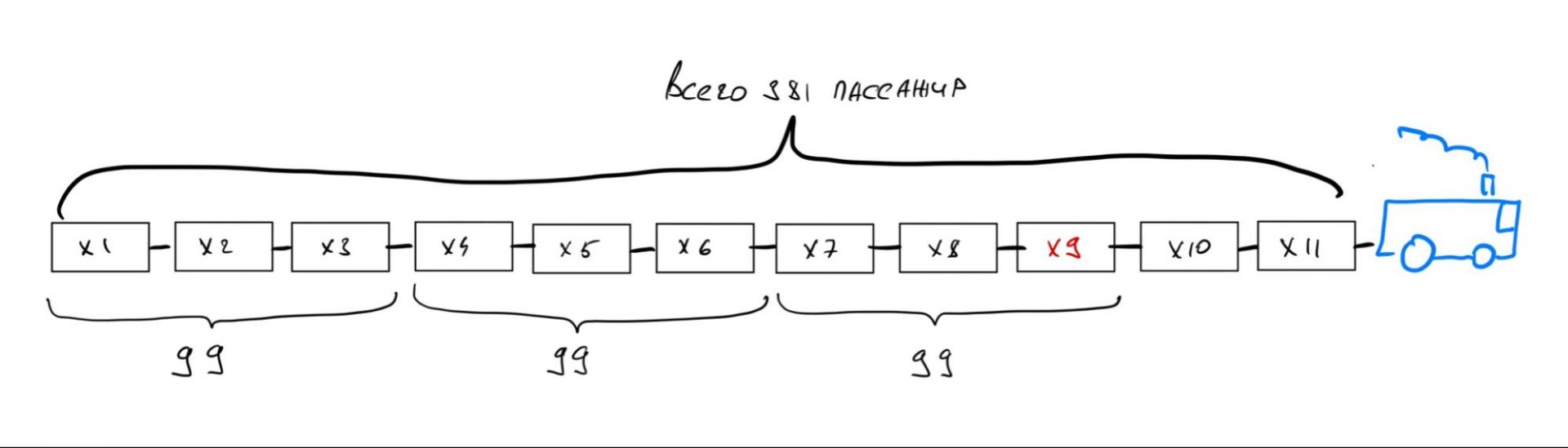
Заменим эти переменные на числа:
(x1 + x2 + x3) + (x4 + x5 + x6) + (x7 + x8 + x9) + x10 + x11 = 381
99 + 99 + 99 + x10 + x11 = 381
297 + x10 + x11 = 381
x10 + x11 = 84
С другой стороны, по условию в трёх последних вагонах тоже едет в сумме 99 пассажиров:
x9 + x10 + x11 = 99
Вычтем отсюда предыдущее уравнение:
(x9 + x10 + x11) − (x10 + x11) = 99 − 84
x9 + x10 − x10 + x11 −x11 = 15
x9 = 15
Получается, что в девятом вагоне едет 15 человек. Кстати, в третьем вагоне тоже 15 человек, потому что он девятый с конца.