Эта задача — одна из тех, которая на первый взгляд кажется неразрешимой. Но с помощью нудной логики и бесконечного итерирования можно найти решение.
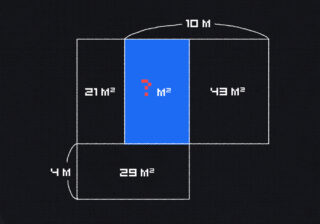
Задача такая: есть прямоугольник, заполненный квадратами разного размера. Всё, что мы знаем, — площадь самого маленького чёрного квадрата, которая равна 16 см². Нужно найти площадь всего большого прямоугольника.
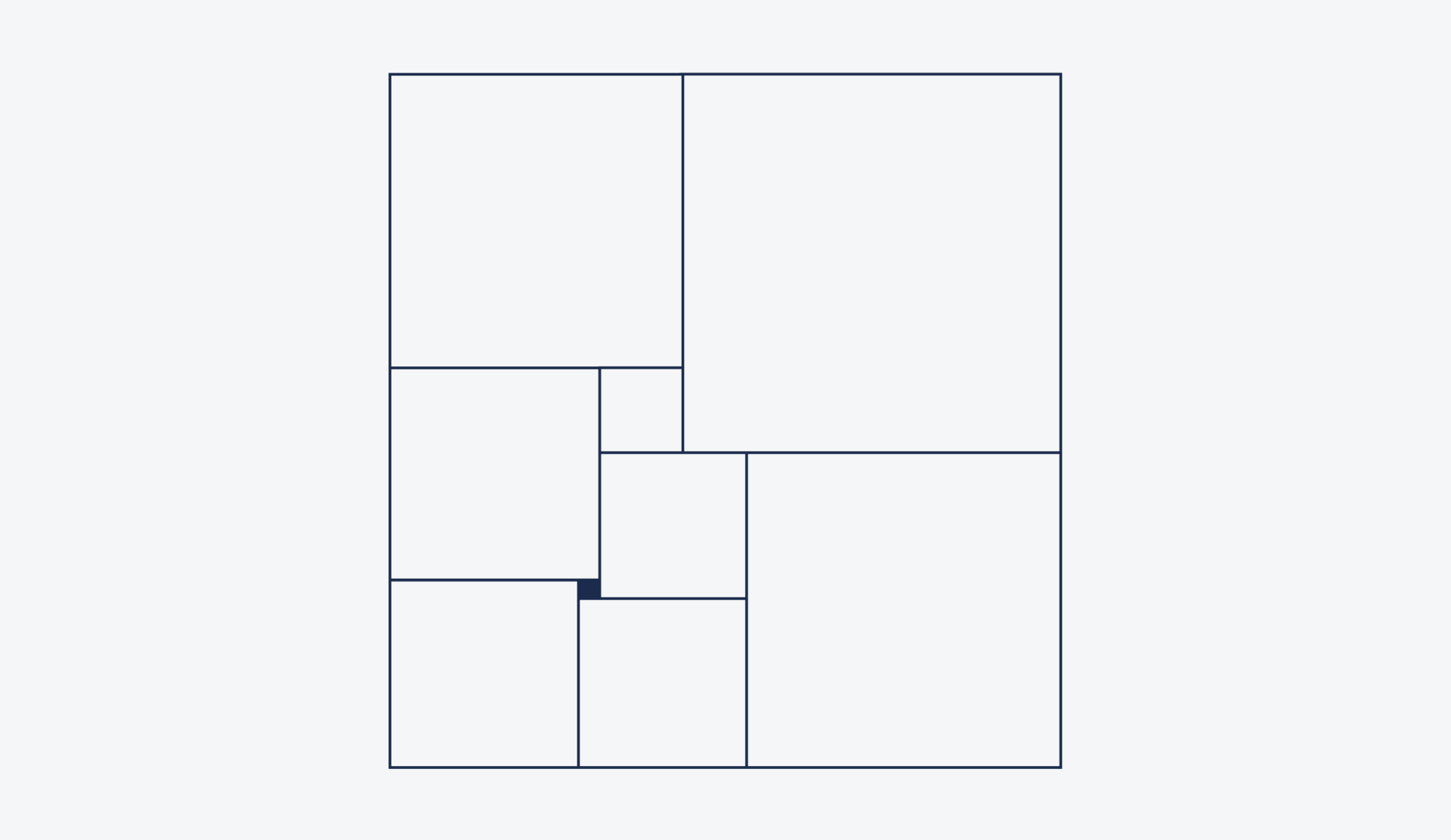
Для удобства пронумеруем все квадраты от меньшего к большему:
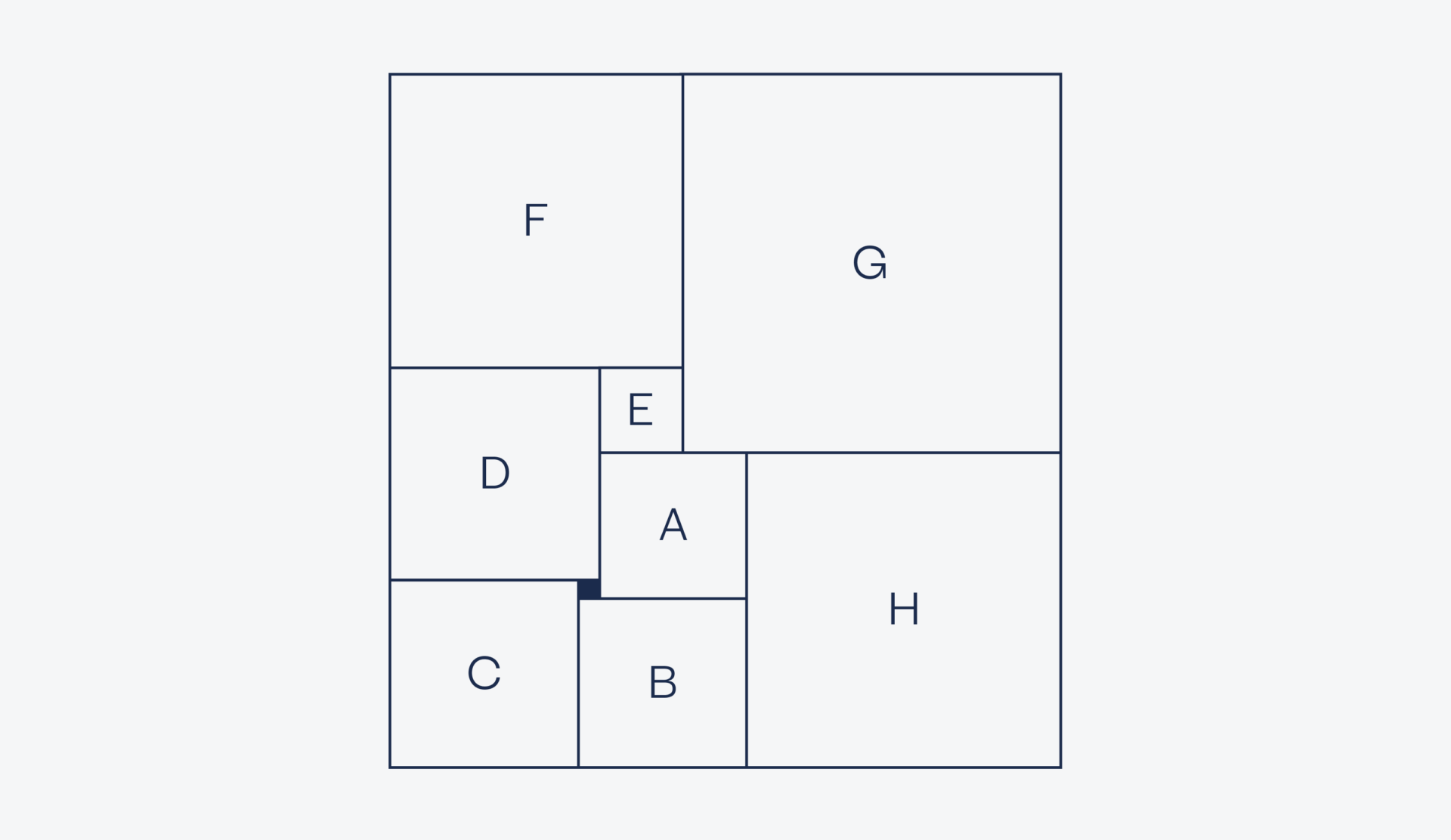
Теперь, тоже для удобства, составим таблицу с длинами сторон каждого квадрата — обозначим их маленькими буквами. Это значит, что у квадрата A будет сторона длиной a, у квадрата B — сторона длиной b и так далее.
Квадраты A — E
Раз площадь чёрного квадрата равна 16, то его сторона равна четырём — это единственное, что мы пока знаем. Теперь внимательно посмотрим на квадраты A и B: длины их сторон различаются как раз на длину стороны чёрного квадрата, то есть на 4. Получается, что:
b = a + 4
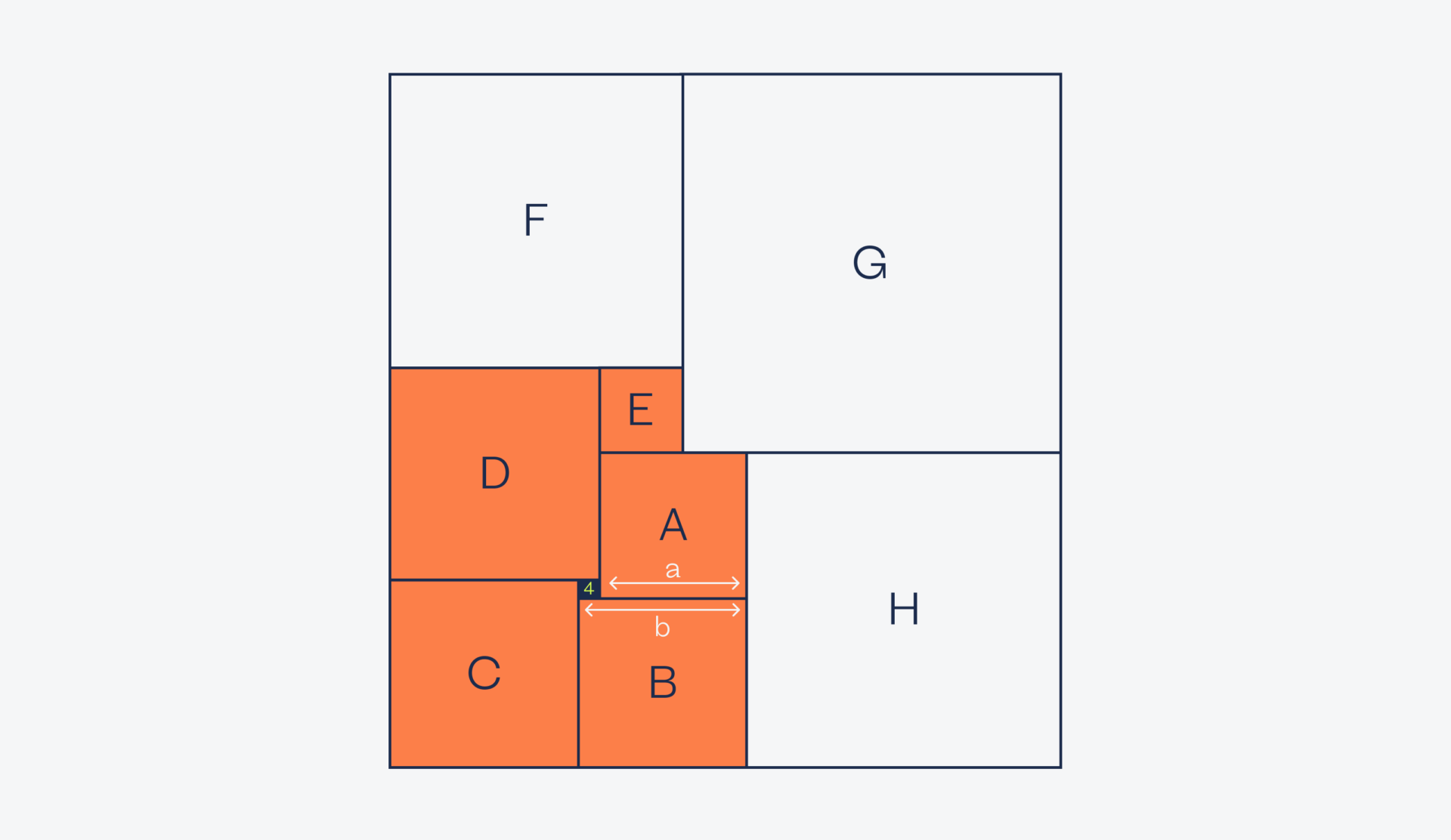
Точно так же сделаем с квадратами B и C — их длина стороны тоже различается на длину стороны чёрного квадрата, то есть тоже на 4:
c = b + 4,
но так как b = a + 4,
то c = a + 4 + 4
Следовательно, c = a + 8
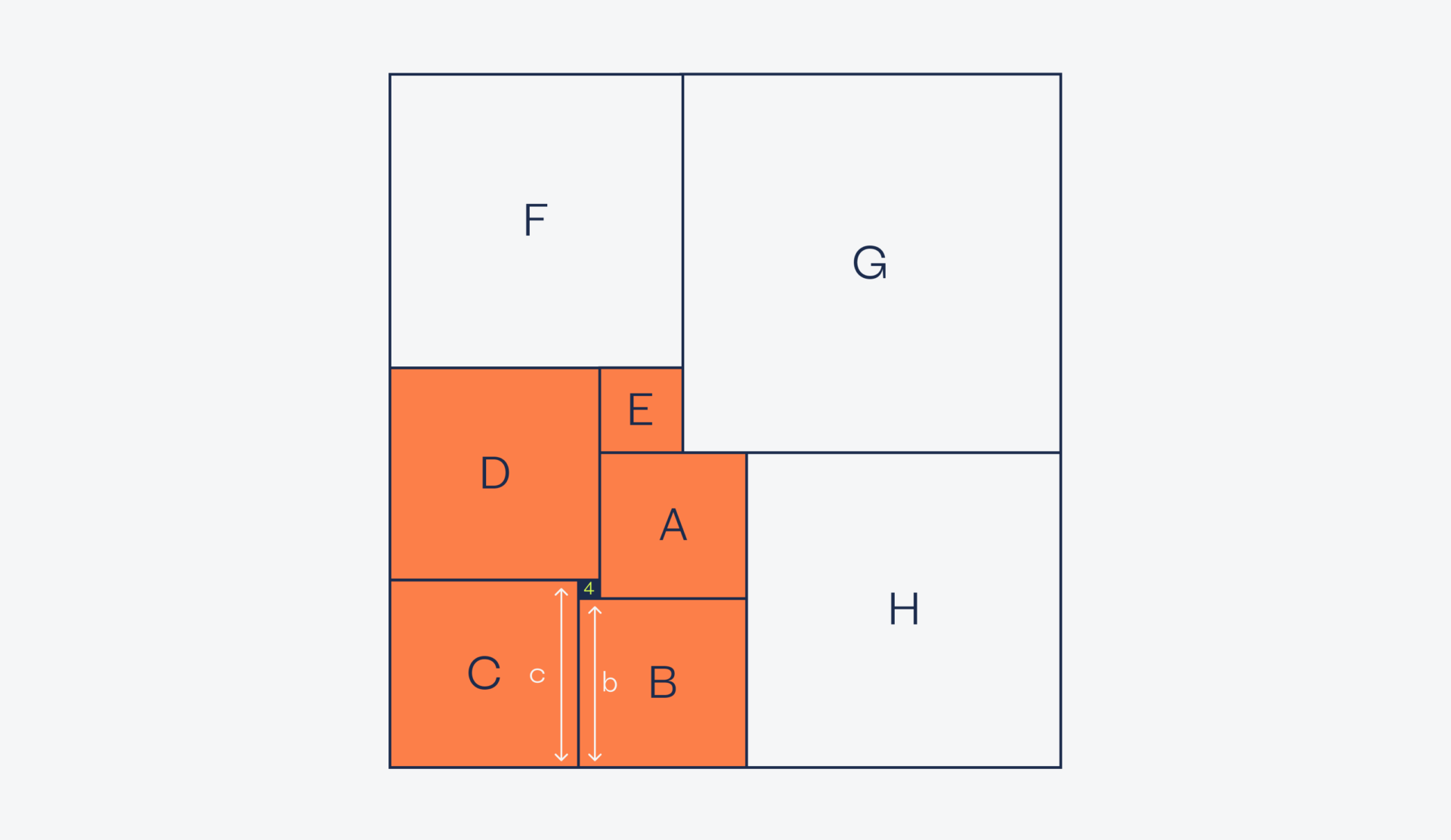
И с квадратами C и D — они тоже различаются на длину стороны чёрного квадрата:
d = c + 4,
но с = a + 8
Следовательно, d = a + 12
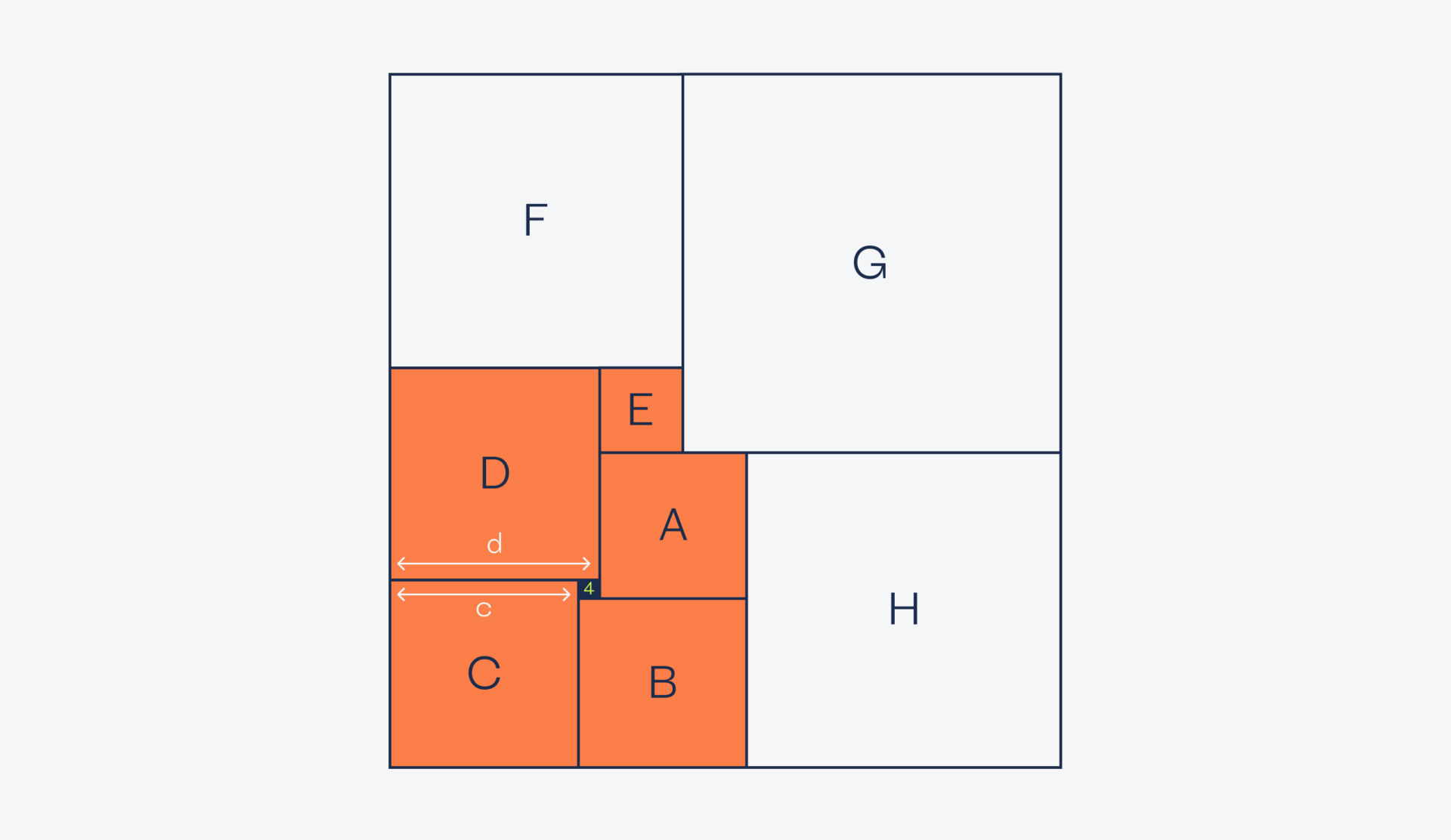
Простые подходы закончились, переходим к более сложным. Для этого посмотрим на квадраты D, A и E:
d + 4 = a + e ← подставим сюда значение d = a + 12 и посмотрим, что получится
a + 12 + 4 = a + e
a + 16 = a + e
Получается, что e = 16
Это значит, что мы нашли первую реальную длину стороны одного из квадратов, не привязанную к другим переменным. Двигаемся дальше.
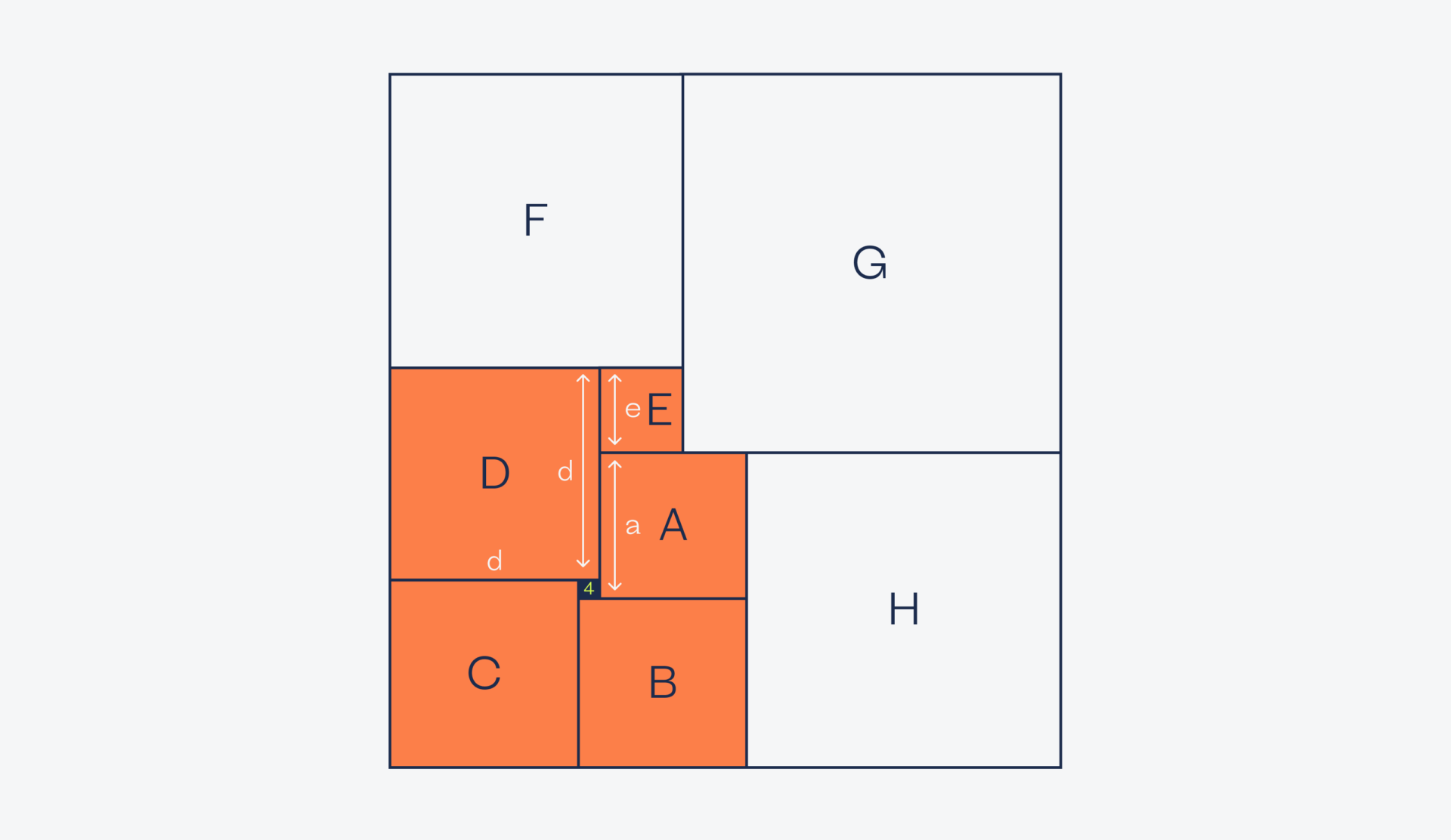
Квадраты F — H
Зная длину стороны квадрата E и размер квадрата D, посмотрим на длину стороны квадрата F:
f = d + e ← но d = a + 12, а e = 16
f = a + 12 + 16
f = a + 28
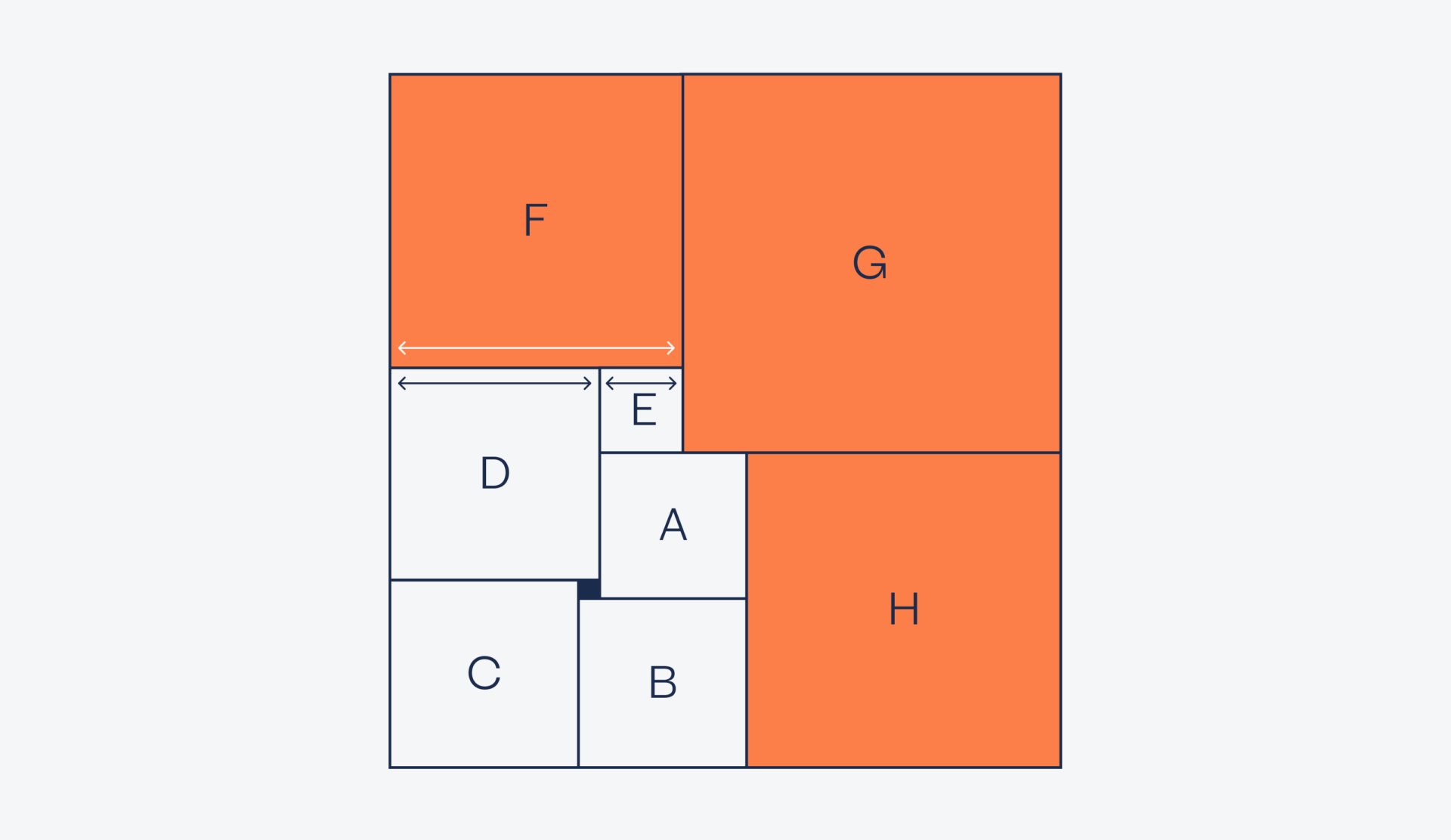
Таким же образом посчитаем длину стороны квадрата G:
g = f + e
g = a + 28 + 16
g = a + 44
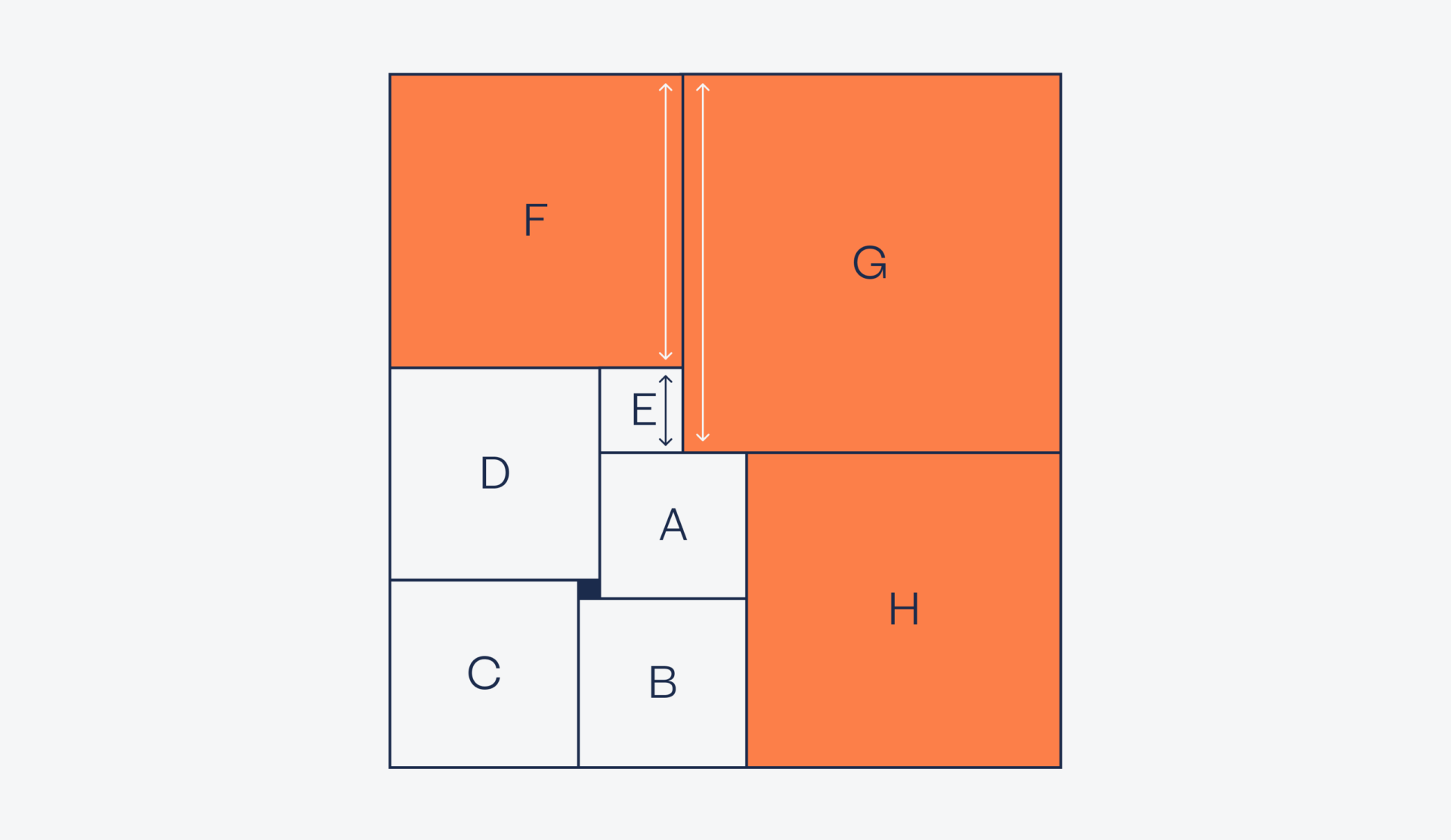
И наконец, посчитаем длину стороны квадрата H через длины сторон квадратов A и B:
h = a + b
h = a + a + 4
h = 2a + 4
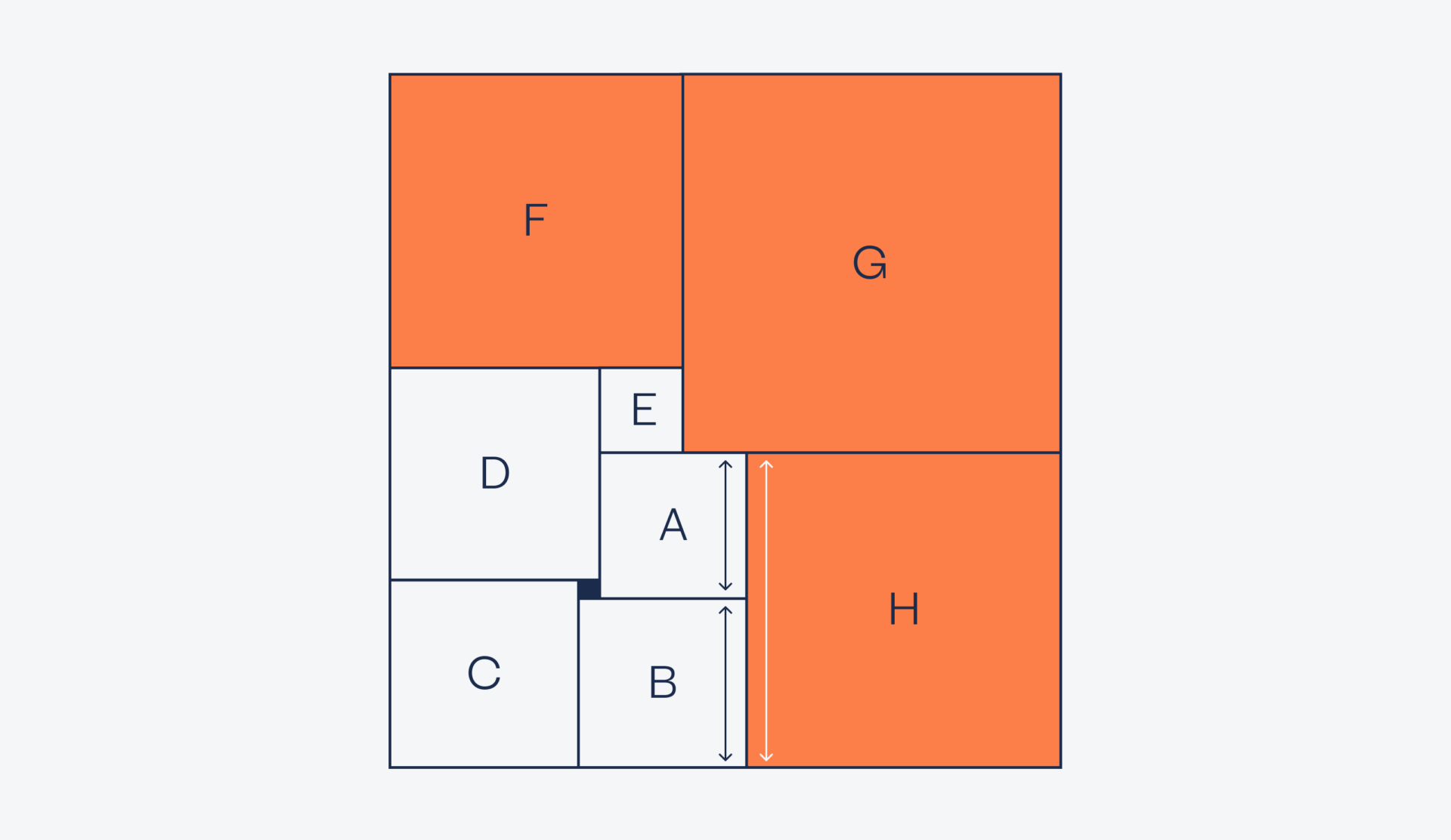
Находим значения длин сторон H и A
Мы знаем длину стороны каждого квадрата, если выразить их через длину стороны квадрата A, но для общей площади нам нужны точные значения. Чтобы их найти, посмотрим на квадраты E, G, A и H.
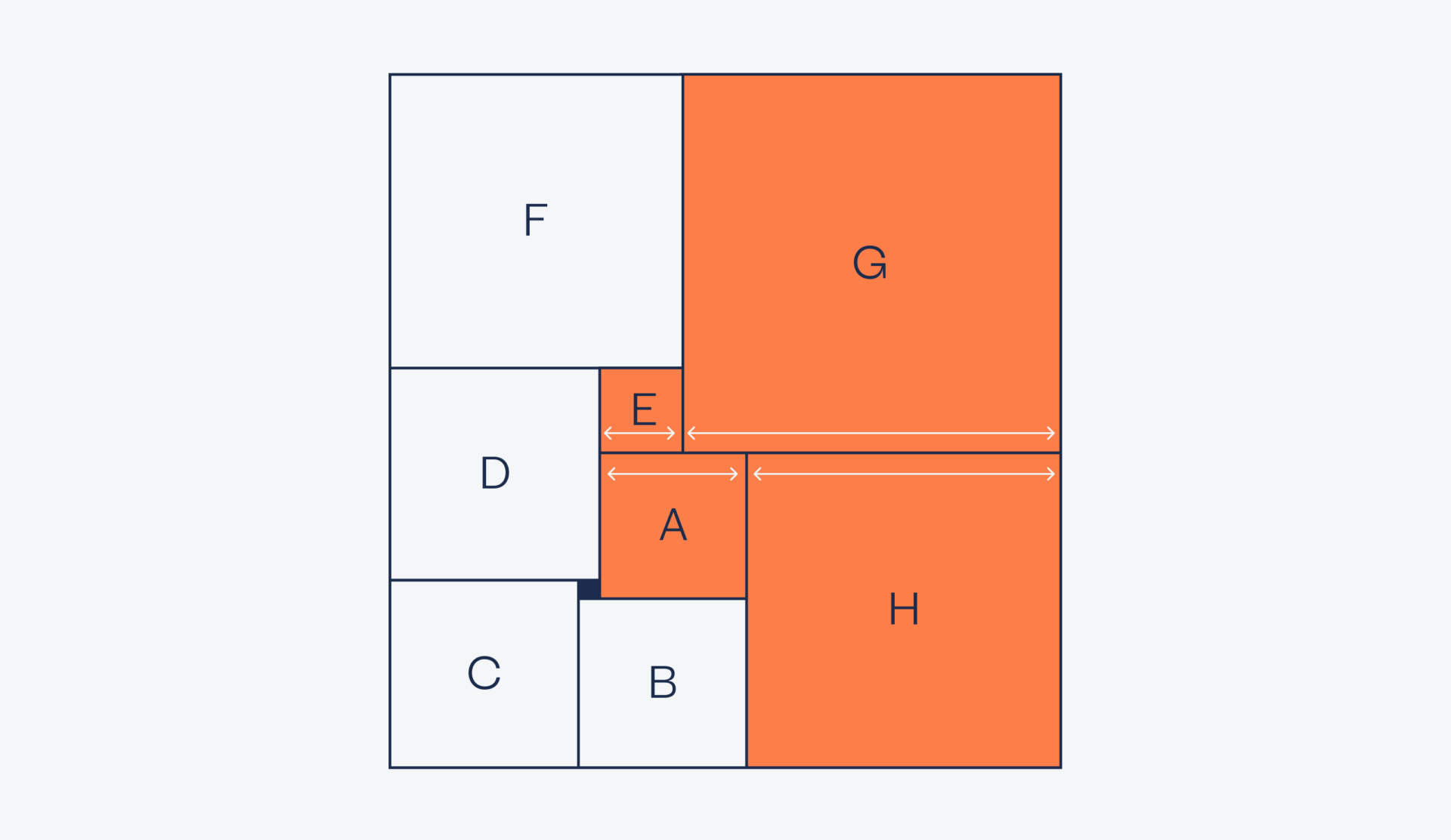
Видно, что сумма длин сторон квадратов E и G равна сумме длин сторон квадратов A и H:
e + g = a + h
16 + a + 44 = a + h
16 + 44 = h + a − a
h = 60
Раз мы знаем, чему равно h, то можем из h = 2a + 4 найти a:
h = 2a + 4
60 = 2a + 4
2a = 56
a = 28
Находим общую площадь прямоугольника
Чтобы найти площадь основного прямоугольника, нужно перемножить длины его сторон. Длина верхней стороны равна f + g, а боковой — g + h:
S = (f + g) × (g + h)
S = (a + 28 + a + 44) × (a + 44 + 60)
S = (2a + 72) × (a + 104)
S = (56 + 72) × (28 + 104)
S = 128 × 132 = 16 896
Это и есть ответ — площадь прямоугольника с квадратами равна 16 896 см².