Сегодня задачка на логику и геометрию, как в школе. Это не нужно в ИТ, но иногда нужно отвлекаться.
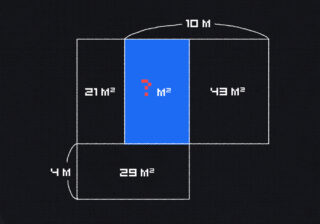
Вот картинка, тут всё понятно. Нужно найти площадь треугольника:
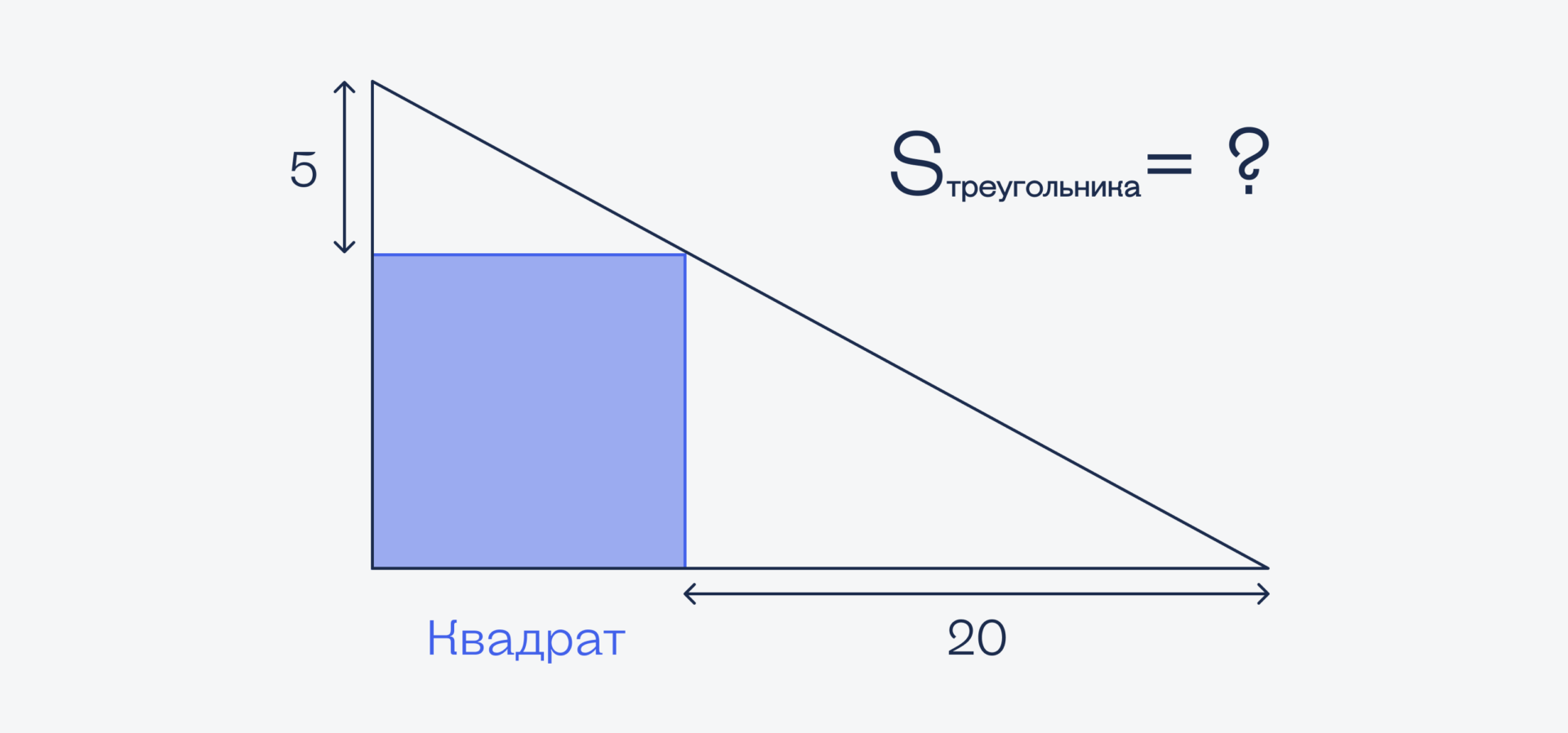
Решение с тригонометрией
Так как у нас в треугольник вписан квадрат, это значит, что обе его стороны находятся под прямым углом к основанию треугольника:
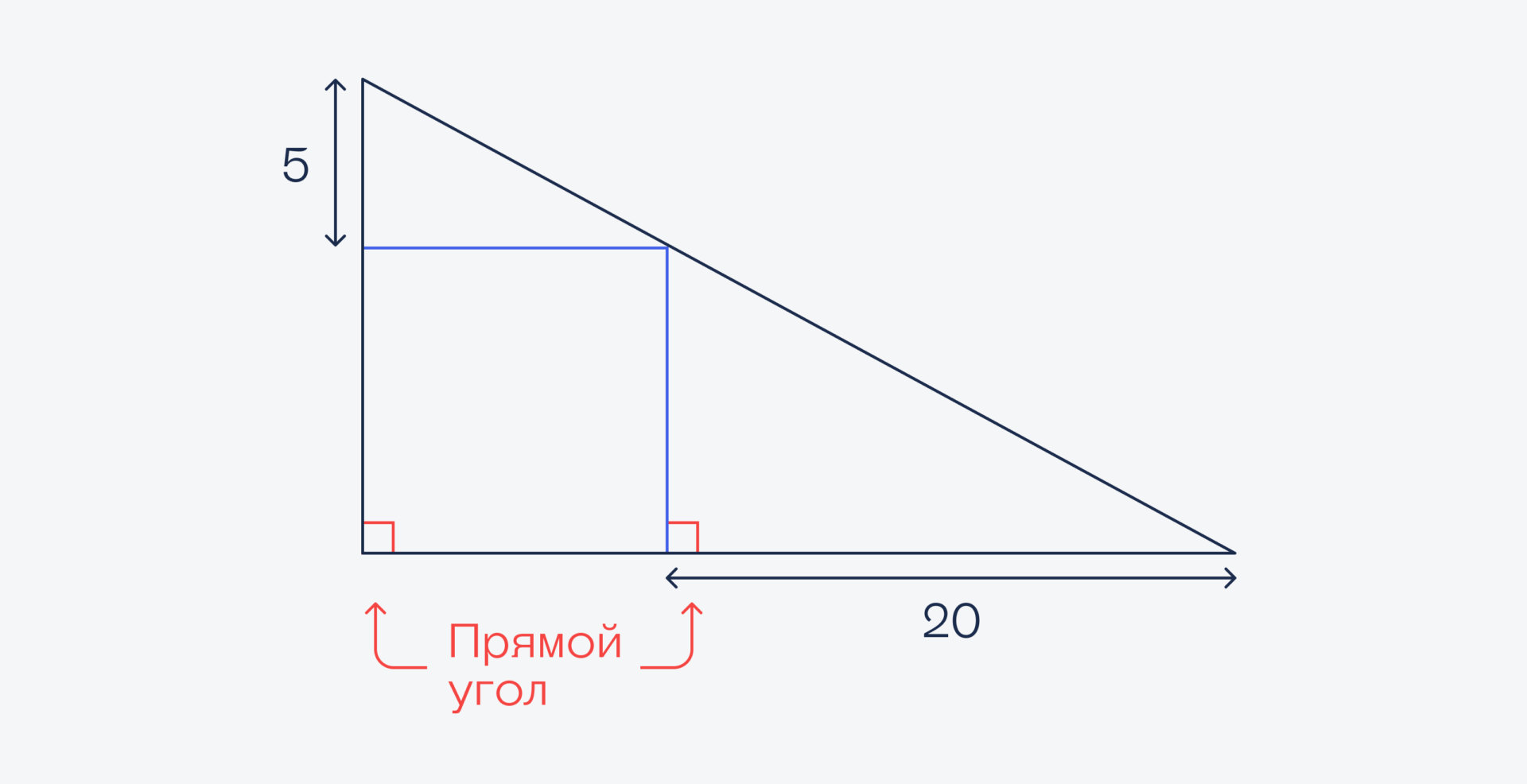
А раз так, то угол, который образуется при пересечении наклонной линии, совпадает с углом наклона этой линии к основанию:
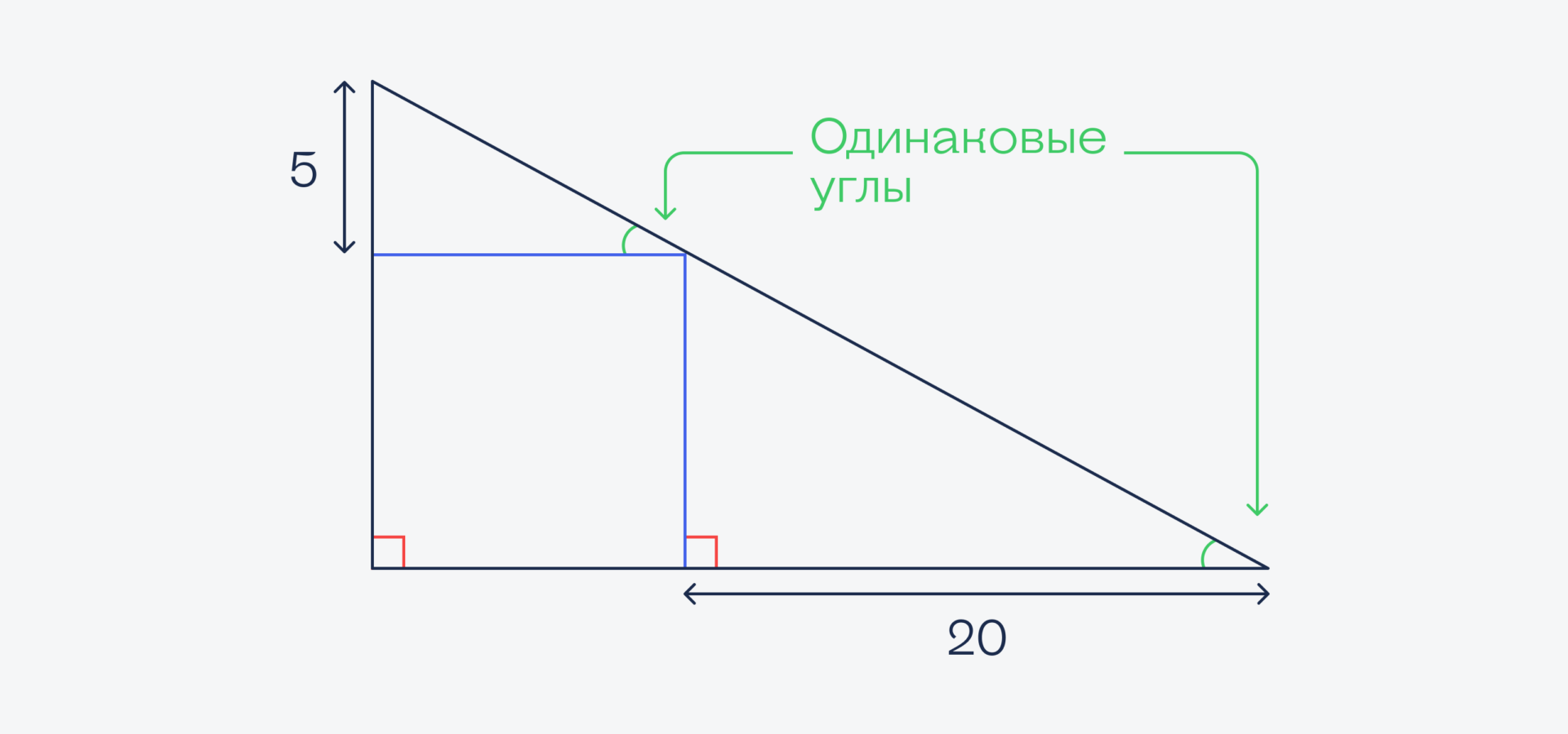
Если у треугольников есть два одинаковых угла, то такие треугольники называются подобными. А раз они подобные, то и соотношение сторон у них будет одно и то же. Обозначим сторону квадрата за X:
Теперь построим соотношение:
5 / X = X / 20 ← решим это уравнение
X² = 5 × 20 = 100
X = 10
Зная сторону квадрата, можно легко найти площадь всего треугольника:
(5 + 10) × (10 + 20) / 2 = 15 × 30 / 2 = 225
Нестандартное решение без тригонометрии
Представим, что мы ничего не знаем про тригонометрию, углы и подобие треугольников. Возьмём наш рисунок и мысленно достроим его до прямоугольника:
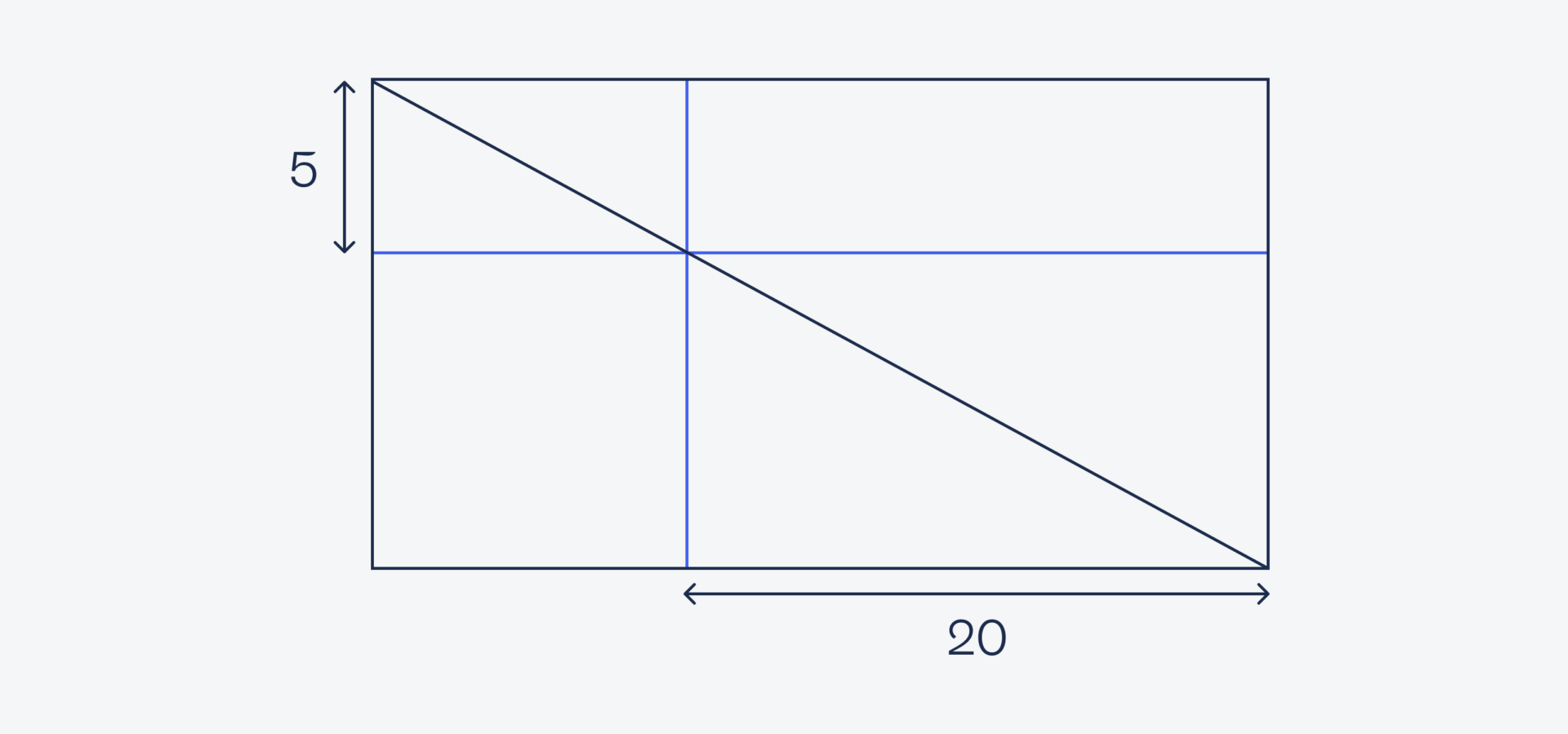
Так как у квадрата все углы прямые, то и синие линии у нас тоже пересекаются под прямыми углами между собой и с внешним прямоугольником. Это значит, что мы можем перенести известные размеры на оранжевый прямоугольник:
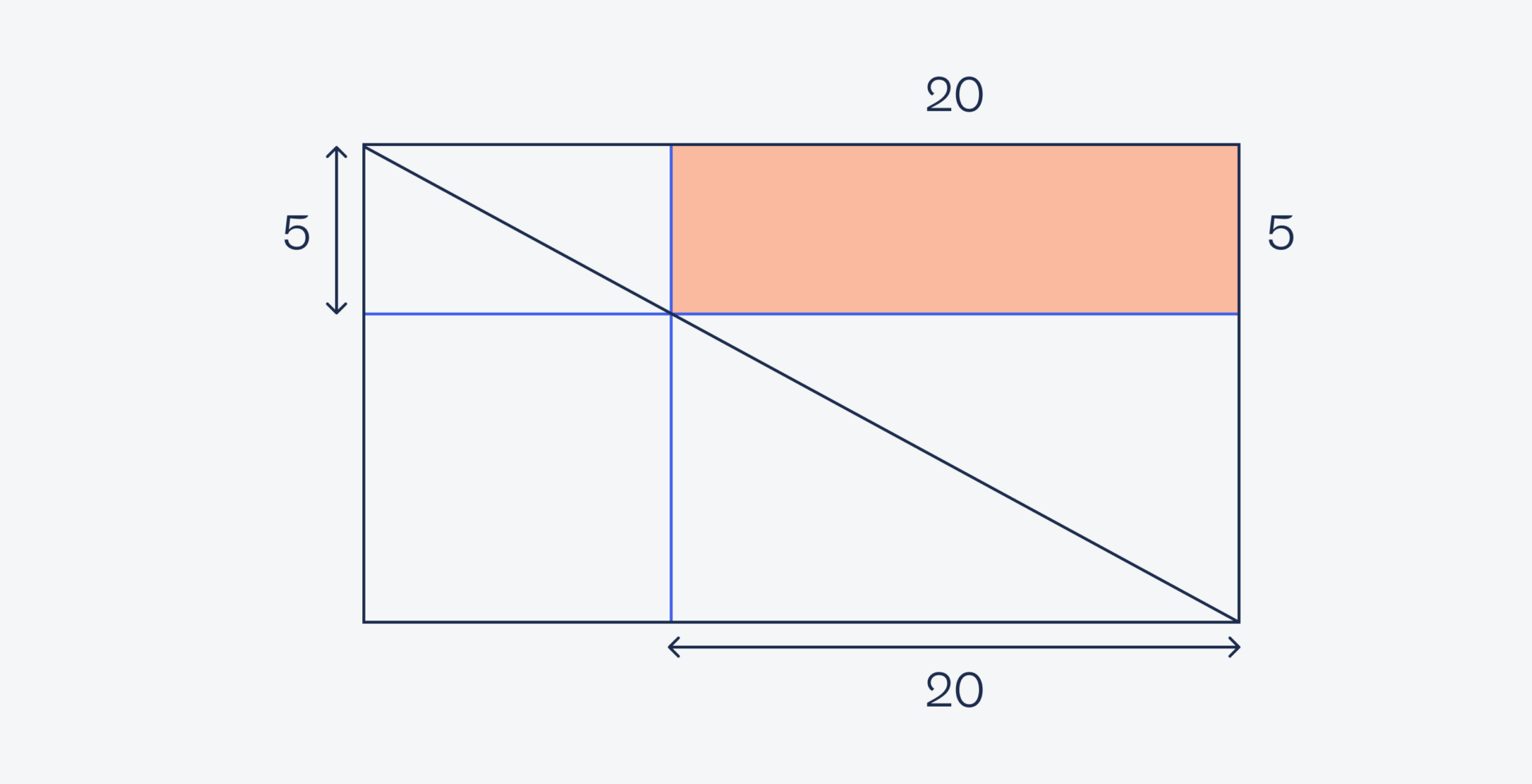
Зная длину и ширину, посчитаем его площадь — 5 × 20 = 100.
Теперь посмотрим на рисунок так: у нас есть прямоугольник, разделённый пополам по диагонали. Это значит, что площадь нижних треугольников совпадает с площадью верхних треугольников:
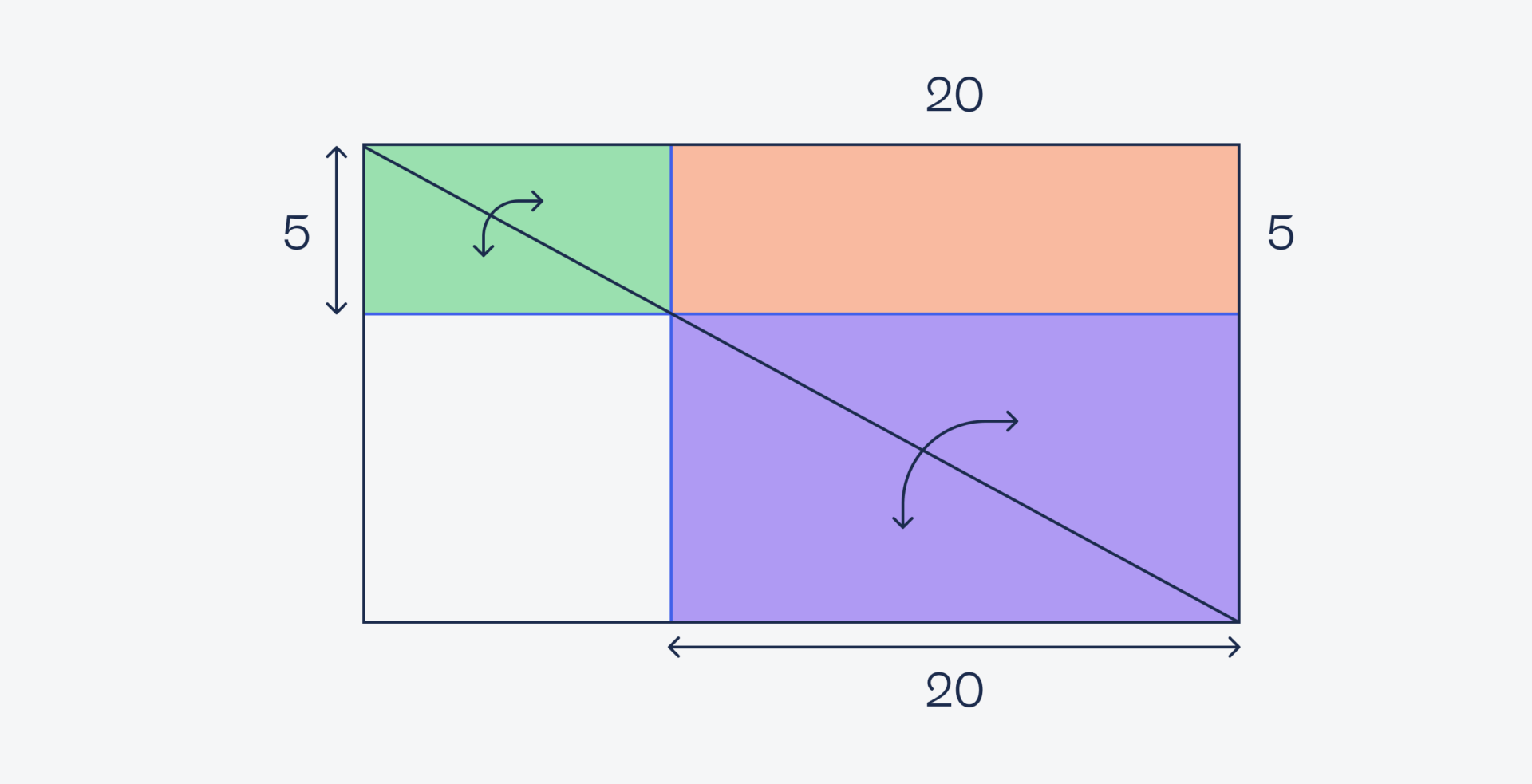
Но раз у нас часть площадей в верхнем и нижнем треугольнике одинаковая, их можно вычесть из обеих частей:
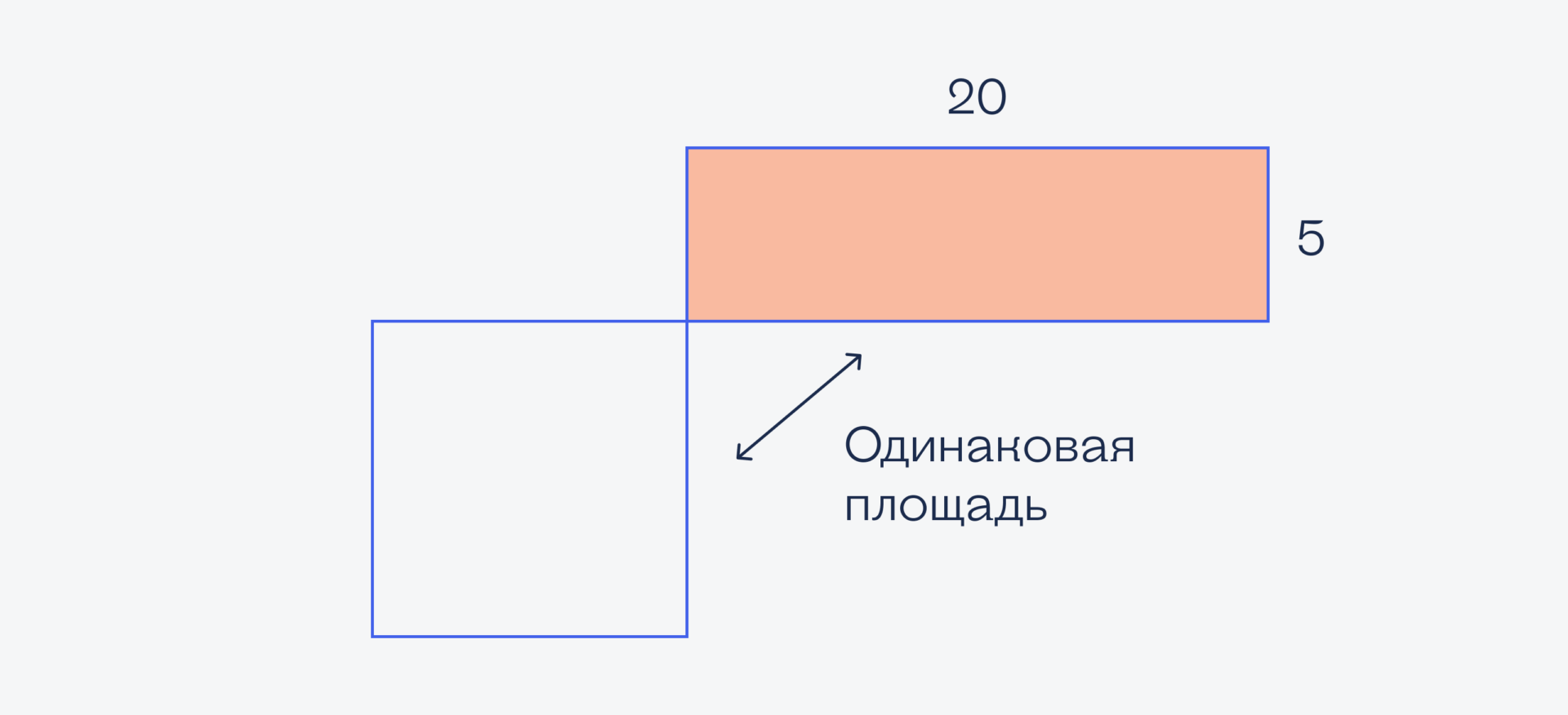
Получается, что площадь оранжевого прямоугольника совпадает с площадью квадрата. А мы знаем, что площадь прямоугольника равна 100; получается, чтобы найти сторону квадрата, нужно извлечь квадратный корень:
√100 = 10
Значит, сторона квадрата равна 10. Этого достаточно, чтобы посчитать всю площадь треугольника:
(5 + 10) × (10 + 20) / 2 = 15 × 30 / 2 = 225