Продолжаем разговор про оптимизацию игр и про хитрости, на которые идут разработчики. Напомним, о чём речь:
- каждая программа запускается на каком-то железе, возможности которого всегда ограничены;
- чем быстрее программа работает на слабом железе, тем круче, потому что слабое железо дешевле и более массово используется;
- чтобы программы работали быстрее, используют разные оптимизации: трюки с памятью, процессорные хаки и нестандартные алгоритмы;
- одна из таких оптимизаций — использование магических констант. Про это и поговорим.
Исторический контекст
В девяностых уже были трёхмерные игры: Doom, Duke Nukem 3D, System Shock, Turok, Unreal, Wolfenstein, Half-Life и другие.
Трёхмерными эти игры были с разными ограничениями: например, в части из них трёхмерными были только коридоры, а враги и объекты были двумерными «спрайтами». В других была трёхмерная геометрия, но статичный свет. В третьих нельзя было посмотреть дальше условных 50 метров — геометрия уходила в «туман». Наконец, для игр с реально хорошей графикой нужны были 3D-ускорители типа 3Dfx.
Прорыв в оптимизации
В 1999 году вышла игра Quake III Arena — трёхмерная стрелялка с красивой графикой и динамическим освещением. Она оказалась на голову выше всего, что было в тот момент на рынке:
- выглядела красиво: эффекты, взрывы, красивые текстуры, прозрачности;
- имела динамическое освещение объектов: если у тебя в руках была цилиндрическая пушка и ты поворачивался в разные стороны, эта пушка освещалась по-разному;
- рисовала больше геометрии, поддерживала большие залы с большим числом противников;
- работала без тормозов даже на слабом оборудовании того времени.
В принципе, технически уже ничего не мешало делать такие игры в то время, кроме одного нюанса — быстродействия. Если бы Quake III сделала какая-нибудь другая компания, эта игра потребовала бы намного больших ресурсов. А у разработчиков ID Software как-то получилось дичайше эту игру оптимизировать.
Чтобы понять эту оптимизацию, нам нужно немного поговорить про векторы и их вычисление.

Алгоритм освещения трёхмерных моделей
Если совсем упростить, то логика у освещения такая:
- У нас есть трёхмерная модель, которая составлена из виртуальных треугольников — полигонов. Каждый полигон как-то ориентирован в пространстве.
- Есть источник света с координатами относительно нашего полигона.
- В зависимости от взаимного расположения полигонов и света каждый полигон имеет разную степень освещённости. Если полигон «смотрит» на свет, то он освещён ярче. Если полигон «отвёрнут» от света, то он освещён более тускло.
- Чтобы понять степень отвёрнутости полигона от света, из его центра проводят виртуальную перпендикулярную линию — «нормаль». Нормаль — это вектор, то есть палка с каким-то направлением. Направление выражается координатами.
- Наконец, нужно рассчитать, насколько нормаль «смотрит» на источник света. Это даст нам степень освещённости этого полигона. Останется только его покрасить в нужную степень яркости.
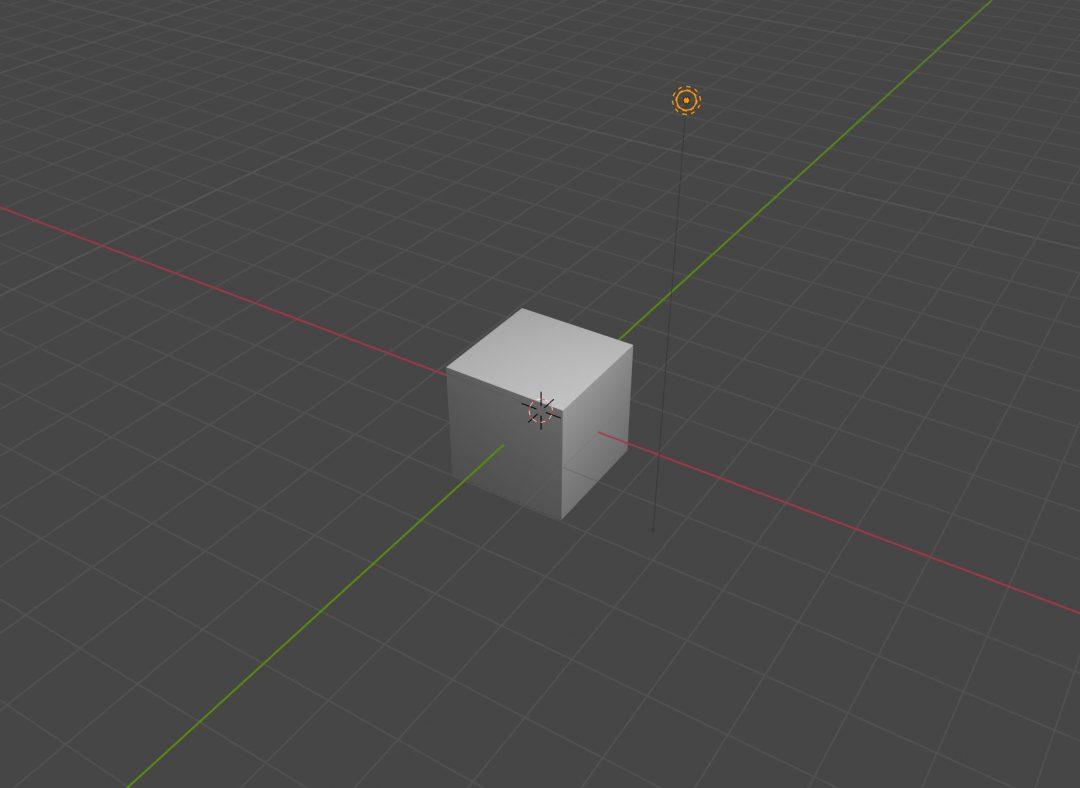
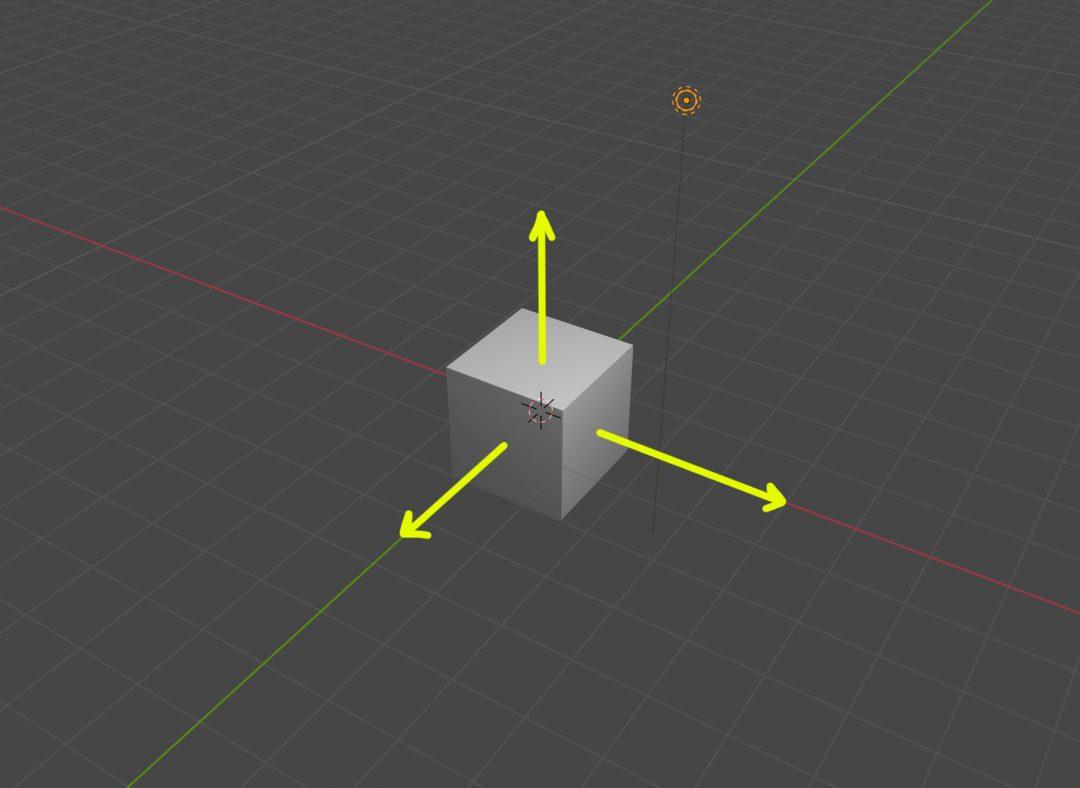
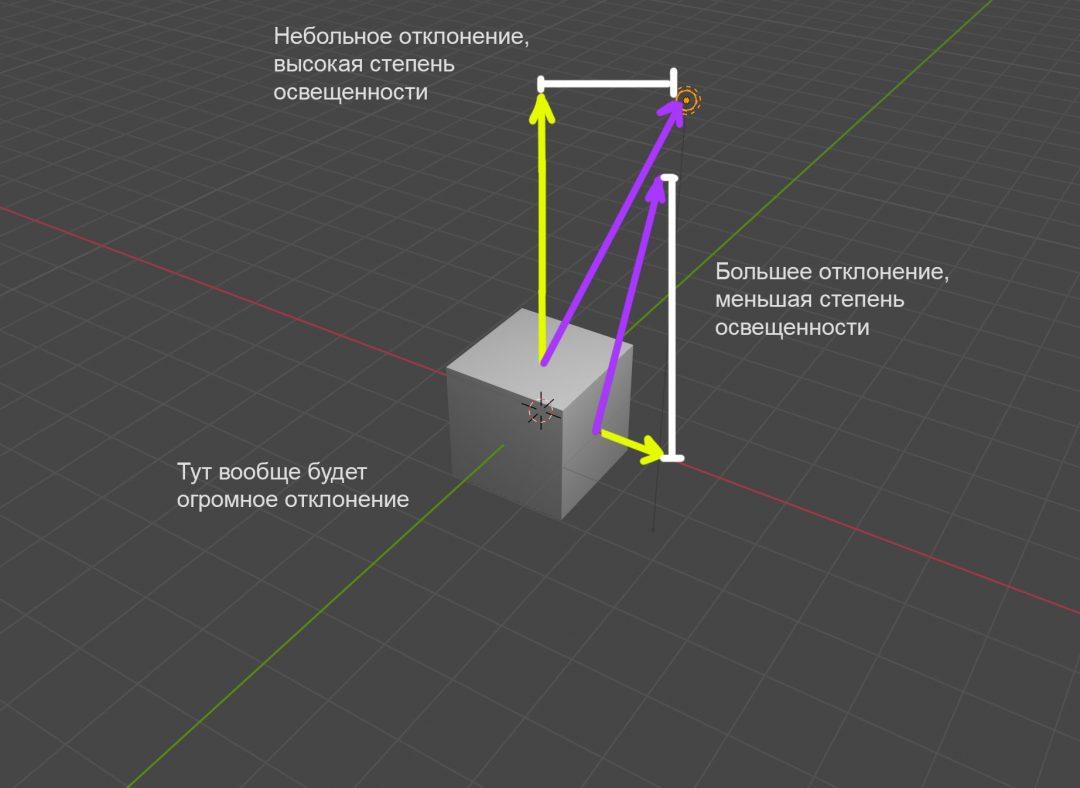
Соответственно, если вектор нормали будет очень близок к вектору источника света, то соответствующий полигон будет считаться ярко освещённым (как верхний полигон). А если между векторами нормали и света будет большая разница, этот полигон у нас будет освещён пропорционально меньше (как полигон справа).
Вот этот процесс нужно повторять для каждого полигона много раз в секунду, и у нас получится иллюзия трёхмерного изображения.
Кстати, если хотите изучить вопрос векторов, у нас есть очень подробный и довольно понятный для новичков цикл про линейную алгебру:
В чём сложность алгоритма
Считать разницу между векторами довольно легко, потому что это простые операции сложения и вычитания их координат. А вот исходный вектор посчитать довольно сложно, потому что он основывается вот на этой формуле:
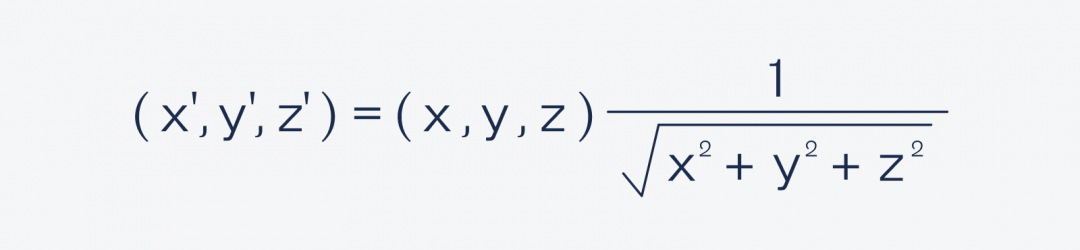
В этой формуле — ключ к оптимизации. Но сначала расскажем о том, как всё считалось до оптимизации.
Классический подход
Видно, что в этой формуле используется три математических операции:
- Возведение в квадрат.
- Сложение.
- Извлечение квадратного корня.
Самая трудоёмкая задача здесь — извлечь квадратный корень числа. На эту операцию компьютер тратит сотни тактов, а таких операций ему нужно делать очень много каждую секунду — игра же динамичная, там всё в движении, надо постоянно считать новый свет.
Именно по этой причине большинство подобных трёхмерных игр требовало мощного железа. На слабом компьютере игра просто не успевала посчитать все квадратные корни.
Трюк с волшебной константой
Разработчики Quake III Arena подсмотрели у коллег особенный трюк, который давал достаточно точный результат за одну сотую времени от исходного алгоритма. Трюк довольно сложный, но соль вот в чём:
- Вместо того чтобы честно считать квадратный корень, используются две хитрости.
- Первая — побитовый сдвиг исходных чисел. Это сложно, сейчас можно не вникать.
- Вторая — волшебная константа. Программистам удалось найти такое число, которое при последующем умножении давало почти точное значение квадратного корня.
Волшебную константу в буквальном смысле вписали в исходный код алгоритма, и получилось. Погрешность вычислений корня не превышала 0,2% — для игры этого более чем достаточно. В итоге вместо нескольких тысяч операций процессор использовал несколько десятков и получал результат нужной степени точности. Алгоритм освещения стал работать почти в сто раз быстрее в некоторых сценах, а это значит, что игру можно будет запускать даже на слабом железе.
Джон Кармак, основатель ID Software, тоже не разобрался, как работает эта магия (потому что алгоритм был где-то подсмотрен и никто не знал, как именно он работал). Своё недоумение логикой работы он выразил своим знаменитым комментарием в коде:
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
#ifndef Q3_VM
#ifdef __linux__
assert( !isnan(y) ); // bk010122 - FPE?
#endif
#endif
return y;
}Почему это важно
Сейчас подобная оптимизация применяется во многих стандартных библиотеках и игровых движках, но для того времени это был гигантский шаг вперёд. По уровню оптимизации это можно сравнить с тем, как если бы сейчас в «Киберпанк 2077» можно было бы поиграть на простом рабочем компьютере с двухъядерным процессором и встроенной видеокартой.
Чтобы придумать подобное, нужно досконально знать и язык программирования, и то, что нужно оптимизировать. Но в этом есть свой особый кайф: сделать быстрее то, что другие сделать не смогли. Именно благодаря такой оптимизации мы часто можем играть в современные игры не на самом новом железе.
Наоборот это тоже работает: если вы видите игру или программу, которая тормозит на новейшем топовом железе (привет, фотошоп), это значит, что разработчики поленились заняться оптимизацией.























