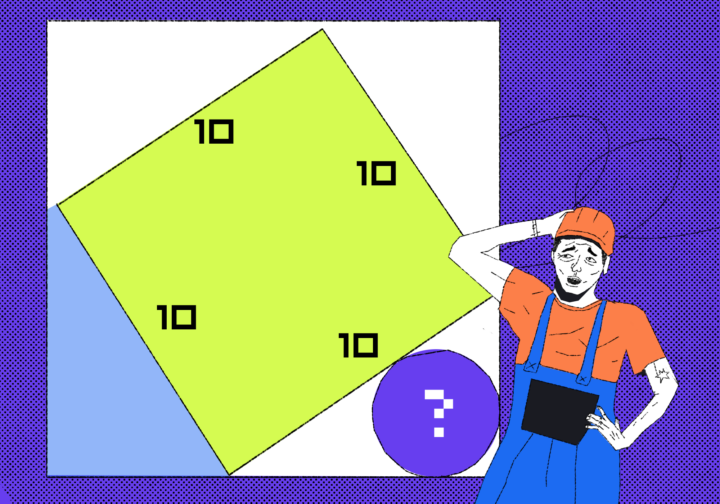
Программист решил у себя на квадратном участке сделать красиво: в центре сделать квадратную песочную зону отдыха, внизу слева — сделать угловую террасу, а справа — выложить плиткой круглую зону под мангал для шашлыков.
Когда он поехал за песком и плиткой, то уже в магазине вспомнил, что забыл записать площадь круга под мангал. Всё, что у него было, — это листок с такой схемой и площадью двух других участков. Но через пару минут программист уже оформлял нужное количество плитки. Как он это сделал?
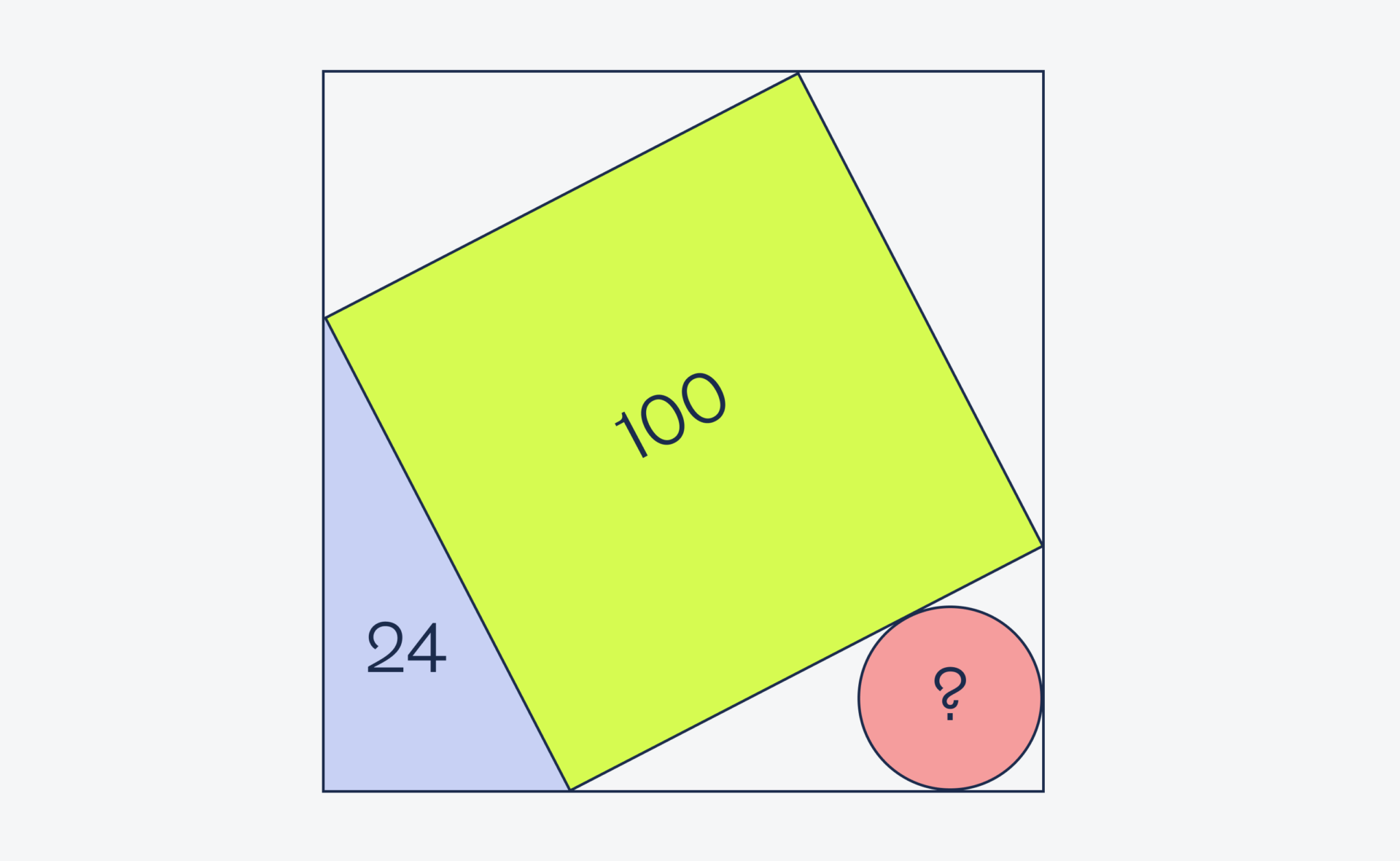
Ключевой момент в этой задаче — это то, что у всех угловых треугольников площадь равна 24. А всё потому, что все эти треугольники — одинаковые. Как бы мы ни вращали один квадрат внутри другого, все угловые треугольники останутся одинаковыми между собой.
Если хотите в этом убедиться более точно — посчитайте противолежащие углы в треугольниках, если значение развёрнутого угла — 180°. А если в треугольниках одинаковые углы и хотя бы одна сторона — это одинаковые треугольники.
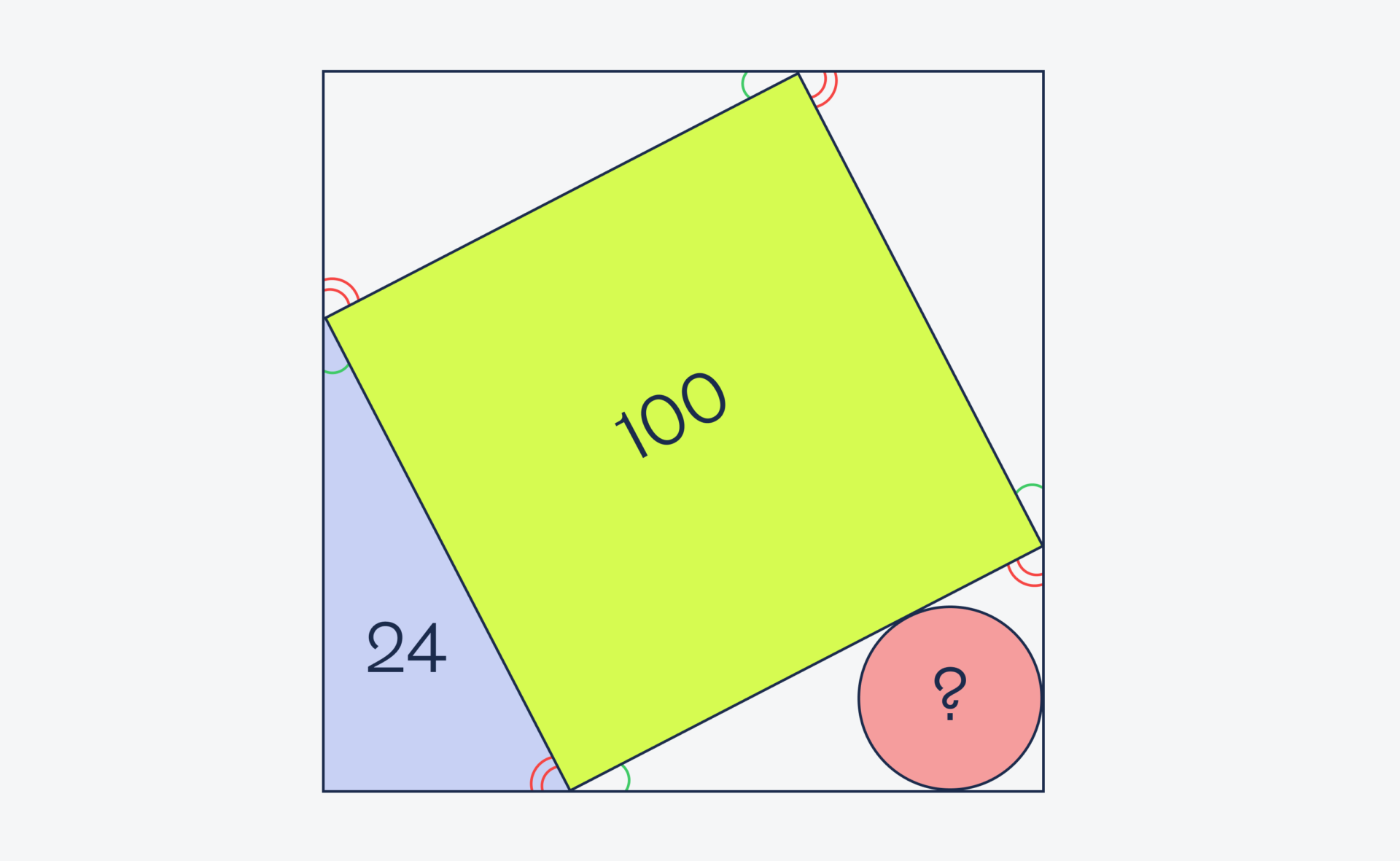
Также сразу посчитаем гипотенузу треугольника — она равна стороне жёлтого квадрата. Раз площадь квадрата равна 100, то сторона равна √100 = 10.
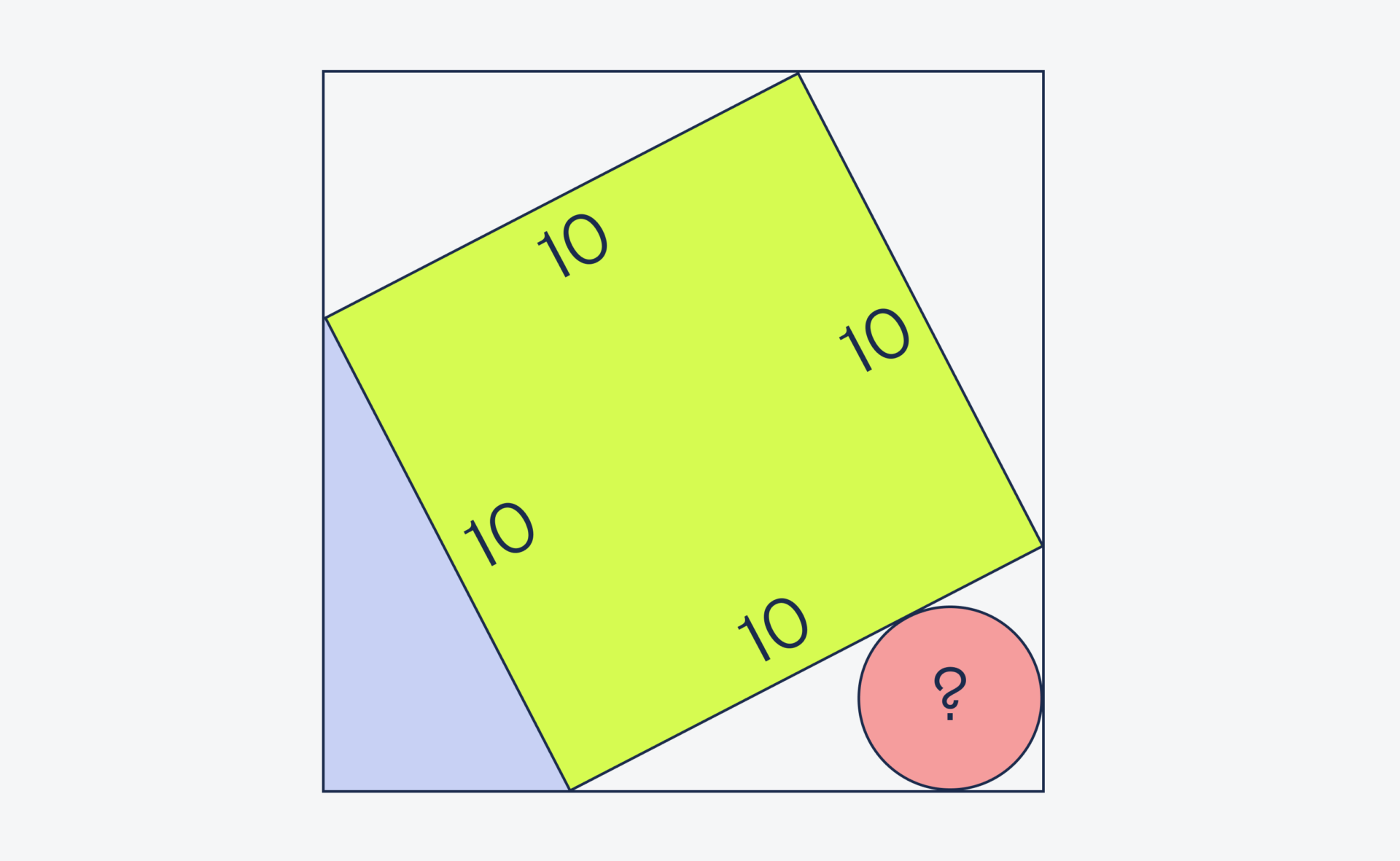
Теперь разберёмся с кругом. У нас получается, что нужно найти площадь окружности, вписанной в прямоугольный треугольник, у которого площадь равна 24, а гипотенуза равна 10.
Для площади круга нам нужно знать его радиус.Призываем на помощь школьную формулу радиуса окружности, вписанной в прямоугольный треугольник:
r = (a + b − c) / 2, где a и b — стороны треугольника, а c — гипотенуза.
Значение гипотенузы мы знаем, найдём длину двух оставшихся сторон. Площадь прямоугольного треугольника равна (a × b) / 2, получается:
(a × b) / 2 = 24 → a × b = 48 → a = 48 / b
Применим теперь формулу из теоремы Пифагора, которая гласит: a² + b² = c², и подставим туда значения a и c:
(48 / b)² + b² = 10²
2304 / b² + b² = 100
Так как у треугольника площадь не равна нулю, это значит, что ни одна из сторон тоже не равна нулю, поэтому умножаем обе части на b², чтобы избавиться от знаменателя:
2304 + b⁴ = 100 × b² → b⁴ − 100 × b² + 2304 = 0
Обозначим b² за x, чтобы получилось обычное квадратное уравнение:
x² − 100 × x + 2304 = 0
Решаем его и получаем, что x = 36 или x = 64. Это значит, что:
b² = 36 → b = 6
b² = 64 → b = 8
А раз a × b = 48, то выходит, что:
a = 48 / 6 = 8
или a = 48 / 8 = 6
Это значит, что стороны треугольника имеют размеры 6, 8 и 10. Подставим это в формулу нахождения радиуса:
r = (a + b − c) / 2 → r = (6 + 8 − 10) / 2 = 2
Теперь считаем площадь круга — это и будет нужное нам число:
S = π × r² → S = π × 4, что примерно равно 12,56.
Получается, программисту нужно взять 13 квадратов плитки. И немного останется на брак и доделки.